Oxygen isotope biogeochemistry of pore water sulfate in the deep ...

More documents

Recommendations

Info

4228 U.G. Wortmann et al. / Geochimica et Cosmochimica Acta 71 (2007) 4221–4232mbsf [m]0255075100125150175200225250275300-50 0 50 100SO 4 [mM] 2-DH 2 S [mM] 2-Dδ 34 S SO 4 [ 0 / 00 ] 2-Dδ 34 S H 2 S [ 0 / 00 ] 2-DΔ 34 S [ 0 / 00 ] 2-DSO 4 [mM] 1-DH 2 S [mM] 1-Dδ 34 S SO 4 [ 0 / 00 ] 1-Dδ 34 S H 2 S [ 0 / 00 ] 1-DΔ 34 S [ 0 / 00 ] 1-DFig. 7. Comparison between the results of a hypothetical 2-Dmodel with a strong horizontal flow component (lines), and theresults of 1-D model which only considers the vertical flowcomponents of the 2-D model (symbols). The largest differences areseen for the concentrations of hydrogen sulfite and sulfate,suggesting that a 1-D model overestimates biological activity inthe presence of a lateral flow component. Note however that thedifferences are small, and that the difference in the isotope data isnegligible. The above results were obtained from models which usesimilar horizontal and vertical scales as observed in the westerntransect of ODP Leg 182 (i.e., Sites 1130 and 1132 Feary et al.,2000a). The models used a fractionation factor of a = 1.07, the 2-Dmodel used horizontal flow velocity of x x = 6.867 · 10 11 m/s, andboth models use a vertical flow velocity of x z = 3.173 · 10 11 m/s,and a sedimentation rate of 7.93 · 10 12 m/s.(Mizutani and Rafter, 1969; Aharon and Fu, 2003). Thefractionation factors for S reported for ODP Site 1130range from 75‰ (direct isotopic difference of dissolved2SO 4and H 2 S) to 65‰ (determined from reaction transportmodeling, Wortmann et al., 2001). We thus use a minimumfractionation factor of 16.25‰, and a maximumfractionation factor of 57‰ to investigate the theoreticald 18 O SO4 2 evolution with depth if it were caused by a kineticisotope effect associated with the volumetric sulfate reductionrate f. Note that the latter fractionation factor ford 18 O SO4 2 is substantially higher than any reported in the literature(up to 21‰, see Böttcher et al., 2005), and we donot imply that those fractionation factors do exist. Wemerely use this number to explore the upper solution envelopeof the model.The volumetric SRR is determined from inverse modelingof the sulfate concentration profile (see, Wortmann,2006). The rates shown in Fig. 8 are higher than those presentedby Wortmann (2006) as the model considers now amajor change in the sedimentation regime during the last20 ky (Hine et al., 2002) which affects the way the upwellingvelocity of the brine is calculated. The calculated SRR isthen used to model the kinetic isotope effect on d 18 O SO4 2 .Fig. 8 shows that a fractionation factor of 16.25‰ is toosmall to explain the observed d 18 O SO4 2 variations. Whilehigher fractionation factors are able to reproduce the peakvalue of d 18 O SO4 2 ¼ 28:6& at 27.5 mbsf, they fail to explainthe values observed in the middle of the profile.Increasing the fractionation factor to values greater than57‰ would solve the discrepancy between 250 and 60 mbsf,but must result in much higher d 18 O SO4 2 values between 60and 0 mbsf (see Fig. 8). An increase of the SRR in the upper30 mbsf, a possibility we cannot exclude, would also increasethe peak for the 16‰ model, but this scenario wouldstill be unable to explain the d 18 O SO4 2 data at 160 mbfs.The only way to explain the observed d 18 O SO4 2 values witha kinetic model would be a variable fractionation factor.However, the required kinetic fractionation factors aremuch higher than those reported in the literature (up to21‰, see Böttcher et al., 2005). We thus conclude that kineticfractionation of oxygen isotopes during microbial sulfatereduction is an unlikely explanation for the ODP Site1130 data.The d 18 O SO4 2 values may be also be influenced by oxygenisotope exchange reactions. Under typical marine conditions,oxygen isotope exchange rates are slow (10 7 years,Chiba and Sakai, 1985). However, metabolic intermediateslike APS or sulfite facilitate oxygen exchange reactions insidethe cytoplasm (Fritz et al., 1989). In this scenario, theoverall oxygen isotope effect depends on the volumetric exchangeflux b, on the completeness of the exchange reaction(k), and the isotopic equilibration fractionation factor .While we have no means to determine k from field measurements,data from ODP Site 1130 clearly shows that at30 mbsf, the isotopic signature of the interstitial water iswithin error similar to the empirical equilibrium constantas determined by Fritz et al. (1989). This implies that thecombination of k and b is large enough to achieve a completeexchange at this depth. We therefore assume thatk = 1, and acknowledge that we may underestimate b.Our model was built without a priory assumptionswhich of the metabolic intermediates facilitates the oxygenisotope exchange, and we are therefore unable to differentiatebetween the individual contributions of APS and sulfite.The measured d 18 O SO4 2 data reaches values of up to 28.6‰,whereas in experiments with sulfur disproportionating bacteriathe oxygen isotope exchange between water and sulfiteand subsequent reoxidation to sulfate typically results inmuch lower values off up to 21‰ at 28 to 35 °C (Böttcheret al., 2001, 2005). Assuming that the oxidation of sulfiteto sulfate adds one oxygen from the cytoplasmic water(d 18 O=0‰), the initial oxygen isotope equilibrium betweensulfite and water in the above experiments wouldhave been close 28.6‰.To achieve the observed d 18 O SO4 2 ¼ 28:6& through theaddition of a water-derived oxygen requires that either theinitial sulfite–water equilibrium was 38.1‰ or that theadded oxygen was enriched relative to the ambient water.In the case of sulfate reducing bacteria, the most likelysource of the oxygen used for the oxidation of sulfite toAPS is adenosine monophosphate (AMP, see Fig. 9).AMP is used in the transformation of sulfite to APS, a reactionthat is reversibly catalyzed by the flavoenzyme APSreductase (Fritz et al., 2002). While we do not know thed 18 O of AMP, its oxygen isotope composition is likely similarto the oxygen isotope equilibrium isotope fractionationbetween inorganic phosphate and water. Following
Oxygen isotope biogeochemistry of pore water sulfate... 4229Measured dataδ 18 O SO4 [ 0 / 00 VSMOV]δ 18 O IW [ 0 / 00 VSMOW]Modeled dataTheoretical δ 18 O SO4 equilibrium [ 0 / 00 VSMOV]δ 18 O SO4 exchange [ 0 / 00 VSMOV]δ 18 O SO4 kinetic α=1.01625 [ 0 / 00 VSMOV]δ 18 O SO4 kinetic α=1.057 [ 0 / 00 VSMOV]Net Flux SO 42Gross Flux SO 4 2- ε=29 0 / 00Gross Flux SO 4 2- ε=50 0 / 00020406080100mbsf1201401601802002202402602803000 10 20 30 40δ 18 O [ 0 / 00 VSMOV]10 -12 10 -11 10 -10mol/m 3 s -1Fig. 8. Oxygen isotope composition of the interstitial water (d 18 O IW ), the d 18 O values from dissolved sulfate (d 18 O SO4 ), as well as the results ofdifferent model runs assuming either a kinetic fractionation ðd 18 O SO4kinetic Þ process or fractionation by isotope exchange reactions d 18 O SO4exchange .The theoretical d 18 O SO4 2 equilibrium values were calculated using the equation of Fritz et al. (1989) from the shipboard temperature data andthe porewater d 18 O measurements.Coleman et al. (2005) and references therein, the oxygenisotopic equilibrium between water and phosphate at 5 °Ccan be calculated as (111.4 5)/4.3 = 24.7. This would implythat the initial sulfite–water equilibrium was 29.9‰,close to the equilibrium constant derived above from thedata reported by Böttcher et al. (2001, 2005).The net flux (i.e., the sulfate reduction rate, SRR) andthe gross flux (i.e., the exchange flux see Fig. 8) is on average14 times higher than the SRR. Similarly high rates arealso reported by Turchyn et al. (2006). These flux rates arehowever critically dependent on the choice of . We thereforealso modeled the case with a considerably higher equilibriumfractionation factor ( =50‰). Such an apparentconstant could result from a combination of an oxygen isotopeexchange effect with a additional kinetic oxygen isotopefractionation (hypothesis C). In this case, therequired volumetric exchange flux b is reduced to the pointthat it becomes smaller than the SRR in the upper 80 mbsf,and is only 4 times higher than the SRR further downcore.However, in the absence of data supporting such highapparent equilibrium constants, we consider a simple exchangemodel the better explanation.The fact that the calculated exchange flux is much greaterthan the flux produced by dissimilatory sulfate reductionposes, however, some difficulties for our understanding of2how SO 4is transported through the cell membrane.While Cypionka (1989) convincingly showed that large2and fast back-fluxes of SO 4across the cell membraneare possible, Brüchert (2004) argues that a large back-fluxwould reduce the membrane potential dW as the sulfateion carries a charge. We note however, that dW dependsnot only on the back-fluxes alone, but on the difference betweenthe sum of the forward and backward fluxes. FurthermoreCypionka (1989) showed that sulfate transportacross the cell membrane can be electroneutral if cell-externalsulfate concentrations are high enough.
Page 1 and 2: Geochimica et Cosmochimica Acta 71
Page 3 and 4: Oxygen isotope biogeochemistry of p
Page 7: Oxygen isotope biogeochemistry of p

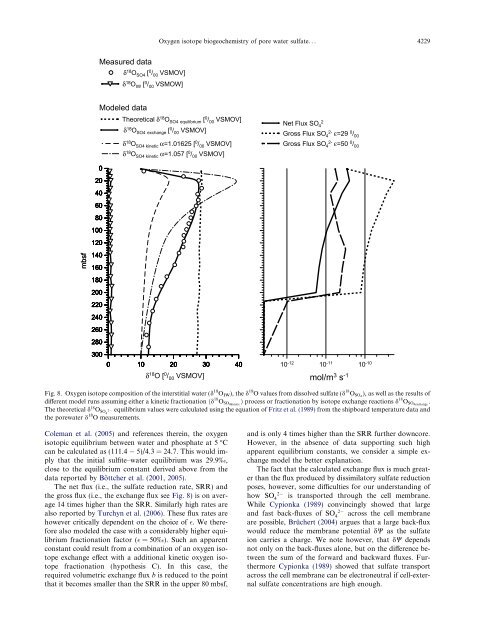
Oxygen isotope biogeochemistry of pore water sulfate in the deep ...

Create successful ePaper yourself

Delete template?

Save as template?