Modeling drawdowns and drawups in financial markets - Risk.net

More documents

Recommendations

Info

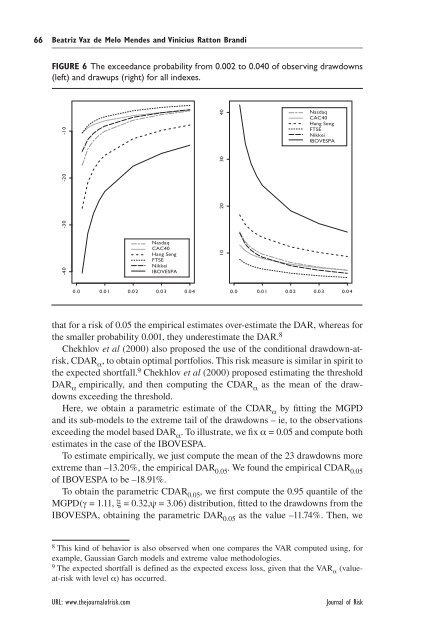
66 Beatriz Vaz de Melo Mendes and Vinicius Ratton Brandi FIGURE 6 The exceedance probability from 0.002 to 0.040 of observing drawdowns (left) and drawups (right) for all indexes. -40 -30 -20 -10 Nasdaq CAC40 Hang Seng FTSE Nikkei IBOVESPA 0.0 0.01 0.02 0.03 0.04 0.0 0.01 0.02 0.03 0.04 that for a risk of 0.05 the empirical estimates over-estimate the DAR, whereas for the smaller probability 0.001, they underestimate the DAR. 8 Chekhlov et al (2000) also proposed the use of the conditional drawdown-atrisk, CDAR α , to obtain optimal portfolios. This risk measure is similar in spirit to the expected shortfall. 9 Chekhlov et al (2000) proposed estimating the threshold DAR α empirically, and then computing the CDAR α as the mean of the drawdowns exceeding the threshold. Here, we obtain a parametric estimate of the CDAR α by fitting the MGPD and its sub-models to the extreme tail of the drawdowns – ie, to the observations exceeding the model based DAR α . To illustrate, we fix α = 0.05 and compute both estimates in the case of the IBOVESPA. To estimate empirically, we just compute the mean of the 23 drawdowns more extreme than –13.20%, the empirical DAR 0.05 . We found the empirical CDAR 0.05 of IBOVESPA to be –18.91%. To obtain the parametric CDAR 0.05 , we first compute the 0.95 quantile of the MGPD(γ = 1.11, ξ = 0.32,ψ = 3.06) distribution, fitted to the drawdowns from the IBOVESPA, obtaining the parametric DAR 0.05 as the value –11.74%. Then, we URL: www.thejournalofrisk.com Journal of Risk 10 20 30 40 Nasdaq CAC40 Hang Seng FTSE Nikkei IBOVESPA 8 This kind of behavior is also observed when one compares the VAR computed using, for example, Gaussian Garch models and extreme value methodologies. 9 The expected shortfall is defined as the expected excess loss, given that the VARα (valueat-risk with level α) has occurred.
Modeling drawdowns and drawups in financial markets 67 collect the 26 observations more extreme than –11.74% and fit the MGPD to the 26 excesses. The best fit was the MGPD(γ = 1, ξ = 0.00,ψ = 6.46). The expected value of this distribution plus the threshold –11.74% yield the final model-based CDAR 0.05 estimate of –18.20%. As noted by Chekhlov et al (2000), solutions from the optimization procedure based on empirical estimation possess high variability, since they are often based on few observations. Using the more accurate estimated values, one may expect to obtain more reliable optimal portfolios based on the minimization of the drawdown-at-risk. We conclude this section by noting that confidence intervals for the parameter estimates, as well as for the DAR α and the CDAR α , can be easily obtained using bootstrap techniques. They will provide, for example, for the DAR α and any α an interval at which this quantity will lie according to some confidence level. 4 Conclusions This paper addresses concerns expressed by traders and investors with respect to the ability of fixed time-scale risk measures to fully characterize risk. Investment risk is perceived differently during periods of consecutive losses, and for many financial series, the total price change over the range of the data is usually concentrated in a few of these strings. The drawdown is a new variable defined over an elastic time scale, and it measures directly the cumulative loss that an investment can incur. We estimated by maximum likelihood the distribution of the severity of drawdowns and drawups from nine stock market indexes, including the three major US indexes and two emerging markets indexes. We showed that the modified generalized Pareto distribution (MGPD) and its sub-models adjust properly to the majority of values previously found to be outliers. Theorems from the extreme value theory supported the use of the MGPD for modeling drawdowns and drawups. Formal statistical tests were carried out to test goodness of fit, confirmed by graphical analysis. The results were compared to the stretched exponential fit. For many data sets, the stretched exponential provided a poor fit for a few extreme observations. In some cases we could also observe the masking effect phenomenon, when the (hidden) largest outlier does not show up at the cost of a poor fit for moderately large observations. For the Nasdaq and the FTSE 100 we noted that, although the cumulative gains tend to be less extreme than the cumulative losses, the sequence of consecutive losses are shorter than the sequences of consecutive gains. The Dow Jones and the S&P500 present drawdowns and drawups with similar duration distributions. However, their drawdowns distributions possess longer tails. The Nikkei 225 presents drawdowns and drawups of similar severity and duration distributions. Consecutive gains from IBOVESPA last longer than consecutive losses and a few may result in extreme cumulative gains. The MGPD parameter estimates indicated that, for most indexes, drawdowns possess heavier tails than drawups, Volume 6/Number 3, Spring 2004 URL: www.thejournalofrisk.com
Page 1 and 2: Modeling drawdowns and drawups in f
Page 9 and 10: TABLE 3 Parameters of maximum likel
Page 13: Modeling drawdowns and drawups in f
Page 17: Modeling drawdowns and drawups in f

Modeling drawdowns and drawups in financial markets - Risk.net

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?