978-1-940366-36-4_WholeBook

Chapter 7 The Condensate of Zero-Point Oscillations and Type-I Superconductors
As a result, we acquire the condition:
1
2 n 0〈∆ 0 〉 = H2 c
8π . (7.12)
This creates a relation of the critical temperature to the critical magnetic field of the
zero-point oscillations condensate of the charged bosons.
5
log E H
Pb
4
In Sn Hg
3
Tl
2
Zn Ga Al
Cd
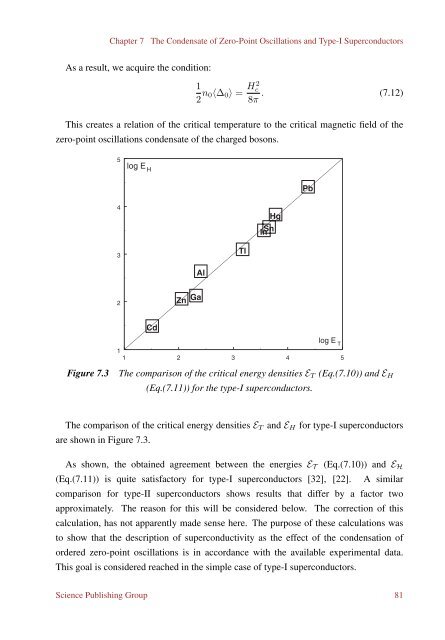
Figure 7.3
log E T
1
1 2 3 4 5
The comparison of the critical energy densities E T (Eq.(7.10)) and E H
(Eq.(7.11)) for the type-I superconductors.
The comparison of the critical energy densities E T and E H for type-I superconductors
are shown in Figure 7.3.
As shown, the obtained agreement between the energies E T (Eq.(7.10)) and E H
(Eq.(7.11)) is quite satisfactory for type-I superconductors [32], [22]. A similar
comparison for type-II superconductors shows results that differ by a factor two
approximately. The reason for this will be considered below. The correction of this
calculation, has not apparently made sense here. The purpose of these calculations was
to show that the description of superconductivity as the effect of the condensation of
ordered zero-point oscillations is in accordance with the available experimental data.
This goal is considered reached in the simple case of type-I superconductors.
Science Publishing Group 81