Contraejemplo de la Conjetura de Aizerman

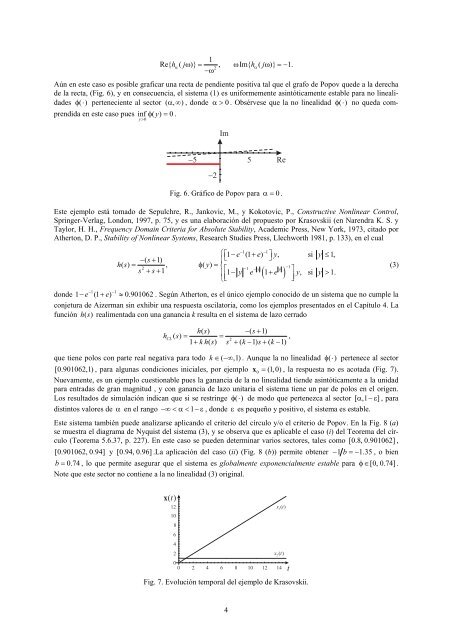
1Re{ hα( jω )} = , ωIm{ h ( j )} 1.2αω =−−ωAún en este caso es posible graficar una recta de pendiente positiva tal que el grafo de Popov quede a la derechade la recta, (Fig. 6), y en consecuencia, el sistema (1) es uniformemente asintóticamente estable para no linealidadesφ( ⋅ ) perteneciente al sector ( α∞ , ) , donde α> 0 . Obsérvese que la no linealidad φ( ⋅ ) no queda comprendidaen este caso pues inf φ ( y) = 0 .y>0Fig. 6. Gráfico de Popov para α= 0 .Este ejemplo está tomado de Sepulchre, R., Jankovic, M., y Kokotovic, P., Constructive Nonlinear Control,Springer-Verlag, London, 1997, p. 75, y es una elaboración del propuesto por Krasovskii (en Narendra K. S. yTaylor, H. H., Frequency Domain Criteria for Absolute Stability, Academic Press, New York, 1973, citado porAtherton, D. P., Stability of Nonlinear Systems, Research Studies Press, Llechworth 1981, p. 133), en el cual⎧⎡ − + ⎤≤hs () , ( )ys + s+ 1 ⎪ 1− y e ( 1 + e ) y, si y > 1.⎩⎣ ⎢⎥ ⎦−1 −11 e (1 e) y, si y 1,− ( s + 1)⎪= φ y = ⎣ ⎦2 ⎨ ⎡ −1−1− y ⎤(3)−1 −1donde 1 − e (1 + e) ≈ 0.901062 . Según Atherton, es el único ejemplo conocido de un sistema que no cumple laconjetura de Aizerman sin exhibir una respuesta oscilatoria, como los ejemplos presentados en el Capítulo 4. Lafunción hs ( ) realimentada con una ganancia k resulta en el sistema de lazo cerradohCLhs () − ( s+1)() s = =21 + kh( s) s + ( k− 1) s+ ( k−1)que tiene polos con parte real negativa para todo k ∈−∞ ( ,1) . Aunque la no linealidad φ( ⋅ ) pertenece al sector[0.901062,1) , para algunas condiciones iniciales, por ejemplo x 0= (1, 0) , la respuesta no es acotada (Fig. 7).Nuevamente, es un ejemplo cuestionable pues la ganancia de la no linealidad tiende asintóticamente a la unidadpara entradas de gran magnitud , y con ganancia de lazo unitaria el sistema tiene un par de polos en el origen.Los resultados de simulación indican que si se restringe φ( ⋅ ) de modo que pertenezca al sector [ α,1 −ε ], paradistintos valores de α en el rango −∞ < α < 1− ε , donde ε es pequeño y positivo, el sistema es estable.Este sistema también puede analizarse aplicando el criterio del círculo y/o el criterio de Popov. En la Fig. 8 (a)se muestra el diagrama de Nyquist del sistema (3), y se observa que es aplicable el caso (i) del Teorema del círculo(Teorema 5.6.37, p. 227). En este caso se pueden determinar varios sectores, tales como [0.8, 0.901062] ,[0.901062, 0.94] y [0.94, 0.96] .La aplicación del caso (ii) (Fig. 8 (b)) permite obtener − 1 b =− 1.35, o bienb = 0.74 , lo que permite asegurar que el sistema es globalmente exponencialmente estable para φ∈ [0, 0.74] .Note que este sector no contiene a la no linealidad (3) original.,Fig. 7. Evolución temporal del ejemplo de Krasovskii.4