Contraejemplo de la Conjetura de Aizerman
Contraejemplo de la Conjetura de Aizerman
Contraejemplo de la Conjetura de Aizerman
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
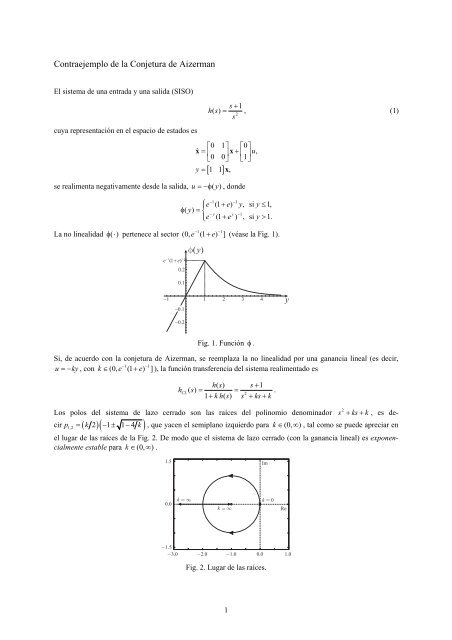
<strong>Contraejemplo</strong> <strong>de</strong> <strong>la</strong> <strong>Conjetura</strong> <strong>de</strong> <strong>Aizerman</strong>El sistema <strong>de</strong> una entrada y una salida (SISO)cuya representación en el espacio <strong>de</strong> estados ess + 1hs () = , (1)2s⎡0 1⎤ ⎡0⎤x= ⎢ x u,0 0⎥ + ⎢1⎥⎣ ⎦ ⎣ ⎦y = 1 1 x,[ ]se realimenta negativamente <strong>de</strong>s<strong>de</strong> <strong>la</strong> salida, u =−φ ( y), don<strong>de</strong>La no linealidad φ( ⋅ ) pertenece al sector−1 −1⎧ ⎪e (1 + e) y, si y ≤1,φ ( y)= ⎨−yy −1⎪⎩ e (1 + e ) , si y > 1.−1 −1(0, e (1 e) ]+ (véase <strong>la</strong> Fig. 1).Fig. 1. Función φ .Si, <strong>de</strong> acuerdo con <strong>la</strong> conjetura <strong>de</strong> <strong>Aizerman</strong>, se reemp<strong>la</strong>za <strong>la</strong> no linealidad por una ganancia lineal (es <strong>de</strong>cir,−1 −1u =− ky, con k∈ (0, e (1 + e) ] ), <strong>la</strong> función transferencia <strong>de</strong>l sistema realimentado eshCLhs () s+1() s = =21 + kh( s)s + ks+ k.Los polos <strong>de</strong>l sistema <strong>de</strong> <strong>la</strong>zo cerrado son <strong>la</strong>s raíces <strong>de</strong>l polinomio <strong>de</strong>nominador s 2 + ks+ k , es <strong>de</strong>cirp1,2 = ( k 2)( − 1± 1− 4 k), que yacen el semip<strong>la</strong>no izquierdo para k ∈(0, ∞ ) , tal como se pue<strong>de</strong> apreciar enel lugar <strong>de</strong> <strong>la</strong>s raíces <strong>de</strong> <strong>la</strong> Fig. 2. De modo que el sistema <strong>de</strong> <strong>la</strong>zo cerrado (con <strong>la</strong> ganancia lineal) es exponencialmenteestable para k ∈(0, ∞ ) .Fig. 2. Lugar <strong>de</strong> <strong>la</strong>s raíces.1
Sin embargo, el sistema con <strong>la</strong> realimentación no lineal u =−φ ( y)x1= x2,x=−φ ( x + x ),2 1 21 1y con condiciones iniciales x 1(0) e −(1 e −1= + ) , x (0) 2= e−1() 2()tiene como solución () x t x tx2 t = e − −, que es mayorque cero para todo t ≥ 0 . Por lo tanto, como x 1() t = x2()t , se observa que x1( t ) crece sin límite para t →∞. Demodo que el sistema con <strong>la</strong> realimentación propuesta no es exponencialmente estable: es inestable (Fig. 3).Fig. 3. (a) Evolución temporal; (b) proyección en el p<strong>la</strong>no x1 − x2.Análisis <strong>de</strong> <strong>la</strong> estabilidad absoluta en base al criterio <strong>de</strong>l círculo y al criterio <strong>de</strong> PopovEn <strong>la</strong> Fig. 4 (a) se muestra el diagrama <strong>de</strong> Nyquist <strong>de</strong>l sistema (1), dibujado para frecuencias positivas. Se observaque no encierra el disco D(a,b); los parámetros a y b <strong>de</strong>ben elegirse <strong>de</strong> modo <strong>de</strong> maximizar <strong>la</strong> amplitud <strong>de</strong>l−1 −1sector que compren<strong>de</strong> <strong>la</strong> no linealidad. Se fijó b en un valor igual a <strong>la</strong> máxima pendiente <strong>de</strong> φ ( b= e (1 + e)),y se <strong>de</strong>terminó a por prueba y error <strong>de</strong> modo que el disco D(a,b) sea casi tangente al diagrama <strong>de</strong> Nyquist. Seencuentra entonces que a = 0.12 . De modo que el criterio <strong>de</strong>l círculo permite <strong>de</strong>terminar que el sistema (1) es−1 −1globalmente exponencialmente estable para cualquier no linealidad comprendida en el sector [0.12, e (1 + e) ] .−1 −1Como <strong>la</strong> no linealidad φ pertenece al sector (0, e (1 + e) ] , el sistema no es estable con esta realimentación.−1 −1Obsérvese que si se elimina el requisito que b= e (1 + e), pue<strong>de</strong>n obtenerse otros sectores, como por ejemplo,los que se muestran en <strong>la</strong> Fig. 4 (b): [0.091,0.18] , [0.18,0.5] y [0.5,4], Esto no significa que el sistema sea globalmenteexponencialmente estable cuando φ pertenece al sector [0.091,4] (<strong>la</strong> unión <strong>de</strong> los tres sectores anteriores,véase Vidyasagar, p. 229).−1 −1Fig. 4: Criterio <strong>de</strong>l círculo para el sistema (1). (a) Sector [0.12, e (1 + e) ] . (b) Tres sectores distintospara el mismo sistema.El comportamiento <strong>de</strong>l sistema también pue<strong>de</strong> analizarse aplicando el criterio <strong>de</strong> Popov. En este caso, el sistemase pue<strong>de</strong> reescribir en <strong>la</strong> forma <strong>de</strong> <strong>la</strong> ecuación 5.6.41−42, p. 230:2
x= Ax+buξ= uy = cx+ dξu =−φ( y)resultandox1= ξ + uξ= uy = x1u =−φ( y)que no es exactamente <strong>la</strong> forma propuesta (obsérvese <strong>la</strong> ecuación <strong>de</strong> x1, que <strong>de</strong>pen<strong>de</strong> <strong>de</strong> ξ y no <strong>de</strong> x1). De modoque <strong>la</strong> matriz A no es Hurwitz, como pi<strong>de</strong> el Teorema 5.6.46 (p. 231) o el Teorema 5.6.63 (p. 233). Para ello,se modifica <strong>la</strong> ecuación <strong>de</strong> x 1, sumando y restando un término <strong>de</strong> <strong>la</strong> forma α x1, con α> 0 , y <strong>de</strong>finiendo unnuevo control v =α x1+ u . Entonces⎧x1 =−α x1+ξ +α x1+ u =−α x1+ξ + v ⎧x1 =−α x1+ξ + v⎪ ξ=−α x1 + v ⎪ ξ=−α x1+ v⎨⇒ ⎨⎪ y = x1 ⎪ y = x1⎪ v [ ( y) x1] ( x1) ⎪⎩ =−φ −α =−ψ ⎩ v =−ψ( x1)Observe que ahora el sistema no presenta <strong>la</strong> integración <strong>de</strong> <strong>la</strong> entrada; <strong>de</strong> hecho, <strong>la</strong> función trasferencia <strong>de</strong>l sistemamodificado ess + 1hα() s =2s +α s+α . (2)También <strong>de</strong>be tenerse presente que si <strong>la</strong> no linealidad φ pertenece al sector ( α, β ) , <strong>la</strong> no linealidad ψ perteneceal sector (0, β −α ) . La i<strong>de</strong>a es analizar el sistema (2) para valores <strong>de</strong>crecientes <strong>de</strong> α , tal que α→ 0 .Para efectuar el gráfico <strong>de</strong> Popov <strong>de</strong>be representarse ωIm{ ha( jω } en función <strong>de</strong> Re{ hα ( jω )} . Es sencillo <strong>de</strong>terminarquey algunos valores particu<strong>la</strong>res son2 4α+ ( α−1)ω −ωRe{ hα( jω )} = , ωIm{ h ( j )} .2 2 2 2 αω =2 2 2 2( α−ω ) +α ω ( α−ω ) +α ω1Re{ hα( jω )} = , ωIm{ h ( )} 0,0 αjω =ω= ω= 0α1Re{ h ( j )} 0, Im{ h ( j )} ,αω α = ωαω α =−ω= ω=1−α1−ααRe{ h ( jω )} = 0, ωIm{ h ( jω )} =−1.αω→∞En <strong>la</strong> Fig. 5 se muestra el gráfico <strong>de</strong> Popov para distintos valores <strong>de</strong> α . Del gráfico se observa que siempre esposible trazar una recta con pendiente positiva, que pase por 1 k = 0 <strong>de</strong> modo que el grafo <strong>de</strong> Popov que<strong>de</strong> a <strong>la</strong><strong>de</strong>recha <strong>de</strong> <strong>la</strong> recta. Esto asegura que el sistema es globalmente asintóticamente estable para una no linealidadψ()⋅ perteneciente al sector (0, k ) = (0, ∞ ) , o bien para φ( ⋅ ) perteneciente al sector ( α∞ , ) .αω→∞Fig. 5. Gráficos <strong>de</strong> Popov para distintos valores <strong>de</strong> α .Finalmente, si α→ 0 , el grafo <strong>de</strong> Popov resulta una semirrecta <strong>de</strong> pendiente cero, ya que para α= 0 ,3
1Re{ hα( jω )} = , ωIm{ h ( j )} 1.2αω =−−ωAún en este caso es posible graficar una recta <strong>de</strong> pendiente positiva tal que el grafo <strong>de</strong> Popov que<strong>de</strong> a <strong>la</strong> <strong>de</strong>recha<strong>de</strong> <strong>la</strong> recta, (Fig. 6), y en consecuencia, el sistema (1) es uniformemente asintóticamente estable para no linealida<strong>de</strong>sφ( ⋅ ) perteneciente al sector ( α∞ , ) , don<strong>de</strong> α> 0 . Obsérvese que <strong>la</strong> no linealidad φ( ⋅ ) no queda comprendidaen este caso pues inf φ ( y) = 0 .y>0Fig. 6. Gráfico <strong>de</strong> Popov para α= 0 .Este ejemplo está tomado <strong>de</strong> Sepulchre, R., Jankovic, M., y Kokotovic, P., Constructive Nonlinear Control,Springer-Ver<strong>la</strong>g, London, 1997, p. 75, y es una e<strong>la</strong>boración <strong>de</strong>l propuesto por Krasovskii (en Narendra K. S. yTaylor, H. H., Frequency Domain Criteria for Absolute Stability, Aca<strong>de</strong>mic Press, New York, 1973, citado porAtherton, D. P., Stability of Nonlinear Systems, Research Studies Press, Llechworth 1981, p. 133), en el cual⎧⎡ − + ⎤≤hs () , ( )ys + s+ 1 ⎪ 1− y e ( 1 + e ) y, si y > 1.⎩⎣ ⎢⎥ ⎦−1 −11 e (1 e) y, si y 1,− ( s + 1)⎪= φ y = ⎣ ⎦2 ⎨ ⎡ −1−1− y ⎤(3)−1 −1don<strong>de</strong> 1 − e (1 + e) ≈ 0.901062 . Según Atherton, es el único ejemplo conocido <strong>de</strong> un sistema que no cumple <strong>la</strong>conjetura <strong>de</strong> <strong>Aizerman</strong> sin exhibir una respuesta osci<strong>la</strong>toria, como los ejemplos presentados en el Capítulo 4. Lafunción hs ( ) realimentada con una ganancia k resulta en el sistema <strong>de</strong> <strong>la</strong>zo cerradohCLhs () − ( s+1)() s = =21 + kh( s) s + ( k− 1) s+ ( k−1)que tiene polos con parte real negativa para todo k ∈−∞ ( ,1) . Aunque <strong>la</strong> no linealidad φ( ⋅ ) pertenece al sector[0.901062,1) , para algunas condiciones iniciales, por ejemplo x 0= (1, 0) , <strong>la</strong> respuesta no es acotada (Fig. 7).Nuevamente, es un ejemplo cuestionable pues <strong>la</strong> ganancia <strong>de</strong> <strong>la</strong> no linealidad tien<strong>de</strong> asintóticamente a <strong>la</strong> unidadpara entradas <strong>de</strong> gran magnitud , y con ganancia <strong>de</strong> <strong>la</strong>zo unitaria el sistema tiene un par <strong>de</strong> polos en el origen.Los resultados <strong>de</strong> simu<strong>la</strong>ción indican que si se restringe φ( ⋅ ) <strong>de</strong> modo que pertenezca al sector [ α,1 −ε ], paradistintos valores <strong>de</strong> α en el rango −∞ < α < 1− ε , don<strong>de</strong> ε es pequeño y positivo, el sistema es estable.Este sistema también pue<strong>de</strong> analizarse aplicando el criterio <strong>de</strong>l círculo y/o el criterio <strong>de</strong> Popov. En <strong>la</strong> Fig. 8 (a)se muestra el diagrama <strong>de</strong> Nyquist <strong>de</strong>l sistema (3), y se observa que es aplicable el caso (i) <strong>de</strong>l Teorema <strong>de</strong>l círculo(Teorema 5.6.37, p. 227). En este caso se pue<strong>de</strong>n <strong>de</strong>terminar varios sectores, tales como [0.8, 0.901062] ,[0.901062, 0.94] y [0.94, 0.96] .La aplicación <strong>de</strong>l caso (ii) (Fig. 8 (b)) permite obtener − 1 b =− 1.35, o bienb = 0.74 , lo que permite asegurar que el sistema es globalmente exponencialmente estable para φ∈ [0, 0.74] .Note que este sector no contiene a <strong>la</strong> no linealidad (3) original.,Fig. 7. Evolución temporal <strong>de</strong>l ejemplo <strong>de</strong> Krasovskii.4
Fig. 8. Criterio <strong>de</strong>l círculo para el ejemplo <strong>de</strong> Krasovskii. (a) Caso i: 0 < a< b. (b) Caso ii: 0 = a < b.El caso (iii) (Fig. 9) también permite <strong>de</strong>terminar distintos sectores tales como [ − 1,0.65] (Fig. 9 (a)) o−1 −1= + pues el disco intersec-[ − 100,0.1] (Fig. 9 (b)). En todos los casos es muy difícil alcanzar el valorta el diagrama <strong>de</strong> Nyquist.b e (1 e)Fig. 9. Criterio <strong>de</strong>l círculo para el ejemplo <strong>de</strong> Krasovskii (Caso iii). (a) φ∈[ − 1,0.65] . (b) φ∈[ − 100,0.1] .Para el análisis <strong>de</strong> estabilidad absoluta también pue<strong>de</strong> aplicarse el criterio <strong>de</strong> Popov (Teorema 5.6.63, p. 233), talcomo se muestra en <strong>la</strong> Fig. 10. En esta figura se muestran dos rectas posibles (a) r = 3, − 1 k =− 1.5 , que aseguraque el sistema es globalmente asintóticamente estable para φ∈ (0, k) = (0,2 3) , y (b) r =∞, − 1 k =− 1.35 , queasegura que el sistema es globalmente asintóticamente estable para φ∈ (0, k) = (0, 0.74) . Obsérvese que en estecaso, no se obtiene una mejor estimación que <strong>la</strong> calcu<strong>la</strong>da con el caso (ii) <strong>de</strong>l criterio <strong>de</strong>l círculo (Fig. 8 (b)).Fig. 10. Criterio <strong>de</strong> Popov para el ejemplo <strong>de</strong> Krasovskii. En este caso, no se obtiene una estimaciónmejor que <strong>la</strong> calcu<strong>la</strong>da don el criterio <strong>de</strong>l círculo (Caso ii, 0 = a < b, Fig. 8 (b)).5