Percolation de premier passage et Coloriages ... - Normalesup.org

il vient
T ( 0, (1 − ε)tλˆx ) ≤ C [(1 − ε)tλ|ˆx| + 1] ≤ t 2 + t 2 = t,
compte tenu de la majoration grossière |ˆx| ≤ 2.
Et si
1
λ ≥ et t ≥ 4CM,
4C(1 − ε)
alors
et
d'après (1.20).
b)
1
(1+ε)t B(t) ⊆ B 0 :
(1 − ε)tλˆx ≥ M,
T ( 0, (1 − ε)tλˆx ) ≤ (1 − ε)t λµ(ˆx) + η (1 − ε)t λ ≤ (1 − ε 2 ) t ≤ t,
} {{ } }{{} }{{}
≤1 mε
≤m −1
x
Soit
(1+ε)t ∈ 1
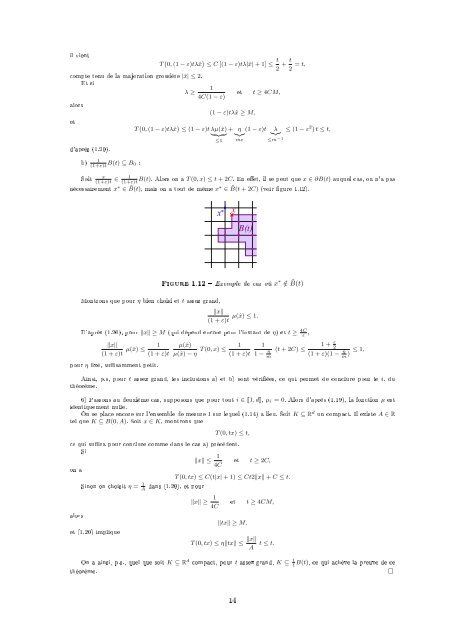
B(t). Alors on a T (0, x) ≤ t + 2C. En eet, il se peut que x ∈ ∂B(t) auquel cas, on n'a pas
(1+ε)t
nécessairement x ∗ ∈ ˜B(t), mais on a tout de même x ∗ ∈ ˜B(t + 2C) (voir gure 1.12).
x*
x
B(t)
Montrons que pour η bien choisi et t assez grand,
Figure 1.12 Exemple de cas où x ∗ /∈ ˜B(t)
‖x‖
µ(ˆx) ≤ 1.
(1 + ε)t
D'après (1.20), pour ‖x‖ ≥ M (qui dépend encore pour l'instant de η) et t ≥ 4C , ε
‖x‖
(1 + ε)t µ(ˆx) ≤ 1
(1 + ε)t
pour η xé, susamment petit.
µ(ˆx)
µ(ˆx) − η T (0, x) ≤ 1
(1 + ε)t
1
1 − η m
(t + 2C) ≤
1 + ε 2
(1 + ε)(1 − η m ) ≤ 1,
Ainsi, p.s, pour t assez grand, les inclusions a) et b) sont vériées, ce qui permet de conclure pour le i. du
théorème.
6) Passons au deuxième cas, supposons que pour tout i ∈ 1, d, µ i = 0. Alors d'après (1.19), la fonction µ est
identiquement nulle.
On se place encore sur l'ensemble de mesure 1 sur lequel (1.14) a lieu. Soit K ⊆ R d un compact. Il existe A ∈ R
tel que K ⊆ B(0, A). Soit x ∈ K, montrons que
T (0, tx) ≤ t,
ce qui sura pour conclure comme dans le cas a) précédent.
Si
on a
alors
Sinon on choisit η = 1 dans (1.20), et pour
A
et (1.20) implique
‖x‖ ≤ 1
4C
et t ≥ 2C,
T (0, tx) ≤ C(t|x| + 1) ≤ Ct2‖x‖ + C ≤ t.
‖x‖ ≥ 1
4C
et
‖tx‖ ≥ M,
t ≥ 4CM,
T (0, tx) ≤ η‖tx‖ ≤ ‖x‖
A t ≤ t.
On a ainsi, p.s., quel que soit K ⊆ R d compact, pour t assez grand, K ⊆ 1 B(t), ce qui achève la preuve de ce
t
théorème.
□
14