Percolation de premier passage et Coloriages ... - Normalesup.org
Percolation de premier passage et Coloriages ... - Normalesup.org
Percolation de premier passage et Coloriages ... - Normalesup.org
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Le <strong>premier</strong> point <strong>de</strong> vue consiste donc à regar<strong>de</strong>r les quantités T (0, u) pour un u ∈ Z d donné (le<br />
point 0 étant l'origine <strong>de</strong> Z d , i.e. (0, 0, . . . , 0)).<br />
Le second consiste à s'intéresser à la zone imprégnée au temps t ∈ R + si le ui<strong>de</strong> part <strong>de</strong> l'origine,<br />
c'est-à-dire à<br />
˜B(t) := { u ∈ Z d | T (0, u) ≤ t } .<br />
Pour simplier les résultats concernant le comportement asymptotique <strong>de</strong> ˜B(t), on introduit<br />
l'ensemble<br />
[<br />
B(t) := ˜B(t) + − 1 2 , 1 d {<br />
= u + (x 1 , x 2 , . . . , x d ) | u ∈<br />
2] ˜B(t) ; ∀i ∈ 1, d, − 1 2 ≤ x i ≤ 1 }<br />
. (1.1)<br />
2<br />
~<br />
B(t)<br />
B(t)<br />
0<br />
On a alors clairement<br />
˜B(t) +<br />
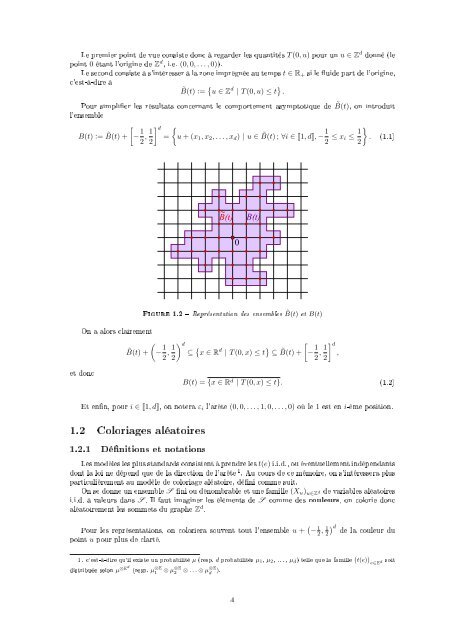
Figure 1.2 Représentation <strong>de</strong>s ensembles ˜B(t) <strong>et</strong> B(t)<br />
(<br />
− 1 2 , 1 2) d<br />
⊆ { x ∈ R d | T (0, x) ≤ t } ⊆ ˜B(t) +<br />
[<br />
− 1 2 , 1 2] d<br />
,<br />
<strong>et</strong> donc<br />
B(t) = {x ∈ R d | T (0, x) ≤ t}. (1.2)<br />
Et enn, pour i ∈ 1, d, on notera ε i l'arête (0, 0, . . . , 1, 0, . . . , 0) où le 1 est en i-ème position.<br />
1.2 <strong>Coloriages</strong> aléatoires<br />
1.2.1 Dénitions <strong>et</strong> notations<br />
Les modèles les plus standards consistent à prendre les t(e) i.i.d., ou éventuellement indépendants<br />
dont la loi ne dépend que <strong>de</strong> la direction <strong>de</strong> l'arête 1 . Au cours <strong>de</strong> ce mémoire, on s'intéressera plus<br />
particulièrement au modèle <strong>de</strong> coloriage aléatoire, déni comme suit.<br />
On se donne un ensemble S ni ou dénombrable <strong>et</strong> une famille (X u ) u∈Z d <strong>de</strong> variables aléatoires<br />
i.i.d. à valeurs dans S . Il faut imaginer les éléments <strong>de</strong> S comme <strong>de</strong>s couleurs, on colorie donc<br />
aléatoirement les somm<strong>et</strong>s du graphe Z d .<br />
Pour les représentations, on coloriera souvent tout l'ensemble u + ( − 1 2 , 1 2) d<br />
<strong>de</strong> la couleur du<br />
point u pour plus <strong>de</strong> clarté.<br />
1. c'est-à-dire qu'il existe un probabilité µ (resp. d probabilités µ 1 , µ 2 , ..., µ d ) telle que la famille ( t(e) ) soit<br />
e∈E<br />
distribuée selon d µ ⊗Ed (resp. µ ⊗E<br />
1 ⊗ µ ⊗E<br />
2 ⊗ . . . ⊗ µ ⊗E<br />
d ). 4