Percolation de premier passage et Coloriages ... - Normalesup.org
Percolation de premier passage et Coloriages ... - Normalesup.org
Percolation de premier passage et Coloriages ... - Normalesup.org
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
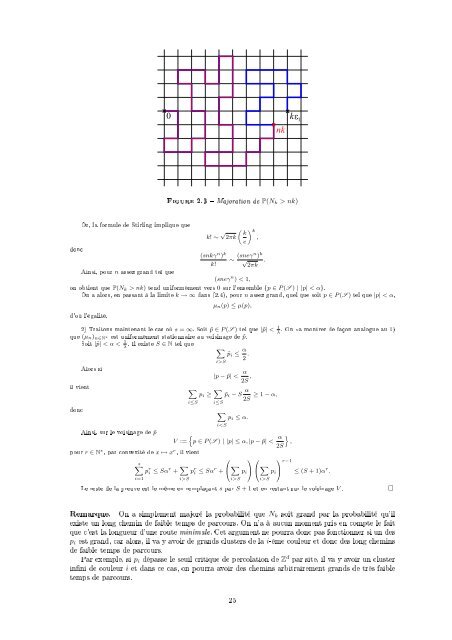
0<br />
nk<br />
k<br />
1<br />
donc<br />
Or, la formule <strong>de</strong> Stirling implique que<br />
Figure 2.3 Majoration <strong>de</strong> P(N k > nk)<br />
k! ∼ √ ( ) k k<br />
2πk ,<br />
e<br />
(snkγ n ) k<br />
k!<br />
∼ (sneγn ) k<br />
√<br />
2πk<br />
.<br />
Ainsi, pour n assez grand tel que<br />
(sneγ n ) < 1,<br />
on obtient que P(N k > nk) tend uniformément vers 0 sur l'ensemble {p ∈ P (S ) | |p| < α}.<br />
On a alors, en passant à la limite k → ∞ dans (2.4), pour n assez grand, quel que soit p ∈ P (S ) tel que |p| < α,<br />
d'où l'égalité.<br />
µ n(p) ≤ µ(p),<br />
2) Traitons maintenant le cas où s = ∞. Soit ˜p ∈ P (S ) tel que |˜p| < 1 . On va montrer <strong>de</strong> façon analogue au 1)<br />
λ<br />
que (µ n ) n∈N ∗ est uniformément stationnaire au voisinage <strong>de</strong> ˜p.<br />
Soit |˜p| < α < 1 . Il existe S ∈ N tel que<br />
λ ∑<br />
il vient<br />
donc<br />
Alors si<br />
Ainsi, sur le voisinage <strong>de</strong> ˜p<br />
pour r ∈ N ∗ , par convexité <strong>de</strong> x ↦→ x r , il vient<br />
s∑<br />
i=1<br />
p r i ≤ Sαr + ∑ i>S<br />
i>S<br />
˜p i ≤ α 2 .<br />
|p − ˜p| < α<br />
2S ,<br />
∑<br />
p i ≥ ∑ ˜p i − S α<br />
2S ≥ 1 − α,<br />
i≤S i≤S<br />
∑<br />
p i ≤ α.<br />
iS i>S<br />
Le reste <strong>de</strong> la preuve est le même en remplaçant s par S + 1 <strong>et</strong> en restant sur le voisinage V .<br />
Remarque. On a simplement majoré la probabilité que N k soit grand par la probabilité qu'il<br />
existe un long chemin <strong>de</strong> faible temps <strong>de</strong> parcours. On n'a à aucun moment pris en compte le fait<br />
que c'est la longueur d'une route minimale. C<strong>et</strong> argument ne pourra donc pas fonctionner si un <strong>de</strong>s<br />
p i est grand, car alors, il va y avoir <strong>de</strong> grands clusters <strong>de</strong> la i-ème couleur <strong>et</strong> donc <strong>de</strong>s long chemins<br />
<strong>de</strong> faible temps <strong>de</strong> parcours.<br />
Par exemple, si p i dépasse le seuil critique <strong>de</strong> percolation <strong>de</strong> Z d par site, il va y avoir un cluster<br />
inni <strong>de</strong> couleur i <strong>et</strong> dans ce cas, on pourra avoir <strong>de</strong>s chemins arbitrairement grands <strong>de</strong> très faible<br />
temps <strong>de</strong> parcours.<br />
25<br />
□