ripartizione forze orizzontali.pdf - Ingegneria Strutturale - Politecnico ...
ripartizione forze orizzontali.pdf - Ingegneria Strutturale - Politecnico ...
ripartizione forze orizzontali.pdf - Ingegneria Strutturale - Politecnico ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
Corso di Strutture Prefabbricate<br />
Distribuzione delle <strong>forze</strong> <strong>orizzontali</strong><br />
dovute a vento o sisma tra setti e pilastri<br />
Marco di Prisco<br />
Dipartimento di <strong>Ingegneria</strong> <strong>Strutturale</strong>, <strong>Politecnico</strong> di Milano
y,v<br />
Ripartizione delle <strong>forze</strong> <strong>orizzontali</strong><br />
Si consideri un generico pannello 2D avente sezione<br />
rettangolare piena, vincolato rigidamente a terra:<br />
H<br />
b<br />
x,u<br />
F<br />
K<br />
x<br />
=<br />
=<br />
h<br />
F x<br />
Ku<br />
K<br />
K<br />
M<br />
M<br />
KV<br />
+ K<br />
V<br />
z,w<br />
u<br />
u<br />
K<br />
K<br />
I<br />
κκκκ =<br />
=<br />
M<br />
xx<br />
M<br />
V<br />
u<br />
=<br />
V<br />
+ u<br />
F<br />
K<br />
x<br />
M<br />
M<br />
; u<br />
V<br />
=<br />
F<br />
K<br />
cEI xx ≅ ; c = 3÷<br />
12<br />
3<br />
H<br />
GA 5<br />
≅ μμμμ<br />
; μμμμ =<br />
H 6<br />
3<br />
bh<br />
= ; A = bh<br />
12<br />
μμμμ GAH<br />
cEI<br />
xx<br />
2<br />
=<br />
( 1<br />
x<br />
V<br />
5<br />
+ νννν )<br />
H<br />
ch<br />
2<br />
2
K<br />
K<br />
K<br />
Trascurando la rigidezza torsionale della<br />
singola parete verticale e quella offerta nei<br />
confronti di uno spostamento ⊥ al piano:<br />
⊥<br />
M<br />
⊥<br />
T<br />
=<br />
⊥<br />
M<br />
⊥<br />
M<br />
K<br />
3<br />
Eb h<br />
= c<br />
12<br />
=<br />
c<br />
K<br />
T<br />
K<br />
+<br />
V<br />
K<br />
V<br />
(b/h)Gb<br />
3<br />
≅<br />
h<br />
K<br />
≤<br />
⊥<br />
M<br />
1<br />
3<br />
Gb<br />
⎛<br />
⎜<br />
K<br />
⎜<br />
⎝<br />
K<br />
3<br />
h<br />
⊥<br />
M<br />
V<br />
=<br />
c(1 + ν) b<br />
6µ H<br />
KT K<br />
÷<br />
2<br />
K<br />
K<br />
2<br />
⊥<br />
⎞<br />
ϕ<br />
T T<br />
V<br />
H<br />
V<br />
T B<br />
α<br />
=<br />
αH<br />
( )<br />
2<br />
2<br />
T<br />
2<br />
3<br />
3<br />
3<br />
T<br />
B<br />
T<br />
h<br />
b<br />
1<br />
c<br />
c<br />
6<br />
)<br />
H<br />
(<br />
H<br />
12<br />
cEbh<br />
H<br />
h<br />
Gb<br />
c<br />
T<br />
T<br />
⎟<br />
⎠<br />
⎞<br />
⎜<br />
⎝<br />
⎛<br />
α<br />
ν<br />
+<br />
=<br />
ϕ<br />
α<br />
ϕ<br />
=
Per la classificazione del sistema di controvento con<br />
sole pareti di taglio si ipotizza K=∞:<br />
a) labile<br />
b) isostatico<br />
c) iperstatico
Nei sistemi isostatici la determinazione delle <strong>forze</strong><br />
agenti su ciascuna parete ricorre al solo equilibrio:<br />
Baricentro delle inerzie dei controventi<br />
1 2<br />
a 1<br />
F y<br />
G I<br />
a 2<br />
K 1 K2<br />
a 2K 2<br />
a 1K 1<br />
R<br />
R<br />
v<br />
v<br />
v<br />
1<br />
1<br />
2<br />
1<br />
2<br />
a<br />
K<br />
2<br />
1<br />
=<br />
=<br />
=<br />
=<br />
=<br />
=<br />
F<br />
F<br />
R<br />
K<br />
2<br />
y<br />
1<br />
1<br />
R<br />
K<br />
v<br />
y<br />
2<br />
2<br />
a<br />
K<br />
1<br />
a<br />
2<br />
1<br />
a<br />
=<br />
1<br />
=<br />
a2<br />
+ a<br />
2<br />
a1<br />
+ a<br />
2<br />
F<br />
a<br />
( a + a )<br />
1<br />
( a + a )<br />
⇒<br />
1<br />
a<br />
2<br />
y<br />
F<br />
y<br />
K<br />
2<br />
2<br />
2<br />
a<br />
2<br />
1<br />
K<br />
=<br />
1<br />
K<br />
2<br />
baricentro delle rigidezze<br />
a<br />
1<br />
K<br />
1
C13 d13 In presenza di 3 pareti non<br />
1<br />
d2 2<br />
3<br />
R2 concorrenti in un punto e non<br />
concorrenti in una retta, si<br />
può usare il metodo di Ritter:<br />
F<br />
Fd<br />
Fd<br />
Fd<br />
13<br />
23<br />
12<br />
=<br />
=<br />
=<br />
R<br />
R<br />
R<br />
2<br />
1<br />
3<br />
d<br />
d<br />
d<br />
2<br />
1<br />
3<br />
R<br />
R<br />
R<br />
2 =<br />
1<br />
3<br />
=<br />
=<br />
d<br />
d<br />
d<br />
d<br />
d<br />
d<br />
13<br />
2<br />
23<br />
1<br />
12<br />
3<br />
F<br />
F<br />
F
Nel caso di controventi disposti ad U spesso si<br />
adottano le relazioni:<br />
C R 1<br />
d c<br />
1<br />
R 3<br />
R R2 d<br />
3<br />
2<br />
F<br />
h<br />
R<br />
1<br />
=<br />
F<br />
Fd<br />
R2<br />
=<br />
h<br />
R = − R<br />
3<br />
Ipotesi: assenza di sforzo di scorrimento<br />
ovvero rigidezza allo scorrimento tra le<br />
pareti 1-3 ed 1-2 nulla.<br />
altrimenti calcolo di d c e profilo soggetto a:<br />
V = F e T = F(d+d c) …. equaz. della torsione mista<br />
2
Sistema iperstatico<br />
Ipotesi<br />
• solai indeformabili nel piano<br />
• controventi perfettamente incastrati alla base<br />
• inerzia costante lungo lo sviluppo longitudinale<br />
dei controventi o variabile con la stessa legge<br />
per tutti i controventi
R 1 R 2 R 3<br />
y<br />
G I<br />
x<br />
xˆ<br />
d<br />
F y<br />
molle in parallelo, con F y posto nel<br />
baricentro delle rigidezze (d=0):<br />
R i<br />
n<br />
k = ∑<br />
i=<br />
1<br />
k<br />
i<br />
R<br />
i<br />
=<br />
k<br />
i<br />
EI<br />
= c<br />
H<br />
k<br />
i<br />
3<br />
i<br />
n<br />
∑ ki<br />
i=<br />
1<br />
F<br />
y<br />
per determinare il baricentro<br />
delle rigidezze:<br />
n<br />
n<br />
∑k<br />
ixi<br />
∑Ii<br />
x<br />
n<br />
i<br />
i=<br />
1<br />
i=<br />
1<br />
Fyx<br />
G = ∑R<br />
ixi<br />
= Fy<br />
= F<br />
I<br />
n y n<br />
i=<br />
1<br />
∑k<br />
i ∑Ii<br />
i=<br />
1<br />
i=<br />
1
Nota la posizione del baricentro delle rigidezze posso<br />
calcolare la generica reazione del controvento i-esimo<br />
che nasce per l’applicazione di una generica forza F y<br />
con d non nullo:<br />
R<br />
i<br />
=<br />
F<br />
y<br />
n<br />
I<br />
∑<br />
i<br />
i=<br />
1<br />
I<br />
i<br />
+<br />
F<br />
y<br />
d<br />
n<br />
xˆ<br />
∑<br />
i=<br />
1<br />
i<br />
I<br />
R i N R i M<br />
Infatti, dall’equilibrio<br />
alla rotazione:<br />
I<br />
i<br />
i<br />
xˆ<br />
2<br />
i<br />
n<br />
F Fy<br />
d =<br />
∑ R Rixˆ<br />
xˆ i = ∑ xˆ xˆ<br />
ϕ<br />
R<br />
G<br />
M<br />
i<br />
=<br />
=<br />
i=<br />
1<br />
n<br />
∑<br />
i=<br />
1<br />
K<br />
F<br />
xˆ<br />
i<br />
y<br />
2<br />
i<br />
ϕ<br />
d<br />
K<br />
G<br />
xˆ<br />
i<br />
i<br />
=<br />
n<br />
i=<br />
1<br />
F<br />
y<br />
d<br />
2<br />
i<br />
ϕ<br />
n<br />
G<br />
xˆ<br />
∑<br />
i=<br />
1<br />
K<br />
i<br />
xˆ<br />
I<br />
i<br />
2<br />
i<br />
i<br />
I<br />
i
0<br />
Presenza di un controvento dominante<br />
R<br />
n<br />
n<br />
y<br />
i<br />
∑<br />
i=<br />
0<br />
∑<br />
i=<br />
1<br />
R<br />
R<br />
x<br />
x<br />
d<br />
= K<br />
i<br />
i<br />
x<br />
= F<br />
i<br />
i<br />
i<br />
y<br />
ϕ<br />
= F<br />
G<br />
y<br />
d<br />
i<br />
F y<br />
eq. traslazione<br />
eq. rotazione<br />
Ipotesi:<br />
I 0>>I i<br />
Il baricentro delle<br />
rigidezze coincide con<br />
l’asse del controvento<br />
dominante
2<br />
i<br />
n<br />
i<br />
i<br />
i<br />
y<br />
2<br />
i<br />
n<br />
i<br />
i<br />
i<br />
y<br />
i<br />
2<br />
i<br />
n<br />
1<br />
i<br />
i<br />
y<br />
G<br />
y<br />
2<br />
i<br />
n<br />
1<br />
i<br />
G<br />
i<br />
i<br />
n<br />
1<br />
i<br />
i<br />
x<br />
I<br />
x<br />
I<br />
d<br />
F<br />
x<br />
K<br />
x<br />
K<br />
d<br />
F<br />
R<br />
x<br />
K<br />
d<br />
F<br />
d<br />
F<br />
x<br />
K<br />
x<br />
R<br />
∑<br />
∑<br />
∑<br />
∑<br />
∑<br />
=<br />
=<br />
=<br />
=<br />
=<br />
=<br />
ϕ<br />
=<br />
ϕ<br />
=<br />
per i=1,n<br />
i<br />
1<br />
i<br />
i<br />
i<br />
1<br />
i<br />
i<br />
x<br />
I<br />
x<br />
K ∑<br />
∑<br />
=<br />
=<br />
si ha inoltre:<br />
⎟<br />
⎟<br />
⎟<br />
⎟<br />
⎟<br />
⎠<br />
⎞<br />
⎜<br />
⎜<br />
⎜<br />
⎜<br />
⎜<br />
⎝<br />
⎛<br />
−<br />
=<br />
+<br />
=<br />
∑<br />
∑<br />
∑<br />
=<br />
=<br />
=<br />
n<br />
1<br />
i<br />
2<br />
i<br />
i<br />
n<br />
1<br />
i<br />
i<br />
i<br />
y<br />
0<br />
n<br />
1<br />
i<br />
i<br />
0<br />
y<br />
x<br />
I<br />
x<br />
I<br />
d<br />
1<br />
F<br />
R<br />
R<br />
R<br />
F
Se I 1 = I 2 = I 3 = I i = ….= I n<br />
R<br />
R<br />
i<br />
0<br />
=<br />
=<br />
F<br />
y<br />
dx<br />
n<br />
∑<br />
i=<br />
1<br />
i<br />
x<br />
2<br />
i<br />
⎛<br />
⎜ d<br />
⎜<br />
Fy<br />
⎜<br />
1−<br />
⎜<br />
⎝ i<br />
n<br />
⎧x<br />
∑ x<br />
i = il<br />
i Se poi, posto l il ⎪<br />
i=<br />
1<br />
n generico interasse: ⎨ 1<br />
2<br />
∑ x xi ⎪⎩ d = nl<br />
i<br />
⎪d = nl<br />
⎩ 2<br />
∑ =1<br />
⎞<br />
⎟<br />
⎟<br />
⎟<br />
⎟<br />
⎠<br />
E ricordando che:<br />
n<br />
∑<br />
i=<br />
1<br />
n<br />
∑<br />
i=<br />
1<br />
i<br />
i<br />
=<br />
2<br />
1<br />
2<br />
=<br />
n<br />
n<br />
( n + 1)<br />
( n + 1)(<br />
2n<br />
+ 1)<br />
6
Le equazioni precedenti divengono:<br />
R<br />
R<br />
i<br />
0<br />
=<br />
1<br />
2<br />
= F<br />
0.50<br />
0.25<br />
( il)<br />
∑ ( il)<br />
y<br />
F<br />
y<br />
n<br />
i=<br />
1<br />
nl<br />
⎡<br />
⎢<br />
⎢1<br />
−<br />
⎢<br />
⎢<br />
⎣<br />
2<br />
nl<br />
2<br />
n<br />
=<br />
∑<br />
∑<br />
= F<br />
⎤ ⎡<br />
il ⎥ ⎢<br />
⎥ = F ⎢<br />
y 1−<br />
⎥ ⎢<br />
⎥ ⎢<br />
⎦ ⎣<br />
2<br />
∑ ( il)<br />
∑ ( i)<br />
i=<br />
1<br />
n<br />
i=<br />
1<br />
2<br />
F<br />
R 0/F y<br />
1<br />
y<br />
n<br />
i=<br />
1<br />
ni<br />
i<br />
2<br />
y<br />
i<br />
2<br />
n<br />
n<br />
2<br />
i=<br />
1<br />
y<br />
( n + 1)(<br />
2n<br />
+ 1)<br />
( n + 1)(<br />
2n<br />
+ 1)<br />
n<br />
∑<br />
i<br />
i=<br />
1<br />
n<br />
2<br />
⎤<br />
⎥<br />
⎥<br />
⎥<br />
⎥<br />
⎦<br />
6n<br />
= F<br />
y<br />
= F i<br />
3<br />
( n + 1)<br />
( )( ) ( ) ⎥ ⎥⎥<br />
⎡ n n ⎤<br />
⎡ ⎤<br />
⎢<br />
⎥ ⎡ 3n<br />
⎤ ⎢ 3<br />
⎢1<br />
− 2 2<br />
⎥ = Fy<br />
⎢1<br />
− ⎥ = Fy<br />
⎢1<br />
−<br />
n n + 1 2n<br />
+ 1<br />
⎢<br />
⎥ ⎣ 2 2n<br />
+ 1 ⎦<br />
2<br />
⎢ 4 +<br />
⎣ 6 ⎦<br />
⎣ n ⎦<br />
n<br />
Per n→∞ R 0/F y → 0.25
Metodo di Capurso<br />
Ipotesi: Ipotesi:<br />
• Ogni singola mensola a profilo aperto viene analizzata utilizzando la<br />
“Teoria delle aree settoriali” di Timoshenko-Vlasov (γ (γzs =0).<br />
• Si trascura la rigidezza fuori piano del generico orizzontamento<br />
• Si considera trascurabile la rigidezza torsionale propria (alla De Saint<br />
Venant) di ogni pannello<br />
• Si trascura il contributo irrigidente delle architravi<br />
T<br />
T<br />
T<br />
B<br />
2<br />
⎛ b ⎞<br />
∝⎜<br />
⎟<br />
⎝ h ⎠<br />
α<br />
≅<br />
0
)<br />
s<br />
(<br />
x<br />
)<br />
z<br />
(<br />
)<br />
z<br />
(<br />
)<br />
z<br />
,<br />
s<br />
(<br />
v<br />
)<br />
s<br />
(<br />
y<br />
)<br />
z<br />
(<br />
)<br />
z<br />
(<br />
)<br />
z<br />
,<br />
s<br />
(<br />
u<br />
⋅<br />
ϑ<br />
+<br />
η<br />
=<br />
⋅<br />
ϑ<br />
−<br />
ξ<br />
=<br />
y, v<br />
ds<br />
dx<br />
)<br />
s<br />
(<br />
y<br />
ds<br />
dy<br />
)<br />
s<br />
(<br />
x<br />
)<br />
s<br />
(<br />
h ⋅<br />
−<br />
⋅<br />
=<br />
α<br />
=<br />
α<br />
=<br />
sin<br />
ds<br />
dy<br />
cos<br />
ds<br />
dx<br />
cos(α-90)= sinα<br />
sin(α-90)= - cosα<br />
ξ(z) x, u<br />
η(z)<br />
θ(z)<br />
ds<br />
)<br />
s<br />
(<br />
y<br />
ds<br />
)<br />
s<br />
(<br />
x<br />
)<br />
s<br />
(<br />
h ⋅<br />
−<br />
⋅<br />
= ds<br />
α<br />
α<br />
α-90
dx( s) dy( s) dx( s) dy( s)<br />
t( s, z) = u( s, z) ⋅ + v( s, z) ⋅ = ξ( z) ⋅ + η( z) ⋅ + ϑ(<br />
z) ⋅h(<br />
s)<br />
ds ds ds ds<br />
γ<br />
dy<br />
h( s)<br />
= x(<br />
s)<br />
⋅ − y(<br />
s)<br />
⋅<br />
ds<br />
zs<br />
dx<br />
ds<br />
u(<br />
s,<br />
z)<br />
= ξ(<br />
z)<br />
−ϑ(<br />
z)<br />
⋅y(<br />
s)<br />
v(<br />
s,<br />
z)<br />
η(<br />
z)<br />
ϑ(<br />
z)<br />
x(<br />
s)<br />
∂ w ( s , z ) ∂ t ( s , z ) ∂ w dx dy<br />
= + = + ξ ' ⋅ + η ' ⋅ + ϑ ' ⋅ h ( s )<br />
∂s<br />
∂z<br />
∂s<br />
ds ds<br />
w( z,<br />
s)<br />
= ζ(<br />
z)<br />
−ξ'<br />
( z)<br />
⋅x(<br />
s)<br />
−η'<br />
( z)<br />
⋅ y(<br />
s)<br />
−ϑ'<br />
( z)<br />
⋅ω(<br />
s)<br />
dω(<br />
s)<br />
=<br />
ds<br />
h(<br />
s)<br />
=<br />
+<br />
⋅<br />
zs = γ<br />
0
)<br />
z<br />
(<br />
),<br />
z<br />
(<br />
),<br />
z<br />
(<br />
),<br />
z<br />
( ϑ<br />
=<br />
ϑ<br />
η<br />
=<br />
η<br />
ξ<br />
=<br />
ξ<br />
ζ<br />
=<br />
ζ<br />
)<br />
s<br />
(<br />
)<br />
z<br />
(<br />
'<br />
'<br />
)<br />
s<br />
(<br />
y<br />
)<br />
z<br />
(<br />
'<br />
'<br />
)<br />
s<br />
(<br />
x<br />
)<br />
z<br />
(<br />
'<br />
'<br />
)<br />
z<br />
(<br />
'<br />
w<br />
)<br />
s<br />
,<br />
z<br />
( ω<br />
⋅<br />
ϑ<br />
−<br />
⋅<br />
η<br />
−<br />
⋅<br />
ξ<br />
−<br />
ζ<br />
=<br />
δ<br />
=<br />
ε<br />
4 funzioni cinematiche incognite<br />
)<br />
s<br />
(<br />
)<br />
z<br />
(<br />
'<br />
'<br />
)<br />
s<br />
(<br />
y<br />
)<br />
z<br />
(<br />
'<br />
'<br />
)<br />
s<br />
(<br />
x<br />
)<br />
z<br />
(<br />
'<br />
'<br />
)<br />
z<br />
(<br />
'<br />
z<br />
w<br />
)<br />
s<br />
,<br />
z<br />
( ω<br />
⋅<br />
ϑ<br />
−<br />
⋅<br />
η<br />
−<br />
⋅<br />
ξ<br />
−<br />
ζ<br />
=<br />
δ<br />
δ<br />
=<br />
ε<br />
( )<br />
ω<br />
⋅<br />
ϑ<br />
−<br />
⋅<br />
η<br />
−<br />
⋅<br />
ξ<br />
−<br />
ζ<br />
⋅<br />
=<br />
σ '<br />
'<br />
y<br />
'<br />
'<br />
x<br />
'<br />
'<br />
'<br />
E
• Dalle ipotesi si ottengono le equazioni di equilibrio:<br />
⎧N<br />
⎪<br />
⎪<br />
⎪M<br />
⎨<br />
⎪M<br />
⎪<br />
⎪<br />
B<br />
⎩<br />
y<br />
x<br />
=<br />
=<br />
=<br />
∫<br />
∫<br />
∫<br />
L<br />
L<br />
L<br />
σ⋅<br />
bds<br />
=<br />
E<br />
σ⋅<br />
x ⋅bds<br />
= E<br />
σ⋅<br />
y⋅<br />
bds = E<br />
( A ⋅ζ'−S<br />
⋅ξ''−S<br />
⋅η'<br />
'−S<br />
⋅ϑ'<br />
')<br />
( S ⋅ζ'−I<br />
⋅ξ''−I<br />
⋅η'<br />
'−I<br />
⋅ϑ'<br />
')<br />
x<br />
xω<br />
( S ⋅ζ'−I<br />
⋅ξ''−I<br />
⋅η'<br />
'−I<br />
⋅ϑ'<br />
')<br />
• Le azioni interne generatrici di tensioni tangenziali<br />
sono:<br />
= ∫<br />
L<br />
σ<br />
⋅ω⋅<br />
bds = E<br />
y<br />
x<br />
xx<br />
yx<br />
dMy<br />
dMx<br />
Vx = Vy<br />
= Mt<br />
dz dz<br />
y<br />
xy<br />
yy<br />
=<br />
dB<br />
dz<br />
ω<br />
y ω<br />
( S ⋅ζ'−I<br />
⋅ξ''−I<br />
⋅η'<br />
'−I<br />
⋅ϑ'<br />
')<br />
ω<br />
ωx<br />
ωy<br />
ωω
• Se N=0 La matrice di rigidezza diventa 3x3<br />
• Definite le:<br />
⎧ξ⎫<br />
⎪ ⎪<br />
= ⎨ η ⎬<br />
⎪ ⎪<br />
⎩ϑ⎭<br />
⎧My<br />
⎫<br />
⎪ ⎪<br />
M<br />
= ⎨ M x ⎬<br />
⎪ ⎪<br />
⎩ B ⎭<br />
⎧V<br />
⎪<br />
= ⎨ V<br />
⎪<br />
⎩M<br />
⎫<br />
⎪<br />
⎬<br />
⎪<br />
⎭<br />
⎧J<br />
⎪<br />
= ⎨ J<br />
⎪<br />
⎩<br />
J<br />
x xx xy xω<br />
δ<br />
V y J yx J yy J y ω<br />
• Le equazioni di equilibrio divengono:<br />
• Le condizioni al contorno per una mensola incastrata<br />
sono:<br />
M = −E<br />
⋅ J⋅<br />
δ''<br />
V = −E<br />
⋅ J⋅<br />
δ'''<br />
δ<br />
ωx<br />
( 0 ) = 0 δ'<br />
( 0)<br />
= 0 δ''<br />
( L)<br />
= 0<br />
t<br />
J<br />
J<br />
J<br />
ωy<br />
J<br />
J<br />
ωω<br />
⎫<br />
⎪<br />
⎬<br />
⎪<br />
⎭
A<br />
S<br />
A<br />
S<br />
y<br />
A<br />
S<br />
x G<br />
x<br />
G<br />
y<br />
G<br />
ω<br />
=<br />
ω<br />
=<br />
=<br />
'<br />
'<br />
'<br />
'<br />
y<br />
'<br />
'<br />
x<br />
' G<br />
G<br />
G<br />
ϑ<br />
⋅<br />
ω<br />
+<br />
η<br />
⋅<br />
+<br />
ξ<br />
⋅<br />
=<br />
ζ<br />
)<br />
'<br />
'<br />
J<br />
'<br />
'<br />
J<br />
'<br />
'<br />
J<br />
(<br />
E<br />
ds<br />
b<br />
x<br />
M x<br />
xy<br />
L<br />
xx<br />
y<br />
ϑ<br />
⋅<br />
+<br />
η<br />
⋅<br />
+<br />
ξ<br />
⋅<br />
⋅<br />
−<br />
=<br />
⋅<br />
⋅<br />
σ<br />
= ω<br />
∫<br />
Se N = 0 Passando al riferimento<br />
baricentrico:<br />
)<br />
'<br />
'<br />
J<br />
'<br />
'<br />
J<br />
'<br />
'<br />
J<br />
(<br />
E<br />
ds<br />
b<br />
B<br />
)<br />
'<br />
'<br />
J<br />
'<br />
'<br />
J<br />
'<br />
'<br />
J<br />
(<br />
E<br />
ds<br />
b<br />
y<br />
M<br />
)<br />
'<br />
'<br />
J<br />
'<br />
'<br />
J<br />
'<br />
'<br />
J<br />
(<br />
E<br />
ds<br />
b<br />
x<br />
M<br />
y<br />
L<br />
x<br />
y<br />
yy<br />
L<br />
xy<br />
x<br />
x<br />
xy<br />
L<br />
xx<br />
y<br />
ϑ<br />
⋅<br />
+<br />
η<br />
⋅<br />
+<br />
ξ<br />
⋅<br />
⋅<br />
−<br />
=<br />
⋅<br />
ω<br />
⋅<br />
σ<br />
=<br />
ϑ<br />
⋅<br />
+<br />
η<br />
⋅<br />
+<br />
ξ<br />
⋅<br />
⋅<br />
−<br />
=<br />
⋅<br />
⋅<br />
σ<br />
=<br />
ϑ<br />
⋅<br />
+<br />
η<br />
⋅<br />
+<br />
ξ<br />
⋅<br />
⋅<br />
−<br />
=<br />
⋅<br />
⋅<br />
σ<br />
=<br />
ωω<br />
ω<br />
ω<br />
ω<br />
ω<br />
∫<br />
∫<br />
∫<br />
G<br />
G<br />
y<br />
y<br />
G<br />
G<br />
x<br />
x<br />
G<br />
G<br />
xy<br />
xy<br />
2<br />
G<br />
2<br />
G<br />
yy<br />
yy<br />
2<br />
G<br />
xx<br />
xx<br />
y<br />
A<br />
I<br />
J<br />
x<br />
A<br />
I<br />
J<br />
y<br />
x<br />
A<br />
I<br />
J<br />
A<br />
I<br />
J<br />
y<br />
A<br />
I<br />
J<br />
x<br />
A<br />
I<br />
J<br />
ω<br />
⋅<br />
⋅<br />
−<br />
=<br />
ω<br />
⋅<br />
⋅<br />
−<br />
=<br />
⋅<br />
⋅<br />
−<br />
=<br />
ω<br />
⋅<br />
−<br />
=<br />
⋅<br />
−<br />
=<br />
⋅<br />
−<br />
=<br />
ω<br />
ω<br />
ω<br />
ω<br />
ωω<br />
ωω
Ripartizione delle azioni <strong>orizzontali</strong><br />
• Per ogni mensola i-esima è possibile scrivere:<br />
Mi i<br />
= −E<br />
⋅ J ⋅ δ''<br />
= −E<br />
⋅ J ⋅ δ'''<br />
Vi i<br />
• In caso di n mensole l’equilibrio dell’intero edificio è:<br />
Mtot = ∑iMi<br />
= −E<br />
⋅ ∑iJi<br />
⋅ δ''<br />
• Ripartizione del momento e del taglio tra le mensole:<br />
i<br />
i<br />
−1<br />
tot<br />
M = J ⋅ J ⋅M<br />
tot<br />
i i '''<br />
J E<br />
Vtot = ∑iVi<br />
= − ⋅ ∑ ⋅ δ<br />
i<br />
i<br />
−1<br />
tot<br />
V = J ⋅ J ⋅<br />
V<br />
tot
Stato di sforzo in ogni mensola<br />
• Solo carico trasversale<br />
• Condizioni al contorno<br />
• Il carico assorbito da ogni mensola<br />
• Risulta quindi<br />
• Le matrici di <strong>ripartizione</strong> sono<br />
V' = −p<br />
V ( L)<br />
= 0<br />
⋅p<br />
M '=<br />
INVARIABILITÀ DELLE MATRICI DI RIPARTIZIONE<br />
p<br />
i<br />
=<br />
J<br />
i<br />
⋅<br />
J<br />
−1<br />
tot<br />
R<br />
i<br />
V<br />
M ( L)<br />
= 0<br />
V '=<br />
−p<br />
=<br />
i<br />
J<br />
i<br />
⋅<br />
J<br />
i<br />
−1<br />
tot
N.B. Teorico solo D.S.V.;<br />
Elementi di guscio:<br />
Nel primo elemento<br />
a= 6m<br />
b= 0.2m<br />
E.F. 0.5x0.5m<br />
∂<br />
2<br />
u<br />
∂y∂z = 0<br />
ϑ [rad]<br />
Altezza [m]
=20 cm<br />
T = 2900kNm χ=0.517<br />
N.B. ε zz, γ xz, γ yz non nulli negli E.F.
σ τ<br />
Sforzi nella sezione di incastro<br />
3 2<br />
t tot<br />
GI ( b ) h<br />
χ<br />
2<br />
=<br />
EI ( b)<br />
ωω
12<br />
y [m]<br />
10<br />
10<br />
z<br />
9<br />
[m]<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
8<br />
6<br />
4<br />
2<br />
0<br />
-2<br />
3<br />
P<br />
C<br />
-4 -2 0 2 4 6<br />
[m]<br />
1<br />
2<br />
x<br />
4t<br />
4m<br />
4t<br />
5m<br />
0<br />
0 0.04 0.08 0.12 0.16<br />
Ux [mm]<br />
0.2<br />
3<br />
2<br />
1<br />
0<br />
0 0.01 0.02 0.03 0.04<br />
30tm<br />
20tm<br />
z<br />
10<br />
[m]<br />
9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
Bugatti, Cavenaghi (2000)<br />
3<br />
2<br />
1<br />
0 0.02 0.04 0.06 0.08 0.1<br />
Uy [mm]<br />
Analitico<br />
Analitico profili sconnessi<br />
Elementi finiti<br />
Capurso [1981]<br />
Analitico = tutte le rigidezze connessione ai piani;<br />
Analitico profili sconnessi = solo rigidezze flessionali<br />
principali; E.F. = rigidezze finite del setto, assiali e<br />
tangenziali dei nuclei controventanti; Capurso = solo<br />
Vlasov ma non D.S.V.; (setti infinit. rigidi ovunque<br />
lungo z)<br />
0<br />
0 0.004 0.008 0.012 0.016 0.02<br />
z<br />
10<br />
[m]<br />
9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
3<br />
2<br />
1<br />
0<br />
-0.02 -0.016 -0.012 -0.008 -0.004 0<br />
0<br />
-0.08 -0.06 -0.04 -0.02<br />
Rz [mrad]<br />
0
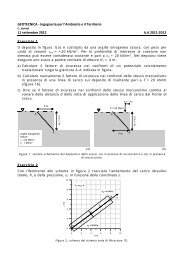
12<br />
y [m]<br />
10<br />
10<br />
h<br />
[m] 9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
8<br />
6<br />
4<br />
2<br />
0<br />
-2<br />
3<br />
P<br />
C<br />
-4 -2 0 2 4 6<br />
[m]<br />
1<br />
2<br />
x<br />
4t<br />
4m<br />
4t<br />
5m<br />
Analitico<br />
Analitico ing. profili sottili<br />
Elementi finiti (gusci)<br />
Elementi finiti (gusci sconnessi)<br />
Elementi finiti a trave<br />
Capurso [1981]<br />
0 0.05 0.1 0.15 0.2 0.25<br />
Ux [mm]<br />
30tm<br />
20tm<br />
h<br />
10<br />
[m] 9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
Bugatti, Cavenaghi (2000)<br />
Analitico<br />
Analitico ing. profili sottili<br />
Elementi finiti (gusci)<br />
Elementi finiti (gusci sconnessi)<br />
Elementi finiti a trave<br />
Capurso [1981]<br />
0 0.02 0.04 0.06 0.08 0.1<br />
Uy [mm]<br />
E.F. a trave = manca la rigidezza di Vlasov<br />
della singola mensola (importante variazione<br />
nella rotazione); E.F. (gusci sconnessi) =<br />
manca la rigidezza di Vlasov del singolo<br />
controvento ed è presente la deformabilità<br />
tangenziale e membranale.<br />
10<br />
h<br />
[m] 9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
Analitico<br />
Analitico ing. profili sottili<br />
Elementi finiti (gusci)<br />
Elementi finiti (gusci sconnessi)<br />
Elementi finiti a trave<br />
Capurso [1981]<br />
-0.08 -0.06 -0.04 -0.02 0<br />
Rz [mrad]
12<br />
y [m]<br />
10<br />
8<br />
6<br />
4<br />
2<br />
0<br />
-2<br />
-4 -2 0 2 4 6<br />
[m]<br />
40<br />
σ [t/m 2 ]<br />
20<br />
0<br />
-20<br />
-40<br />
-60<br />
3<br />
P<br />
C<br />
1<br />
2<br />
x<br />
4t<br />
4m<br />
4t<br />
5m<br />
20tm<br />
Bugatti, Cavenaghi (2000)<br />
Sforzi Sforzi<br />
S<br />
0 1 2 3 4 5 6 7<br />
Ascissa curvilinea [m]<br />
30tm Analitico<br />
Elementi finiti<br />
Capurso [1981]<br />
z=0 m<br />
0<br />
τ [t/m<br />
-2<br />
2 ]<br />
-4<br />
-6<br />
-8<br />
-10<br />
-12<br />
-14<br />
z=2.5 m<br />
0 1 2 3 4 5 6 7<br />
Ascissa curvilinea [m]
12<br />
y [m]<br />
10<br />
Bugatti, Cavenaghi (2000)<br />
Il centro di torsione si sposta: difficoltà di confronto<br />
4t<br />
4m<br />
4t<br />
5m<br />
30tm<br />
20tm<br />
x<br />
C<br />
=<br />
J<br />
ωy<br />
J<br />
xx<br />
8<br />
6<br />
4<br />
2<br />
0<br />
y<br />
C<br />
J<br />
= − ωx<br />
J<br />
yy<br />
Profili sconnessi -2<br />
Profili connessi<br />
-2 0 2 4 6 8<br />
C<br />
C<br />
3<br />
1<br />
2<br />
x [m]<br />
4t<br />
4m<br />
4t<br />
5m<br />
30tm<br />
20tm
Q ~<br />
=<br />
Q ~<br />
0<br />
V S<br />
Q<br />
I<br />
~ 0 c<br />
0 =<br />
α = ωH<br />
= H<br />
w<br />
Φ(<br />
α,<br />
ξ)<br />
h<br />
a<br />
3<br />
Q 0<br />
~<br />
E<br />
3E<br />
c<br />
S<br />
c<br />
A<br />
I<br />
A<br />
h(<br />
I<br />
h<br />
cI<br />
c1<br />
+ I<br />
c2<br />
)
Componenti cinematiche al<br />
variare del n° di gradi di libertà
Edificio<br />
multipiano<br />
H=16.7 m
e = 2.11 m