Elementi di meccanica dei materiali e metallurgia - Matematicamente.it

“Elementi di meccanica dei materiali e metallurgia” di Matteo Puzzle – matematicare@hotmail.com
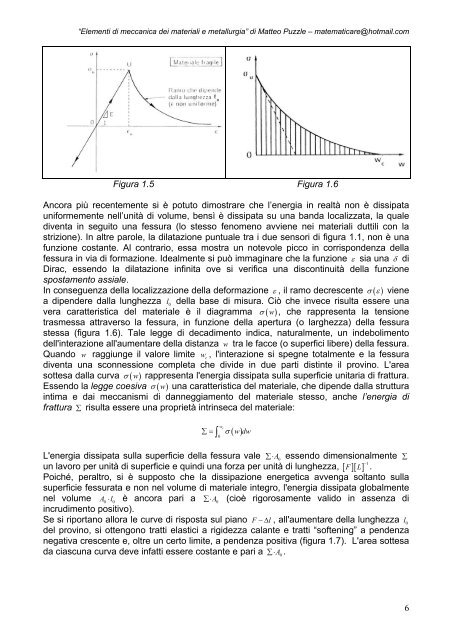
Figura 1.5 Figura 1.6
Ancora più recentemente si è potuto dimostrare che l’energia in realtà non è dissipata
uniformemente nell’unità di volume, bensì è dissipata su una banda localizzata, la quale
diventa in seguito una fessura (lo stesso fenomeno avviene nei materiali duttili con la
strizione). In altre parole, la dilatazione puntuale tra i due sensori di figura 1.1, non è una
funzione costante. Al contrario, essa mostra un notevole picco in corrispondenza della
fessura in via di formazione. Idealmente si può immaginare che la funzione ε sia una δ di
Dirac, essendo la dilatazione infinita ove si verifica una discontinuità della funzione
spostamento assiale.
In conseguenza della localizzazione della deformazione ε , il ramo decrescente σ ( ε ) viene
a dipendere dalla lunghezza l0
della base di misura. Ciò che invece risulta essere una
vera caratteristica del materiale è il diagramma σ ( w)
, che rappresenta la tensione
trasmessa attraverso la fessura, in funzione della apertura (o larghezza) della fessura
stessa (figura 1.6). Tale legge di decadimento indica, naturalmente, un indebolimento
dell'interazione all'aumentare della distanza w tra le facce (o superfici libere) della fessura.
Quando w raggiunge il valore limite wc
, l'interazione si spegne totalmente e la fessura
diventa una sconnessione completa che divide in due parti distinte il provino. L'area
sottesa dalla curva σ ( w)
rappresenta l'energia dissipata sulla superficie unitaria di frattura.
Essendo la legge coesiva σ ( w)
una caratteristica del materiale, che dipende dalla struttura
intima e dai meccanismi di danneggiamento del materiale stesso, anche l’energia di
frattura ∑ risulta essere una proprietà intrinseca del materiale:
∑=∫
wc
0
( )
σ wdw
L'energia dissipata sulla superficie della fessura vale 0 A ∑⋅ essendo dimensionalmente ∑
un lavoro per unità di superficie e quindi una forza per unità di lunghezza, [ ][ ] 1
F L −
.
Poiché, peraltro, si è supposto che la dissipazione energetica avvenga soltanto sulla
superficie fessurata e non nel volume di materiale integro, l'energia dissipata globalmente
nel volume A0⋅ l0
è ancora pari a 0 A ∑⋅ (cioè rigorosamente valido in assenza di
incrudimento positivo).
Se si riportano allora le curve di risposta sul piano F − ∆ l,
all'aumentare della lunghezza l0
del provino, si ottengono tratti elastici a rigidezza calante e tratti “softening” a pendenza
negativa crescente e, oltre un certo limite, a pendenza positiva (figura 1.7). L'area sottesa
da ciascuna curva deve infatti essere costante e pari a ∑⋅ A .
0
6