Elementi di meccanica dei materiali e metallurgia - Matematicamente.it

“Elementi di meccanica dei materiali e metallurgia” di Matteo Puzzle – matematicare@hotmail.com
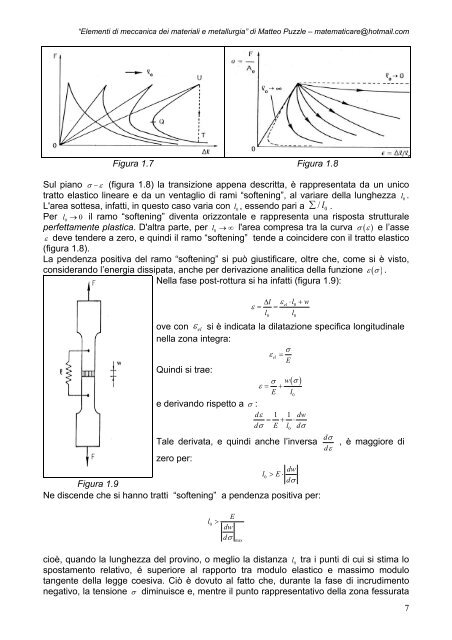
Figura 1.7 Figura 1.8
Sul piano σ − ε (figura 1.8) la transizione appena descritta, è rappresentata da un unico
tratto elastico lineare e da un ventaglio di rami “softening”, al variare della lunghezza l0
.
L'area sottesa, infatti, in questo caso varia con l 0 , essendo pari a ∑ / l0
.
Per l0 → 0 il ramo “softening” diventa orizzontale e rappresenta una risposta strutturale
perfettamente plastica. D'altra parte, per l0 →∞ l'area compresa tra la curva σ ( ε ) e l’asse
ε deve tendere a zero, e quindi il ramo “softening” tende a coincidere con il tratto elastico
(figura 1.8).
La pendenza positiva del ramo “softening” si può giustificare, oltre che, come si è visto,
considerando l’energia dissipata, anche per derivazione analitica della funzione ε ( σ ) .
Nella fase post-rottura si ha infatti (figura 1.9):
∆l
ε
ε = =
l l
0 0
el ⋅ l0+ w
ove con ε el si è indicata la dilatazione specifica longitudinale
nella zona integra:
σ
ε el =
E
Quindi si trae:
σ w(
σ )
e derivando rispetto a σ :
ε = +
E l
dε1 1 dw
= + ⋅
dσE l dσ
Tale derivata, e quindi anche l’inversa
Figura 1.9
dσ
, è maggiore di
dε
zero per:
dw
l0> E⋅ dσ
Ne discende che si hanno tratti “softening” a pendenza positiva per:
l
0
E
>
dw
dσ
cioè, quando la lunghezza del provino, o meglio la distanza l 0 tra i punti di cui si stima lo
spostamento relativo, é superiore al rapporto tra modulo elastico e massimo modulo
tangente della legge coesiva. Ciò è dovuto al fatto che, durante la fase di incrudimento
negativo, la tensione σ diminuisce e, mentre il punto rappresentativo della zona fessurata
max
0
0
7