mekanik I, 080526-1 Frilägg kranarmen! Den påverkas av ...
mekanik I, 080526-1 Frilägg kranarmen! Den påverkas av ...
mekanik I, 080526-1 Frilägg kranarmen! Den påverkas av ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
x<br />
z<br />
<br />
4a<br />
A<br />
P<br />
B<br />
E<br />
C<br />
(0,4,6) a<br />
S<br />
(-3,10,0) a<br />
y<br />
D<br />
<strong>mekanik</strong> I, <strong>080526</strong>-1<br />
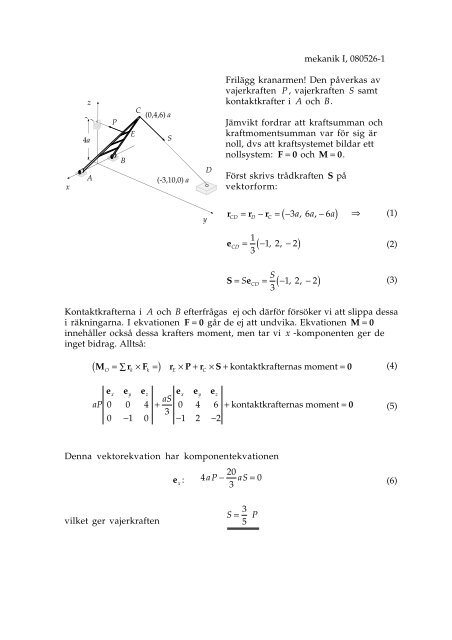
<strong>Frilägg</strong> <strong>kranarmen</strong>! <strong>Den</strong> <strong>påverkas</strong> <strong>av</strong><br />
vajerkraften P , vajerkraften S samt<br />
kontaktkrafter i A och B.<br />
Jämvikt fordrar att kraftsumman och<br />
kraftmomentsumman var för sig är<br />
noll, dvs att kraftsystemet bildar ett<br />
nollsystem: F = 0 och M = 0.<br />
Först skrivs trådkraften S på<br />
vektorform:<br />
( )<br />
rCD = rD− rC=<br />
−3a, 6a, −6a<br />
e CD<br />
1<br />
= −1, 2, −2<br />
3<br />
( )<br />
⇒ (1)<br />
(2)<br />
S<br />
S= SeCD<br />
= ( −1, 2, −2)<br />
(3)<br />
3<br />
Kontaktkrafterna i A och B efterfrågas ej och därför försöker vi att slippa dessa<br />
i räkningarna. I ekvationen F = 0 går de ej att undvika. Ekvationen M = 0<br />
innehåller också dessa krafters moment, men tar vi x -komponenten ger de<br />
inget bidrag. Alltså:<br />
( ) × + × + =<br />
M = ∑ r × F = r P r S kontaktkrafternas moment 0 (4)<br />
aP<br />
O k k E C<br />
ex ey ez ex ey ez<br />
aS<br />
0 0 4 + 0 4 6<br />
3<br />
0 −1<br />
0 −1 2 −2<br />
<strong>Den</strong>na vektorekvation har komponentekvationen<br />
vilket ger vajerkraften<br />
e x :<br />
+ kontaktkrafternas moment =<br />
0<br />
(5)<br />
4<br />
20<br />
aP− aS=<br />
0<br />
3<br />
(6)<br />
S P<br />
= 3<br />
5
l<br />
f<br />
d<br />
N<br />
mg<br />
mg<br />
N<br />
mg<br />
<strong>mekanik</strong> I, <strong>080526</strong>-2<br />
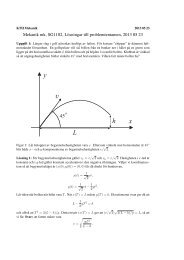
Kroppen <strong>påverkas</strong> <strong>av</strong> tyngdkraften mg,<br />
normalkraften N samt friktionskraften<br />
f . Vi söker i princip minsta begynnelseenergi<br />
i fjädern för att föra upp kroppen<br />
till översta läget utan att den förlorar<br />
kontakten med banan. Vilkoret är då att<br />
normalkraften är noll i det översta läget.<br />
Om bara tyngdkraften verkar i det<br />
översta läget säger kraftekvationens<br />
vertikala komponent att<br />
v<br />
m<br />
r<br />
<strong>Den</strong> minsta fart kroppen kan ha i översta läget är alltså<br />
2<br />
1<br />
= mg<br />
(1)<br />
v1 = gr.<br />
1 2<br />
Kroppen är från början i vila. Fjäderkraften gör arbetet kl . Det är ett positivt<br />
2<br />
arbete så att kroppens kinetiska energi ökar medan tyngdkraftens arbete<br />
−mg ⋅2<br />
r och friktionskraftens arbete −µmg ⋅d<br />
är negativa. Summan <strong>av</strong> alla<br />
arbeten skall ge kinetisk energi i det översta läget.<br />
Lagen arbetet:<br />
Sätt i ekv (1)!<br />
<strong>Den</strong> minsta fjäderförkortningen är<br />
U = T −T<br />
1 0 (2)<br />
1 2<br />
1 2<br />
k l −µ mg ⋅d−mg ⋅ 2r<br />
= mv1<br />
−0<br />
(3)<br />
2<br />
2<br />
2<br />
k l = 5mgr + 2µ<br />
mgd<br />
(4)<br />
l =<br />
( )<br />
mg 5r+ 2µ<br />
d<br />
k
a<br />
B<br />
A<br />
v 0<br />
l<br />
mv 1<br />
β β<br />
C mv 0<br />
I<br />
<strong>mekanik</strong> I, <strong>080526</strong>-3<br />
Figuren visar att när pucken kommer till C är rörelsemängden mv0 . I detta<br />
läge blir tråden sträckt och en trådkraft uppkommer plötsligt. Under ett kort<br />
tidsintervall ger trådkraften en impuls, som ändrar rörelsemängden till mv1 vinkelrätt mot tråden. Bankurvan är en cirkelrörelse efteråt. Impulsen måste<br />
ju vara i trådens riktning och därför ges impulsen <strong>av</strong> triangelgeometrin<br />
Impulslagen:<br />
I= mv −mv<br />
1 0 (1)<br />
är en vektorekvation. Impulsens storlek ges alltså enligt figuren <strong>av</strong><br />
I = mv ⋅cosβ<br />
(2)<br />
Avståndet mellan B och C bestäms med Pythagoras sats och då kan cosβ<br />
skrivas:<br />
Insättning i ekv (2) ger<br />
<strong>Den</strong> maximala farten blir då<br />
0<br />
cosβ =<br />
I = mv<br />
Insättning <strong>av</strong> numeriska värden ger<br />
v<br />
0<br />
l − a<br />
l<br />
2 2<br />
l − a<br />
l<br />
2 2<br />
l<br />
=<br />
m l − a<br />
0 2 2<br />
I<br />
v 32 .<br />
0 = m/s = 2.0 m/s<br />
20 . 064 .<br />
(3)<br />
(4)
θ<br />
<br />
<br />
kbθ<br />
c<br />
b<br />
För att eliminera reaktionskraften i O ställer vi upp<br />
momentekvationen<br />
som allmänt har z-komponenten<br />
O<br />
<strong>mekanik</strong> I, <strong>080526</strong>-4<br />
Svängningstiden för stångens små<br />
svängningar kring det horisontella<br />
jämviktsläget skall bestämmas. Låt<br />
vinkeln θ vara stångens vridningsvinkel,<br />
som alltså är liten. Fjäderns<br />
förlängning räknat från jämviktsläget<br />
är då bθ . Massans hastighet är c ˙ θ .<br />
<strong>Frilägg</strong> kroppen! <strong>Den</strong> <strong>påverkas</strong> <strong>av</strong><br />
tyngdkraften, fjäderkraften och reaktionskraften<br />
vid O. I jämviktsläget<br />
balanseras tyngdkraftens moment<br />
med <strong>av</strong>seende på O <strong>av</strong> fjäderkraftens<br />
moment. Dessa statiska krafter kan<br />
man alltså bortse ifrån i det dynamiska<br />
fallet.<br />
M = H˙<br />
(1)<br />
O O<br />
M = H˙<br />
(2)<br />
z z<br />
<strong>Den</strong> enda dynamiska kraft som ger moment är fjäderkraftens dynamiska del<br />
kbθ . Rörelsemängdsmomentet för plan rörelse i planpolära koordinater är<br />
mc 2 θ ˙ . Alternativt bestäms det som hävarm gånger rörelsemängd c⋅mcθ ˙ .<br />
Insättning i momentekvationen ger<br />
Standardekvationen blir<br />
− ⋅ = d<br />
b kbθ<br />
( θ)<br />
Identifiering ger då egenvinkelfrekvensen i kvadrat<br />
Perioden är då<br />
t mc<br />
2 ˙<br />
d<br />
(3)<br />
2<br />
mc ˙˙ 2<br />
θ + k b θ = 0<br />
(4)<br />
2<br />
˙˙ kb<br />
θ + θ = 0 (5)<br />
2<br />
mc<br />
ω 2<br />
n<br />
2<br />
kb<br />
= (6)<br />
2<br />
mc<br />
c<br />
τn= 2π<br />
b<br />
m<br />
k