Geometrie pro FST 2
Geometrie pro FST 2
Geometrie pro FST 2
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>Geometrie</strong> <strong>pro</strong> <strong>FST</strong> 2<br />
Pomocný učební text<br />
František Ježek, Světlana Tomiczková<br />
Plzeň, 28. srpna 2013, verze 6.0
Předmluva<br />
Tento pomocný text vznikl <strong>pro</strong> potřeby předmětu <strong>Geometrie</strong> <strong>pro</strong> <strong>FST</strong> 2, který vyučujeme<br />
<strong>pro</strong> studenty druhého ročníku Strojní fakulty v zimním semetru. Snažili jsme se napsat<br />
velice stručné a jednoduché pojednání. Věříme, že je to ta forma, kterou studenti potřebují.<br />
Pokud jsme v textu nechali nedopatření, resp. pokud je text někde nesrozumitelný,<br />
<strong>pro</strong>síme o sdělení takových poznatků. Ideální cestou <strong>pro</strong> takové sdělení je použití e-mailu<br />
a adresy JEZEK@KMA.ZCU.CZ. Zvláště pilní hledači chyb a překlepů budou odměněni.<br />
Věříme, že tou odměnou ale bude především úspěšné složení zkoušky, nebot’ ten, kdo<br />
našel chybu, zpravidla přemýšlel. Právě geometrie je příležitostí k ověření myšlenkového<br />
potenciálu.<br />
Autoři<br />
2
Obsah<br />
1 Geometrická zobrazení a transformace souřadnic 6<br />
1.1 Transformace kartézského systému souřadnic . . . . . . . . . . . . . . . . . 7<br />
1.2 Homogenní souřadnice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10<br />
1.3 Geometrické transformace v E 2 , resp. v P (E 2 ) . . . . . . . . . . . . . . . . 10<br />
1.3.1 Posunutí neboli translace . . . . . . . . . . . . . . . . . . . . . . . . 10<br />
1.3.2 Otáčení neboli rotace okolo bodu . . . . . . . . . . . . . . . . . . . 11<br />
1.3.3 Osová souměrnost . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11<br />
1.3.4 Změna měřítka neboli dilatace . . . . . . . . . . . . . . . . . . . . . 12<br />
1.3.5 Obecná afinní transformace . . . . . . . . . . . . . . . . . . . . . . 12<br />
1.3.6 Skládání transformací . . . . . . . . . . . . . . . . . . . . . . . . . 13<br />
1.3.7 Inverzní geometrická transformace . . . . . . . . . . . . . . . . . . . 13<br />
1.4 Geometrické transformace v E 3 , resp. v P (E 3 ) . . . . . . . . . . . . . . . . 14<br />
1.4.1 Posunutí neboli translace . . . . . . . . . . . . . . . . . . . . . . . . 14<br />
1.4.2 Otáčení neboli rotace okolo osy . . . . . . . . . . . . . . . . . . . . 14<br />
1.4.3 Souměrnost podle roviny . . . . . . . . . . . . . . . . . . . . . . . . 15<br />
1.4.4 Dilatace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15<br />
1.4.5 Obecná afinní transformace a <strong>pro</strong>jektivní transformace . . . . . . . 15<br />
1.5 Skládání transformací a inverzní transformace . . . . . . . . . . . . . . . . 16<br />
1.6 Cvičení . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17<br />
1.7 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19<br />
2 Křivky 20<br />
2.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20<br />
2.1.1 Tečna a normála křivky . . . . . . . . . . . . . . . . . . . . . . . . 21<br />
2.1.2 Klasifikace bodů křivky . . . . . . . . . . . . . . . . . . . . . . . . . 22<br />
2.1.3 Rektifikace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22<br />
2.1.4 Oskulační rovina a oskulační kružnice . . . . . . . . . . . . . . . . . 23<br />
2.1.5 Obálka . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25<br />
2.1.6 Ekvidistanta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26<br />
2.1.7 Cykloida . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26<br />
2.1.8 Evoluta a evolventa . . . . . . . . . . . . . . . . . . . . . . . . . . . 26<br />
2.1.9 Řídící kuželová plocha . . . . . . . . . . . . . . . . . . . . . . . . . 26<br />
2.2 Šroubovice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27<br />
2.2.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27<br />
2.2.2 Parametrické vyjádření šroubovice . . . . . . . . . . . . . . . . . . 27<br />
3
OBSAH 4<br />
2.2.3 Tečna šroubovice a její průvodní trojhran . . . . . . . . . . . . . . . 28<br />
2.2.4 Křivosti šroubovice . . . . . . . . . . . . . . . . . . . . . . . . . . . 29<br />
2.3 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32<br />
3 Obecné poznatky o plochách 33<br />
3.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33<br />
3.2 Úlohy na plochách . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35<br />
3.3 Výpočetní řešení některých úloh na plochách . . . . . . . . . . . . . . . . . 37<br />
3.4 Gaussova křivost plochy . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38<br />
3.5 Parametrické vyjádření ploch . . . . . . . . . . . . . . . . . . . . . . . . . 38<br />
3.6 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40<br />
4 Rotační plochy 41<br />
4.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41<br />
4.2 Parametrické vyjádření rotační plochy . . . . . . . . . . . . . . . . . . . . 42<br />
4.3 Vlastnosti rotačních ploch . . . . . . . . . . . . . . . . . . . . . . . . . . . 43<br />
4.4 Klasifikace rotačních ploch . . . . . . . . . . . . . . . . . . . . . . . . . . . 44<br />
4.5 Úlohy na rotačních plochách . . . . . . . . . . . . . . . . . . . . . . . . . . 44<br />
4.6 Průniky rotačních ploch . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47<br />
4.7 Rotační kvadriky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47<br />
4.8 Cvičení . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48<br />
4.9 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49<br />
5 Šroubové plochy 50<br />
5.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50<br />
5.2 Parametrické vyjádření šroubové plochy . . . . . . . . . . . . . . . . . . . 50<br />
5.3 Vlastnosti šroubových ploch . . . . . . . . . . . . . . . . . . . . . . . . . . 51<br />
5.4 Klasifikace šroubových ploch . . . . . . . . . . . . . . . . . . . . . . . . . . 52<br />
5.5 Úlohy na šroubových plochách . . . . . . . . . . . . . . . . . . . . . . . . . 52<br />
5.6 Cvičení . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54<br />
5.7 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54<br />
6 Obalové plochy 56<br />
6.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56<br />
6.2 Charakteristika roviny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57<br />
6.3 Charakteristika kulové plochy . . . . . . . . . . . . . . . . . . . . . . . . . 59<br />
6.4 Metoda kulových ploch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61<br />
6.5 Metoda tečných rovin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63<br />
6.6 Určení obalové plochy výpočtem . . . . . . . . . . . . . . . . . . . . . . . . 65<br />
6.7 Cvičení . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67<br />
6.8 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67<br />
7 Rozvinutelné plochy 68<br />
7.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68<br />
7.2 Typy rozvinutelných ploch . . . . . . . . . . . . . . . . . . . . . . . . . . . 68<br />
7.3 Metody komplanace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
OBSAH 5<br />
7.3.1 Metoda normálového řezu . . . . . . . . . . . . . . . . . . . . . . . 69<br />
7.3.2 Metoda triangulace . . . . . . . . . . . . . . . . . . . . . . . . . . . 70<br />
7.4 Tečna křivky v rozvinutí . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71<br />
7.5 Rozvinutí rozvinutelné šroubové plochy . . . . . . . . . . . . . . . . . . . . 71<br />
7.6 Konstrukce a rozvinutí přechodové rozvinutelné plochy . . . . . . . . . . . 72<br />
7.7 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73<br />
8 Některé nekartézské souřadnicové soustavy 74<br />
8.1 Sférické souřadnice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74<br />
8.2 Cylindrické souřadnice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74<br />
8.3 Využití nekartézských souřadnic . . . . . . . . . . . . . . . . . . . . . . . . 75<br />
8.4 Cvičení . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75<br />
8.5 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76<br />
9 Nelineární útvary v rovině a v <strong>pro</strong>storu 77<br />
9.1 Vyjádření křivek . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77<br />
9.1.1 Kružnice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77<br />
9.1.2 Elipsa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79<br />
9.1.3 Parabola . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80<br />
9.1.4 Hyperbola . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81<br />
9.1.5 Obecná rovnice kuželosečky . . . . . . . . . . . . . . . . . . . . . . 81<br />
9.2 Vektorové vyjádření kuželových a válcových ploch . . . . . . . . . . . . . . 86<br />
9.2.1 Obecná kuželová plocha . . . . . . . . . . . . . . . . . . . . . . . . 86<br />
9.2.2 Obecná válcová plocha . . . . . . . . . . . . . . . . . . . . . . . . . 86<br />
9.3 Rotační plochy druhého stupně (kvadriky) v E 3 . . . . . . . . . . . . . . . 87<br />
9.3.1 Kulová plocha . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87<br />
9.3.2 Rotační elipsoid . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87<br />
9.3.3 Rotační paraboloid . . . . . . . . . . . . . . . . . . . . . . . . . . . 87<br />
9.3.4 Rotační hyperboloid jednodílný . . . . . . . . . . . . . . . . . . . . 88<br />
9.3.5 Rotační hyperboloid dvoudílný . . . . . . . . . . . . . . . . . . . . 88<br />
9.4 Obecná rovnice kvadriky . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88<br />
9.5 Kuželosečky a kvadriky v obecné poloze . . . . . . . . . . . . . . . . . . . 97<br />
9.6 Cvičení . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99<br />
9.7 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
Kapitola 1<br />
Geometrická zobrazení<br />
a transformace souřadnic<br />
Uvažujme dvě množiny bodů M a N. Geometrickým zobrazením T rozumíme předpis,<br />
kterým každému bodu X (vzoru) z množiny M přiřadíme jednoznačně bod T(X) (obraz)<br />
z množiny N. Příkladem geometrického zobrazení je kolmé <strong>pro</strong>mítání do půdorysny (roviny<br />
xy), posunutí o daný vektor, otočení okolo dané osy apod.<br />
Řekneme, že geometrické zobrazení T je vzájemně jednoznačné, jestliže každým dvěma<br />
různým bodům jsou přiřazeny různé body, tj. platí-li<br />
X ≠ Y, X ∈ M, Y ∈ M ⇒ T(X) ≠ T(Y ) .<br />
Pro vzájemně jednoznačné zobrazení T množiny M na množinu N, tj. <strong>pro</strong> <strong>pro</strong>sté zobrazení,<br />
existuje zobrazení T −1 , které obrazu Y = T(X) přiřadí vzor, tj. bod X. Říkáme, že<br />
zobrazení T −1 je inverzní k zobrazení T.<br />
Vzájemně jednoznačné zobrazení, <strong>pro</strong> nějž M = N, nazýváme transformace. Např.<br />
<strong>pro</strong> posunutí můžeme položit M = N = E 3 a jistě jde o <strong>pro</strong>sté zobrazení, tj. posunutí<br />
je transformace. Inverzní transformací je posunutí o vektor opačný k danému vektoru<br />
posunutí T. Pro kolmé <strong>pro</strong>mítání do půdorysny je M = E 3 a N = E 2 . Nejde tedy o transformaci<br />
a navíc neexistuje inverzní zobrazení (z jednoho průmětu nelze rekonstruovat“<br />
”<br />
<strong>pro</strong>storový objekt).<br />
Dále rozlišíme dva způsoby, jakým jsou v geometrii a jejích aplikacích používány transformace:<br />
Geometrické transformace (bodů): Je zvolen souřadnicový systém. Transformaci jsou<br />
podrobeny body geometrického objektu, který tím mění polohu vzhledem k systému<br />
souřadnic, popř. i svůj tvar.<br />
Transformace systému souřadnic: Transformaci je podroben souřadnicový systém.<br />
Transformace je zvolena např. tak, aby vybraný geometrický objekt získal vzhledem<br />
k novému souřadnicovému systému polohu výhodnou <strong>pro</strong> matematické vyjádření<br />
operací s objektem.<br />
6
1.1. TRANSFORMACE KARTÉZSKÉHO SYSTÉMU SOUŘADNIC 7<br />
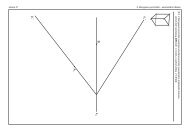
1.1 Transformace kartézského systému souřadnic<br />
V tomto odstavci budeme popisovat transformace souřadnicových soustav v E 3 , ale <strong>pro</strong>vedené<br />
úvahy a výpočty lze snadno aplikovat i na transformace kartézských systémů souřadnic<br />
v rovině, tj. v <strong>pro</strong>storu E 2 (a i v <strong>pro</strong>storech jiné dimenze). V textu použijeme tzv. Kroneckerovo<br />
delta δ ij , které nabývá hodnoty 1 <strong>pro</strong> i = j a hodnoty 0 v případě i ≠ j.<br />
Připomeňme, že kartézskou soustavu<br />
souřadnic v E 3 můžeme<br />
chápat jako uspořádanou čtveřici<br />
(O, e 1 , e 2 , e 3 ), kde O je počátek<br />
soustavy souřadnic a vektory e i jsou<br />
ortonormální, tj. platí <strong>pro</strong> ně<br />
e i · e j = δ ij , i, j = 1, 2, 3. (1.1)<br />
Obrázek 1.1:<br />
Transformaci soustavy souřadnic<br />
používáme, chceme-li zjednodušit<br />
vyjádření objektů, nebo jestliže<br />
<strong>pro</strong> několik objektů chceme využít<br />
jednu souřadnicovou soustavu.<br />
Pro změnu souřadnicové soustavy<br />
odvodíme potřebné vztahy mezi<br />
původnímu souřadnicemi a novými<br />
souřadnicemi.<br />
V <strong>pro</strong>storu E 3 zvolíme dvě kartézské soustavy souřadnic S a S ′ (obr. 1.1):<br />
S : (O, e 1 , e 2 , e 3 ) , S ′ : (O ′ , e ′ 1, e ′ 2, e ′ 3). (1.2)<br />
V soustavě souřadnic S má obecný bod X souřadnice X[x 1 , x 2 , x 3 ] a v S ′ má tentýž bod<br />
X souřadnice X[x ′ 1, x ′ 2, x ′ 3]. V soustavě S vyjádříme počátek O ′ a vektory e ′ i:<br />
O ′ = O +<br />
3∑<br />
b j e j , (1.3)<br />
j=1<br />
Podrobněji lze (1.4) rozepsat na<br />
e ′ i =<br />
3∑<br />
a ji e j , i = 1, 2, 3. (1.4)<br />
j=1<br />
e ′ 1 = a 11 e 1 + a 21 e 2 + a 31 e 3 ,<br />
e ′ 2 = a 12 e 1 + a 22 e 2 + a 32 e 3 , (1.5)<br />
e ′ 3 = a 13 e 1 + a 23 e 2 + a 33 e 3 .
1.1. TRANSFORMACE KARTÉZSKÉHO SYSTÉMU SOUŘADNIC 8<br />
Bod X vyjádříme v obou soustavách souřadnic:<br />
3∑<br />
X = O + x j e j = O ′ +<br />
j=1<br />
3∑<br />
x ′ ie ′ i . (1.6)<br />
i=1<br />
Použijeme-li v (1.6) vyjádření (1.3) a (1.4), dostaneme<br />
O +<br />
neboli<br />
3∑<br />
3∑<br />
x j e j = O + b j e j +<br />
j=1<br />
3∑<br />
j=1 i=1<br />
j=1<br />
j=1 i=1<br />
x ′ i<br />
( 3∑<br />
j=1<br />
)<br />
a ji e j , (1.7)<br />
(<br />
)<br />
3∑<br />
3∑<br />
3∑<br />
x j e j = b j + a ji x ′ i e j . (1.8)<br />
Porovnáním obou stran v (1.8) zjistíme, že <strong>pro</strong> ”<br />
nové“ a ”<br />
staré“ souřadnice platí<br />
x j =<br />
3∑<br />
a ji x ′ i + b j , j = 1, 2, 3. (1.9)<br />
i=1<br />
Transformační rovnice rozepsané <strong>pro</strong> jednotlivá i a j mají tvar<br />
x 1 = a 11 x ′ 1 + a 12 x ′ 2 + a 13 x ′ 3 + b 1 ,<br />
x 2 = a 21 x ′ 1 + a 22 x ′ 2 + a 23 x ′ 3 + b 2 , (1.10)<br />
x 3 = a 31 x ′ 1 + a 32 x ′ 2 + a 33 x ′ 3 + b 3 .<br />
V maticovém tvaru můžeme zapsat rovnice (1.10) jako<br />
X = X ′ · A T + b , (1.11)<br />
kde X[x 1 , x 2 , x 3 ], X ′ [x ′ 1, x ′ 2, x ′ 3], b = (b 1 , b 2 , b 3 ) a matice A má prvky a ij , i = 1, 2, 3, j =<br />
1, 2, 3. Matici A budeme nazývat transformační matice. O této matici se dá dokázat<br />
přímým výpočtem, že platí:<br />
a 1i a 1j + a 2i a 2j + a 3i a 3j = δ ij . (1.12)<br />
Jde o skalární součiny vektorů daných sloupci matice A. Takto určené vektory jsou jednotkové<br />
a vzájemně kolmé. Proto se matice s touto vlastností označují jako ortonormální.<br />
Navíc lze vypočítat, že <strong>pro</strong> determinant ortononální matice A platí<br />
det A = ±1 .<br />
Můžeme tedy rozlišit dva případy orientace S a S ′ :<br />
1. je-li det A = 1, jsou soustavy orientovány souhlasně;<br />
2. je-li det A = −1, jsou soustavy orientovány nesouhlasně.
1.1. TRANSFORMACE KARTÉZSKÉHO SYSTÉMU SOUŘADNIC 9<br />
V geometrii a v řadě aplikací se používají i tzv. afinní souřadnicové soustavy, tj.<br />
soustavy souřadnic, v nichž vektory e 1 , e 2 a e 3 nejsou ortonormální, ale tvoří obecnou<br />
bázi. Přechod od kartézské soustavy souřadnic k afinní soustavě je popsán rovněž vztahem<br />
(1.11), ale matice A je jen regulární (nikoliv nutně ortonormální).<br />
Příklad 1. Uvažujme bod X[1,1,1] daný souřadnicemi v kartézské souřadnicové soustavě<br />
(O, e 1 , e 2 , e 3 ). Určíme souřadnice bodu X v afinní (nekartézské) souřadnicové soustavě<br />
(O, e ′ 1, e ′ 2, e ′ 3),<br />
kde<br />
e ′ 1 = e 1 , e ′ 2 = e 2 , e ′ 3 = e 2 + e 3 .<br />
Řešení: Pokud si načtnete ilustrační obrázek, snadno dojdete při tomto jednoduchém<br />
zadání k výsledku bez výpočtu (doporučujeme, abyste si hypotézu o výsledku vytvořili).<br />
Pokud využijeme vztah (1.11) a uvědomíme-li si, že počátek souřadnicového systému<br />
se nemění, tj. vektor b je nulový, můžeme psát<br />
[1, 1, 1] = [x ′ , y ′ , z ′ ]A T ,<br />
neboli (vzhledem k přepodkládané regularitě matice A existuje matice inverzní)<br />
[x ′ , y ′ , z ′ ] = [1, 1, 1](A T ) −1 .<br />
Matice A má podle (1.5) ve sloupcích souřadnice vektorů nové souřadnicové soustavy<br />
vzhledem k původní souřadnicové soustavě, tj. platí<br />
⎛<br />
1, 0,<br />
⎞<br />
0<br />
⎛<br />
1, 0,<br />
⎞<br />
0<br />
A = ⎝ 0, 1, 1 ⎠ , A T −1 = ⎝ 0, 1, 0 ⎠ .<br />
0, 0, 1<br />
0, −1, 1<br />
Všimněte si, že matice A není ortonormální (uvažujte např. druhý a třetí sloupec, resp.<br />
velikost vektoru daného třetím sloupcem). Výpočet inverzní matice zde neuvádíme, nebot’<br />
jde jen o velmi jednoduché cvičení na uplatnění Jordanovy eliminace, resp. výpočtu pomocí<br />
algebraických doplňků.<br />
Nyní již můžeme psát<br />
⎛<br />
[x ′ , y ′ , z ′ ] = [1, 1, 1] ⎝<br />
1, 0, 0<br />
0, 1, 0<br />
0, −1, 1<br />
⎞<br />
⎠ = [1, 0, 1] .<br />
Věříme, že se výsledek shoduje s předpokládaným výsledkem na základě vašeho úvodního<br />
náčrtku.<br />
□
1.2. HOMOGENNÍ SOUŘADNICE 10<br />
1.2 Homogenní souřadnice<br />
Než přistoupíme k popisu geometrických transformací bodů, zavedeme speciální souřadnice<br />
bodů – tzv. homogenní souřadnice – pomocí nichž se zjednoduší maticový zápis geometrických<br />
transformací.<br />
Uspořádanou čtveřici čísel [x h , y h , z h , w] (w ≠ 0) nazveme pravoúhlé homogenní souřadnice<br />
bodu P v <strong>pro</strong>jektivním rozšíření euklidovského <strong>pro</strong>storu E 3 , platí-li:<br />
x = x h<br />
w ,<br />
y = y h<br />
w ,<br />
z = z h<br />
w<br />
kde čísla x, y, z jsou kartézské souřadnice bodu P . Body, <strong>pro</strong> které je w = 0, odpovídají<br />
vektorům a nazývají se nevlastní body. Tyto body nelze určit jejich kartézskými souřadnicemi.<br />
Projektivní rozšíření euklidovského <strong>pro</strong>storu značíme P (E 3 ) a můžeme říci, že vznikne doplněním<br />
eukleidovského <strong>pro</strong>storu o nevlastní body.<br />
Z definice je patrné, jak lze převádět homogenní souřadnice vlastních bodů (w ≠ 0)<br />
na jejich kartézské souřadnice a naopak.<br />
Příklad 2. Bod A má v daném kartézském systému souřadnic souřadnice [3,2,1]. Za jeho<br />
homogenní souřadnice lze volit trojici [3w, 2w, w, w], kde w ≠ 0. Např. <strong>pro</strong> w = 1 jsou to<br />
souřadnice [3,2,1,1]. Body (v homogenních souřadnicích) B=[3,2,1,0.5] a C=[3,2,1,2] mají<br />
kartézské souřadnice B=[6,4,2] a C=[1,5;1;0,5]. Homogenní souřadnice nevlastního bodu<br />
určeného vektorem OA jsou např. [3,2,1,0].<br />
Obdobně lze zavést pravoúhlé homogenní souřadnice bodu P v rovině.<br />
1.3 Geometrické transformace v E 2 , resp. v P (E 2 )<br />
Zabývejme se nejprve transformacemi v rovině E 2 , resp. v jejím <strong>pro</strong>jektivním rozšíření<br />
P (E 2 ). Bod o souřadnicích [x, y], popř. [x h , y h , w] budeme transformovat do bodu [x ′ , y ′ ],<br />
popř. [x ′ h , y′ h , w′ ].<br />
1.3.1 Posunutí neboli translace<br />
Posunutí (translace) je určeno vektorem posunutí p = (x t , y t ). Souřadnice bodu [x, y] se<br />
transformují rovnicemi<br />
x ′ = x + x t , y ′ = y + y t .<br />
Je zřejmé, že nevlastní bod určený vektorem (x, y) se posunutím nemění.<br />
Použijeme-li homogenní souřadnice, lze obě transformace <strong>pro</strong> vlastní i nevlastní body<br />
zapsat jednotně v maticovém tvaru:<br />
⎛<br />
[x ′ , y ′ , w ′ ] = [x, y, w] ⎝<br />
1, 0, 0<br />
0, 1, 0<br />
x t , y t , 1<br />
⎞<br />
⎠
1.3. GEOMETRICKÉ TRANSFORMACE V E 2, RESP. V P (E 2 ) 11<br />
1.3.2 Otáčení neboli rotace okolo bodu<br />
Otáčení (rotace) kolem počátku O[0, 0] je určeno orientovaným úhlem α. Na obr. 1.2 je<br />
znázorněna odpovídající situace.<br />
Koeficienty odvodíme z podmínky, že body [0,0], [1,0] a [0,1] se otočí do bodů [0, 0],<br />
[cos α, sin α], [− sin α, cos α]. Platí:<br />
x ′ = x cos α − y sin α , y ′ = x sin α + y cos α. (1.13)<br />
Obrázek 1.2: Obrázek 1.3:<br />
Transformační rovnice přepíšeme do maticového tvaru:<br />
⎛<br />
cos α, sin α,<br />
⎞<br />
0<br />
[x ′ , y ′ , w ′ ] = [x, y, w] ⎝ − sin α, cos α, 0 ⎠ . (1.14)<br />
0, 0, 1<br />
Snadno zjistíme, že w ′ = w.<br />
1.3.3 Osová souměrnost<br />
Osová souměrnost je určena osou souměrnosti. Uvedeme transformační rovnice <strong>pro</strong> případ,<br />
kdy osou souměrnosti je některá souřadnicová osa. Platí<br />
x ′ = ix,<br />
y ′ = jy,<br />
kde<br />
i = −1, j = 1 <strong>pro</strong> souměrnost podle osy y;<br />
i = 1, j = −1 <strong>pro</strong> souměrnost podle osy x.<br />
Transformační rovnice <strong>pro</strong> souměrnost podle osy x přepíšeme do maticového tvaru:<br />
⎛<br />
[x ′ , y ′ , w ′ ] = [x, y, w] ⎝<br />
1, 0, 0<br />
0, −1, 0<br />
0, 0, 1<br />
⎞<br />
⎠ . (1.15)
1.3. GEOMETRICKÉ TRANSFORMACE V E 2, RESP. V P (E 2 ) 12<br />
Podobně je možné uvést maticový zápis souměrnosti podle osy y. Souměrnost podle<br />
obecné osy popíšeme pomocí rozkladu na ”<br />
elementární transformace“ – viz odst. 1.3.6<br />
1.3.4 Změna měřítka neboli dilatace<br />
Změna měřítka (dilatace) na souřadnicových osách je určena násobky původních jednotek:<br />
x ′ = s x x , y ′ = s y y .<br />
Je-li s x = s y = s dostaneme stejnolehlost se středem v počátku O[0, 0] a koeficientem stejnolehlosti<br />
s. Maticový zápis transformačních rovnic si snadno představíte. Matice dilatace<br />
je diagonální.<br />
1.3.5 Obecná afinní transformace<br />
Ŕekneme, že tři body A, B, C jsou kolineární, jsou-li kolineární vektory B − A a C − A.<br />
Afinní transformací rozumíme geometrické zobrazení T, které zachovává kolinearitu<br />
bodů a jejich dělící poměr, tj. <strong>pro</strong> každé tři kolineární body A, B, C platí, že body<br />
T(A), T(B), T(C) jsou kolineární a <strong>pro</strong> dělící poměr tří navzájem různých kolineárních<br />
bodů A, B, C platí<br />
(A, B, C) = (T(A), T(B), T(C))<br />
.<br />
Dá se ukázat, že každou afinní transformaci lze popsat v následujícím maticovém<br />
tvaru:<br />
⎛<br />
a 11 , a 12 ,<br />
⎞<br />
0<br />
[x ′ , y ′ , w ′ ] = [x, y, w] ⎝ a 21 , a 22 , 0 ⎠ , (1.16)<br />
p 1 , p 2 , 1<br />
(<br />
a11 ,<br />
kde matice A =<br />
a 21 ,<br />
)<br />
a 12<br />
a 22<br />
je regulární (tj. má nenulový determinant) a p = (p 1 , p 2 )<br />
je vektor posunutí.<br />
Pokud bychom upustili od použití homogenních souřadnic, je možné zapsat vztah<br />
(1.16) <strong>pro</strong> body <strong>pro</strong>storu E 2 je tvaru<br />
(<br />
[x ′ , y ′ a11 ,<br />
] = [x, y]<br />
a 21 ,<br />
)<br />
a 12<br />
a 22<br />
+ (p 1 , p 2 ), (1.17)<br />
neboli stručně:<br />
X ′ = X · A + p, (1.18)<br />
kde p = (p 1 , p 2 ) je vektor posunutí.<br />
Pokud použijeme homogenních souřadnic a označíme<br />
⎛<br />
a 11 , a 12 ,<br />
⎞<br />
0<br />
T = ⎝ a 21 , a 22 , 0 ⎠ , (1.19)<br />
p 1 , p 2 , 1<br />
máme <strong>pro</strong> transformaci vlastních i nevlastních bodů vztah X ′ = X · T.
1.3. GEOMETRICKÉ TRANSFORMACE V E 2, RESP. V P (E 2 ) 13<br />
Příklad 3. Na obr. 1.3 je uveden příklad afinní transformace v rovině. Stín“ je odvozen<br />
”<br />
pomocí afinní transformace s maticí<br />
⎛<br />
1; 0;<br />
⎞<br />
0<br />
[x ′ , y ′ , w ′ ] = [x, y, w] ⎝ 1; −0, 5; 0 ⎠ . (1.20)<br />
0; 0; 1<br />
1.3.6 Skládání transformací<br />
Geometrický objekt je zpravidla podroben posloupnosti uvedených elementárních transformací.<br />
Z asociativního zákona <strong>pro</strong> násobení matic plyne, že matice složené transformace<br />
je součinem matic elementárních transformací.<br />
V předcházejících odstavcích jsme uvedli některé transformace s tím, že jsme předpokládali<br />
speciální určení (např. středem rotace byl počátek, osou souměrnosti byla souřadnicová<br />
osa). Složitější transformace můžeme popsat pomocí rozkladu (dekompozice) na transformace<br />
elementární. Postup vysvětlíme na příkladu.<br />
Příklad 4. Najdeme rovnici rovinné transformace <strong>pro</strong> otáčení kolem bodu A[x A , y A , 1]<br />
o úhel α.<br />
Řešení: Hledanou transformaci složíme ze tří elementárních transformací. Posunutím<br />
o vektor p = (−x A , −y A ) se bod A ztotožní s počátkem O. Po otočení bodů kolem<br />
počátku o úhel α posuneme výsledné body zpět o vektor −p . Posloupnost transformací<br />
zapíšeme za využití homogenních souřadnic v maticovém tvaru:<br />
⎛<br />
X ′ = X ⎝<br />
1, 0, 0<br />
0, 1, 0<br />
−x A , −y A , 1<br />
⎞ ⎛<br />
⎠ ⎝<br />
cos α, sin α, 0<br />
− sin α, cos α, 0<br />
0, 0, 1<br />
⎞ ⎛<br />
⎠ ⎝<br />
1, 0, 0<br />
0, 1, 0<br />
x A , y A , 1<br />
Provedeme-li vynásobení uvedených tří matic, obdržíme matici dané transformace ve<br />
tvaru ⎛<br />
cos α, sin α,<br />
⎞<br />
0<br />
⎝ − sin α, cos α, 0 ⎠ .<br />
x A (1 − cos α) + y A sin α, y A (1 − cos α) − x A sin α, 1<br />
1.3.7 Inverzní geometrická transformace<br />
Pro inverzní transformaci T −1 k dané transformaci T platí, že složením těchto dvou<br />
transformací je identita, tj. transformace, která každému bodu X přiřadí týž bod, tj. X ′ =<br />
X. Maticí identity je samozřejmě jednotková matice I. Označme T matici transformace<br />
T a L matici transformace T −1 . Pro tyto matice však musí platit vztah<br />
T · L = L · T = I,<br />
tj. L = T −1 – matice inverzní transformace je inverzní maticí k matici dané transformace.<br />
⎞<br />
⎠ .<br />
□
1.4. GEOMETRICKÉ TRANSFORMACE V E 3, RESP. V P (E 3 ) 14<br />
1.4 Geometrické transformace v E 3 , resp. v P (E 3 )<br />
Uvedeme přehled elementárních afinních transformací v <strong>pro</strong>storu E 3 , resp. v P (E 3 ). Transformační<br />
rovnice zapíšeme v maticovém tvaru. Postupovat budeme rychleji, nebot’ v mnoha<br />
případech je určení transformací v P (E 3 ) analogické k uvedeným poznatkům <strong>pro</strong> <strong>pro</strong>stor<br />
P (E 2 ). Podrobnější výklad je uveden jen tam, kde tato analogie neexistuje.<br />
1.4.1 Posunutí neboli translace<br />
Pro posunutí (translaci) určenou vektorem posunutí p = (x t , y t , z t ) máme transformační<br />
rovnici:<br />
⎛<br />
⎞<br />
1, 0, 0, 0<br />
[x ′ , y ′ , z ′ , w ′ ] = [x, y, z, w] ⎜ 0, 1, 0, 0<br />
⎟<br />
⎝ 0, 0, 1, 0 ⎠ .<br />
x t , y t , z t , 1<br />
1.4.2 Otáčení neboli rotace okolo osy<br />
Otáčení (rotace) je určeno osou otáčení a orientovaným úhlem otáčení. Uvedeme matici<br />
R x,α <strong>pro</strong> otáčení kolem souřadnicové osy x o úhel α, matici R y,β <strong>pro</strong> otáčení kolem osy y<br />
o úhel β a matici R z,γ <strong>pro</strong> otáčení kolem osy z o úhel γ. Snadno stanovíme matici R z,γ ,<br />
nebot’ vztahy <strong>pro</strong> transformaci složky x a y jsou analogické s rotací bodu okolo počátku –<br />
vztah (1.13), souřadnice z se nemění. Další případy, tj. popis rotace okolo osy x a y,<br />
získáme cyklickou záměnou os – tab. 1.1.<br />
Osa rotace 1. osa 2. osa<br />
z x y<br />
x y z<br />
y z x<br />
Tabulka 1.1:<br />
Pro hledané matice platí:<br />
⎛<br />
R x,α =<br />
⎜<br />
⎝<br />
1, 0, 0, 0<br />
0, cos α, sin α, 0<br />
0, − sin α, cos α, 0<br />
0, 0, 0, 1<br />
R z,γ =<br />
⎛<br />
⎜<br />
⎝<br />
⎞<br />
⎟<br />
⎠ , R y,β =<br />
⎛<br />
⎜<br />
⎝<br />
cos γ, sin γ, 0, 0<br />
− sin γ, cos γ, 0, 0<br />
0, 0, 1, 0<br />
0, 0, 0, 1<br />
cos β, 0, − sin β, 0<br />
0, 1, 0, 0<br />
sin β, 0, cos β, 0<br />
0, 0, 0, 1<br />
Všimněte si, že souměrnost podle osy můžeme v <strong>pro</strong>storu P (E 3 ) nahradit rotací okolo<br />
dané osy o úhel ϕ = π. V <strong>pro</strong>storu P (E 2 ) je rotace okolo bodu o úhel ϕ = π souměrností<br />
podle daného bodu (středu).<br />
⎞<br />
⎟<br />
⎠ .<br />
⎞<br />
⎟<br />
⎠ ,
1.4. GEOMETRICKÉ TRANSFORMACE V E 3, RESP. V P (E 3 ) 15<br />
1.4.3 Souměrnost podle roviny<br />
Souměrnost podle roviny je určena rovinou souměrnosti. Uvedeme rovnice <strong>pro</strong> transformaci<br />
bodu souměrností podle jednotlivých souřadnicových rovin:<br />
⎛<br />
⎞<br />
i, 0, 0, 0<br />
[x ′ , y ′ , z ′ , w ′ ] = [x, y, z, w] ⎜ 0, j, 0, 0<br />
⎟<br />
⎝ 0, 0, k, 0 ⎠ ,<br />
0, 0, 0, 1<br />
kde<br />
i = -1, j = 1, k = 1 <strong>pro</strong> souměrnost podle roviny yz,<br />
i = 1, j = -1, k = 1 <strong>pro</strong> souměrnost podle roviny xz,<br />
i = 1, j = 1, k = -1 <strong>pro</strong> souměrnost podle roviny xy.<br />
1.4.4 Dilatace<br />
Dilatace neboli změna měřítka na souřadnicových osách je určena nenulovými násobky<br />
s x , s y , s z původních jednotek. Maticově můžeme psát:<br />
⎛<br />
⎞<br />
s x 0 0 0<br />
[x ′ , y ′ , z ′ , w ′ ] = [x, y, z, w] ⎜ 0 s y 0 0<br />
⎟<br />
⎝ 0 0 s z 0 ⎠ .<br />
0 0 0 1<br />
Podobně jako v případu rovinné geometrie dostaneme i zde <strong>pro</strong> s = s x = s y<br />
stejnolehlost se středem stejnolehlosti v počátku a s koeficientem s.<br />
= s z<br />
1.4.5 Obecná afinní transformace a <strong>pro</strong>jektivní transformace<br />
Podobně jako v rovinném případě můžeme i v <strong>pro</strong>storu P (E 3 ) popsat každou afinní transformaci<br />
v následujícím maticovém tvaru:<br />
⎛<br />
⎞<br />
a 11 , a 12 , a 13 , 0<br />
[x ′ , y ′ , z ′ , w ′ ] = [x, y, z, w] ⎜ a 21 , a 22 , a 23 , 0<br />
⎟<br />
⎝ a 31 , a 32 , a 33 , 0 ⎠ , (1.21)<br />
p 1 , p 2 , p 3 , 1<br />
⎛<br />
⎞<br />
a 11 , a 12 , a 13<br />
kde matice A = ⎝ a 21 , a 22 , a 23<br />
⎠ je regulární (tj. má nenulový determinant).<br />
a 31 , a 32 , a 33<br />
Opět můžeme uvést, že uplatnění obecné afinní transformace je popsáno maticovým<br />
součinem X ′ = X · T, kde T je matice transformace.<br />
Pro zvídavého čtenáře můžeme ještě doplnit, že obecnější transformací je tzv. <strong>pro</strong>jektivní<br />
transformace. Ta sice zachovává kolinearitu bodů, ale již může měnit dělící poměr<br />
bodů (nemění však podíl dělících poměrů – tzv. dvojpoměr). Popis takového transformace<br />
je tvaru (1.21) s tím, že poslední sloupec transformační matice může obsahovat i nenulové<br />
prvky. V afinní transformaci vlastnímu bodu byl přiřazen vždy bod vlastní (a nevlastnímu
1.5. SKLÁDÁNÍ TRANSFORMACÍ A INVERZNÍ TRANSFORMACE 16<br />
bod nevlastní). Toto již neplatí v případě <strong>pro</strong>jektivní transformace. V důsledku to znamená,<br />
že <strong>pro</strong>jektivní transformace obecně nezachovává rovnoběžnost (afinní transformace<br />
rovnoběžnost zachovává). Příkladem <strong>pro</strong>jektivního zobrazení je např. perspektivní pohled<br />
apod.<br />
1.5 Skládání transformací a inverzní transformace<br />
Vše, co jsme uvedli o skládání transformací a o inverzní transformaci v rovinném případě,<br />
je platné i <strong>pro</strong> transformace v <strong>pro</strong>storu P (E 3 ).<br />
Pro ilustraci uvedeme alespoň jeden příklad.<br />
Příklad 5. Sestavíme matici souměrnosti podle roviny x−2z +3 = 0. Určíme pak obrazy<br />
bodů O[0, 0, 0], R[1, 1, 1] a Q[−3, 0, 5] a obraz směru (nevlastního bodu) daného vektorem<br />
(1, 0, −2).<br />
Řešení: Zvolíme postup, který byl použit již v části věnované rovinným transformacím,<br />
tj. <strong>pro</strong>vedeme rozklad (dekompozici) hledané transformace T na elementární transformace.<br />
Daná rovina je zřejmě rovnoběžná s osou y (koeficient u y je nulový). Transformaci T tedy<br />
získáme složením:<br />
• posunutí P (rovina souměrnosti bude po posunutí <strong>pro</strong>cházet osou y),<br />
• rotace R (rovinu souměrnosti převedeme do polohy totožné s rovinou xy),<br />
• souměrnosti S podle roviny xy,<br />
• rotace R −1 ,<br />
• posunutí P −1 .<br />
Poslední dvě transformace (pozor na pořadí) umístí zpět rovinu souměrnosti do původní<br />
polohy. Píšeme<br />
T = P −1 ◦ R −1 ◦ S ◦ R ◦ P .<br />
Vektor normály dané roviny je n = (1, 0, −2). Určíme dále alespoň jeden bod roviny,<br />
např. bod X ∈ x. Volíme tedy z = 0 a máme X[−3, 0, 0]. První transformací bude posunutí<br />
P o vektor (3, 0, 0). Rovina souměrnosti <strong>pro</strong>chází po <strong>pro</strong>vedení transformace P počátkem<br />
a osou y. Nyní <strong>pro</strong>vedeme rotaci R, v níž rovina přejde do některé souřadnicové roviny,<br />
např. xy. Stanovíme úhel otočení α jako odchylku rovin. Použijeme k tomu normálové<br />
vektory n a z, kde z=(0,0,1) je normálový vektor roviny xy. Platí<br />
cos α =<br />
|n · z|<br />
|n| · |z| ,<br />
tj.<br />
cos α = 2 √<br />
5<br />
= 2 5√<br />
5.<br />
Pomocí vztahu sin 2 α = 1 − cos 2 α vypočteme sin α = √ 5<br />
5 .
1.6. CVIČENÍ 17<br />
Označme matice, které odpovídají daným transformacím stejnými písmeny, jako jsou<br />
označeny dílčí transformace (R bude matice rotace R apod.). Pro matici T výsledné<br />
transformace platí (pozor na pořadí):<br />
T = P · R · S · R −1 · P −1 ,<br />
tj.<br />
T =<br />
⎛<br />
⎜<br />
⎝<br />
1, 0, 0, 0<br />
0, 1, 0, 0<br />
0, 0, 1 0<br />
3, 0, 0, 1<br />
⎛<br />
· ⎜<br />
⎝<br />
2<br />
5<br />
⎞<br />
⎟<br />
⎠ ·<br />
⎛<br />
⎜<br />
⎝<br />
√ √<br />
2<br />
5 5, 0, − 5<br />
, 0 5<br />
0, 1, 0, 0<br />
√<br />
5<br />
, 0, 2<br />
5 5√<br />
5, 0<br />
√ √<br />
5, 0,<br />
5<br />
, 0 5<br />
0, 1, 0, 0<br />
, 0, 2<br />
5 5√<br />
5, 0<br />
− √ 5<br />
0, 0, 0, 1<br />
0, 0, 0, 1<br />
⎞ ⎛<br />
⎟<br />
⎠ ·<br />
⎜<br />
⎝<br />
⎞<br />
⎟<br />
⎠ ·<br />
⎛<br />
⎜<br />
⎝<br />
1, 0, 0, 0<br />
0, 1, 0, 0<br />
0, 0, 1 0<br />
−3, 0, 0, 1<br />
1, 0, 0, 0<br />
0, 1, 0, 0<br />
0, 0, −1 0<br />
0, 0, 0, 1<br />
⎞<br />
⎟<br />
⎠ .<br />
⎞<br />
⎟<br />
⎠ ·<br />
Provedeme-li naznačené násobení matic, obdržíme matici výsledné transformace:<br />
⎛<br />
3<br />
, 0, 4<br />
, 0 ⎞<br />
5 5<br />
T = ⎜ 0, 1, 0, 0<br />
⎝ 4<br />
, 0, − 3, 0<br />
⎟<br />
⎠ .<br />
5 5<br />
− 6, 0, 12<br />
, 1 5 5<br />
Pro určení nové (transformované) polohy daných vlastních bodů O, R, Q a nevlastního<br />
bodu [1, 0, −2, 0] stačí vynásobit homogenní souřadnice daných maticí T. S výhodou<br />
můžeme tuto operaci zapsat ve tvaru (řádky první matice jsou dány homogenními souřadnicemi<br />
zadaných bodů):<br />
⎛<br />
⎞ ⎛<br />
3<br />
⎜<br />
⎟<br />
⎝<br />
⎠ ·<br />
, 0, 4<br />
, 0 ⎛<br />
− 6 5 5<br />
⎜ 0, 1, 0, 0<br />
⎟<br />
⎝ 4<br />
⎠ = , 0, 12<br />
, 1 ⎞<br />
5 5<br />
1<br />
⎜ , 1, 13<br />
, 1<br />
5 5 ⎟<br />
⎝<br />
⎠ .<br />
0, 0, 0, 1<br />
1, 1, 1, 1<br />
−3, 0, 5, 1<br />
1, 0, −2, 0<br />
⎞<br />
, 0, − 3, 0<br />
5 5<br />
− 6, 0, 12<br />
, 1 5 5<br />
1, 0, −3, 1<br />
−1, 0, 2, 0<br />
Máme tedy T(O) = [− 6, 0, 12, 1], T(R) = [ 1, 1, 13 , 1], T(Q) = [1, 0, −3, 1] a obrazem<br />
5 5 5 5<br />
vektoru s = (1, 0, −2) je vektor T(s) = (−1, 0, 2), tj. vektor opačný (jde vlastně o obraz<br />
normálového vektoru zadané roviny souměrnosti). Oba vektory s a T(s) určují stejný<br />
nevlastní bod, tj. bod, který je v dané transformaci samodružný.<br />
□<br />
1.6 Cvičení<br />
1.1 Je dána jednotková krychle ABCDA ′ B ′ C ′ D ′ . Napište transformační rovnice přechodu<br />
od kartézského souřadnicového systému {A, AB, −→<br />
AD, −→<br />
AA −→<br />
′ } k systému {C ′ −→<br />
, C ′ D ′<br />
−→<br />
, C ′ B ′ , C −→<br />
′ C}.<br />
[x = −x ′ + 1, y = −y ′ + 1, z = −z ′ + 1]
1.6. CVIČENÍ 18<br />
1.2 Rozhodněte, zda matice<br />
A =<br />
⎛<br />
⎜<br />
⎝<br />
1<br />
, − √ 2<br />
, − 1<br />
2 2 2<br />
1<br />
, √<br />
2<br />
, − 1<br />
2 2 2<br />
− √ 2<br />
, 0, √<br />
2<br />
2 2<br />
⎞<br />
⎟<br />
⎠<br />
je transformační maticí <strong>pro</strong> přechod mezi dvěma kartézskými soustavami souřadnic.<br />
[využijeme vztahů (1.12) – není]<br />
1.3 Sestavte transformační rovnice přechodu mezi dvěma kartézskými systémy souřadnic,<br />
jestliže nový systém vznikne z původního otočením kolem osy z o úhel ϕ = − π.<br />
4<br />
[x = √ 2<br />
2 (x′ + y ′ ), y = √ 2<br />
2 (−x′ + y ′ ), z = z ′ ]<br />
1.4 Určete nové souřadnice bodu M[2, −1, 3], jestliže se kartézská souřadnicová soustava<br />
otočí okolo osy z o orientovaný úhel α = π. 6 [ √3<br />
[ −<br />
1<br />
, −1 − √ 3<br />
]] , 3 2 2<br />
1.5 Sestavte matici geometrické transformace v E 2 , která vznikne složením (v tomto<br />
pořadí) rotace okolo bodu S[1, 2] o úhel 45 o a dilatace, v níž se mění měřítko na ose<br />
x na poloviční.<br />
⎡ ⎛ √<br />
2<br />
, √ ⎤<br />
2<br />
, 0<br />
4 2<br />
⎢<br />
⎣T =<br />
⎜<br />
⎝<br />
− √ 2<br />
, √<br />
2<br />
4<br />
1<br />
+ √ 2<br />
, 2 − 3<br />
2 4 2<br />
⎞<br />
√ , 0 ⎟⎥<br />
2<br />
⎠⎦<br />
2, 1<br />
1.6 Určete obrazy bodů S[1, 2] a O[0, 0] a vektoru a = (1, 1) v transformaci podle<br />
předcházejícího příkladu. [<br />
T(A) = [ 1, 2] , T(0) = [ 1 + √ 2<br />
, 2 − √ √ ]<br />
3<br />
2 2 4 2 2] , T(a) = (0, 2)<br />
1.7 Určete matici inverzní transformace k transformaci podle cvičení 5 z této kapitoly.<br />
[ určete T −1 , příp. (pořadí!) T −1 = R S,−45 0 ◦ D sx=2 ]<br />
1.8 V <strong>pro</strong>storu E 2 určete afinní transformaci, která má samodružné body O[0, 0] a A[1, 0]<br />
a obrazem bodu B[0, 1] je bod B ′ [1, 1].<br />
⎡ ⎛ ⎞⎤<br />
1, 0, 0<br />
⎣T = ⎝ 1, 1, 0 ⎠⎦<br />
0, 0, 1<br />
1.9 Sestavte matici rotace – jako geometrické transformace v E 3 , je-li osou rotace přímka<br />
o : x = −t , y = 2t , z = −1 ⎡ .<br />
⎤<br />
⎛<br />
T = P −1<br />
o→o 1<br />
◦ R −1<br />
o 1 →y ◦ R y,ϕ ◦ R o1 →y ◦ P o→o1 ;<br />
4<br />
cos ϕ + 1, 2<br />
cos ϕ − 2, − ⎞<br />
2√ 5<br />
sin ϕ, 0<br />
5 5 5 5 5<br />
2<br />
⎢ T = ⎜<br />
cos ϕ − 2, 1<br />
cos ϕ + 4, − √ 5<br />
sin ϕ, 0<br />
5 5 5 5 5 ⎣ ⎝<br />
2 √ √<br />
5<br />
sin ϕ, 5<br />
⎟ ⎥<br />
sin ϕ, cos ϕ, 0 ⎠ ⎦<br />
5 5<br />
2 √ √<br />
5<br />
sin ϕ, 5<br />
sin ϕ, cos ϕ − 1, 1 5 5
1.7. KONTROLNÍ OTÁZKY 19<br />
1.10 Maticově popište geometrickou transformaci, která vznikne složením rotace okolo<br />
osy z a posunutí ve směru ⎡ této osy (jde o popis šroubového ⎛ pohybu). ⎞⎤<br />
cos ϕ, sin ϕ, 0, 0<br />
⎢<br />
⎣ matice transformace T = ⎜ − sin ϕ, cos ϕ, 0, 0<br />
⎟⎥<br />
⎝ 0, 0, 1, 0 ⎠⎦<br />
0, 0, v 0 ϕ, 1<br />
1.7 Kontrolní otázky<br />
1.1 Jak se liší homogenní souřadnice vlastního a nevlastního bodu.<br />
1.2 Pomocí geometrických transformací v rovině uved’te příklad dvou matic A a B, <strong>pro</strong><br />
něž A · B = B · A, tj. případ zaměnitelného pořadí dvou transformací.<br />
1.3 Pomocí geometrických transformací v rovině uved’te příklad dvou matic A a B, <strong>pro</strong><br />
něž A · B ≠ B · A, tj. případ nezaměnitelného pořadí dvou transformací.<br />
1.4 Matice transformace v P (E 3 ) je tvaru<br />
⎛<br />
T =<br />
⎜<br />
⎝<br />
α, 0, 0, 0<br />
0, β, 0, 0<br />
0, 0, γ, 0<br />
0, 0, 0, 1<br />
Do následující tabulky doplňte <strong>pro</strong> dané hodnoty diagonálních prvků, o jaké souměrnosti<br />
se jedná:<br />
⎞<br />
⎟<br />
⎠ .<br />
α β γ souměrnost podle<br />
-1 1 1<br />
-1 -1 1<br />
-1 -1 -1<br />
1 -1 1<br />
1 1 -1<br />
-1 1 -1<br />
1 -1 -1<br />
1.5 K maticím souměrností z předcházející otázky stanovte inverzní transformace a formulujte<br />
obecné tvrzení o inverzní transformaci k souměrnosti.<br />
1.6 Popište, jak je možné stanovit parametrické vyjádření translačních (vznikají posuvným<br />
pohybem křivky), rotačních a šroubových ploch pomocí transformací.
Kapitola 2<br />
Křivky<br />
2.1 Základní pojmy<br />
Křivkou rozumíme dráhu pohybujícího se bodu.<br />
Křivka je jednoparametrická množina bodů, nebot’ pohyb je závislý na jediném parametru<br />
– zpravidla jde o čas.<br />
Obrázek 2.1: K definici křivky<br />
Pomocí matematických <strong>pro</strong>středků je možné definovat regulární křivku takto:<br />
Definice 1. Regulární křivkou třídy C n v E 3 rozumíme množinu K ⊂ E 3 (obr. 2.1), <strong>pro</strong><br />
níž existuje vektorová funkce P (t), t ∈ I tak, že<br />
(a) P : I → K, I je otevřený interval,<br />
(b) P je třídy C n ,<br />
(c) |P ′ (t 0 )| ≠ 0 <strong>pro</strong> všechna t 0 ∈ I,<br />
(d) t 1 ≠ t 2 ⇒ P (t 1 ) ≠ P (t 2 ).<br />
20
2.1. ZÁKLADNÍ POJMY 21<br />
Je samozřejmě možné omezit se v definici na rovinu, tedy na <strong>pro</strong>stor E 2 , tedy na<br />
křivky ležící v rovině. Rovinnou křivkou rozumíme navíc ale i křivku, která je definována<br />
v <strong>pro</strong>storu E 3 , ale všechny její body leží v jedné rovině.<br />
Křivkou (bez přívlastku ”<br />
regulární“) zpravidla rozumíme množinu bodů, která je po<br />
částech regulární křivkou, tj. připouštíme, že v konečném počtu bodů jsou porušeny uvedené<br />
podmínky.<br />
Uvedená definice využívá tzv. vektorový popis křivky, který lze ale snadno rozepsat<br />
do parametrických rovnic.<br />
Příklad 6. Např. elipsa má parametrické vyjádření<br />
její vektorový popis v E 2 je<br />
Rovnice<br />
x = a cos t, y = b sin t, t ∈ (0, 2π); a, b > 0,<br />
P (t) = (a cos t, b sin t).<br />
x = r cos t, y = r sin t, z = 2t, t ∈ (−π, π)<br />
jsou vyjádřením části šroubovice. Vektorově můžeme psát<br />
P (t) = (r cos t, r sin t, 2t).<br />
I rovinnou křivku můžeme zapsat jako křivku v <strong>pro</strong>storu např.<br />
je vyjádřením úsečky v <strong>pro</strong>storu.<br />
2.1.1 Tečna a normála křivky<br />
x = 1 + t, y = t, z = 2 − 0.5t, t ∈ 〈5, 6〉<br />
Na křivce zvolíme bod T a v jeho okolí bod A. Tečna křivky je limitní polohou přímky<br />
AT <strong>pro</strong> A → T (obr.2.2).<br />
Pomocí vektoru první derivace můžeme definovat tečnu křivky jako přímku určenou<br />
bodem křivky a tečným vektorem. Píšeme X = T + su, kde<br />
u = (x ′ (t), y ′ (t), z ′ (t)), u ≠ o<br />
je tečný vektor a T [T 1 , T 2 , T 3 ] dotykový bod.<br />
Sečna je spojnice dvou bodů křivky.<br />
Asymptota je tečna v nevlastním bodě.<br />
Normála v bodě T je každá přímka kolmá k tečně v bodě T <strong>pro</strong>cházející bodem T .<br />
Normálová rovina je množina všech normál v bodě křivky. Je to rovina kolmá k<br />
tečně.<br />
Úhel křivek k 1 , k 2 (<strong>pro</strong>tínajících se) je úhel jejich tečen v jejich průsečíku (obr.2.3).<br />
Rovnoběžným nebo středovým průmětem <strong>pro</strong>storové křivky je rovinná křivka. Průmětem<br />
tečny je tečna nebo bod.
2.1. ZÁKLADNÍ POJMY 22<br />
Obrázek 2.2: Obrázek 2.3:<br />
2.1.2 Klasifikace bodů křivky<br />
Bod, ve kterém má křivka jedinou tečnu určenou jediným nenulovým vektorem, nazýváme<br />
regulární bod; v opačném případě bod nazveme singulární.<br />
Různé typy singulárních bodů vidíme na obr. 2.4. Bod A v obrázku 2.4a) se nazývá<br />
uzlový bod , body B a C v obrázku 2.4b) a c) jsou body vratu a bod D v obrázku<br />
2.4d) je inflexní bod (ten je speciálním případem regulárního bodu).<br />
Obrázek 2.4:<br />
2.1.3 Rektifikace<br />
Rektifikace oblouku křivky je rozvinutí oblouku křivky na přímku, tj. sestrojení úsečky<br />
stejné velikosti, jako je délka oblouku křivky. Nejjednodušší rektifikace je založena na<br />
náhradě křivky lomenou čarou (lineární interpolace) - obr. 2.5 . Na křivce zvolíme vhodný<br />
počet bodů (na obr. 2.5 jsou označeny A 1 , A 2 , . . .), spojíme lomenou čarou a jednotlivé<br />
úsečky přeneseme na přímku. Je zřejmé, že čím více bodů zvolíme, tím přesněji můžeme<br />
zjistit délku křivky.<br />
Věta 1. Délku oblouku <strong>pro</strong>storové křivky, <strong>pro</strong> kterou známe její parametrické vyjádření,<br />
můžeme vypočítat pomocí integrálu<br />
∫ t2<br />
√<br />
x′ (t) 2 + y ′ (t) 2 + z ′ (t) 2 dt,<br />
t 1
2.1. ZÁKLADNÍ POJMY 23<br />
Obrázek 2.5: Obrázek 2.6:<br />
kde t 1 a t 2 jsou krajní body oblouku křivky.<br />
K rektifikaci oblouku kružnice se často užívalo přibližných konstrukcí jako např. konstrukce<br />
Kochaňského, d’Ocagneova nebo Sobotkova. Použití počítačů v technických oborech<br />
nám umožňuje zjistit délku oblouku mnohem pohodlněji i přesněji, <strong>pro</strong>to i zde budeme<br />
používat bud’ výpočtu pomocí integrálu, nebo pomocí lineární interpolace (jako součet<br />
délek stran nahrazující lomené čáry).<br />
Obráceně můžeme také navinout úsečku na křivku, tj. na dané křivce najdeme oblouk,<br />
jehož délka se rovná velikosti dané úsečky.<br />
2.1.4 Oskulační rovina a oskulační kružnice<br />
Je dán bod T a tečna t v tomto bodě, na křivce zvolíme v okolí bodu T bod A. Rovina α je<br />
určená bodem A a tečnou t. Limitní poloha této roviny při A → T se nazývá oskulační<br />
rovina . V oskulační rovině leží jedna z normál křivky v daném bodě. Tuto normálu<br />
nazýváme hlavní normála . Normála kolmá k oskulační rovině se nazývá binormála.<br />
Určení rovnice oskulační roviny můžeme <strong>pro</strong>vést podle následujícího tvrzení:<br />
Věta 2. Pokud jsou vektory P ′ a P ′′ v daném bodě P (t 0 ) křivky nekolineární, tj. daný bod<br />
křivky není jejím inflexním bodem, pak oskulační rovina křivky v daném bodě je určena<br />
vektory P ′ a P ′′ , tj. rovnici oskulační roviny můžeme psát ve tvaru<br />
X(u, v) = P (t 0 ) + uP ′ (t 0 ) + vP ′′ (t 0 ) , u ∈ R, v ∈ R .<br />
Na křivce k zvolíme libovolný regulární bod A. Dále na křivce zvolíme ještě další dva<br />
body A 1 , A 2 . Body A, A 1 , A 2 je určena kružnice l. Oskulační kružnice křivky k v bodě<br />
A je limitní polohou kružnice l(A, A 1 , A 2 ), jestliže A 1 → A a A 2 → A (obr.2.6). Střed<br />
této kružnice nazýváme střed křivosti a poloměr r této kružnice nazýváme poloměr<br />
křivosti. Číslo 1 k = 1 nazýváme první křivostí (flexí) křivky k v bodě A. Kromě toho<br />
r<br />
u křivek pracujeme i s druhou křivostí (torzí) 2 k, která vyjadřuje <strong>pro</strong>storové zakřivení<br />
křivky, tedy zakřivení vzhledem k oskulační rovině. Návod k určení obou křivostí dává<br />
následující věta.
2.1. ZÁKLADNÍ POJMY 24<br />
Věta 3. Pro regulární křivku s obecným parametrem platí<br />
( 1 k) 2 = (P ′ × P ′′ ) 2<br />
(P ′ · P ′ ) 3<br />
2 k = (P ′ , P ′′ , P ′′′ )<br />
(P ′ × P ′′ ) 2<br />
Oskulační kružnice se v malém okolí bodu A velmi málo liší od křivky k, a <strong>pro</strong>to<br />
můžeme v okolí bodu A nahradit křivku její oskulační kružnicí. Toto nahrazení se používá<br />
např. u kuželoseček, kde známe jednoduché konstrukce oskulačních kružnic ve vrcholech.<br />
Oskulační kružnice leží v oskulační rovině křivky a má poloměr rovný převrácené hodnotě<br />
první křivosti dané křivky v daném bodě. Pro polohový vektor středu S křivosti křivky v<br />
bodě daném parametrem t 0 máme<br />
S = P (t 0 ) + 1<br />
1<br />
k(t 0 ) n.<br />
Křivky se dotýkají v daném bodě, mají-li v něm společnou tečnu.<br />
Křivka může být dána i jiným způsobem, než jako dráha bodu, např. jako obálka<br />
jednoparametrické soustavy křivek, ekvidistanta, evoluta, evolventa, cykloida nebo jako<br />
průnik ploch.<br />
Některé z těchto křivek dále popíšeme, ale více se zaměříme na <strong>pro</strong>storovou křivku<br />
důležitou <strong>pro</strong> technickou praxi – šroubovici.<br />
Obrázek 2.7: Obrázek 2.8:<br />
Příklad 7. Pro <strong>pro</strong>storovou křivku danou vektorovou funkcí P (t), t ∈ I, určete jednotkové<br />
vektory určující tečnu, hlavní normálu a binormálu tak, aby tvořily pravotočivý systém.<br />
Řešení: Hledané jednotkové a vzájemně kolmé vektory označme t, n a b. Je zřejmé, že<br />
t = P ′<br />
|P ′ |<br />
(jde o normování tečného vektoru). Vektory P ′ a P ′′ určují (pokud jde o neinflexní bod)<br />
spolu s daným bodem křivky oskulační rovinu. Místo vektoru P ′ můžeme uvažovat již
2.1. ZÁKLADNÍ POJMY 25<br />
jednotkový vektor t. Pomocí vektorového součinu určíme vektor kolmý k oskulační rovině<br />
a <strong>pro</strong>vedeme jeho normování. Pro vektor binormály tedy platí<br />
b = t × P ′′<br />
|t × P ′′ | .<br />
Jednotkový vektor hlavní normály (pozor na pořadí vektorů) určíme již snadno pomocí<br />
vektorového součinu jednotkových a na sebe kolmých vektorů (není již nutné normování):<br />
2.1.5 Obálka<br />
n = b × t.<br />
Je dána jednoparametrická soustava křivek v rovině. Křivka u, které se dotýkají všechny<br />
křivky soustavy se nazývá obálka soustavy křivek. Dotykový bod obálky a křivky<br />
daného systému se nazývá charakteristický bod.<br />
Na obrázku 2.7a) je křivka u obálkou soustavy přímek, na obrázku 2.7b) je dvojice<br />
křivek u, u ′ obálkou soustavy elips. Na každé obálce je vyznačeno několik charakteristických<br />
bodů.<br />
Věta 4. Uvažujeme rovinnou křivku danou implicitní rovnicí F (x, y, α) = 0, kde α je<br />
parametr popisující jednotlivé křivky dané soustavy křivek. Necht’ ∂2 F<br />
≠ 0, tj. tvořící<br />
∂α 2<br />
křivka má s obalovou křivkou lokálně společný jen bod, tedy křivka se svým pohybem nere<strong>pro</strong>dukuje.<br />
Pak souřadnice bodů obalové křivky jsou řešením soustavy<br />
F (x, y, α) = 0 ,<br />
∂F (x, y, α)<br />
∂α<br />
= 0.<br />
Uvažujeme-li α jako parametr, dostaneme obalovou křivku a α je její parametr.<br />
Příklad 8. Určete obálku systému kružnic (x − α) 2 + y 2 = 1.<br />
Řešení: Podle předcházející věty máme rovnice:<br />
Dostáváme dvě rovnice<br />
(x − α) 2 + y 2 = 1 ∂F<br />
∂α<br />
= 2(x − α)(−1) = 0 .<br />
(x − α) 2 + y 2 − 1 = 0<br />
x − α = 0<br />
Dosazením z druhé rovnic do první, máme tuto rovnici y 2 − 1 = 0, tj. y = ±1. Obálkou<br />
systému křivek jsou tedy dvě přímky y = 1 a y = −1. Výsledkem je samozřejmě v souladu<br />
s tím, že v zadání šlo o jednotkovou kružnici, které se posouvá svým středem po ose x.<br />
□<br />
□
2.1. ZÁKLADNÍ POJMY 26<br />
2.1.6 Ekvidistanta<br />
Máme dánu rovinnou křivku k. Okolo každého bodu této křivky opíšeme kružnici o<br />
poloměru r. Jestliže existuje obálka této soustavy kružnic nazýváme ji ekvidistantou<br />
křivky k - obr. 2.8.<br />
Body ekvidistanty můžeme získat také jiným způsobem: v každém bodě A křivky k<br />
sestrojíme hlavní normálu a naneseme na ni od bodu A úsečku o velikosti r. Tento postup<br />
lze použít i <strong>pro</strong> <strong>pro</strong>storové křivky.<br />
k<br />
h<br />
c<br />
e<br />
p<br />
Obrázek 2.9: Obrázek 2.10:<br />
2.1.7 Cykloida<br />
Při odvalování křivky k po pevné křivce p opíše každý bod roviny křivku, kterou nazýváme<br />
trajektorie (dráha).<br />
Při odvalování kružnice k po přímce p opíše každý bod kružnice (<strong>pro</strong>stou) cykloidu.<br />
Bod uvnitř kružnice k opíše zkrácenou cykloidu a bod vně kružnice opíše <strong>pro</strong>dlouženou<br />
cykloidu. Na obrázku 2.9 je znázorněna cykloida c, zkrácená cykloida e a <strong>pro</strong>dloužená<br />
cykloida h.<br />
2.1.8 Evoluta a evolventa<br />
Jestliže existuje obálka hlavních normál rovinné křivky, nazýváme ji evolutou. Lze ji pak<br />
také získat jako množinu středů křivosti křivky.<br />
Evolventu křivky p získáme následujícím způsobem: Na křivce p zvolíme bod A, na<br />
křivce volíme další body, v každém bodě A 1 sestrojíme tečnu a naneseme na ni délku<br />
oblouku A 1 A. Takto získaný bod je bodem evolventy křivky p.<br />
Můžeme také říci, že jestliže odvalujeme přímku po křivce p, bod přímky opisuje<br />
evolventu.<br />
Na obrázku 2.10 je část evolventy kružnice. Křivka q je evolventou kružnice p (kruhovou<br />
evolventou). Kružnice p je evolutou křivky q.<br />
2.1.9 Řídící kuželová plocha<br />
Řídící kuželová plocha <strong>pro</strong>storové křivky je množina všech přímek, vedených pevným<br />
bodem V rovnoběžně se všemi tečnami křivky (tečna křivky je rovnoběžná s povrchovou
2.2. ŠROUBOVICE 27<br />
přímkou řídící kuželové plochy) (obr.2.11).<br />
Obrázek 2.11:<br />
2.2 Šroubovice<br />
2.2.1 Základní pojmy<br />
Definice 2. Šroubový pohyb vzniká složením rovnoměrného otáčivého pohybu kolem<br />
pevné přímky (osy) a rovnoměrného posuvného pohybu ve směru této přímky.<br />
Šroubovice je dráha bodu A při šroubovém pohybu, kde ω je úhel otočení a p posunutí<br />
bodu A (obr. 2.12).<br />
Výška závitu v je velikost posunutí bodu při otočení o 2π radiánů. Jestliže otočíme<br />
bod o 1 radián, označíme velikost posunutí v 0 a nazýváme redukovanou výškou závitu.<br />
Platí v 0 = v . 2π<br />
Šroubovice (o, A, v 0 , {±}) je určena osou o, bodem A, redukovanou výškou závitu v 0<br />
a informací o pravotočivosti nebo levotočivosti šroubovice (+ nebo −).<br />
Šroubovice leží na rotační válcové ploše. Jestliže rozvineme tuto válcovou plochu do<br />
roviny, šroubovice se rozvine do přímky. Pokud zavedeme souřadnicový systém tak, aby<br />
stopník šroubovice (bod, ve kterém šroubovice <strong>pro</strong>tíná půdorysnu) ležel v počátku a osa<br />
šroubovice byla rovnoběžná s osou y, je toto rozvinutí šroubovice grafem závislosti posunutí<br />
na délce oblouku (neboli úhlu otočení) (obr.2.13).<br />
2.2.2 Parametrické vyjádření šroubovice<br />
Parametrické rovnice pravotočivé šroubovice, jejíž osou je osa z, r je poloměr válcové<br />
plochy, na níž šroubovice leží, redukovaná výška závitu je v 0 a bod A[r, 0, 0], jsou<br />
x = r cos ω, y = r sin ω, z = v 0 ω, ω ∈ (0, 2π).<br />
Jestliže šroubovici umístíme tak, aby osa šroubovice byla kolmá na půdorysnu, pak<br />
půdorysem šroubovice je kružnice a nárysem šroubovice je zobecněná sinusoida (křivka<br />
odpovídající sinusoidě v afinitě).
2.2. ŠROUBOVICE 28<br />
Obrázek 2.12:<br />
Obrázek 2.13: Obrázek 2.14:<br />
2.2.3 Tečna šroubovice a její průvodní trojhran<br />
Věta 5. Tečny šroubovice svírají konstantní úhel s rovinou kolmou k ose šroubovice, resp.<br />
s osou šroubového pohybu. Říkáme, že šroubovice je křivka konstantního spádu.<br />
Důkaz: Určíme tečný vektor křivky a vypočteme odchylku tohoto vektoru od směrového<br />
vektoru osy šroubovice. Bez újmy na obecnosti předpokládejme, že osou šroubovice je<br />
osa z, tedy směrový vektor osy z = (0, 0, 1). Derivováním složek parametrické rovnice<br />
šroubovice podle parametru ω vypočteme<br />
Pro odchylku α vektorů z a P ′ platí<br />
P ′ = (−r sin ω, r cos ω, v 0 ).<br />
cos α = z · P ′<br />
|z| · |P ′ | = v 0<br />
1 · √r 2 + v 2 0<br />
=<br />
v<br />
√ 0<br />
.<br />
r2 + v0<br />
2<br />
Z toho je zřejmé, že úhel α nezávisí na parametru ω a tedy odchylka tečny šroubovice od<br />
její osy je ve všech bodech šroubovice stejná.
2.2. ŠROUBOVICE 29<br />
Půdorysné stopníky tečen šroubovice leží na kruhové evolventě kružnice, která je<br />
půdorysem šroubovice.<br />
Věta 6. Řídící kužel šroubovice (řídící kuželová plocha), který je tvořen površkami<br />
rovnoběžnými s tečnami šroubovice, je rotační, má výšku v 0 a poloměr podstavy r.<br />
Důkaz: Tvrzení plyne z důkazu věty 5. Tečna šroubovice je rovnoběžná s přeponou<br />
trojúhelníka o odvěsnách v 0 a r s tím, že odvěsna délky v 0 leží na ose šroubového pohybu.<br />
Hlavní normála šroubovice je normála kolmá k ose a osu <strong>pro</strong>tíná.<br />
Oskulační rovina je určena hlavní normálou a tečnou šroubovice.<br />
Binormála je normála kolmá na oskulační rovinu.<br />
2.2.4 Křivosti šroubovice<br />
Provedeme výpočet první a druhé křivosti šroubovice. Máme<br />
a vypočteme<br />
Určíme vektor<br />
P ′ = (−r sin ω, r cos ω, v 0 )<br />
P ′′ = (−r cos ω, −r sin ω, 0).<br />
q = P ′ × P ′′ = (rv 0 sin ω, −rv 0 cos ω, r 2 ).<br />
Pro první křivost podle věty 3 obdržíme<br />
√<br />
1 r<br />
k =<br />
2 v0 2 + r 4<br />
(r 2 + v 02 ) = r<br />
3 r 2 + v . 2 0<br />
První křivost šroubovice je tedy konstatní.<br />
Pro druhou křivost vypočteme<br />
2 k =<br />
v 0 r 2<br />
r 2 v 02 + r 4 = v 0<br />
r 2 + v 0<br />
2 .<br />
Tedy i druhá křivost šroubovice je konstatní.<br />
Provedený výpočet zřejmě nezáleží na orientaci šroubovice a ani na umístění osy.<br />
Věta 7.<br />
První křivost šroubovice je konstatní a platí<br />
1 k =<br />
r<br />
r 2 + v 0<br />
2 .<br />
Druhá křivost šroubovice je konstatní a platí<br />
2 k =<br />
v 0<br />
r 2 + v 0<br />
2 .<br />
Frenetův průvodní trojhran je tvořen tečnou, hlavní normálou a binormálou.
2.2. ŠROUBOVICE 30<br />
Obrázek 2.15: Obrázek 2.16:<br />
Poznámka 1.<br />
Šipkou budeme v půdorysu vyznačovat směr klesání šroubovice.<br />
Příklad 9. Sestrojíme průsečík šroubovice (o, A, v 0 , +) s rovinou α ‖ o - obr. 2.15.<br />
Řešení: (obr.2.16)<br />
1. Najdeme půdorys průsečíku A 1 šroubovice s rovinou α.<br />
2. Pomocí velikostí v 0 a r sestrojíme graf závislosti výšky na délce oblouku.<br />
3. Ze znalosti délky oblouku x = A 1 A 1 odečteme z grafu velikost výšky v x a tuto výšku<br />
naneseme od bodu A 2 ve směru stoupání. Na ordinále pak najdeme bod A 2 .<br />
□
2.2. ŠROUBOVICE 31<br />
Obrázek 2.17: Obrázek 2.18:<br />
Obrázek 2.19: Obrázek 2.20:
2.3. KONTROLNÍ OTÁZKY 32<br />
Příklad 10. Sestrojíme průsečík šroubovice (o, A, v 0 , +) s rovinou β ⊥ o - obr. 2.17.<br />
Řešení: (obr.2.18)<br />
1. V nárysu zjistíme vzdálenost v x bodu A šroubovice od roviny β.<br />
2. Pomocí velikostí v 0 a r sestrojíme graf závislosti výšky na délce oblouku.<br />
3. Ze znalosti změny výšky, o kterou musí vystoupat bod A, odečteme z grafu délku<br />
oblouku x, tento oblouk naneseme od bodu A 1 ve směru stoupání. Na ordinále pak<br />
najdeme v rovině β bod A (rozumí se jeho nárys).<br />
Příklad 11. Sestrojíme tečnu šroubovice (o, A, v 0 , +) v bodě A - obr. 2.19.<br />
Řešení: (obr.2.20)<br />
1. Určíme půdorys t 1 tečny t v bodě A.<br />
2. Sestrojíme půdorys površky t řídícího kužele, která je rovnoběžná s tečnou (její<br />
stopník najdeme na půdorysu šroubovice o úhel 90 o ve směru klesání od bodu A).<br />
3. Odvodíme nárys P 2 stopníku P a nárys površky t.<br />
4. Tečna <strong>pro</strong>chází bodem A a je rovnoběžná s t.<br />
□<br />
□<br />
2.3 Kontrolní otázky<br />
2.1 Definujte hlavní normálu <strong>pro</strong>storové křivky.<br />
2.2 Definujte řídící kuželovou plochu <strong>pro</strong>storové křivky.<br />
2.3 Jakou první a druhou křivost má přímka?<br />
2.4 Jakou první a druhou křivost má kružnice?<br />
2.5 Uved’te definici šroubového pohybu.<br />
2.6<br />
Čím je určen šroubový pohyb?<br />
2.7 Definujete parametr v 0 šroubového pohybu?<br />
2.8 Uved’te vztah mezi výškou závitu šroubovice a redukovanou výškou závitu.<br />
2.9 Definujte (dvěma způsoby) evolutu křivky a přibližně načrtněte evolutu elipsy.
Kapitola 3<br />
Obecné poznatky o plochách<br />
3.1 Základní pojmy<br />
Plocha je<br />
• jednoparametrická soustava křivek (plocha vzniká pohybem křivky, která není dráhou<br />
pohybu - křivka se může během pohybu měnit)<br />
• dvouparametrická soustava bodů<br />
Obrázek 3.1: Obrázek 3.2:<br />
Podobně jako u křivek nyní uvedeme ”<br />
matematickou“ definici plochy. Používáme zde<br />
značení parametrů, které vychází z tenzorové symboliky. V dalším textu budeme ale <strong>pro</strong><br />
jednoduchost místo parametrů u 1 , u 2 používat označení u, v:<br />
Definice 3. Regulární plochou třídy C n v E 3 rozumíme množinu P ⊂ E 3 , <strong>pro</strong> niž existuje<br />
vektorová funkce P (u 1 , u 2 ), (u 1 , u 2 ) ⊂ Ω, kde Ω je oblast (otevřená kompaktní množina),<br />
taková že<br />
(a) P : Ω → P je zobrazení na množinu,<br />
(b) P je třídy C n (n ≥ 3),<br />
(c) ∂P<br />
∂u 1<br />
a ∂P<br />
∂u 2 jsou lineárně nezávislé ve všech bodech oblasti Ω,<br />
33
3.1. ZÁKLADNÍ POJMY 34<br />
(d) (u 1 0, u 2 0) ∈ Ω,(u 1 1, u 2 1) ∈ Ω a (u 1 0, u 2 0) ≠ (u 1 1, u 2 1) ⇒ P (u 1 0, u 2 0) ≠ P (u 1 1, u 2 1).<br />
Klasifikace ploch<br />
Plocha vzniká pohybem křivky, <strong>pro</strong>to nás zajímají dva způsoby klasifikace ploch: podle<br />
druhu pohybu a podle tvořící křivky. V následujících dvou tabulkách jsme plochy<br />
roztřídili podle těchto dvou hledisek.<br />
Podle druhu pohybu<br />
Název Pohyb Příklad<br />
translační posunutí válec, rovina<br />
rotační rotace rot. válec, rot. kužel, rot. hyperboloid<br />
šroubové šroubový pohyb cyklická šroubová plocha, vývrtková plocha<br />
Podle tvořící křivky<br />
Název Křivka Příklad<br />
přímkové přímka kuželová plocha, hyperbolický paraboloid<br />
cyklické kružnice válec, Archimédova serpentina<br />
jiné jiná křivka kvadriky, obalové, grafické<br />
Rovnice plochy<br />
• Parametrické vyjádření:<br />
x = x(u, v), y = y(u, v), z = z(u, v), u ∈ I, v ∈ J<br />
(např. parametrické vyjádření rotační válcové plochy je x = 3 cos u, y = 3 sin u, z =<br />
v, u ∈ 〈0, 2π〉, v ∈ R<br />
nebo zápis pomocí vektorové funkce: r(u, v) = (x(u, v), y(u, v), z(u, v))<br />
jestliže u = konst. dostáváme:<br />
x = x(u 0 , v), y = y(u 0 , v), z = z(u 0 , v) v-křivky, (<strong>pro</strong> uvedený válec jsou v-<br />
křivkami přímky)<br />
jestliže v = konst. dostáváme:
3.2. ÚLOHY NA PLOCHÁCH 35<br />
x = x(u, v 0 ), y = y(u, v 0 ), z = z(u, v 0 ) u-křivky, (<strong>pro</strong> uvedený válec jsou u-<br />
křivkami kružnice)<br />
• Explicitní tvar: z = f(x, y) (např. z = 3x + 7y − 9)<br />
• Implicitní vyjádření: F (x, y, z) = 0 (např. 3x 2 + y 2 + 4z − 2x = 0)<br />
Křivka na ploše je křivka, jejíž body vyhovují rovnici plochy. Speciálními křivkami<br />
na ploše jsou parametrické křivky. Jsou charakterizovány tím, že jeden z parametrů je<br />
konstantní.<br />
Tečná rovina plochy je množina tečen křivek plochy v daném bodě. Tečna plochy<br />
je přímka tečné roviny, která <strong>pro</strong>chází dotykovým bodem.<br />
Normála plochy je kolmice k tečné rovině plochy v bodě dotyku. Dvě plochy se<br />
dotýkají v daném bodě, jestliže v něm mají společnou tečnou rovinu.<br />
Průniková křivka je množina společných bodů dvou ploch.<br />
Bod na ploše je regulární, jestliže v něm existuje právě jedna tečná rovina a singulární<br />
v ostatních případech.<br />
Přímky na ploše rozdělujeme na regulární, kdy v každém bodě přímky existuje jiná<br />
tečná rovina - tečné roviny tvoří svazek rovin (např. přímky na rotačním jednodílném<br />
hyperboloidu) a torzální, kdy existuje jediná tečná rovina podél celé přímky (např.<br />
přímky na kuželové ploše).<br />
3.2 Úlohy na plochách<br />
• Tečná rovina τ v bodě T a normála plochy:<br />
1. zvolíme dvě křivky k 1 , k 2 na ploše <strong>pro</strong>cházející bodem T (vhodné jsou např.<br />
tvořící křivka a dráha pohybu, při řešení úlohy výpočtem pak je vhodné zejména<br />
parametrické křivky),<br />
2. určíme tečny t 1 a t 2 k těmto křivkám (předpokládáme, že jsou různé),<br />
3. tečná rovina τ je určena tečnami t 1 a t 2 (obr. 3.2),<br />
4. normálu plochy určíme jako kolmici k tečné rovině v daném bodě.<br />
• Řez plochy rovinou ϱ a tečna řezu:<br />
1. zvolíme křivku k plochy<br />
2. průnikem křivky k s rovinou ϱ je bod K (jeden bod řezu)<br />
3. opakováním bodů 1) a 2) dostáváme jednotlivé body řezu (obr. 3.3).<br />
4. tečna řezu je průsečnicí tečné roviny a roviny řezu (obr. 3.4).<br />
• Průsečík přímky p s plochou κ:<br />
1. <strong>pro</strong>ložíme rovinu ϱ přímkou p,
3.2. ÚLOHY NA PLOCHÁCH 36<br />
Obrázek 3.3: Obrázek 3.4:<br />
2. určíme řez plochy κ rovinou ϱ, dostaneme průnikovou křivku k,<br />
3. průnik přímky p a křivky k je hledaný průsečík X (obr. 3.5).<br />
Obrázek 3.5: Obrázek 3.6:<br />
• Průnik dvou ploch α a β:<br />
1. zvolíme pomocnou rovinu ϱ,<br />
2. najdeme průnikovou křivku k 1 roviny ϱ s plochou α,<br />
3. najdeme průnikovou křivku k 2 roviny ϱ s plochou β,<br />
4. průsečík P křivek k 1 a k 2 je bodem průniku ploch α a β (obr. 3.6),<br />
5. opakováním bodů 1)-4) najdeme požadovaný počet bodů průniku ploch α a β,<br />
6. tečna průnikové křivky v daném bodě je průsečnicí tečných rovin obou ploch v<br />
daném bodě (jiná možnost určení tečny průnikové křivky spočívá v konstrukci<br />
kolmice k rovině dané normálami daných ploch v daném bodě).<br />
Skutečný obrys plochy tvoří body plochy, v nichž jsou <strong>pro</strong>mítací přímky tečnami<br />
plochy. Zdánlivý obrys plochy je průmět skutečného obrysu plochy.
3.3. VÝPOČETNÍ ŘEŠENÍ NĚKTERÝCH ÚLOH NA PLOCHÁCH 37<br />
3.3 Výpočetní řešení některých úloh na plochách<br />
Uved’me některé důležité věty z diferenciální geometrie ploch.<br />
Věta 8. Všechny tečny regulárních křivek na regulární ploše v daném bodě leží v jedné<br />
rovině.<br />
Důkaz: Uvažujme křivku ( u(t), v(t) ) na ploše P ( u, v ) . Určíme<br />
dP<br />
dt = ∂P<br />
∂u · du<br />
dt + ∂P<br />
∂v · dv<br />
dt = P 1 · du<br />
dt + P 2 · dv<br />
dt .<br />
Tedy každý tečný vektor je lineární kombinací nekolineárních vektorů P 1 a P 2 .<br />
Na základě této věty můžeme stanovit rovnici tečné roviny plochy dané parametrickým<br />
(nebo vektorovým) vyjádřením tak, že určíme tečné vektory parametrických křivek pomocí<br />
parciálního derivování. Tyto vektory tvoří zaměření tečné roviny. Normálu plochy<br />
pak vypočteme pomocí operace vektorového násobení.<br />
Příklad 12. Pro plochu danou vektorovým vyjádřením<br />
P (u, v) = (u 2 cos v, u 2 sin v, u) , u ∈ (0, +∞) , v ∈ (0, 2π) .<br />
určete v obecném bodě tečnou rovinu a normálu.<br />
Řešení: Pomocí parciálního derivování určíme tečné vektory parametrických křivek:<br />
P 1 (u, v) = ∂P<br />
∂u<br />
= (2u cos v, 2u sin v, 1) ,<br />
P 2 (u, v) = ∂P<br />
∂v = (−u2 sin v, u 2 cos v, 0) ,<br />
n(u, v) = P 1 × P 2 = (−u 2 cos v, −u 2 sin v, 2u 3 ) .<br />
Tečná rovina v daném bodě A je určena uvedenými tečnými vektory. Normála je<br />
pak určena daným bodem vektorem normály. Obecně lze tedy tečnou rovinu vyjádřit ve<br />
vektorovém tvaru<br />
X(α, β) = A + αP 1 + βP 2 , α ∈ R , β ∈ R .<br />
Vektorový popis normály v daném bodě A je tvaru<br />
Y (γ) = A + γn , γ ∈ R .<br />
Zadanou plochou je rotační paraboloid, který vzniká rotací paraboly z = x okolo<br />
osy z. Parametrickými křivkami jsou jednotlivé polohy rotující paraboly a rovnoběžkové<br />
kružnice.<br />
□<br />
Věta 9. Necht’ je plocha dána implicitním vyjádřením f(x 1 , x 2 , x 3 ) = 0. Pak jejím normálovým<br />
vektorem (v daném bodě) je vektor n = (f 1 , f 2 , f 3 ), jehož složky jsou dány parciálními<br />
derivacemi funkce f.
3.4. GAUSSOVA KŘIVOST PLOCHY 38<br />
Příklad 13. Pro plochu danou implicitním vyjádřením<br />
f(x, y, z) = x 2 + y 2 − z = 0 .<br />
určete v bodě X[1, 1, 2] tečnou rovinu a normálu.<br />
Řešení: Pomocí věty 9 stanovíme vektor normály plochy v daném bodě:<br />
n = ( ∂f<br />
∂x<br />
(1, 1, 2),<br />
∂f<br />
∂y<br />
∂f<br />
(1, 1, 2), (1, 1, 2)) = (2, 2, −1) .<br />
∂z<br />
Tečná rovina je pak určena bodem X a svým normálovým vektorem, tj. normálovým<br />
vektorem plochy. Tečná rovina má tedy rovnici (absolutní člen vyjde nulový)<br />
2x + 2y − z = 0 .<br />
Poznamenejme, že jde o rotační kuželovou plochu s vrcholem v počátku souřadnicového<br />
systému a s osou v ose z.<br />
□<br />
3.4 Gaussova křivost plochy<br />
V bodě X plochy uvažujme normálu n a touto normálou <strong>pro</strong>ložme svazek rovin. Každá<br />
z rovin tohoto svazku vytváří na ploše řez. Uvažujme orientovanou první křivost těchto<br />
řezů (nazýváme je normálové řezy) a označme k max , resp. k min , největší, resp. nejmenší,<br />
z hodnot, kterých orientované křivosti nabývají.<br />
Pokud není hodnota první křivosti <strong>pro</strong> všechny normálové křivosti stejná, pak řezy,<br />
<strong>pro</strong> které dostaneme extrémní první křivosti, leží v rovinách na sebe kolmých.<br />
Gaussovou křivostí v bodě plochy rozumíme číslo G = k max · k min .<br />
3.5 Parametrické vyjádření ploch<br />
Nyní se vrátíme k otázce parametrizace ploch, které vznikají pohybem křivky. Jestliže v<br />
transformační matici existuje jeden parametr, může matice popisovat pohyb. Příkladem<br />
je rotace nebo šroubový pohyb, kde parametrem bude úhel otočení.<br />
Uvažujme <strong>pro</strong>storovou křivku<br />
Y (v) = (x(v), y(v), z(v)), v ∈ I v . (3.1)<br />
a matici T transformace (např. rotace nebo šroubového pohybu, ale může jít i o jiný pohyb).<br />
Parametr pohybu označme u, tedy matice transformace se stává maticovým popisem<br />
pohybu a značíme ji T(u). Parametrické vyjádření plochy, která vznikne daným pohybem<br />
dané křivky, pak můžeme snadno zapsat ve tvaru<br />
P h (u, v) = Y h (v)T(u) , v ∈ I v , u ∈ I u , (3.2)<br />
kde P h (u, v) = [x(u, v), y(u, v), z(u, v), 1] a Y h (v) = [x(v), y(v), z(v), 1] je vyjádření bodu<br />
na ploše a bodu na křivce v homogenních souřadnicích.
3.5. PARAMETRICKÉ VYJÁDŘENÍ PLOCH 39<br />
Pomocí vztahu (3.2) odvodíme parametrické vyjádření rotační plochy, která vzniká<br />
rotaci dané (obecně <strong>pro</strong>storové) křivky okolo osy z. Platí<br />
⎛<br />
⎞<br />
cos u, sin u, 0, 0<br />
P h (u, v) = [x(v), y(v), z(v), 1] · ⎜ − sin u, cos u, 0, 0<br />
⎟<br />
⎝ 0, 0, 1, 0 ⎠ , v ∈ I v, u ∈ I u . (3.3)<br />
0, 0, 0, 1<br />
Snadno dostaneme po vynechání homogenizující složky parametrické rovnice rotační<br />
plochy, že platí<br />
P (u, v) = (x(v) cos u − y(v) sin u, x(v) sin u + y(v) cos u, z(v)) , u ∈ I u , v ∈ I v , (3.4)<br />
což je vyjádření, které jsme uvedli v kapitole o rotačních plochách na straně 42 – rovnice<br />
(4.3).<br />
Podobně je možné odvodit parametrické vyjádření šroubové plochy, která vzniká pohybem<br />
dané <strong>pro</strong>storové křivky a která má osu v ose z, je dáno v 0 a uvádíme obě možnosti<br />
orientace šroubového pohybu (znaménko plus <strong>pro</strong> kladnou orientaci, znaménko minus <strong>pro</strong><br />
zápornou orientaci):<br />
P h (u, v) = [x(v), y(v), z(v), 1] ·<br />
⎛<br />
⎜<br />
⎝<br />
cos u, sin u, 0, 0<br />
− sin u, cos u, 0, 0<br />
0, 0, 1, 0<br />
0, 0, ±v 0 u, 1<br />
⎞<br />
⎟<br />
⎠ , v ∈ I v, u ∈ I u . (3.5)<br />
Po vynechání homogenizující složky parametrické rovnice šroubové plochy dostaneme<br />
P (u, v) = (x(v) cos u−y(v) sin u, x(v) sin u+y(v) cos u, z(v)±v 0 u) , u ∈ I u , v ∈ I v , (3.6)<br />
což je vyjádření, které jsme uvedli v kapitole o šroubových plochách na straně 51 – rovnice<br />
(5.3).<br />
Použití transformací <strong>pro</strong> odvození rovnic ploch ale dovoluje podstatně více. Je možné<br />
použít např. rotaci okolo jiné souřadnicové osy nebo okolo osy obecně umístěné. Podobně<br />
je možné postupovat u šroubových ploch. Tvořící křivka může při daném pohybu podléhat<br />
i tvarové změně v závislosti na pohybovém parametru, čímž vznikají objekty, kterými<br />
se v tomto textu nezabýváme, ale které jsou využívány v kategorii “sweep” moderních<br />
CAD/CAM systémů.<br />
Příklad 14. Uved’me, jakou Gaussovu křivost mají některé plochy:<br />
• Rovina má ve všech bodech nulovou Gaussovu křivost, nebot’ normálovými řezy jsou<br />
přimky a tedy k max = k min = 0.<br />
• Normálovými řezy na kulové ploše jsou kružnice se středem ve středu kulové plochy.<br />
Jejich křivost je 1 , kde r je poloměr kulové plochy. Tedy <strong>pro</strong> kulovou plochu platí,<br />
r<br />
že ve všech bodech G = 1 .<br />
r 2<br />
• Na rotační válcové ploše jsou normálovými řezy s extrémní křivostí površka a<br />
rovnoběžková kružnice, tedy k max = 1 a k r min = 0. V libovolném bodě rotační<br />
válcové plochy tedy G = 1 · 0 = 0. Roviny normálových řezů <strong>pro</strong> uvedené dvě<br />
r<br />
extrémní křivosti jsou na sebe kolmé.
3.6. KONTROLNÍ OTÁZKY 40<br />
• Anuloidem (kruhovým prstencem) rozumíme rotační plochu, která vznikne rotací<br />
kružnice okolo osy ležící v rovině této kružnice. Necht’ osová kružnice anuloidu, tj.<br />
kružnice, po které se pohybuje při rotaci střed kružnice, má poloměr a a necht’<br />
rotující kružnice má poloměr r, r < a. Pro Gaussovu křivost v bodech anuloidu,<br />
které leží nejblíže ose, máme (není ale jasné, která z těchto křivostí je menší, <strong>pro</strong>to<br />
uvedené označení)<br />
k 1 = 1 r , k 2 = 1<br />
a − r , G = − 1<br />
r(a − r) .<br />
Gaussova křivost je v tomto případě záporná, nebot’ orientace uvedených křivostí je<br />
opačná, tj. středy uvedených dvou kružnic leží na opačných částech (polopřímkách)<br />
normály.<br />
3.6 Kontrolní otázky<br />
3.1 Popište, jak lze obecně určit tečnou rovinu a normálu plochu.<br />
3.2 Popište, jak lze určit tečnou rovinu a normálu plochu z parametrických rovnic plochy.<br />
3.3 Popište, jak lze zkonstruovat tečnu řezu plochy.<br />
3.4 Uved’te dva způsoby určení tečny průnikové křivky dvou ploch (návod: pomocí<br />
tečných rovin nebo pomocí normál ploch).
Kapitola 4<br />
Rotační plochy<br />
4.1 Základní pojmy<br />
Rotační plocha vzniká rotací křivky k kolem přímky o. Předpokládáme, že křivka k<br />
nesplývá s přímkou o a neleží v rovině kolmé na přímku o (obr. 4.1, 4.2). Při řešení úloh<br />
v Mongeově <strong>pro</strong>mítání budeme volit osu o zpravidla kolmou k půdorysně.<br />
Křivku k nazýváme tvořící křivka rotační plochy, přímku o osou rotační plochy.<br />
Obrázek 4.1: Obrázek 4.2:<br />
Rovnoběžková kružnice (rovnoběžka) r A je kružnice, která vznikne rotací libovolného<br />
bodu A tvořící křivky kolem osy o.<br />
Meridián (poledník) je řez rotační plochy rovinou, <strong>pro</strong>cházející osou rotační plochy;<br />
hlavní meridián m je meridián ležící v rovině rovnoběžné s průmětnou.<br />
Tečnou rovinu rotační plochy určujeme tečnami dvou křivek plochy <strong>pro</strong>cházejících<br />
daným bodem. Obvykle je tečná rovina určena bud’ tečnou meridiánu (t m ) a tečnou<br />
rovnoběžkové kružnice (t r ), nebo tečnou tvořící křivky (t k ) a tečnou rovnoběžkové kružnice<br />
(t r ).<br />
Normála n rotační plochy je kolmice na tečnou rovinu v bodě dotyku.<br />
41
4.2. PARAMETRICKÉ VYJÁDŘENÍ ROTAČNÍ PLOCHY 42<br />
4.2 Parametrické vyjádření rotační plochy<br />
Rotační plocha vznikne otáčením tzv. tvořící křivky k kolem osy o. Necht’ osou otáčení o<br />
je souřadnicová osa z a křivka k je dána vektorovou funkcí Y (v), v ∈ I v (obr. 4.3).<br />
Obrázek 4.3:<br />
Pro křivku k označme složky její vektorové rovnice<br />
Y (v) = (x(v), y(v), z(v)), v ∈ I v . (4.1)<br />
Trajektorií bodu Y (v) křivky k je kružnice, která leží v rovině kolmé k o = z. Tato<br />
kružnice má střed S na ose o a její poloměr je roven r(v) = |SY (v)| = √ [x(v)] 2 + [y(v)] 2 .<br />
Pro polohový vektor bodu X rotační plochy platí<br />
X(u, v) = (r(v) cos u, r(v) sin u, z(v)) , (4.2)<br />
kde <strong>pro</strong> parametry u, v platí u ∈ 〈0, 2π) a v ∈ I v . Tak jsme odvodili vektorovou rovnici<br />
rotační plochy, která vznikne rotací křivky k (může být i <strong>pro</strong>storová).<br />
Stanovení parametrického vyjádření rotační plochy lze ale <strong>pro</strong>vést také obecným postupem<br />
pomocí transformační matice – viz str. 38. Tak snadno odvodíme odvodíme i jiný<br />
tvar rovnice rotační plochy:<br />
X(u, v) = (x(v) cos u − y(v) sin u, x(v) sin u + y(v) cos u, z(v)) , u ∈ R , v ∈ I v . (4.3)<br />
Rozdíl v uvedených dvou tvarech parametrického popisu rotační plochy je patrný<br />
při studiu parametrických křivek. Jedním systémem parametrických křivek jsou v obou<br />
případech rovnoběžkové kružnice. Druhým systémem parametrických křivek jsou v případě<br />
(4.2) polomeridiány dané rotační plochy. Pokud použijeme vyjádření (4.3), je druhý<br />
systém parametrických křivek tvořen polohami tvořící křivky při daném pohybu.
4.3. VLASTNOSTI ROTAČNÍCH PLOCH 43<br />
Příklad 15. Určíme parametrické vyjádření rotační plochy, která vznikne rotací přímky<br />
Y (v) = (1 − v, 5v, 5v) kolem osy z. Dále určíme tečnou rovinu a normálu plochy v bodě<br />
A = [1; 0; 0].<br />
Řešení: Vyjdeme ze vztahu (4.2). Poloměr trajektorie bodu je r(v) = √ (1 − v) 2 + (5v) 2 =<br />
√<br />
1 − 2v + 26v2 . Plochou je jednodílný rotační hyperboloid a vektorová rovnice plochy je<br />
X(u, v) = ( √ 1 − 2v + 26v 2 cos u, √ 1 − 2v + 26v 2 sin u, 5v), u ∈ 〈0, 2π), v ∈ R.<br />
P 1 (u, v) = ∂P<br />
∂u = (−√ 1 − 2v + 26v 2 sin u, √ 1 − 2v + 26v 2 cos u, 0)<br />
P 2 (u, v) = ∂P<br />
∂v = ( −2 + 52v<br />
2 √ 1 − 2v + 26v cos u, −2 + 52v<br />
2 2 √ sin u, 5).<br />
1 − 2v + 26v2 Bod A = [1; 0; 0] získáme volbou parametrů u = 0, v = 0, dosadíme tyto hodnoty<br />
do vypočtených parciálních derivací a dostaneme dva vektory ze zaměření tečné roviny<br />
P 1 (0, 0) = (0, 1, 0), P 2 (0, 0) = (−1, 0, 5). Normálový vektor roviny vypočteme pomocí<br />
vektorového součinu<br />
n = P 1 (0, 0) × P 2 (0, 0) = (0, 1, 0) × (−1, 0, 5) = (5, 0, 1).<br />
Rovnice tečné roviny po dopočítání absolutního členu je 5x + z − 5 = 0 a vektorová<br />
rovnice normály n(t) = (1 + 5t, 0, t), t ∈ R.<br />
□<br />
4.3 Vlastnosti rotačních ploch<br />
• Rotační plocha je souměrná podle své osy a podle roviny každého meridiánu.<br />
• Tečná rovina rotační plochy je kolmá k rovině meridiánu <strong>pro</strong>cházející dotykovým<br />
bodem.<br />
• Tečné roviny rotační plochy v bodech téže rovnoběžkové kružnice obalují bud’<br />
rotační kuželovou plochu, nebo rotační válcovou plochu nebo rovinu.<br />
• Tečny meridiánu v bodech téže rovnoběžkové kružnice tvoří bud’ rotační kuželovou<br />
plochu, nebo rotační válcovou plochu nebo rovinu (obr. 4.4, 4.5).<br />
• Normála rotační plochy <strong>pro</strong>tíná osu nebo je s ní rovnoběžná.<br />
• Normály rotační plochy v bodech téže rovnoběžkové kružnice tvoří bud’ rotační<br />
kuželovou plochu, nebo rotační válcovou plochu nebo rovinu.<br />
Rovnoběžková kružnice se nazývá<br />
hrdlo, jestliže tečny podél této rovnoběžky tvoří rotační válcovou plochu a poloměr<br />
je lokálním minimem, tj. ze všech okolních rovnoběžek je tento poloměr nejmenší,<br />
rovník, jestliže tečny podél této rovnoběžky tvoří rotační válcovou plochu a poloměr<br />
je lokálním maximem, tj. ze všech okolních rovnoběžek je tento poloměr největší,<br />
kráter, jestliže tečny podél této rovnoběžky tvoří rovinu.
4.4. KLASIFIKACE ROTAČNÍCH PLOCH 44<br />
2,5<br />
2,5<br />
2<br />
2<br />
1,5<br />
1,5<br />
1<br />
1<br />
1<br />
-1<br />
0,5<br />
-0,5<br />
0,5<br />
00<br />
0<br />
-0,5<br />
0,5<br />
-1<br />
1<br />
0,5<br />
0<br />
-1 -0,5 0<br />
0,5<br />
1<br />
Obrázek 4.4:<br />
Obrázek 4.5:<br />
Skutečným obrysem rotační plochy při pravoúhlém <strong>pro</strong>mítání na rovinu rovnoběžnou s<br />
osou je hlavní meridián a hraniční kružnice plochy. V případě kolmého průmětu na rovinu<br />
kolmou k ose jsou skutečným obrysem hrdelní, rovníkové a hraniční kružnice plochy.<br />
Zdánlivým obrysem rotační plochy je průmět skutečného obrysu.<br />
4.4 Klasifikace rotačních ploch<br />
Podle typu tvořící křivky dělíme rotační plochy následovně:<br />
Název Tvořící křivka Rotační plocha<br />
Přímkové přímka p ‖ o válcová<br />
přímka p různoběžná s o<br />
kuželová<br />
přímka p mimoběžná s o<br />
jednodílný rotační hyperboloid<br />
Cyklické kružnice k ⊂ β, o ⊂ β anuloid<br />
kružnice k ⊂ β, o ⊄ β<br />
globoid<br />
kružnice k ⊂ β, o ⊂ β a S ∈ o kulová plocha<br />
Rotační elipsa e ⊂ β, o ⊂ β rotační elipsoid<br />
kvadriky parabola p ⊂ β, o ⊂ β rotační paraboloid<br />
hyperbola (rotace okolo vedlejší osy) jednodílný rotační hyperboloid<br />
hyperbola (rotace okolo hlavní osy) dvojdílný rotační hyperboloid<br />
Obecné<br />
4.5 Úlohy na rotačních plochách<br />
Příklad 16. Rotační plocha je dána osou o a tvořící křivkou k. Sestrojte tečnou rovinu<br />
v bodě M ∈ k - obr. 4.6.
o 2<br />
A 2<br />
r A2<br />
k 2<br />
4.5. ÚLOHY NA ROTAČNÍCH PLOCHÁCH 45<br />
m 2<br />
A 1<br />
k 1<br />
o 1<br />
S 2<br />
x12<br />
m 1<br />
r A1<br />
M 2<br />
M 2<br />
r M2<br />
k 2<br />
o 2<br />
k 2<br />
o 2<br />
t´ 2<br />
t 2<br />
t 1<br />
k 1<br />
o 1<br />
x 12<br />
M 1<br />
t´ 1<br />
k 1<br />
o 1<br />
x 12<br />
M 1<br />
r M1<br />
Obrázek 4.6:<br />
Obrázek 4.7:<br />
Řešení: (obr. 4.7)<br />
1. Sestrojíme nárys a půdorys rovnoběžkové kružnice r <strong>pro</strong>cházející bodem M.<br />
2. Sestrojíme v bodě M tečnu t k rovnoběžkové kružnici.<br />
3. Sestrojíme v bodě M tečnu t ′ ke křivce k.<br />
4. Tečná rovina τ je určena tečnami t a t ′ .<br />
Příklad 17. Rotační plocha je dána osou o a hlavním meridiánem m. Sestrojíme tečnou<br />
rovinu plochy v bodě M ∈ k, je-li dáno M 2 - obr. 4.8.<br />
Řešení: (obr. 4.9)<br />
1. Sestrojíme nárys a půdorys rovnoběžkové kružnice r <strong>pro</strong>cházející bodem M a odvodíme<br />
půdorys bodu M.<br />
2. Sestrojíme v bodě M tečnu t k rovnoběžkové kružnici.<br />
3. Najdeme bod M hlavního meridiánu, ležící na stejné rovnoběžkové kružnici jako<br />
bod M.<br />
4. Sestrojíme v bodě M tečnu t M k meridiánu.<br />
5. Použitím vlastnosti, že tečny meridiánu v bodech téže rovnoběžkové kružnice se<br />
<strong>pro</strong>tínají na ose, sestrojíme tečnu t ′ meridiánu v bodě M.<br />
6. Tečná rovina τ je určena tečnami t a t ′ .<br />
□<br />
Důležitou úlohu představuje určení řezu rotační plochy rovinou ρ. Použijeme obecný<br />
postup z úvodní kapitoly o plochách, ale <strong>pro</strong>vedeme modifikaci <strong>pro</strong> rotační plochy. Nejprve<br />
najdeme vhodnou křivku na ploše. Touto vhodnou křivkou je na rotační ploše<br />
rovnoběžková kružnice, kterou dostaneme jako řez pomocnou rovinou kolmou na osu<br />
rotační plochy. Tuto rovinu využijeme i při hledání průsečíků křivky s rovinou ρ.<br />
□
4.5. ÚLOHY NA ROTAČNÍCH PLOCHÁCH 46<br />
m 2<br />
o 2<br />
m 2<br />
o 2<br />
t´ 2<br />
M 2<br />
M 2<br />
r M2<br />
M 2<br />
t 2<br />
m 1<br />
o 1<br />
x 12<br />
m 1<br />
o 1<br />
x 12<br />
M 1<br />
r M1<br />
M 1<br />
t´ 1<br />
t 1<br />
Obrázek 4.8:<br />
Obrázek 4.9:<br />
Příklad 18. Rotační plocha je dána osou o a meridiánem m. Sestrojíme řez rotační plochy<br />
rovinou ρ, která je určena stopami - obr. 4.10.<br />
Řešení: (obr. 4.11)<br />
1. Zvolíme pomocnou rovinu α kolmou k ose o rotační plochy. V nárysu se tato rovina<br />
<strong>pro</strong>mítne do přímky kolmé k ose o.<br />
2. Sestrojíme průnik roviny α s rotační plochou. Průnikem je rovnoběžková kružnice<br />
k α , jejíž poloměr najdeme v nárysu ve skutečné velikosti (je to vzdálenost průsečíku<br />
roviny α s meridiánem od osy). Nárysem této kružnice je úsečka, půdorysem kružnice.<br />
3. Určíme průnik roviny α s rovinou ρ. Průnikem je hlavní přímka h α roviny ρ, odvodíme<br />
ji do půdorysu.<br />
4. v půdoryse najdeme průsečíky A, A hlavní přímky h α s rovnoběžkovou kružnicí k α .<br />
Tyto body jsou zároveň průsečíky kružnice k α s rovinou ρ. Z půdorysu je odvodíme<br />
na hlavní přímku h α do nárysu.<br />
5. Body A, A jsou dva body řezu rotační plochy rovinou ρ.<br />
6. Postup opakujeme volbou další roviny kolmé k ose. Na obr. 4.11 jsou sestrojeny<br />
čtyři body průniku roviny ϱ s touto plochou. Body A, A jsme sestrojili v pomocné<br />
rovině α (α ⊥ o), body B, B v pomocné rovině β (β ⊥ o). Tímto způsobem najdeme<br />
dostatečný počet bodů, kterými pak <strong>pro</strong>ložíme křivku řezu.<br />
Poznámka 2. Jestliže je rotační plochou rotační kvadrika, je řezem kuželosečka. V tomto<br />
případě můžeme řez sestrojit přesněji.<br />
□
4.6.<br />
PRŮNIKY ROTAČNÍCH PLOCH 47<br />
Obrázek 4.10: Obrázek 4.11:<br />
4.6 Průniky rotačních ploch<br />
Použijeme algoritmus <strong>pro</strong> určení průniku ploch, pouze použijeme speciální typ plochy ϱ<br />
<strong>pro</strong> jednotlivé vzájemné polohy (obr. 4.12).<br />
a) Pokud osy rotačních ploch splývají, jsou průnikovými křivkami společné rovnoběžkové<br />
kružnice.<br />
b) Pokud jsou osy rotačních ploch rovnoběžné, volíme jako plochu ϱ rovinu kolmou na<br />
osy.<br />
c) Pokud jsou osy rotačních ploch různoběžné, volíme jako plochu ϱ kulovou plochu se<br />
středem v průsečíku os.<br />
d) Pokud jsou osy rotačních ploch mimoběžné, použijeme obecný algoritmus.<br />
4.7 Rotační kvadriky<br />
• singulární (vzniknou rotací singulární kuželosečky)<br />
a) rotační válcová plocha x2 + y2<br />
= 1<br />
a 2 a 2<br />
b) rotační kuželová plocha x2 + y2<br />
− z2 = 0<br />
a 2 a 2 c 2<br />
• regulární (vzniknou rotací regulární kuželosečky)<br />
a) kulová plocha x 2 + y 2 + z 2 = r 2
4.8. CVIČENÍ 48<br />
b) elipsoid x2 + y2<br />
+ z2 = 1<br />
a 2 a 2 c 2<br />
b) paraboloid x2<br />
2p + y2<br />
2q ± z = 0<br />
b) hyperboloid<br />
Obrázek 4.12:<br />
jednodílný x2 + y2<br />
− z2 = 1<br />
a 2 a 2 c 2<br />
dvojdílný − x2<br />
a 2<br />
− y2<br />
a 2 z 2<br />
c 2 = 1<br />
Řezem rotační kvadriky je kuželosečka.<br />
Konstrukce řezu:<br />
- najít 5 prvků (5 bodů, 3 body a 2 tečny ve dvou z nich, apod.) a použít Pascalovu<br />
větu<br />
- nebo v konkrétních případech najít určující prvky řezu (např. hlavní osy elipsy).<br />
Průnikem rotačních kvadrik je křivka 4. stupně.<br />
Věta 10. Průnik dvou rotačních kvadrik se rozpadne na dvě kuželosečky právě tehdy, když<br />
existuje kulová plocha současně vepsaná oběma kvadrikám.<br />
4.8 Cvičení<br />
4.1 Sestavte parametrické rovnice plochy, která vznikne rotací obecné přímky okolo osy.<br />
(Návod: za osu rotace zvolte souřadnicovou osu.)<br />
4.2 Sestavte parametrické rovnice anuloidu. (Návod: za osu anuloidu zvolte souřadnicovou<br />
osu.)<br />
4.3 Rozhodněte, jaká plocha je popsána parametrickým vyjádřením:<br />
x = a cos u cos v , y = a cos u cos v , z = b sin u , u ∈ (− π 2 , π ) , v ∈ (0, 2π) .<br />
2
4.9. KONTROLNÍ OTÁZKY 49<br />
4.4 Pro plochu z předcházejícího cvičení určete tečnou rovinu a normálu v bodě, který<br />
odpovídá parametrům u = 0, v = π.<br />
4.5 Dokažte, že normála rotační plochy nemůže být mimoběžná s osou této plochy.<br />
(Návod: plochu umístěte tak, že její osa je souřadnicovou osou; dokažte, že vektor<br />
osy, vektor normály ve zvoleném bodě a polohový vektor zvoleného bodu jsou<br />
lineárně závislé.)<br />
4.6 Určete Gaussovu křivost v bodech rovníkové kružnice anuloidu. Jaké bude mít<br />
znaménko?<br />
4.9 Kontrolní otázky<br />
4.1 Uved’te, jakým postupem se konstruuje průnik dvou rotačních ploch v závislosti na<br />
poloze jejich os.<br />
4.2 Popište dva způsoby vytvoření rotačního jednodílného hyperboloidu.<br />
4.3 Vyjmenujte rotační kvadriky a rozdělte je na singulární a regulární.<br />
4.4 Uved’te nutnou a postačující podmínku <strong>pro</strong> rozpad průniku dvou rotačních kvadrik<br />
na dvě kuželosečky.
Kapitola 5<br />
Šroubové plochy<br />
5.1 Základní pojmy<br />
Obrázek 5.1:<br />
Šroubová plocha vzniká šroubovým pohybem<br />
křivky k. Šroubový pohyb je dán osou o,<br />
redukovanou výškou závitu v 0 a orientací<br />
{±} (o, v 0 , {±}). Křivku k nazýváme tvořící<br />
křivkou. Tečná rovina τ je obvykle určena<br />
tečnou ke šroubovici t s a tečnou k tvořící křivce<br />
t k .<br />
Normála šroubové plochy je kolmice k tečné<br />
rovině v bodě dotyku.<br />
Osový řez (podélný <strong>pro</strong>fil) je řez šroubové<br />
plochy rovinou σ, <strong>pro</strong>cházející osou šroubové<br />
plochy.<br />
Meridián je osový řez na jednom závitu plochy.<br />
Polomeridián je osový řez polorovinou s<br />
hraniční přímkou o na jednom závitu plochy.<br />
Čelní řez (příčný <strong>pro</strong>fil, normální řez) je řez<br />
šroubové plochy rovinou ϱ, kolmou na osu.<br />
5.2 Parametrické vyjádření šroubové plochy<br />
Šroubová plocha vznikne šroubovým pohybem tzv. tvořící křivky k kolem osy o. Necht’ osou<br />
šroubového pohybu o je souřadnicová osa z, parametr šroubového pohybu je v 0 a křivka<br />
k je rovinná (leží v rovině xz) a je dána vektorovou funkcí Y (v), v ∈ I v .<br />
Pro křivku k označme složky její vektorové rovnice<br />
Y (v) = (x(v), 0, z(v)), v ∈ I v . (5.1)<br />
50
5.3. VLASTNOSTI ŠROUBOVÝCH PLOCH 51<br />
Trajektorií bodu Y (v) křivky k je šroubovice s osou z. Pro polohový vektor bodu X<br />
šroubové plochy platí<br />
X(u, v) = (x(v) cos u, x(v) sin u, z(v) ± v 0 u) , (5.2)<br />
kde <strong>pro</strong> parametry u, v platí u ∈ R a v ∈ I v . Tak jsme odvodili vektorovou rovnici<br />
šroubové plochy <strong>pro</strong> speciální případ, kdy tvořící křivka je částí meridiánu. Konkrétní<br />
znaménko plus nebo minus v rovnici (5.2) volíme podle toho, zda jde o pravotočivý (plus)<br />
nebo levotočivý (mínus) pohyb.<br />
V obecném případě, kdy tvořící křivka je <strong>pro</strong>storová, resp. neleží v rovině xz, má<br />
šroubová plocha vyjádření<br />
X(u, v) = (x(v) cos u−y(v) sin u, x(v) sin u+y(v) cos u, z(v)±v 0 u) , u ∈ R , v ∈ I v . (5.3)<br />
Odvození uvedeného vyjádření vychází z obecného postupu vytváření ploch pomocí<br />
transformačních matic – viz str. 38.<br />
Příklad 19. Určíme parametrické vyjádření šroubové plochy, která vznikne šroubovým<br />
pohybem kružnice ležící v rovině xz se středem v bodě S = [2, 0, 0, ] a poloměrem r = 1.<br />
Osou šroubového pohybu je osa z, parametr v 0 = 3, pohyb je pravotočivý. Dále určíme<br />
tečnou rovinu a normálu plochy v bodě A = [1; 0; 0].<br />
Řešení: Tvořící křivka (kružnice) má vektorovou rovnici Y (v) = (2 + cos v, 0, sin v).<br />
Plochou je osová cyklická šroubová plocha a její vektorová rovnice je<br />
X(u, v) = ((2 + cos v) cos u, (2 + cos v) sin u, sin v + 3u), u ∈ R, v ∈ 〈0, 2π).<br />
P 1 (u, v) = ∂P = (−(2 + cos v) sin u, (2 + cos v) cos u, 3)<br />
∂u<br />
P 2 (u, v) = ∂P = (− sin v cos u, − sin v sin u, cos v).<br />
∂v<br />
Bod A = [1; 0; 0] získáme volbou parametrů u = 0, v = π, dosadíme tyto hodnoty<br />
do vypočtených parciálních derivací a dostaneme dva vektory ze zaměření tečné roviny<br />
P 1 (0, π) = (0, 1, 3), P 2 (0, π) = (0, 0, −1). Normálový vektor roviny vypočteme pomocí<br />
vektorového součinu<br />
n = P 1 (0, 0) × P 2 (0, 0) = (0, 1, 3) × (0, 0, −1) = (−1, 0, 0).<br />
Rovnice tečné roviny po dopočítání absolutního členu je x − 1 = 0 a vektorová rovnice<br />
normály n(t) = (1 − t, 0, 0), t ∈ R.<br />
□<br />
5.3 Vlastnosti šroubových ploch<br />
• Každým bodem šroubové plochy <strong>pro</strong>chází šroubovice s A , která leží na této šroubové<br />
ploše (obr. 5.1).<br />
• Každým bodem šroubové plochy <strong>pro</strong>chází (alespoň) jedna poloha tvořící křivky.
5.4. KLASIFIKACE ŠROUBOVÝCH PLOCH 52<br />
• Všechny polomeridiány jedné šroubové plochy jsou shodné.<br />
• Všechny čelní řezy jedné šroubové plochy jsou shodné.<br />
• Existuje pouze jediná rozvinutelná šroubová plocha – plocha tečen šroubovice.<br />
5.4 Klasifikace šroubových ploch<br />
Klasifikace podle tvořící křivky:<br />
Název Tvořící křivka Šroubová plocha<br />
Přímková plocha Přímka p Otevřená - p, o mimoběžky<br />
-pravoúhlá<br />
Přímka p<br />
-kosoúhlá – speciálně rozvinutelná šroubová plocha<br />
Uzavřená - p, o různoběžky<br />
-pravoúhlá<br />
-kosoúhlá – vývrtková plocha)<br />
Cyklická plocha Kružnice k - vinutý sloupek (k ∈ β, β je kolmá na o)<br />
- osová (k ∈ β, o ∈ β)<br />
- Archimédova serpentina<br />
(k ∈ β, β je kolmá k tečně t)<br />
- ostatní<br />
5.5 Úlohy na šroubových plochách<br />
Příklad 20. Sestrojíme 2 body řezu cyklické šroubové plochy polorovinou α, <strong>pro</strong>cházející<br />
osou o. - obr. 5.2.<br />
Řešení: (obr. 5.3)<br />
1. Na tvořící křivce zvolíme bod A.<br />
2. Bodem A <strong>pro</strong>ložíme šroubovici, která leží na šroubové ploše (zakreslíme půdorys).<br />
3. Sestrojíme průsečík A této šroubovice s rovinou α.<br />
4. Totéž opakujeme <strong>pro</strong> bod B.<br />
Uvědomte si , že graf závislosti je nutné konstruovat <strong>pro</strong> každý bod znovu, nebot’ <strong>pro</strong><br />
šroubovice se mění poloměr příslušné válcové plochy.<br />
Tečkovaně je vyznačen tvar celého řezu.<br />
□<br />
Příklad 21. Sestrojíme bod řezu osové cyklické šroubové plochy rovinou α (α ⊥ o). -<br />
obr. 5.4.<br />
Řešení: (obr. 5.5) Postup je podobný jako v předchozím příkladě, pouze z výšky odvozujeme<br />
délku oblouku.<br />
1. Na tvořící křivce zvolíme bod A.
5.5. ÚLOHY NA ŠROUBOVÝCH PLOCHÁCH 53<br />
Obrázek 5.2: Obrázek 5.3:<br />
2. Bodem A <strong>pro</strong>ložíme šroubovici s A , která leží na šroubové ploše (zobrazíme v půdorysu).<br />
3. Sestrojíme průsečík A této šroubovice s rovinou α. (Sestrojíme graf závislosti výšky<br />
na oblouku (rozvinutá šroubovice s A - známe v 0 a r A ). V nárysu zjistíme vzdálenost<br />
v A bodu A od roviny α. Z grafu odvodíme délku x A oblouku příslušnou k výšce v A .<br />
Délku oblouku x A naneseme na půdorys šroubovice ve směru stoupání (<strong>pro</strong>tože bod<br />
s A je pod rovinou α). Nárys bodu A najdeme v rovině α.)<br />
Další body bychom sestrojovali stejným způsobem. Uvědomte si , že graf závislosti je<br />
nutné konstruovat <strong>pro</strong> každý bod znovu (mění se poloměr).<br />
Tečkovaně je vyznačen tvar celého řezu.<br />
□<br />
Příklad 22. Sestrojíme tečnou rovinu a normálu šroubové plochy, která je určena tvořící<br />
křivkou k a šroubovým pohybem (o, v 0 , +). - obr. 5.6.<br />
Řešení: (obr. 5.7)<br />
1. Sestrojíme v bodě A tečnu r ke křivce k (nárys i půdorys).<br />
2. Sestrojíme půdorys šroubovice s <strong>pro</strong>cházející bodem A.<br />
3. Sestrojíme v bodě M tečnu t ke šroubovici s (její nárys odvodíme pomocí površky<br />
p řídícího kužele).<br />
4. Tečná rovina τ je určena tečnami t a r.<br />
5. Normála n je kolmá k tečné rovině τ (sestrojíme hlavní přímky - v našem případě<br />
je frontální hlavní přímka totožná s přímkou r).<br />
□
5.6. CVIČENÍ 54<br />
5.6 Cvičení<br />
Obrázek 5.4: Obrázek 5.5:<br />
5.1 Pomocí transformací sestavte parametrické vyjádření šroubové plochy, která vzniká<br />
pravotočivým šroubovým pohybem přímky dané body A a B okolo osy x, v 0 = 1,<br />
A[0, 1, 1], B[1, 1, 0].<br />
5.2 Sestavte parametrické vyjádření osové cyklické šroubové plochy.<br />
5.3 Sestavte parametrické rovnice uzavřené pravoúhlé přímkové šroubové plochy.<br />
5.4 Na površce plochy z předcházejícího příkladu zvolte dva různé body a výpočtem<br />
ukažte, že normály v nich nejsou kolineární.<br />
5.7 Kontrolní otázky<br />
5.1 Popište vznik tzv. Archimédovy serpentiny.<br />
5.2 Popište konstrukci normály šroubové plochy a porovnejte možnosti její konstrukce<br />
se stejnou úlohou <strong>pro</strong> rotační plochy.
5.7. KONTROLNÍ OTÁZKY 55<br />
Obrázek 5.6: Obrázek 5.7:
Kapitola 6<br />
Obalové plochy<br />
6.1 Základní pojmy<br />
Obalová plocha Ω vzniká pohybem P jiné<br />
plochy α. Plochu α nazýváme tvořící plocha.<br />
Charakteristika c je křivkou dotyku mezi<br />
tvořící plochou α a vznikající obalovou plochou<br />
Ω – obr. 6.1. Charakteristika c při pohybu<br />
P vytváří plochu Ω, tj.<br />
Obrázek 6.1:<br />
P(Ω) = P(c).<br />
Pokud chceme najít průnik obalové plochy s rovinou,<br />
najdeme charakteristiku, to znamená tvořící<br />
křivku rotační, šroubové nebo jiné plochy a tím<br />
převedeme danou úlohu na úlohu, kterou již<br />
známe z předchozích kapitol.<br />
Hlavní náplní této kapitoly je tedy hledání charakteristiky na různých typech obalových<br />
ploch.<br />
Příklady obalových ploch:<br />
Pohyb Tvořící plocha Obalová plocha<br />
Posunutí Kulová plocha Rotační válcová plocha<br />
Rotace okolo osy o Rovina ϱ ‖ o Rotační válcová plocha<br />
Rotace okolo osy o Rovina ϱ ̸‖ o Rotační kuželová plocha<br />
Rotace okolo osy o Kulová plocha, S /∈ o Anuloid<br />
Šr. pohyb s osou o Rovina ϱ ̸‖ o Rozv. šroubová plocha<br />
Šr. pohyb s osou o Kulová plocha, S /∈ o Archimédova serpentina<br />
56
6.2. CHARAKTERISTIKA ROVINY 57<br />
6.2 Charakteristika roviny<br />
Charakteristikou c roviny α při rotačním (osa o), resp. šroubovém pohybu ( o, v 0 , +), je<br />
přímka c této roviny. Platí c = α ∩ β, kde rovina β <strong>pro</strong>chází osou o a je kolmá k rovině β.<br />
• Při rotačním pohybu roviny α různoběžné s osou rotace o je výslednou obalovou<br />
plochou rotační kuželová plocha a charakteristikou (obr. 6.2) je spádová přímka,<br />
která <strong>pro</strong>tíná osu rotace .<br />
Obrázek 6.2:<br />
• Při rotačním pohybu roviny α rovnoběžné s osou o rotace je výslednou obalovou<br />
plochou rotační válcová plocha a charakteristikou je přímka rovnoběžná s osou,<br />
která má nejmenší vzdálenost od osy rotace (obr. 6.3).<br />
Obrázek 6.3:<br />
• Při šroubovém pohybu roviny α rovnoběžné s osou o je výslednou obalovou plochou<br />
opět rotační válcová plocha a charakteristikou spádová přímka, která má<br />
nejmenší vzdálenost od osy rotace.
6.2. CHARAKTERISTIKA ROVINY 58<br />
• Při šroubovém pohybu (o, v 0 , +) roviny α různoběžné s osou o je výslednou obalovou<br />
plochou plocha tečen šroubovice – rozvinutelná šroubová plocha a charakteristikou<br />
je přímka c, která je zároveň tečnou šroubovice dané šroubovým pohybem<br />
(o, v 0 , +) (obr. 6.4).<br />
Obrázek 6.4:<br />
Určení charakteristiky c je poněkud náročnější, <strong>pro</strong>to si popíšeme hledání charakteristiky<br />
roviny při šroubovém pohybu ještě v následujícím příkladě, kde přímo určíme<br />
površku k řídící kuželové plochy.<br />
Příklad 23. Sestrojíme charakteristiku roviny ρ při šroubovém pohybu (o, v 0 , +) - obr.<br />
6.5.<br />
Řešení: (obr.6.6)<br />
1. Sestrojíme libovolnou spádovou přímku s první osnovy (s 1 ⊥p ρ 1, s 2 odvodíme pomocí<br />
stopníků).<br />
2. Sestrojíme površku k řídícího kužele (V ∈ k, k ‖ s).<br />
3. Najdeme půdorysný stopník P přímky k.<br />
4. Stopníkem <strong>pro</strong>chází půdorys šroubovice (kružnice se středem v o 1 a poloměrem<br />
o 1 P 1 ).<br />
5. Sestrojíme tečnu c šroubovice. Tečna je rovnoběžná s površkou řídícího kužele k,<br />
dotykový bod najdeme na půdorysu šroubovice o 90 ◦ otočený od bodu P 1 ve směru<br />
stoupání šroubovice.<br />
6. Nárys přímky c odvodíme například pomocí stopníků nebo rovnoběžnosti c a k.<br />
7. Přímka c je hledanou charakteristikou.<br />
□
6.3. CHARAKTERISTIKA KULOVÉ PLOCHY 59<br />
Obrázek 6.5: Obrázek 6.6:<br />
6.3 Charakteristika kulové plochy<br />
Charakteristikou kulové plochy při libovolném pohybu je kružnice ležící v rovině kolmé<br />
na tečnu dráhy<br />
středu kulové plochy a <strong>pro</strong>cházející středem kulové plochy. Kružnice má stejný poloměr<br />
jako kulová plocha.<br />
• Při posunutí kulové plochy ve směru přímky o je výslednou obalovou plochou rotační<br />
válcová plocha a charakteristikou kružnice, která leží v rovině kolmé na směr pohybu<br />
a <strong>pro</strong>cházející středem kulové plochy (obr. 6.7).<br />
Obrázek 6.7:<br />
• Charakteristikou c kulové plochy při rotačním pohybu (osa o) je kružnice ležící v<br />
rovině kolmé na tečnu ke kružnici, kterou opisuje střed kulové plochy při rotačním
6.3. CHARAKTERISTIKA KULOVÉ PLOCHY 60<br />
pohybu (rovina <strong>pro</strong>chází středem kulové plochy). Z toho plyne, že charakteristika<br />
c kulové plochy při rotaci leží v rovině určené osou o rotace a středem S kulové<br />
plochy. Vzniklou obalovou plochou je anuloid (obr. 6.8).<br />
Obrázek 6.8:<br />
• Charakteristikou c kulové plochy při šroubovém pohybu (o, v 0 , ±), je kružnice<br />
ležící v rovině kolmé na tečnu šroubovice, po které se pohybuje střed kulové plochy.<br />
Vzniklou obalovou plochou je Archimédova serpentina (obr. 6.9).<br />
Obrázek 6.9:<br />
V dalších odstavcích jsou popsány metody, které umožňují konstrukci jednotlivých bodů<br />
charakteristiky v případě, že tvořící plochou je plocha rotační (metoda kulových ploch),
6.4. METODA KULOVÝCH PLOCH 61<br />
6.4 Metoda kulových ploch<br />
Užití: tvořící plocha je rotační.<br />
1. Na tvořící ploše α zvolíme rovnoběžkovou kružnici p.<br />
2. Určíme kulovou plochu τ, která se dotýká tvořící plochy α podél kružnice p.<br />
3. Určíme charakteristiku c kulové plochy τ při daném pohybu 1 .<br />
4. Společné body (pokud existují) charakteristiky c a rovnoběžkové kružnice p náleží<br />
hledané charakteristice plochy α při daném pohybu 2 .<br />
Obrázek 6.10: Obrázek 6.11:<br />
Příklad 24. Sestrojíme dva body charakteristiky komolého rotačního kužele při rotaci<br />
okolo osy o - obr. 6.10.<br />
Řešení: (obr.6.11)<br />
Řešení vychází z poznámek uvedených v obecném postupu, tj. konstruována je jen<br />
rovina charakteristiky.<br />
1. Na tvořící ploše α (kuželi) zvolíme rovnoběžkovou kružnici p.<br />
2. Určíme kulovou plochu τ, která se dotýká tvořící plochy α podél kružnice p.<br />
3. Určíme charakteristiku c kulové plochy τ při daném pohybu. Charakteristikou kulové<br />
plochy je kružnice, která se do půdorysu <strong>pro</strong>mítne jako úsečka AB, nárys nemusíme<br />
konstruovat.<br />
1 Stačí určit jen rovinu γ, v níž leží charakteristika c.<br />
2 Pokud jsme v předcházejícím bodě našli jen rovinu γ, určíme případné průsečíky roviny γ s<br />
rovnoběžkovou kružnicí p.
6.4. METODA KULOVÝCH PLOCH 62<br />
4. Body charakteristiky (pokud existují) jsou průsečíky kružnice p a charakteristiky<br />
kulové plochy τ (v půdorysu sestrojíme průsečíky X, Y a odvodíme na kružnici p<br />
do nárysu).<br />
5. Další body charakteristiky bychom sestrojili podobně, jen zvolíme novou rovnoběžkovou<br />
kružnici a vepsanou kulovou plochu. Celý postup zopakujeme.<br />
Příklad 25. Sestrojíme hlavní meridián obalové plochy vzniklé rotací rotačního kužele<br />
při rotaci okolo osy o - obr. 6.12.<br />
Řešení: (obr.6.13)<br />
1. Použijeme postup z příkladu 24 a sestrojíme body X, Y charakteristiky.<br />
2. Dále postupujeme stejně jako při sestrojování meridiánu rotační plochy (body X, Y<br />
jsou body tvořící křivky: Sestrojíme rovnoběžkovou kružnici rotační plochy s osou<br />
o <strong>pro</strong>cházející body X, Y . Průsečíky X ′ a Y ′ rovnoběžkových kružnic s rovinou<br />
meridiánu µ jsou body meridiánu).<br />
3. Další body a získáme novou volbou rovnoběžkové kružnice p a vepsané kulové plochy<br />
a celý postup zopakujeme.<br />
□<br />
Na obrázku je vyznačen tvar charakteristiky a meridiánu.<br />
□<br />
o 2<br />
o 1<br />
m 1<br />
V 2<br />
V 1<br />
Obrázek 6.12:<br />
Y 2<br />
p 2 V 2<br />
p X 1=Y1<br />
1<br />
V 1<br />
X 2<br />
Y' 2<br />
o 1<br />
o 2<br />
X' 2<br />
X' =Y' 1 1<br />
Obrázek 6.13:<br />
Příklad 26. Sestrojíme dva body charakteristiky obalové plochy vzniklé šroubovým pohybem<br />
(o, v 0 , +) rotačního kužele - obr. 6.14.<br />
Řešení: (obr.6.15)
6.5. METODA TEČNÝCH ROVIN 63<br />
1. Na tvořící ploše α (kuželi) zvolíme rovnoběžkovou kružnici p.<br />
2. Určíme kulovou plochu τ, která se dotýká tvořící plochy α podél kružnice p.<br />
3. Určíme charakteristiku c kulové plochy τ při daném pohybu. Charakteristikou kulové<br />
plochy je kružnice. Ta leží v rovině kolmé k tečně šroubovice, po které se pohybuje<br />
střed kulové plochy τ. (Sestrojíme tečnu t a hlavní přímky roviny <strong>pro</strong>cházející<br />
středem kulové plochy a kolmé na tečnu.)<br />
4. Body charakteristiky (pokud existují) jsou průsečíky kružnice p a charakteristiky<br />
kulové plochy τ. V půdorysu sestrojíme průsečíky X, Y a odvodíme do nárysu. (Dvě<br />
kružnice na kulové ploše mohou mít nejvýše dva průsečíky. Proto je zřejmé, že dva<br />
průsečíky v nárysu jsou jen zdánlivé. Nárys a půdorys skutečného průsečíku musí<br />
ležet na ordinále.)<br />
5. Další body charakteristiky bychom sestrojili podobně, jen zvolíme novou rovnoběžkovou<br />
kružnici a vepsanou kulovou plochu. Celý postup zopakujeme.<br />
□<br />
V 2<br />
v 0<br />
o 1<br />
o 2<br />
f 2<br />
t 2<br />
t 2<br />
V 2<br />
X 2<br />
h 2<br />
p 2<br />
Y 2<br />
v 0<br />
P 2<br />
P 1<br />
X 1<br />
V 1<br />
f 1<br />
h 1<br />
t 1<br />
p 1<br />
Y 1<br />
o 1<br />
o 2<br />
t 1<br />
V 1<br />
Obrázek 6.14:<br />
Obrázek 6.15:<br />
6.5 Metoda tečných rovin<br />
Užití: Tvořící plocha α je rozvinutelná.<br />
1. Na tvořící ploše α zvolíme povrchovou přímku p.<br />
2. Určíme rovinu τ, která se dotýká tvořící plochy α podél přímky p.<br />
3. Určíme charakteristiku c roviny τ při daném pohybu.<br />
4. Společné body (pokud existují) charakteristiky c a površky p náleží hledané charakteristice<br />
plochy α při daném pohybu.
6.5. METODA TEČNÝCH ROVIN 64<br />
Příklad 27. Sestrojíme charakteristiku a hlavní meridián obalové plochy vzniklé rotací<br />
šikmého kruhového válce při rotaci okolo osy o - obr. 6.16.<br />
Řešení: (obr.6.17)<br />
Řešení vychází z obecného postupu.<br />
1. Na tvořící ploše α (šikmém kruhovém válci) zvolíme povrchovou přímku p.<br />
2. Určíme rovinu τ, která se dotýká tvořící plochy α podél přímky p: V průsečíku<br />
přímky p s podstavou válce sestrojíme tečnu t k podstavě. Tečna t leží v půdorysně,<br />
<strong>pro</strong>to její nárys splyne s osou x 12 . Přímky p a t určují tečnou rovinu τ.<br />
3. Určíme charakteristiku c roviny τ při rotačním pohybu. Je to spádová přímka roviny<br />
τ (v půdorysu kolmá na t, <strong>pro</strong>tože t je hlavní přímkou roviny τ).<br />
4. Průsečík charakteristiky c a površky p je jedním bodem hledané charakteristice<br />
plochy α při daném pohybu. Označíme ho X.<br />
5. Dále postupujeme stejně jako při sestrojování meridiánu rotační plochy (X je bod<br />
tvořící křivky: Sestrojíme rovnoběžkovou kružnici rotační plochy s osou o <strong>pro</strong>cházející<br />
bodem X. Průsečík X ′ rovnoběžkové kružnice s rovinou meridiánu µ je bod meridiánu).<br />
6. Další body získáme novou volbou površky p a opakováním celého postupu.<br />
Na obrázku je vyznačen tvar charakteristiky a meridiánu.<br />
□<br />
X 2<br />
X' 2<br />
t=x 2 12<br />
o 2<br />
p 2<br />
c 1<br />
o 1 X' 1<br />
m 1<br />
X p 1 1<br />
t 1<br />
Obrázek 6.16:<br />
Obrázek 6.17:<br />
Příklad 28. Sestrojíme charakteristiku obalové plochy vzniklé šroubovým pohybem (o,<br />
v 0 , +) kruhového kužele - obr. 6.18.<br />
Řešení: (obr.6.19)<br />
Tuto úlohu není možné řešit metodou kulových ploch (tvořící plocha není rotační, jde<br />
o kruhový, tj. šikmý kužel).<br />
Řešení vychází z obecného postupu.
6.6. URČENÍ OBALOVÉ PLOCHY VÝPOČTEM 65<br />
Obrázek 6.18: Obrázek 6.19:<br />
1. Na tvořící ploše α (kuželi) zvolíme povrchovou přímku p.<br />
2. Určíme rovinu τ, která se dotýká tvořící plochy α podél přímky p: V průsečíku<br />
přímky p s podstavou válce sestrojíme tečnu t k podstavě. Přímky p a t určují<br />
tečnou rovinu τ. Tečna t je hlavní přímkou roviny τ (je rovnoběžná s půdorysnou),<br />
určíme ještě ještě jednu hlavní přímku <strong>pro</strong>cházející vrcholem V , popř. stopy roviny<br />
τ (zde jsme našli pouze nárysnou stopu).<br />
3. Určíme charakteristiku c roviny τ při šroubovém pohybu pomocí postupu z příkladu<br />
23.<br />
4. Průsečík charakteristiky c a površky p je jedním bodem hledané charakteristice<br />
plochy α při daném pohybu. Označíme ho X.<br />
5. Další body bychom získali novou volbou površky p a opakováním celého postupu.<br />
□<br />
Úlohu 24 by bylo možné řešit nejen metodou kulových ploch, ale i metodou tečných<br />
rovin.<br />
6.6 Určení obalové plochy výpočtem<br />
Uvažujme nyní obecnější případ, totiž situaci, kdy tvořící plocha koná nejen pohyb, ale<br />
navíc se může v závislosti na parametru pohybu tato tvořící plocha měnit. Předpokládáme,<br />
že tvořící plocha a vznikající obalová plocha se <strong>pro</strong> každou hodnotu parametru dotýkají<br />
podél křivky a nemají společné části (plochy). Podobně jako v případě křivek můžeme<br />
formulovat větu, která je teoretickým východiskem <strong>pro</strong> stanovení rovnice obalové plochy.
6.6. URČENÍ OBALOVÉ PLOCHY VÝPOČTEM 66<br />
Věta 11. Pro obalovou plochu jednoparametrického systému ploch f(x, y, z, α) = 0 platí:<br />
<strong>pro</strong> bod [x, y, z] ležící na obalové ploše existuje α tak, že<br />
f(x, y, z, α) = 0<br />
a<br />
∂<br />
f(x, y, z, α) = 0 .<br />
∂α<br />
Tedy popis obalové plochy získáme tak, že ze soustavy (obecně nelineárních algebraických<br />
rovnic)<br />
∂<br />
f(x, y, z, α) = 0 , f(x, y, z, α) = 0<br />
∂α<br />
eliminujeme (vyloučíme) α.<br />
Příklad 29. Uvažujme systém jednotkových kulových ploch:<br />
Určete obalovou plochu a charakteristiku.<br />
(x − α) 2 + y 2 + z 2 − 1 = 0 .<br />
Řešení: Podle věty 11 stanovíme příslušnou parciální derivaci a <strong>pro</strong>vedeme vyloučení<br />
pohybového parametru:<br />
∂f<br />
∂α<br />
= 2(x − α) · (−1) = 0 ⇒ x − α = 0.<br />
Rovnice obalové plochy je y 2 + z 2 − 1 = 0, což je v E 3 rotační válcová plocha a v E 2<br />
charakteristika (v rovině x = α). Výsledek je očekávaný, nebot’ zadán byl posuvný pohyb<br />
jednotkové kulové plochy ve směru osy x.<br />
□<br />
Příklad 30. Uvažujme systém kulových ploch:<br />
Určete obalovou plochu.<br />
(x − 2α) 2 + y 2 + z 2 − α 2 = 0 .<br />
Řešení: Opět jde o posouvání kulové plochy, ale kulová plocha nyní mění při tomto<br />
pohybu poloměr, a to poloviční rychlostí, než je rychlost pohybu. Postupujeme opět podle<br />
věty 11 :<br />
∂f<br />
∂α = 2(x − 2α) · (−2) − 2α = 0 ⇒ α = 3 2 x .<br />
Rovnice obalové plochy je − 1 3 x2 +y 2 +z 2 = 0, což je v rotační kuželová plocha s vrcholem<br />
v počátku a s osou v ose x.<br />
□
6.7. CVIČENÍ 67<br />
6.7 Cvičení<br />
6.1 Uvažujte jednoparametrický systém rovin cos α·x−sin α·y−z = 0 a určete příslušnou<br />
obalovou plochu.(Návod: <strong>pro</strong> vyloučení parametru použijte umocnění každé z rovnic<br />
na druhou a sečtěte je.)<br />
6.2 Pro rovinu rovnoběžnou s osou určete obalovou plochu, která vzniká rotací této<br />
roviny okolo osy. (Návod: Za osu rotace zvolte některou souřadnicovou osu, sestavte<br />
implicitní rovnici rovnoběžné roviny ve vhodné poloze a pak do rovnice roviny<br />
zaved’te parametr rotace okolo zvolené souřadnicové osy. Další výpočet již <strong>pro</strong>ved’te<br />
aplikováním věty 11.)<br />
6.8 Kontrolní otázky<br />
6.1 Definujte charakteristiku obalové plochy a vysvětlete význam této křivky <strong>pro</strong> řešení<br />
dalších úloh o obalových plochách.<br />
6.2 Pro které tvořící plochy lze <strong>pro</strong> konstrukci charakteristiky použít metodu kulových<br />
ploch a <strong>pro</strong> které metodu tečných rovin.<br />
6.3 Uved’te příklad tvořicí plochy, jejíž charakteristiku lze konstruovat jak metodou<br />
tečných rovin, tak metodou kulových ploch. Uměli byste pojmenovat všechny takové<br />
plochy?<br />
6.4 Jak se liší úlohy, které lze řešit pomocí uvedených metod graficky a výpočetně?<br />
Uved’te příklad úlohy, kterou můžete řešit jen výpočetně.
Kapitola 7<br />
Rozvinutelné plochy<br />
7.1 Základní pojmy<br />
Torzální površkou přímkové plochy rozumíme přímku p, <strong>pro</strong> kterou platí, že v každém<br />
jejím bodě je stejná tečná rovina τ, tj. tečná rovina τ se dotýká plochy podél torzální<br />
površky p.<br />
Přímková plocha je rozvinutelná, jestliže všechny její površky jsou torzální.<br />
Rozvinutelná plocha je obalovou plochou pohybující se roviny.<br />
Věta 12. Plocha je rozvinutelná, právě když ve všech jejích bodech je Gaussova křivost<br />
nulová.<br />
7.2 Typy rozvinutelných ploch<br />
Věta 13. Rozvinutelnými plochami jsou pouze následující plochy a jejich části: rovina,<br />
válcové plochy – obr. 7.1, kuželové plochy – obr. 7.2 a plochy tečen <strong>pro</strong>storových<br />
křivek – obr. 7.3.<br />
Obrázek 7.1: Obrázek 7.2:<br />
68
7.3. METODY KOMPLANACE 69<br />
Válcová plocha je určena rovinnou křivku k (k ⊂ σ) a směrem s, který nenáleží<br />
dané rovině (s ̸‖ σ), a je tvořena přímkami, které <strong>pro</strong>tínají křivku k a jsou směru s.<br />
Kuželová plocha je určena rovinnou křivku k (k ⊂ σ) a bodem V , který neleží v<br />
rovině dané křivky (V ∉ σ), a je tvořena přímkami, které <strong>pro</strong>tínají křivku k a <strong>pro</strong>cházejí<br />
bodem V .<br />
V <strong>pro</strong>jektivním rozšíření euklidovského <strong>pro</strong>storu lze definovat válcovou a kuželovou<br />
plochu jednou definicí, a to jako množinu přímek, které <strong>pro</strong>tínají danou křivku k a<br />
<strong>pro</strong>cházejí daným vrcholem V . Oba typy ploch se liší tím, zda vrchol V je vlastní, pak<br />
jde o kuželovou plochu, nebo je nevlastní, pak jde o válcovou plochu.<br />
Obrázek 7.3: Obrázek 7.4:<br />
Plocha tečen <strong>pro</strong>storové křivky je určena <strong>pro</strong>storovou křivkou k a je tvořena jejími<br />
tečnami. Na obr. 7.3 jsou uvedeny dva příklady takové plochy. Příkladem plochy tečen je<br />
rozvinutelná šroubová plocha, která je tvořena tečnami šroubovice – obr. 7.4. Řezem této<br />
plochy rovinou kolmou k ose šroubového pohybu je kruhová evolventa, tj. křivka, která<br />
vzniká jako trajektorie bodu přímky odvalující se po kružnici.<br />
7.3 Metody komplanace<br />
Komplanací neboli rozvinutím rozumíme zobrazení ϕ rozvinutelné plochy do roviny,<br />
které zachovává délky a úhly.<br />
Obecné metody <strong>pro</strong> rozvinutí jsou dány následující tabulkou.<br />
Typ rozvinutelné plochy<br />
Obecná válcová plocha<br />
Obecná kuželová plocha<br />
Plocha tečen <strong>pro</strong>storové křivky<br />
Metoda rozvinutí<br />
Normálový řez<br />
Triangulace<br />
Triangulace<br />
7.3.1 Metoda normálového řezu<br />
Normálovým řezem válcové plochy rozumíme řez rovinou kolmou na povrchové<br />
přímky plochy. Takový řez se při rozvinutí zobrazí na přímku kolmou na obrazy površek.<br />
Při rozvinutí válcové plochy postupujeme takto:
7.3. METODY KOMPLANACE 70<br />
1. Vedeme libovolnou rovinu ϱ kolmou na povrchové přímky válcové plochy.<br />
2. Určíme řez k dané válcové plochy rovinou ϱ.<br />
3. V rozvinutí se křivka k zobrazí do úsečky 0 k. Délka obrazu se rovná délce vzoru, tj.<br />
délku úsečky 0 k určíme pomocí rektifikace křivky k.<br />
Pokud chceme v rozvinutí zobrazit další křivku ležící na dané obecné válcové ploše,<br />
stačí na povrchové přímky vynášet úseky površky mezi normálovým řezem a danou<br />
křivkou.<br />
Normálovým řezem na rotační válcové ploše je např. její podstava. Oblouk šroubovice<br />
ležící na dané rotační válcové ploše se rozvine do úsečky.<br />
Obrázek 7.5: Obrázek 7.6:<br />
Příklad 31. Na obr. 7.5 je <strong>pro</strong>vedeno rozvinutí poloviny pláště rotačního válce s řezem<br />
rovinou σ. Normálovým řezem je podstava k. Vzdálenost x površek v rozvinutí se rovná<br />
délce oblouku na podstavě.<br />
Příklad 32. Na obr. 7.6 je <strong>pro</strong>vedeno rozvinutí poloviny pláště kruhového (kosého) válce.<br />
Rovina ϱ normálového řezu je zobrazena v nárysu (volíme jednu z rovin kolmých na<br />
površky). Normálovým řezem je elipsa, jejíž hlavní poloosa se rovná poloměru kružnice<br />
podstavy. Normálový řez je vyznačen ve sklopení. Délky oblouků elipsy ve sklopení určují<br />
vzdálenosti jednotlivých površek v rozvinutí (např. délky x a y). V daném případě mají<br />
v rozvinutí všechny površky stejnou délku. Poměr, v němž dělí bod normálového řezu<br />
površku, zjistíme z nárysu, nebot’ površky jsou rovnoběžné s nárysnou.<br />
7.3.2 Metoda triangulace<br />
Podstatou této metody je náhrada plochy mnohostěnem, který má trojúhelníkové stěny.<br />
V případě kuželových ploch volíme trojúhelníky tak, že mají vždy jeden vrchol ve<br />
vrcholu kuželové plochy. Pro rotační kuželovou plochu platí, že podstava k se rozvine<br />
do oblouku kružnice, jehož délka se musí rovnat obvodu kružnice k. Poloměr oblouku v<br />
rozvinutí se rovná délce úseku površky mezi vrcholem a podstavou.
7.4.<br />
TEČNA KŘIVKY V ROZVINUTÍ 71<br />
Obrázek 7.7: Obrázek 7.8:<br />
Příklad 33. Na obr. 7.7 je zobrazeno rozvinutí části rotační kuželové plochy. Pro určení<br />
skutečných délek úseků površek plochy je využito rotace površky do roviny obrysové<br />
površky.<br />
Příklad 34. Na obr. 7.8 je zobrazeno rozvinutí části kruhové kuželové plochy. Použita<br />
je triangulace a celý postup spočívá v určování skutečných délek úseček (úseků površek<br />
plochy). K tomu je využito otočení do polohy rovnoběžné s nárysnou. Površky určené<br />
bodem 1, resp. 7, na podstavě se zobrazují v nárysu ve skutečné velikosti.<br />
7.4 Tečna křivky v rozvinutí<br />
Obrazem tečny křivky na ploše je tečna křivky v rozvinutí.<br />
Vzhledem k tomu, že rozvinutí je zobrazení, které zachovává úhly, je možné určit tečnu<br />
křivky v rozvinutí pomocí určení úhlu površky a tečny křivky na ploše.<br />
Příklad 35. Na obr. 7.7 je zkonstruována tečna křivky řezu v rozvinutí. K určení úhlu<br />
tečny a površky je využito trojúhelníka 3P 1¯3, <strong>pro</strong> nějž je určena skutečná velikost pomocí<br />
skutečných délek jeho stran. Bod ¯3 je bodem řezu, bod 3 leží na podstavě a bod P 1 je<br />
průsečíkem tečny s podstavnou rovinou. Přímka 3P 1 je tečnou podstavy.<br />
7.5 Rozvinutí rozvinutelné šroubové plochy<br />
Rozvinutelnou šroubovou plochu lze rozvinout tak, že určíme obraz hrany vratu, tj.<br />
určující šroubovice. Platí, že šroubovice vratu se v rozvinutí zobrazí do kružnice, <strong>pro</strong><br />
jejíž poloměr ρ platí<br />
ρ = r2 + v0<br />
2 ,<br />
r<br />
což je převrácená hodnota první křivosti šroubovice v souladu s větou 7 (str. 29).
7.6. KONSTRUKCE A ROZVINUTÍ PŘECHODOVÉ ROZVINUTELNÉ PLOCHY 72<br />
Příklad 36. Na obr. 7.9 je zobrazeno rozvinutí části rozvinutelné šroubové plochy. Pro<br />
šroubovici vratu je určen poloměr ρ, který je poloměrem příslušného oblouku v rozvinutí.<br />
Obrazem kruhové evolventy, která je řezem dané plochy půdorysnou, je opět kruhová<br />
evolventa. Pro zobrazení daných površek v rozvinutí byla určena k otočení, které odpovídá<br />
oblouku ω, délka oblouku šroubovice ¯ω.<br />
Obrázek 7.9:<br />
7.6 Konstrukce a rozvinutí přechodové rozvinutelné<br />
plochy<br />
Uvažujme dvě rovinné křivky a a b ležící v rovinách α a β – obr. 7.10. V řadě technických<br />
aplikací vzniká požadavek na určení rozvinutelné plochy Ω, která obsahuje obě dané křivky<br />
(a ⊂ Ω, b ⊂ Ω). Plochu Ω nazýváme přechodová plocha mezi danými křivkami.<br />
Postup konstrukce přechodové plochy:<br />
1. Na jedné z křivek zvolíme bod – např. A ∈ a a určíme tečnu t A křivky a v bodě A.<br />
2. Na druhé křivce, tj. na křivce b, určíme bod B tak, aby tečna t B v tomto bodě<br />
nebyla v tečnou t A mimoběžná. Tento krok realizujeme takto:<br />
t A ‖ β – vedeme tečnu t B křivky b rovnoběžnou s přímkou t A – obr. 7.11,<br />
t A ̸‖ β – označme p průsečnici rovin α a β; z průsečíku t A ∩ p vedeme tečnu t B<br />
křivky b – obr. 7.10.
7.7. KONTROLNÍ OTÁZKY 73<br />
Obrázek 7.10: Obrázek 7.11:<br />
3. Přímka AB je torzální přímkou – tečná rovina v bodech A a B je stejná a tato<br />
rovina se dotýká vytvářené plochy i ve všech bodech této površky.<br />
Zkonstruovaná přechodová plocha je vždy bud’ plochou tečen <strong>pro</strong>storové křivky (zpravidla<br />
neznámé či neurčované), nebo ve výjimečných případech plochou válcovou nebo kuželovou.<br />
Rozvinutí přechodové plochy se <strong>pro</strong>vede zpravidla pomocí triangulace.<br />
7.7 Kontrolní otázky<br />
7.1 Definujte torzální površku plochy.<br />
7.2 Definujte rozvinutelné plochy a uved’te všechny typy rozvinutelných ploch.<br />
7.3 Vysvětlete pojem Gaussova křivost.<br />
7.4 Uved’te příklad plochy, která je přímková, ale není rozvinutelná.<br />
7.5 Uved’te dva způsoby vytvoření rozvinutelné šroubové plochy (návod: jako obalovou<br />
plochu a jako jeden z typů rozvinutelných ploch).<br />
7.6 Popište metodu normálového řezu <strong>pro</strong> rozvinutí. Pro které rozvinutelné plochy se<br />
tato metoda dá aplikovat?
Kapitola 8<br />
Některé nekartézské souřadnicové<br />
soustavy<br />
V řadě aplikací matematiky se používají k vhodnému analytickému popisu geometrického<br />
útvaru v E 3 souřadnice, které nejsou kartézské. Jedná se o souřadnice afinní (souřadnicové<br />
osy nemusí být na sebe kolmé), sférické (kulové), cylindrické (válcové) apod.<br />
Uvedeme vztahy, pomocí nichž lze přejít od kartézských souřadnic k souřadnicím<br />
sférickým a cylindrickým.<br />
8.1 Sférické souřadnice<br />
Sférické souřadnice jsou <strong>pro</strong>storovou analogií polárních souřadnic v rovině.<br />
Rovnice<br />
x = ρ · cos ϕ cos ψ , y = ρ · sin ϕ cos ψ , z = ρ · sin ψ , (8.1)<br />
v nichž ρ > 0, ϕ ∈ 〈0, 2π) a ψ ∈ 〈− π , dπ 〉, vyjadřují přechod k tzv. sférickým souřadnicím<br />
2 d2<br />
[ρ, ϕ, ψ].<br />
Číslo ρ = √ x 2 + y 2 + z 2 vyjadřuje vzdálenost bodu X od počátku O, ϕ a ψ jsou<br />
orientované úhly ( zeměpisná šířka a délka“) – obr. 8.1.<br />
”<br />
S rovnicemi (8.2) a (8.1) se výhodně pracuje při sledování <strong>pro</strong>blémů spojených s rotací<br />
a souměrností.<br />
8.2 Cylindrické souřadnice<br />
Rovnice<br />
x = ρ cos ϕ , y = ρ sin ϕ , z = z , (8.2)<br />
v nichž ρ > 0 a ϕ ∈ 〈0, 2π) popisují vztah tzv. cylindrických souřadnic [ρ, ϕ, z] s kartézskými<br />
souřadnicemi.<br />
Vidíme, že ρ = √ x 2 + y 2 vyjadřuje vzdálenost bodu X od osy z a ϕ je orientovaný<br />
úhel s počátečním ramenem v kladné poloose x a koncovým ramenem na polopřímce OX 1 ,<br />
kde X 1 je pravoúhlý průmět bodu X do souřadnicové roviny xy – obr. 8.2.<br />
Ve speciálním případě (8.2), kdy z = 0, hovoříme o polárních souřadnicích v rovině<br />
E 2 .<br />
74
8.3. VYUŽITÍ NEKARTÉZSKÝCH SOUŘADNIC 75<br />
Obrázek 8.1: Obrázek 8.2:<br />
8.3 Využití nekartézských souřadnic<br />
Použití uvedených nekartézských souřadnic vede ke zjednodušení analytického vyjádření<br />
útvarů (zkratka konst. označuje kladnou konstantu).<br />
1. ρ =konst. popisuje v případě sférických souřadnic kulovou plochu se středem O<br />
a poloměrem ρ,<br />
2. ρ =konst. popisuje v případě cylindrických souřadnic rotační válcovou plochu o poloměru<br />
ρ a s osou z,<br />
3. ψ =konst. určuje v případě sférických souřadnic rotační kuželovou plochu,<br />
4. ρ =konst. určuje v polárních souřadnicích kružnici se středem O a poloměrem ρ.<br />
8.4 Cvičení<br />
8.1 V kartézské soustavě souřadnic zobrazte body, jejichž polární souřadnice jsou A [ ]<br />
3, π 6 ,<br />
B [ ] [ ] [<br />
1, 2π 3 , C 2, −<br />
π<br />
4 . Jaké jsou kartézské souřadnice bodu B? [B − 1, √ ]<br />
3<br />
]<br />
2 2<br />
8.2 Vypočtěte velikost úsečky AB, znáte-li polární souřadnice bodů A [ ] [ ]<br />
3, 11π<br />
18 , B 4,<br />
π<br />
3 .<br />
[5]<br />
8.3 Bod A má kartézské souřadnice A[−1, 1, 2]. Jaké jsou jeho cylindrické souřadnice.<br />
[[ √ 2, 3 4 , 2]]<br />
8.4 Bod A má cylindrické souřadnice A[1, 1, 1]. Vypočtěte jeho kartézské souřadnice<br />
s přesností na tři desetinná místa.<br />
[[0, 540; 0, 841; 1, 000]]<br />
8.5 Jaké jsou sférické souřadnice bodu A, jsou-li jeho souřadnice v kartézské soustavě<br />
A[1, 1, 1]? [ρ = √ 3, ϕ = π 4 , ψ = arctg 1 √<br />
2<br />
]
8.5. KONTROLNÍ OTÁZKY 76<br />
8.6 Víme, že sférické souřadnice bodu A jsou ρ = 1, ϕ = − π, ψ = π . Jaké jsou jeho<br />
3 6 [<br />
kartézské souřadnice? [ − 3, √ ]<br />
3<br />
, 1 ]<br />
4 4 2<br />
8.7 V systému AutoCAD se používá následujících symbolů: @ – relativní souřadnice<br />
(tj. souřadnice vzhledem k aktuálnímu bodu, nikoliv k počátku), < – zadání úhlu.<br />
Zřejmě zadáním 20 < 45 < 30 určujeme bod pomocí sférických souřadnic. Určete<br />
typ souřadnic <strong>pro</strong> zadání<br />
a) @100 < 45, b) 40 < 60, 10.<br />
[a) relativní polární souřadnice, b) cylindrické souřadnice]<br />
8.5 Kontrolní otázky<br />
8.1 Uved’te, které body nemají jednoznačně určeny sférické souřadnice.<br />
8.2 Uved’te, které body nemají jednoznačně určeny cylindrické souřadnice.
Kapitola 9<br />
Nelineární útvary v rovině<br />
a v <strong>pro</strong>storu<br />
9.1 Vyjádření křivek<br />
Uved’me si dále vektorové rovnice některých křivek.<br />
9.1.1 Kružnice<br />
Kružnice o středu O a poloměru r (r > 0) má vektorovou rovnici<br />
X(t) = (r · cos t, r · sin t), t ∈< 0, 2π). (9.1)<br />
Parametr t je úhel, který svírá polohový vektor X(t) s kladnou poloosou x (obr. 9.1).<br />
Snadno zjistíme, že<br />
√<br />
|X(t)| = r 2 cos 2 t + r 2 sin 2 t = r ,<br />
neboli vzhledem ke vztahu (9.1) x 2 + y 2 = r 2 .<br />
Jestliže má kružnice k střed v bodě S[m, n] a je-li její poloměr r, <strong>pro</strong>vedeme posunutí<br />
kružnice o vektor s = (−m, −n). Kružnice k přejde do kružnice k ′ = (O, r), kde O je<br />
počátek systému souřadnic. Rovnice kružnice k = (S, r) má tedy tvar<br />
(x − m) 2 + (y − n) 2 = r 2 .<br />
Příklad 37. Sestavte vektorovou a parametrickou rovnici kružnice k daného poloměru r,<br />
jestliže se kružnice dotýká souřadnicových os v jejich kladné části.<br />
Řešení: Středem hledané kružnice je bod S[r, r]. Vektorovou rovnici kružnice k získáme<br />
z rovnice (9.1) přičtením polohového vektoru S bodu S k pravé straně rovnice, tj. platí<br />
X(t) = S + (r · cos t, r · sin t) = (9.2)<br />
= (r + r · cos t, r + r · sin t) , t ∈< 0, 2π) .<br />
77
9.1. VYJÁDŘENÍ KŘIVEK 78<br />
Obrázek 9.1: Obrázek 9.2:<br />
Parametrické vyjádření kružnice k je tvaru<br />
x = r + r · cos t , y = r + r · sin t , t ∈< 0, 2π) .<br />
Příklad 38. Sestavíme parametrické vyjádření epicykloidy, tj. křivky, kterou vytváří<br />
bod X při odvalování kružnice h ”<br />
vnějším obvodem“ po ”<br />
vnějším obvodu“ kružnice p.<br />
Uvažujme kružnice h = (H, r) a p = (P, r), kde H[2r, 0], P = O – obr. 9.2. Bod X[r, 0] je<br />
bodem dotyku daných kružnic.<br />
Řešení: Parametrické rovnice epicykloidy lze sestavit na základě obr. 9.3. Stačí vyjádřit<br />
souřadnice bodu H ′ a pak relativně k němu souřadnice bodu X ′′ .<br />
Jinou možnost řešení úlohy představuje využití geometrických transformací. Epicykloidální<br />
pohyb T, tj. pohyb určený odvalováním kružnice h po kružnici p, je geometrickou<br />
transformací, kterou můžeme složit následujícím způsobem<br />
T = R H ′ ,t ◦ R P,t = P H<br />
′ ◦ R P,t ◦ P −H ′ ◦ R P,t, (9.3)<br />
kde t je úhel a H ′ je polohový vektor bodu H ′ – obr. 9.3. Epicykloidální pohyb můžeme<br />
tedy složit z rotace okolo počátku P o úhel t, posunutí o vektor −H ′ , další rotace okolo<br />
počátku o úhel t a z posunutí o vektor H ′ .<br />
Uvedené geometrické transformace zapíšeme maticově. Pro matici výsledné transformace<br />
platí<br />
□<br />
T =<br />
⎛<br />
⎝<br />
⎛<br />
· ⎝<br />
cos t, sin t, 0<br />
− sin t, cos t, 0<br />
0, 0, 1<br />
⎞<br />
⎛<br />
⎠ · ⎝<br />
1, 0, 0<br />
0, 1, 0<br />
2r cos t, 2r sin t, 1<br />
⎞<br />
1, 0, 0<br />
0, 1, 0<br />
−2r cos t, −2r sin t, 1<br />
⎛<br />
⎠ = ⎝<br />
⎞<br />
⎛<br />
⎠ · ⎝<br />
cos t, sin t, 0<br />
− sin t, cos t, 0<br />
0, 0, 1<br />
cos 2t, sin 2t, 0<br />
− sin 2t, cos 2t, 0<br />
2r(cos t − cos 2t), 2r(sin t − sin 2t), 1<br />
⎞<br />
⎠ .<br />
⎞<br />
⎠ ·
9.1. VYJÁDŘENÍ KŘIVEK 79<br />
Pro bod X ′′ , který je bodem epicykloidy vytvářené bodem X, platí při využití homogenních<br />
souřadnic X ′′ = X · T, tj.<br />
⎛<br />
cos 2t, sin 2t,<br />
⎞<br />
0<br />
X ′′ = (r, 0, 1) · ⎝ − sin 2t, cos 2t, 0 ⎠ =<br />
2r(cos t − cos 2t), 2r(sin t − sin 2t), 1<br />
= (2r cos t − r cos 2t, 2r sin t − r sin 2t, 1) .<br />
Parametrické rovnice hledané epicykoidy jsou<br />
x = 2r cos t − r cos 2t , y = 2r sin t − r sin 2t , t ∈ 〈0, 2π) .<br />
Výsledná epicykloida je zobrazena na obr. 9.4.<br />
□<br />
Obrázek 9.3: Obrázek 9.4:<br />
9.1.2 Elipsa<br />
Elipsa o středu O s osami v souřadnicových osách a o poloosách a, b (a > 0, b > 0) má<br />
vektorovou rovnici<br />
X(t) = (a · cos t, b · sin t), t ∈< 0, 2π). (9.4)<br />
Parametr t je tentokrát úhel, jenž je vyznačen v obr. 9.5. Ze vztahů (9.4) a z obr. 9.5 plyne<br />
tzv. trojúhelníková konstrukce bodů elipsy. Strana X b X trojúhelníku X a X b X je rovnoběžná<br />
s osou x a strana X a X tohoto trojúhelníku je rovnoběžná s osou y.<br />
Rozepíšeme-li vztah (9.4) do složek, dostaneme parametrické vyjádření<br />
x = a · cos t , y = b · sin t. (9.5)<br />
Po zřejmé úpravě rovnic (9.5), jejich umocnění a sečtení, dojdeme k rovnici elipsy ve tvaru<br />
x 2<br />
a + y2<br />
= 1. (9.6)<br />
2 b2
9.1. VYJÁDŘENÍ KŘIVEK 80<br />
Podobně jako v případě kružnice lze ukázat, že <strong>pro</strong> elipsu se středem S[m, n] a poloosami<br />
a > 0, b > 0 na rovnoběžkách se souřadnicovými osami platí<br />
9.1.3 Parabola<br />
(x − m) 2 (y − n)2<br />
+ = 1. (9.7)<br />
a 2 b 2<br />
Parabola souměrná podle osy y, která má vrchol v počátku O a ohnisko F [ 0, 2] p , p > 0,<br />
má vektorovou rovnici<br />
(<br />
X(t) = t, 1 )<br />
2p · t2 , t ∈ R. (9.8)<br />
Za parametr t je zvolena souřadnice x bodu paraboly (obr. 9.6).<br />
Snadno z (9.8) dojdeme k vyjádření paraboly ve tvaru<br />
y = 1<br />
2p x2 , resp. x 2 = 2p y . (9.9)<br />
Pro parabolu s vrcholem V [m, n] a osou v rovnoběžce se souřadnicovou osou y můžeme<br />
psát<br />
(y − n) = 1<br />
2p (x − m)2 , resp. (x − m) 2 = 2p (y − n) . (9.10)<br />
Příklad 39. Parabolu o rovnici y = x 2 posuneme tak, aby měla vrchol v bodě V [2, 1],<br />
a určíme společné body posunuté paraboly s přímkou p = AB, kde A[0, 1], B[6, 4].<br />
Řešení: Posunutá parabola k má podle (9.10) rovnici (y − 1) = (x − 2) 2 .<br />
Přímku p vyjádříme parametricky např. ve tvaru<br />
x = 2t , y = 1 + t , t ∈ R . (9.11)<br />
Po dosazení z rovnic (9.11) do rovnice paraboly dostáváme kvadratickou rovnici <strong>pro</strong><br />
parametr t. Platí (1 + t − 1) = (2t − 2) 2 , tj. 4t 2 − 9t + 4 = 0. Řešení této kvadratické<br />
rovnice je tvaru<br />
t 12 = 9 ± √ 17<br />
.<br />
8<br />
Dosazením za t do rovnice (9.11) určíme dva průsečíky X a Y paraboly k a přímky p.<br />
Platí<br />
[<br />
9 + √ 17<br />
X , 17 + √ ] [<br />
17 9 − √ 17<br />
, Y , 17 − √ ]<br />
17<br />
.<br />
4 8<br />
4 8<br />
□
9.1. VYJÁDŘENÍ KŘIVEK 81<br />
9.1.4 Hyperbola<br />
Obrázek 9.5: Obrázek 9.6:<br />
Vektorové vyjádření hyperboly (obr. 9.8) lze uvést ve tvaru (osy hyperboly leží v souřadnicových<br />
osách; a > 0, b > 0)<br />
X(t) = (<br />
a<br />
cos t , b · tg t) , t ∈< 0, 2π) , t ≠ π 2 , 3π<br />
2 . (9.12)<br />
Z těchto vztahů vyplývá konstrukce bodu hyperboly <strong>pro</strong> danou hodnotu parametru t –<br />
viz obr. 9.7.<br />
Z vlastností goniometrických funkcí plyne<br />
1<br />
cos 2 t − tg2 t = 1. (9.13)<br />
Ze vztahů (9.12) a (9.13) vyplývá vyjádření hyperboly ve tvaru<br />
x 2<br />
a − y2<br />
= 1. (9.14)<br />
2 b2 Pro hyperbolu se středem v bodě S[m, n] a s osami na rovnoběžkách se souřadnicovými<br />
osami platí<br />
9.1.5 Obecná rovnice kuželosečky<br />
(x − m) 2 (y − n)2<br />
− = 1. (9.15)<br />
a 2 b 2<br />
Kuželosečkou neboli křivkou druhého stupně rozumíme křivku, kterou lze popsat rovnicí<br />
(indexy i, j u koeficientů a ij jsou odvozeny z exponentů u x a y v daném členu)<br />
a 20 x 2 + 2a 11 xy + a 02 y 2 + 2a 10 x + 2a 01 y + a 00 = 0 , (9.16)
9.1. VYJÁDŘENÍ KŘIVEK 82<br />
Obrázek 9.7: Obrázek 9.8:<br />
kde alespoň jeden z koeficientů a 20 , a 11 , a 02 je nenulový. V maticovém tvaru lze psát<br />
⎛<br />
⎞ ⎛ ⎞<br />
a 20 , a 11 , a 10 x<br />
(x, y, 1) · ⎝ a 11 , a 02 , a 01<br />
⎠ · ⎝ y ⎠ = 0 . (9.17)<br />
a 10 , a 01 , a 00 1<br />
Pro regulární kuželosečku platí, že matice koeficientů v rovnici (9.17) je regulární.<br />
Regulárními kuželosečkami jsou: kružnice, elipsa, parabola a hyperbola.<br />
V předcházejících odstavcích jsme popsali regulární kuželosečky <strong>pro</strong> případ speciálního<br />
umístění (např. střed kružnice, resp. elipsy, resp. vrchol paraboly byl v počátku systému<br />
souřadnic). Pomocí transformace systému souřadnic lze <strong>pro</strong> regulární kuželosečky převést<br />
rovnici kuželosečky z tvaru (9.16) na speciální tvar, tzv. kanonický, který jsme uvedli<br />
v předcházejících odstavcích – tab. 9.1. Pokud je v rovnici (9.16) nenulový koeficient a 11<br />
(koeficient u smíšeného členu), je možné <strong>pro</strong>vést rotaci souřadnicového systému tak, aby<br />
při vyjádření kuželosečky v nové soustavě souřadnic byl tento koeficient nulový. Uved’me<br />
alespoň jeden konkrétní příklad. Obecněji o této věci pojednává odstavec 9.5.
9.1. VYJÁDŘENÍ KŘIVEK 83<br />
Č. Název Signatura Rovnice<br />
1.<br />
Elipsa<br />
x<br />
kružnice <strong>pro</strong> a = b (2,0,0,1) 2<br />
+ y2<br />
= 1<br />
a 2 b 2<br />
2.<br />
3.<br />
4.<br />
5.<br />
6.<br />
7.<br />
8.<br />
9.<br />
Hyperbola<br />
x<br />
záměna <strong>pro</strong>měnných (1,1,0,1) 2<br />
− y2<br />
= 1<br />
a 2 b 2<br />
Parabola<br />
záměna <strong>pro</strong>měnných (1,0,1,0) x 2 ± 2py = 0<br />
Různoběžné přímky<br />
x<br />
záměna <strong>pro</strong>měnných (1,1,0,0) 2<br />
− y2<br />
= 0<br />
a 2 b 2<br />
Rovnoběžné přímky<br />
záměna <strong>pro</strong>měnných (1,0,0,1)<br />
x 2<br />
a 2 = 1<br />
Totožné přímky<br />
záměna <strong>pro</strong>měnných (1,0,0,0) x 2 = 0<br />
Bod<br />
x<br />
záměna <strong>pro</strong>měnných (2,0,0,0) 2<br />
+ y2<br />
= 0<br />
a 2 b 2<br />
Prázdná množina<br />
záměna <strong>pro</strong>měnných (0,2,0,1) − x2 − y2<br />
= 1<br />
a 2 b 2<br />
Prázdná množina<br />
záměna <strong>pro</strong>měnných (0,1,0,1) − x2<br />
a 2 = 1<br />
Tabulka 9.1:
9.1. VYJÁDŘENÍ KŘIVEK 84<br />
Příklad 40. Hyperbolu xy = 1 vyjádříme v systému souřadnic, který vznikne z původního<br />
systému otočením okolo počátku o úhel α = π 4 .<br />
Řešení: Pro transformaci kartézského souřadnicového systému danou rotací o úhel α<br />
platí (obr. 9.9)<br />
x = x ′ · cos α − y ′ · sin α , y = x ′ · cos α + y ′ · sin α . (9.18)<br />
Dosadíme-li do dané rovnice xy = 1 vztahy<br />
(9.18), dostaneme<br />
(x ′·cos α−y ′·sin α)·(x ′·cos α+y ′·sin α) = 1 ,<br />
(9.19)<br />
tj.<br />
x ′2 · cos 2 α − y ′2 · sin 2 α = 1 . (9.20)<br />
Dosadíme cos α = sin α = √ 2<br />
a výsledný tvar<br />
2<br />
rovnice dané hyperboly v kartézské soustavě<br />
souřadnic (O, x ′ , y ′ ) je<br />
x ′ 2<br />
2 − y′ 2<br />
2 = 1 , (9.21)<br />
tj. <strong>pro</strong> poloosy a, b z rovnice (9.14) platí a =<br />
b = √ 2. Obrázek 9.9:<br />
□<br />
V dalším textu budeme předpokládat, že a 11 = 0. Rovnici kuželosečky upravíme na<br />
kanonický tvar<br />
a ⋆ 20(x − s x ) 2 + a ⋆ 02(y − s y ) 2 + a ⋆ 10(x − p x ) + a ⋆ 01(y − p y ) = a ⋆ 00 , (9.22)<br />
kde a ⋆ 00 = 1 nebo a ⋆ 00 = 0 a s x , s y , p x , p y jsou koeficienty, které udávají posunutí kuželosečky.<br />
Převod rovnice kuželosečky (bez smíšeného členu) na kanonický tvar se <strong>pro</strong>vede pomocí<br />
tzv. doplnění kvadratických členů na úplný čtverec. Pro kanonický tvar rovnice kuželosečky<br />
navíc platí:<br />
1. Alespoň jeden z koeficientů a ⋆ 20, a ⋆ 02 je nenulový.<br />
2. Je-li a ⋆ 20 ≠ 0, pak a ⋆ 10 = 0.<br />
3. Je-li a ⋆ 02 ≠ 0, pak a ⋆ 01 = 0.<br />
4. Je-li a ⋆ 10 ≠ 0, pak a ⋆ 00 = 0.<br />
5. Je-li a ⋆ 01 ≠ 0, pak a ⋆ 00 = 0.
9.1. VYJÁDŘENÍ KŘIVEK 85<br />
6. Je-li a ⋆ 00 = 0 a počet záporných koeficientů u kvadratických členů je větší než počet<br />
kladných koeficientů u kvadratických členů, vynásobíme rovnici číslem −1.<br />
Úpravou rovnice kuželosečky na kanonický tvar minimalizujeme počet nenulových koeficientů<br />
v rovnici kuželosečky.<br />
Příklad 41. Je dána kuželosečka k obecnou rovnicí<br />
Určíme kanonický tvar rovnice kuželosečky k.<br />
2x 2 − 4x + 4y + 5 = 0. (9.23)<br />
Řešení: Rovnici (9.23) napíšeme ve tvaru 2(x 2 − 2x) + 4y + 5 = 0 a dvojčlen (x 2 − 2x)<br />
doplníme na úplný čtverec, tj.<br />
Levou stranu rovnice (9.23) lze upravit na tvar<br />
x 2 − 2x = (x − 1) 2 − 1. (9.24)<br />
2x 2 − 4x + 4y + 5 = 2[(x − 1) 2 − 1] + 4y + 5 = 2(x − 1) 2 + 4y + 3 = 0. (9.25)<br />
Výsledný kanonický tvar rovnice dané kuželosečky je<br />
2(x − 1) 2 + 4(y + 3 ) = 0. (9.26)<br />
4<br />
□<br />
Signaturou kuželosečky v kanonickém tvaru (9.22) rozumíme uspořádanou čtveřici čísel<br />
(k, z, l, j), kde<br />
• k, resp. z, udává počet kvadratických členů s kladným, resp. záporným, koeficientem,<br />
• l nabývá hodnoty 0 nebo 1 podle toho, zda po úpravě má rovnice kuželosečky<br />
nenulový koeficient u lineárního členu,<br />
• j nabývá hodnoty 0 nebo 1 podle toho, které z těchto čísel obsahuje pravá strana<br />
upravené rovnice kuželosečky.<br />
Poznamenejme, že <strong>pro</strong> l = 1 je vždy j = 0 a <strong>pro</strong> j = 0 je k ≥ z.<br />
V tab. 9.1 je uvedena klasifikace kuželoseček podle jejich signatur. Je-li u názvu<br />
kuželosečky uvedena poznámka ”<br />
záměna <strong>pro</strong>měnných“, znamená to, že v uvedené rovnici<br />
můžeme vzájemně zaměnit <strong>pro</strong>měnné x a y. Např. zaměníme-li v rovnici paraboly x 2 −y =<br />
0 (osou paraboly je osa y) <strong>pro</strong>měnné, dostaneme parabolu y 2 − x = 0 (osou této paraboly<br />
je osa x).<br />
Příklad 42. Pro kuželosečku z příkladu 41 stanovíme signaturu a typ kuželosečky.<br />
Řešení: Z rovnice (9.26) plyne, že signatura dané kuželosečky je (1,0,1,0). Podle tab. 9.1<br />
se jedná o parabolu. Vrchol V paraboly má souřadnice V [1, − 3 ] a osa o (V ∈ o) paraboly<br />
4<br />
je rovnoběžná s osou y.<br />
□
9.2. VEKTOROVÉ VYJÁDŘENÍ KUŽELOVÝCH A VÁLCOVÝCH PLOCH 86<br />
9.2 Vektorové vyjádření kuželových a válcových ploch<br />
V kartézské soustavě souřadnic v <strong>pro</strong>storu E 3 popíšeme dané plochy vektorovými rovnicemi.<br />
9.2.1 Obecná kuželová plocha<br />
Obecná kuželová plocha je tvořena přímkami, které <strong>pro</strong>cházejí jejím vrcholem V a <strong>pro</strong>tínají<br />
její řídicí křivku k (V ∉ k), která je dána vektorovou funkcí Y (v), v ∈ I v (I v je interval).<br />
Označme Y bod řídicí křivky k kuželové plochy a X obecný bod přímky V Y kuželové<br />
plochy (obr. 9.10). Vektorovou rovnici obecné kuželové plochy lze zapsat ve tvaru<br />
X(u, v) = Y (v) + u(Y (v) − V ) , (9.27)<br />
v níž se vyskytují dva parametry:<br />
v ∈ I v je parametr na křivce k a<br />
u ∈ R je parametr na přímce V X kuželové plochy.<br />
Obrázek 9.10: Obrázek 9.11:<br />
9.2.2 Obecná válcová plocha<br />
Obecná válcová plocha je tvořena přímkami, které mají daný směrový vektor a <strong>pro</strong>tínají<br />
danou řídicí křivku k, danou vektorovou funkcí Y (v), v ∈ I v . Označme s směrový vektor<br />
přímky plochy a Y (t) bod, v němž tato přímka plochy <strong>pro</strong>tíná řídicí křivku k.<br />
Pro polohový vektor X bodu přímky válcové plochy (obr. 9.11) platí<br />
X(u, v) = Y (v) + u · s , (9.28)<br />
kde v ∈ I v je parametr na řídicí křivce k válcové plochy a u ∈ R je parametr na tvořící<br />
přímce válcové plochy.
9.3. ROTAČNÍ PLOCHY DRUHÉHO STUPNĚ (KVADRIKY) V E 3 87<br />
9.3 Rotační plochy druhého stupně (kvadriky) v E 3<br />
Rotační kvadrika vznikne rotací kuželosečky k kolem některé její osy o. Předpokládejme,<br />
že rotující kuželosečka k leží v rovině (xz) a osa kuželosečky, okolo níž kuželosečka rotuje,<br />
splývá s osou z. Kuželosečka k je dána implicitní rovnicí f(x, z) = 0 – viz vztah 9.16.<br />
Uvažujme bod X 0 [x 0 , 0, z 0 ] na dané kuželosečce. Rotací bodu X 0 kolem osy z vzniká<br />
kružnice, <strong>pro</strong> jejíž body M[x, y, z] platí<br />
z = z 0 , x 2 + y 2 = x 2 0 ,<br />
tj. x 0 = ± √ x 2 + y 2 . Dosazením výrazu ± √ x 2 + y 2 za x do rovnice f(x, z) = 0 dostáváme<br />
rovnici rotační kvadriky ve tvaru<br />
f(± √ x 2 + y 2 , z) = 0 . (9.29)<br />
Uvedený obecný postup budeme nyní aplikovat v konkrétních případech.<br />
9.3.1 Kulová plocha<br />
Kulovou plochu vytvoří kružnice o rovnici<br />
x 2 + z 2 − a 2 = 0<br />
při rotaci kolem osy z. Podle (9.29) dostáváme rovnici<br />
x 2 + y 2 + z 2 − a 2 = 0 . (9.30)<br />
Kulová plocha (9.30) je množinou všech bodů v <strong>pro</strong>storu E 3 , které mají od počátku<br />
O danou vzdálenost a > 0.<br />
9.3.2 Rotační elipsoid<br />
Rotační elipsoid vznikne rotací elipsy o rovnici<br />
a + z2<br />
2 b − 1 = 0<br />
2<br />
kolem osy z. Rovnice rotačního elipsoidu je tedy<br />
x 2<br />
x 2<br />
a + y2<br />
2 a + z2<br />
2 b − 1 = 0 . (9.31)<br />
2<br />
Pokud je a > b mluvíme o zploštělém elipsoidu a <strong>pro</strong> a < b o <strong>pro</strong>táhlém elipsoidu. Pro<br />
a = b dostáváme kulovou plochu.<br />
9.3.3 Rotační paraboloid<br />
Rotační paraboloid vytvoříme rotací paraboly o rovnici<br />
x 2 − 2pz = 0<br />
kolem osy z. Rovnice rotačního paraboloidu je tvaru<br />
x 2 + y 2 − 2pz = 0 . (9.32)
9.4. OBECNÁ ROVNICE KVADRIKY 88<br />
9.3.4 Rotační hyperboloid jednodílný<br />
Rotační hyperboloid jednodílný vytvoříme rotací hyperboly o rovnici<br />
x 2<br />
a 2 − z2<br />
b 2 − 1 = 0<br />
kolem osy z, tj. okolo vedlejší osy hyperboly. Dostáváme rovnici<br />
9.3.5 Rotační hyperboloid dvoudílný<br />
x 2<br />
a 2 + y2<br />
a 2 − z2<br />
b 2 − 1 = 0 . (9.33)<br />
Rotační hyperboloid dvoudílný vytvoříme rotací hyperboly okolo její hlavní osy. Uvažujme<br />
<strong>pro</strong>to hyperbolu (hlavní osa hyperboly je v ose z) o rovnici<br />
z 2<br />
a 2 − x2<br />
b 2 − 1 = 0.<br />
Rotací okolo osy z vznikne rotační hyperboloid dvoudílný o rovnici<br />
− x2<br />
b 2 − y2<br />
b 2 + z2<br />
a 2 − 1 = 0 . (9.34)<br />
Obrázek 9.12: Obrázek 9.13:<br />
9.4 Obecná rovnice kvadriky<br />
Pokud uplatníme na rotační kvadriky afinní transformaci dostaneme obecné kvadriky.<br />
Existují však kvadriky, které nejsou odvozeny z rotačních kvadrik (např. hyperbolický
9.4. OBECNÁ ROVNICE KVADRIKY 89<br />
Obrázek 9.14: Obrázek 9.15:<br />
paraboloid). Podobně jako v případě kuželoseček uvedeme obecnou rovnici kvadriky a <strong>pro</strong>vedeme<br />
úplnou diskusi typů kvadrik. K tomu použijeme opět pojem signatura.<br />
Kvadrikou neboli plochou druhého stupně rozumíme plochu, kterou lze popsat rovnicí<br />
(indexy i, j, k u koeficientů a ijk jsou odvozeny z exponentů u x, y a z v daném členu)<br />
a 200 x 2 + a 020 y 2 + a 002 z 2 + 2(a 110 xy + a 101 xz + a 011 yz) + 2(a 100 x + a 010 y + a 001 z) + a 000 = 0 ,<br />
(9.35)<br />
kde alespoň jeden z koeficientů u členů druhého stupně (takových členů je šest) je nenulový.<br />
V maticovém tvaru lze psát<br />
(x, y, z, 1) ·<br />
⎛<br />
⎜<br />
⎝<br />
⎞<br />
a 200 , a 110 , a 101 , a 100<br />
a 110 , a 020 , a 011 , a 010<br />
a 101 , a 011 , a 002 , a 001<br />
a 100 , a 010 , a 001 , a 000<br />
⎟<br />
⎠ ·<br />
⎛<br />
⎜<br />
⎝<br />
x<br />
y<br />
z<br />
1<br />
⎞<br />
⎟<br />
⎠ = 0 . (9.36)<br />
Pro regulární kvadriky platí, že matice koeficientů v rovnici (9.36) je regulární. Regulárními<br />
kvadrikami jsou: kulová plocha, elipsoid (obr. 9.12), eliptický paraboloid (obr. 9.13), hyperbolický<br />
paraboloid (obr. 9.14, 9.15 a 9.16), jednodílný hyperboloid (obr. 9.17) a dvoudílný<br />
hyperboloid (obr. 9.19).<br />
Ze singulárních kvadrik uved’me (kruhovou) kuželovou plochu (obr. 9.20), eliptickou<br />
válcovou plochu (obr. 9.21), parabolickou válcovou plochu 9.20), (obr. 9.22) a hyperbolickou<br />
válcovou plochu (obr. 9.23). 9.20),<br />
Určení kanonického tvaru kvadriky <strong>pro</strong> případ nulových koeficientů u smíšených kvadratických<br />
členů v rovnici kvadriky <strong>pro</strong>vádíme analogickým postupem, jako v případě kuželoseček.<br />
Definice signatury kanonického tvaru rovnice kvadriky a kuželosečky je stejná. Poznamenejme,<br />
že kanonický tvar rovnice kvadriky neobsahuje více než jeden lineární člen (rovněž<br />
tato úprava se dosáhne pomocí transformace systému souřadnic). V tab. 9.2 a 9.3 je<br />
uvedena úplná klasifikace kvadrik.
9.4. OBECNÁ ROVNICE KVADRIKY 90<br />
Obrázek 9.16:<br />
Příklad 43. Rozhodneme, zda kvadrika daná rovnicí<br />
je regulární.<br />
x 2 − 4x + 2y 2 + z + 1 = 0 (9.37)<br />
Řešení: Sestavíme maticový tvar rovnice dané kvadriky – viz rovnice (9.36):<br />
⎛<br />
⎞ ⎛ ⎞<br />
1, 0, 0, −2 x<br />
(x, y, z, 1) · ⎜ 0, 2, 0, 0<br />
⎟<br />
⎝<br />
1<br />
0, 0, 0, ⎠ ·<br />
⎜ y<br />
⎟<br />
⎝ z ⎠ = 0 . (9.38)<br />
2<br />
1<br />
−2, 0, , 1 1<br />
2<br />
Pro matici A řádu 4 ze vztahu (9.38) vypočteme její determinant. Provedeme-li např.<br />
rozvoj podle třetího řádku, zjistíme, že |A| = − 1 . Daná kvadrika je tedy regulární.<br />
2<br />
□<br />
Příklad 44. Stanovíme typ kvadriky dané rovnicí<br />
a určíme její určující prvky (střed, poloosy apod.).<br />
4x 2 − 8x + y 2 − 4y + z 2 + 4 = 0 (9.39)<br />
Řešení: Provedeme doplnění členů (4x 2 − 8x) a (y 2 − 4y) na úplné čtverce. Obdržíme<br />
4x 2 − 8x + y 2 − 4y + z 2 + 4 = (9.40)<br />
= [4(x − 1) 2 − 4] + [(y − 2) 2 − 4] + z 2 + 4 =<br />
= 4(x − 1) 2 + (y − 2) 2 + z 2 − 4 = 0
9.4. OBECNÁ ROVNICE KVADRIKY 91<br />
Obrázek 9.17: Obrázek 9.18:<br />
Kanonický tvar rovnice kvadriky je tudíž<br />
(x − 1) 2 +<br />
(y − 2)2<br />
4<br />
+ z2<br />
4 = 1 .<br />
Signatura dané kvadriky je (3, 0, 0, 1) a podle tab. 9.2 jde o elipsoid. Střed elipsoidu S<br />
má souřadnice S[1, 2, 0] a <strong>pro</strong> poloosy platí a = 1, b = c = 2. Protože dvě poloosy mají<br />
stejnou délku, jde o elipsoid rotační. Osou rotace je rovnoběžka s osou x a <strong>pro</strong>tože je<br />
a < b, jde o elipsoid zploštělý.<br />
□<br />
Příklad 45. Sestavíme rovnici kulové plochy, která se dotýká rovin (xy) a (yz) a má<br />
střed na přímce<br />
o : x = 1 − t , y = 2 + 2t , z = 3 + t , t ∈ R .<br />
Řešení: Nejprve určíme střed S ∈ o hledané kulové plochy. Množinou středů všech<br />
kulových ploch, které se dotýkají daných souřadnicových rovin, jsou dvě roviny σ 1 a σ 2<br />
(při vynechání bodů osy y). Platí<br />
σ 1 : x = z , σ 2 : x = −z .<br />
Snadno stanovíme průsečík S roviny σ 1 s přímkou o. Musí platit 1 − t = 3 + t, tj.<br />
t = −1. Určili jsme střed S[2, 0, 2] hledané kulové plochy. Poloměr r je určen vzdáleností<br />
bodu S od daných souřadnicových rovin, tj. r = 2.<br />
Pro rovinu σ 2 se ukáže, že s přímkou o nemá společný bod, tj. jsou spolu rovnoběžné.
9.4. OBECNÁ ROVNICE KVADRIKY 92<br />
Obrázek 9.19:<br />
Daná úloha má tedy jediné řešení a tím je kulová plocha o rovnici<br />
(x − 2) 2 + y 2 + (z − 2) 2 = 4 ,<br />
neboli<br />
x 2 + y 2 + z 2 − 4x − 4z + 4 = 0 .<br />
□<br />
Příklad 46. Pro kvadriku danou rovnicí (9.37) stanovíme typ kvadriky a její základní<br />
určující prvky. Pak určíme i řezy kvadriky rovinami rovnoběžnými se souřadnicovými<br />
rovinami.<br />
Řešení: Danou rovnici x 2 − 4x + 2y 2 + z + 1 = 0 upravíme na kanonický tvar. Obdržíme<br />
rovnici<br />
(x − 2) 2 + 2y 2 + (z − 3) = 0 . (9.41)<br />
Signatura kvadriky (9.41) je (2,0,1,0), tj. podle tab. 9.2 jde o eliptický paraboloid (není<br />
rotační). Pro vrchol paraboloidu platí V [2, 0, 3]. Osa paraboloidu je rovnoběžná s osou z.<br />
Stanovíme řezy plochy rovinami rovnoběžnými se souřadnicovými rovinami. Uvažujme<br />
nejprve rovinu rovnoběžnou s rovinou (xy), tj. rovinu o rovnici y = y 0 , kde y 0 ∈ R je<br />
konstanta. Řez takovou rovinou má rovnici<br />
(x − 2) 2 + 2y 2 0 + (z − 3) = (x − 2) 2 + (z + 2y 2 0 − 3) = 0 ,<br />
tj. řezy rovinami rovnoběžnými se souřadnicovou rovinou (xz) jsou shodné paraboly.<br />
Podobně řezem rovinou rovnoběžnou s rovinou (yz), tj. rovinou o rovnici x = x 0 , kde<br />
x 0 ∈ R je konstanta, jsou shodné paraboly.
9.4. OBECNÁ ROVNICE KVADRIKY 93<br />
Obrázek 9.20: Obrázek 9.21:<br />
Dále stanovíme řez rovinou z = z 0 , kde z 0 ∈ R je konstanta. Řezem je kuželosečka<br />
o rovnici<br />
(x − 2) 2 + 2y 2 = −(z 0 − 3); .<br />
Pro z 0 < 3 (pak je pravá strana uvedené rovnice kladná) je tedy tímto řezem elipsa.<br />
Ukázali jsme tak, že daný eliptický paraboloid leží pod rovinou z = 3“.<br />
”<br />
□
9.4. OBECNÁ ROVNICE KVADRIKY 94<br />
Obrázek 9.22: Obrázek 9.23:
9.4. OBECNÁ ROVNICE KVADRIKY 95<br />
Č. Název Signatura Rovnice<br />
1.<br />
Elipsoid<br />
kulová plocha . . . a = b = c<br />
rotační elipsoid <strong>pro</strong> dvě čísla stejná<br />
x<br />
(3,0,0,1) 2<br />
+ y2<br />
+ z2 = 1<br />
a 2 b 2 c 2<br />
2.<br />
Hyperboloid jednodílný<br />
rotační <strong>pro</strong> a = b<br />
(osa rotace z, cyklická záměna <strong>pro</strong> další osy)<br />
x<br />
(2,1,0,1) 2<br />
+ y2<br />
− z2 = 1<br />
a 2 b 2 c 2<br />
3.<br />
Hyperboloid dvoudílný<br />
rotační <strong>pro</strong> . . . a = b<br />
(osa rotace z, cyklická záměna <strong>pro</strong> další osy)<br />
(1,2,0,1) − x2<br />
a 2 − y2<br />
b 2 + z2<br />
c 2 = 1<br />
4.<br />
Kuželová plocha<br />
rotační <strong>pro</strong> a = b<br />
(osa rotace z, cyklická záměna <strong>pro</strong> další osy)<br />
x<br />
(2,1,0,0) 2<br />
+ y2<br />
− z2 = 0<br />
a 2 b 2 c 2<br />
5.<br />
Eliptický paraboloid<br />
p > 0, rotační <strong>pro</strong> a = b<br />
(osa rotace z, cyklická záměna <strong>pro</strong> další osy),<br />
znaménko určuje polo<strong>pro</strong>stor z ≤ 0 nebo z ≥ 0 ,<br />
v němž plocha leží<br />
x<br />
(2,0,1,0) 2<br />
+ y2<br />
± z = 0<br />
a 2 b 2 p<br />
6.<br />
Hyperbolický paraboloid<br />
p > 0, cyklická záměna <strong>pro</strong>měnných <strong>pro</strong> další osy,<br />
znaménko určuje orientaci parabol v rovinách xz<br />
a yz<br />
x<br />
(1,1,1,0) 2<br />
− y2<br />
± z = 0<br />
a 2 b 2 p<br />
Tabulka 9.2:
9.4. OBECNÁ ROVNICE KVADRIKY 96<br />
Č. Název Signatura Rovnice<br />
7.<br />
Eliptický válec<br />
rotační <strong>pro</strong> a = b<br />
(osa rotace z, cyklická záměna <strong>pro</strong> další osy)<br />
x<br />
(2,0,0,1) 2<br />
+ y2<br />
= 1<br />
a 2 b 2<br />
8. Hyperbolický válec<br />
cyklická záměna <strong>pro</strong> další osy<br />
x<br />
(1,1,0,1) 2<br />
− y2<br />
= 1<br />
a 2 b 2<br />
9.<br />
Parabolický válec<br />
p > 0, cyklická záměna <strong>pro</strong> další osy,<br />
znaménko určuje polo<strong>pro</strong>stor y ≤ 0 nebo y ≥ 0 ,<br />
v němž plocha leží<br />
(1,0,1,0)<br />
x 2<br />
a 2 ± y p = 0<br />
10. Různoběžné roviny<br />
cyklická záměna <strong>pro</strong>měnných<br />
x<br />
(1,1,0,0) 2<br />
− y2<br />
= 0<br />
a 2 b 2<br />
11. Rovnoběžné roviny<br />
cyklická záměna <strong>pro</strong>měnných<br />
(1,0,0,1)<br />
x 2<br />
a 2 = 1<br />
12. Totožné roviny<br />
záměna <strong>pro</strong>měnných<br />
(1,0,0,0) x 2 = 0<br />
13. Bod – počátek (3,0,0,0)<br />
x 2<br />
a 2<br />
+ y2<br />
b 2<br />
+ z2<br />
c 2 = 0<br />
14.<br />
Přímka – osa z<br />
x<br />
cyklická záměna <strong>pro</strong>měnných (2,0,0,0) 2<br />
+ y2<br />
= 0<br />
a 2 b 2<br />
15.<br />
16.<br />
17.<br />
Prázdná množina<br />
případně záměna <strong>pro</strong>měnných<br />
(0,3,0,1)<br />
(0,2,0,1)<br />
(0,1,0,1)<br />
− x2<br />
a 2 − y2<br />
b 2 − z2<br />
= 1<br />
c 2<br />
− y2<br />
= 1<br />
b 2<br />
= 1<br />
a 2<br />
− x2<br />
a 2<br />
− x2<br />
Tabulka 9.3:
9.5.<br />
KUŽELOSEČKY A KVADRIKY V OBECNÉ POLOZE 97<br />
9.5 Kuželosečky a kvadriky v obecné poloze<br />
V předcházejícím textu jsme uvedli obecné vyjádření kuželoseček – vztah (9.17) a <strong>pro</strong><br />
kvadriky – vztah (9.36). Obecně můžeme napsat obě rovnice ve tvaru<br />
X h · A h · X T h = 0,<br />
kde X h je bod objektu v homogenních souřadnicích a A h je matice dané kuželosečky nebo<br />
kvadriky. Pro potřeby dalšího výpočtu označme A tu část matice A h , která obsahuje<br />
koeficienty u kvadratických členů, tj. <strong>pro</strong> kvadriky platí<br />
⎛<br />
⎞<br />
a 200 , a 110 , a 101<br />
A = ⎝ a 110 , a 020 , a 011<br />
⎠<br />
a 101 , a 011 , a 002<br />
a označme B = (a 100 , a 010 , a 001 ), X = (x, y, z). Obecnou rovnici kvadriky pak můžeme<br />
psát ve tvaru<br />
( ) ( )<br />
A, B<br />
T X<br />
(X, 1) ·<br />
· = 0<br />
B, a 000 1<br />
Určíme odpovídající transformaci daného kvadratického objektu tak, aby po transformaci<br />
byly ve výsledné rovnici nulové koeficienty u smíšených kvadratických členů.<br />
Určujeme tedy matici T h popisující afinní transformaci:<br />
( ) T, 0<br />
T<br />
T h =<br />
,<br />
P, 1<br />
kde T je čtvercová matice řádu 3, P je vektor o třech složkách a 0 je nulový vektor o třech<br />
složkách.<br />
Vzhledem k pravidlu (X · Y) T = Y T · X T <strong>pro</strong> transponování součinu matic obdržíme<br />
( ) ( )<br />
A, B<br />
T<br />
X<br />
(X, 1) · T h ·<br />
· T T h · = 0,<br />
B, a 000 1<br />
tedy po uplatnění asociativity násobení matic a po dosazení<br />
( ) ( )<br />
T · A · T<br />
T<br />
, ˜BT X<br />
(X, 1) ·<br />
· = 0.<br />
˜B , ã 000 1<br />
I když to <strong>pro</strong> další úvahy není podstatné, uved’me, že<br />
˜B = P · A · T T + B · T T (9.42)<br />
ã 000 = P · A · P T + B · P T + P · B T + a 000 .<br />
Dále si všimneme součinu T·A·T T = D. Afinní transformací chceme dosáhnout toho,<br />
aby matice D byla diagonální, to totiž odpovídá právě požadavku, aby v rovnici kvadriky<br />
byly nulové koeficienty u smíšených kvadratických členů. V lineární algebře se dokazuje,
9.5.<br />
KUŽELOSEČKY A KVADRIKY V OBECNÉ POLOZE 98<br />
že k symetrické matici (a matice A je symetrická) existují uvedené matice D a T. Matice<br />
D má za diagonální prvky vlastní čísla matice A a transformační matice T má za řádky<br />
vlastní vektory odpovídající těmto vlastním číslům.<br />
Zcela stejně lze postupovat i v případě vyšetřování kuželoseček. Uvedené vztahy jsme<br />
zapsali maticově, a tak se v případě kuželoseček jen sníží příslušným způsobem rozměry<br />
použitých objektů.<br />
Na druhou stranu jsme neuvedli všechny detaily vyšetřování kvadratických objektů<br />
pomocí vlastních vektorů a vlastních čísel příslušné matice. Jde např. o případ, kdy jsou<br />
dvě vlastní čísla matice stejná. V případě shodných nenulových vlastních čísel matice<br />
kvadriky je kvadrika rotační. Poznamenejme dále, že nulové vlastní číslo dokazuje, že<br />
kvadratický objekt je singulární apod.<br />
Uvedený postup si znovu objasníme na příkladu.<br />
Příklad 47. Určíme typ a základní charakteristiky kvadriky<br />
Řešení: Maticově můžeme psát<br />
⎛<br />
(x, y, z, 1) ·<br />
⎜<br />
⎝<br />
x 2 + 2xy − 2xz = 1.<br />
1, 1, −1, 0<br />
1, 0, 0, 0<br />
−1, 0, 0, 0<br />
0, 0, 0, −1<br />
⎞<br />
⎟<br />
⎠ ·<br />
⎛<br />
⎜<br />
⎝<br />
x<br />
y<br />
z<br />
1<br />
⎞<br />
⎟<br />
⎠ = 0.<br />
Snadno zjistíme, že matice kvadriky je singulární (třetí řádek je násobkem druhého řádku),<br />
tedy půjde o singulární kvadriku.<br />
Určíme vlastní čísla a odpovídající vlastní vektory matice<br />
Sestavíme determinant<br />
a obdržíme rovnici<br />
tj.<br />
⎛<br />
A = ⎝<br />
det(λI − A) =<br />
∣<br />
1, 1, −1<br />
1, 0, 0<br />
−1, 0, 0<br />
⎞<br />
⎠ .<br />
λ − 1, −1, 1<br />
−1, λ, 0<br />
1, 0, λ<br />
λ 2 (λ − 1) − λ − λ = 0,<br />
λ(λ 2 − λ − 2) = 0.<br />
Snadno zjistíme, že vlastní čísla matice A jsou<br />
λ 1 = 0, λ 2 = −1, λ 3 = 2.<br />
Nyní určíme vlastní vektory matice A odpovídající vypočteným vlastním číslům.<br />
Zároveň vlastní vektory znormujeme. Určení vlastních vektorů <strong>pro</strong>vedeme řešením soustav<br />
A · (x, y, z) T = λ i · (x, y, z) T , i = 1, 2, 3.<br />
∣
9.6. CVIČENÍ 99<br />
Jedná se tedy o homogenní soustavy s maticemi<br />
⎛<br />
2, 1,<br />
⎞<br />
−1<br />
⎛<br />
V 1 = A, V 2 = ⎝ 1, 1, 0 ⎠ , V 3 = ⎝<br />
−1, 0, 1<br />
Normovanými vlastními vektory jsou např. vektory<br />
√ √<br />
2<br />
3<br />
v 1 =<br />
2 (0, 1, 1), v 2 =<br />
3 (1, −1, 1), v 3 =<br />
−1, 1, −1<br />
1, −2, 0<br />
−1, 0, −2<br />
√<br />
6<br />
(−2, −1, 1).<br />
6<br />
Snadno sestavíme matice T h a vyjádříme kvadriku v souřadnicové soustavě (O, v 1 , v 2 , v 3 ).<br />
Platí<br />
⎛<br />
√<br />
0, 2<br />
, √ ⎞<br />
2<br />
, 0 ⎛<br />
⎞<br />
2 2 1, 1, −1, 0<br />
√<br />
T h · A h · T T 3<br />
h = ⎜<br />
, − √ 3<br />
, √<br />
3<br />
, 0<br />
3 3 3<br />
⎝ − √ 6<br />
, − √ 6<br />
, √<br />
6<br />
, 0 ⎟<br />
⎠ ·<br />
⎜ 1, 0, 0, 0<br />
⎟<br />
⎝ −1, 0, 0, 0 ⎠ ·<br />
3 6 6<br />
0, 0, 0, 1 0, 0, 0, −1<br />
⎛<br />
√<br />
0, 3<br />
, − √ ⎞<br />
6<br />
, 0 ⎛<br />
⎞<br />
3 3 0, 0, 0, 0<br />
√ 2<br />
· ⎜<br />
, − √ 3<br />
, − √ 6<br />
, 0<br />
√2 3 6<br />
⎝ 2<br />
, √<br />
3<br />
, √<br />
6<br />
, 0 ⎟<br />
⎠ = ⎜ 0, −1, 0, 0<br />
⎟<br />
⎝ 0, 0, 2, 0 ⎠ .<br />
2 3 6<br />
0, 0, 0, 1 0, 0, 0, −1<br />
Kanonický tvar rovnice dané kvadriky po transformaci souřadnic je<br />
−ỹ 2 + 2˜z 2 = 1.<br />
Jde o hyperbolickou válcovou plochu s řídící hyperbolou v rovině určené počátkem a vektory<br />
v 2 a v 3 .<br />
□<br />
⎞<br />
⎠<br />
9.6 Cvičení<br />
9.1 Kružnice má rovnici x 2 + y 2 − 2x + 4y − 20 = 0. Napište její vektorovou rovnici.<br />
[r(t) = (1 + 5 cos t, −2 + 5 sin t), t ∈ 〈0, 2π)]<br />
9.2 Napište vektorovou rovnici, resp. parametrické rovnice elipsy, která má střed S[2, −1]<br />
a poloosy a = 3, b = 2. Její hlavní osa je rovnoběžná s osou x.<br />
[r(t) = (2 + 3 cos t, −1 + 2 sin t), t ∈ 〈0, 2π)]<br />
9.3 Eliminujte parametr t z parametrických rovnic paraboly x = 3t, y = 4t−5t 2 , t ∈ R.<br />
[y = 4 3 x − 5 9 x2 ]<br />
9.4 Odvod’te parametrické rovnice obyčejné cykloidy, kterou opisuje bod kružnice odvalující<br />
se po přímce. Poloměr této kružnice je r. [x = r(t − sin t), y = r(1 − cos t), t ∈ R]
9.6. CVIČENÍ 100<br />
9.5 Odvalováním přímky po křivce k vzniká jako dráha bodu tzv. evolventa dané křivky<br />
k. Sestavte parametrické rovnice evolventy kružnice o poloměru r.<br />
[x = r(cos t + t sin t), y = r(sin t − t cos t), t ∈ R]<br />
9.6 Vypočtěte souřadnice bodů s parametry t = 0, π, π, 3π , π ležících na křivce r(t) =<br />
4 2 4<br />
( √ 2 cos t, √ 2 cos t, 2 sin t).<br />
[[ √ 2, √ 2, 0], [1, 1, √ 2], [0, 0, 2], [−1, −1, √ 2], [− √ 2, − √ 2, 0]]<br />
9.7 Napište vektorovou a implicitní rovnici rotační kuželové plochy, která má vrchol<br />
v počátku a její řídicí kružnice o rovnici x 2 + y 2 = a 2 leží v rovině z = 1.<br />
[r(u, v) = (av cos u, av sin u, v), u ∈ 〈0, 2π), v ∈ R, x 2 + y 2 − a 2 z 2 = 0]<br />
9.8 Napište vektorovou a implicitní rovnici kuželové plochy o vrcholu V v počátku O,<br />
jejíž řídicí křivka k je elipsa o vektorové rovnici r(t) = (a cos t, b sin t, 1), a > 0, t ∈<br />
〈0, 2π).<br />
x<br />
[r(t, v) = (av cos t, bv sin t, v), v ∈ R, 2<br />
+ y2<br />
− z 2 = 0]<br />
a 2 b 2<br />
9.9 Napište vektorovou a implicitní rovnici válcové plochy, jejíž řídicí parabola o rovnici<br />
y 2 −4x = 0 leží v rovině z = 0 a její přímky mají směr určený vektorem s = (1, 2, 3).<br />
[r(t, v) = ( t2 4 + v, t + 2v, 3v), t ∈ R, v ∈ R, 9y2 + 4z 2 − 12yz − 36x + 12z = 0]<br />
9.10 Kružnice k leží v rovině y = 0 a má rovnici (x − b) 2 + z 2 = a 2 . Při otáčení kolem<br />
osy z vytvoří plochu, jíž říkáme anuloid. Napište implicitní rovnici této plochy.<br />
[4b 2 (x 2 + y 2 ) = (x 2 + y 2 + z 2 + b 2 − a 2 ) 2 ]<br />
9.11 Napište vektorovou rovnici kulové plochy o středu S a poloměru a. [|X − S| = a]<br />
9.12 Rotační elipsoid má implicitní rovnici<br />
x 2<br />
a 2 + y2<br />
a 2 + z2<br />
b 2 − 1 = 0 .<br />
Sestavte jeho parametrické rovnice při použití sférických souřadnic.<br />
[x = a cos ϕ cos ψ, y = a sin ϕ cos ψ, z = b sin ψ, a > 0, b > 0,<br />
ϕ ∈ 〈0, 2π), ψ ∈ ( − π 2 , π 2<br />
)<br />
]<br />
9.13 Ukažte, že všechny roviny rovnoběžné s osou z <strong>pro</strong>tínají kvadriku o rovnici x 2 +y 2 −<br />
z = 0 ve shodných parabolách.<br />
Návod: Ukažte, že jde o rotační paraboloid a uvažujte řezy rovinami y =konst.<br />
9.14 Ukažte, že rotací přímky p, která je mimoběžná s osou rotace a není k ní kolmá,<br />
vznikne jednodílný rotační hyperboloid.<br />
Návod: Osu rotace volte v ose z a přímku p o směrnici b v rovině x = a. [viz<br />
a<br />
( 9.33)]<br />
9.15 Určete typ kvadriky 4x 2 + y 2 − 4z 2 − 16x − 2y + 21 = 0. Zjistěte její určující prvky.<br />
[dvoudílný (nerotační) hyperboloid; střed S[2, 1, 0]]<br />
9.16 Určete typ kvadriky 2x 2 − 3y 2 − 8x + 12y + 10 = 0.<br />
[hyperbolická válcová plocha]
9.7. KONTROLNÍ OTÁZKY 101<br />
9.17 Určete typ kvadriky 4y 2 + z 2 + x + 16y − 3 = 0. Zjistěte její určující prvky.<br />
[eliptický (nerotační) paraboloid; vrchol V [19, −2, 0], osa rovnoběžná s osou x, řezy<br />
rovinami x = x 0 , x 0 < 19, jsou elipsy]<br />
9.18 Určete typ kvadriky −4x 2 + 9y 2 + 36z = 0 a stanovte řezy rovinami y = λx, λ ∈ R.<br />
[hyperbolický paraboloid; řezem je <strong>pro</strong> λ ≠ ± 2 parabola, <strong>pro</strong> λ = ± 2 jsou řezem<br />
3 3<br />
přímky]<br />
9.7 Kontrolní otázky<br />
9.1 Kolika jednoduchými podmínkami, tj. např. kolika obecnými body, je určena kuželosečka?<br />
(Návod: Určete počet volitelných koeficientů v obecné rovnici kuželosečky.)<br />
9.2 Vyjmenujte rotační kvadriky.<br />
9.3 Kolika jednoduchými podmínkami, tj. např. kolika obecnými body, je určena kvadrika?<br />
(Návod: Určete počet volitelných koeficientů v obecné rovnici kvadriky.)<br />
9.4 Vysvětlete pojem kanonický tvar rovnice kvadriky (kuželosečky).<br />
9.5 Uved’te metody, kterými je možné upravit obecnou rovnici kvadriky na kanonický<br />
tvar.<br />
9.6 Matice kuželosečky má vlastní čísla λ 1 = 2, λ 2 = 3. O jakou kuželosečku jde?<br />
(Návod: Jsou dvě možnosti.)<br />
9.7 Matice kvadriky má vlastní čísla λ 1 = 1, λ 2 = −1, λ 3 = 2. O jakou kvadriku jde?<br />
(Návod: Jsou dvě možnosti.)
Literatura<br />
[1] Bohne, E. – Klix, W.D.: <strong>Geometrie</strong> – Grundlagen für Anwendungen. Leipzig, Fachbuchverlag<br />
1995.<br />
[2] Ježek, F. – Míková, M.: Maticová algebra a analytická geometrie. Plzeň, ZČU 2003.<br />
[3] Rogers, D.F. – Adams, J.A.: Mathematical Elements for Computer Graphics. New<br />
York, Mc Graw–Hill 1990.<br />
[4] Urban, A.: Deskriptivní geometrie I. Praha, SNTL 1965.<br />
[5] Urban, A.: Deskriptivní geometrie II. Praha, SNTL 1967.<br />
102
Rejstřík<br />
Afinní transformace, 12<br />
Archimédova serpentina, 52, 60<br />
Asymptota<br />
křivky, 21<br />
Bod<br />
charakteristický, 25<br />
inflexní, 22<br />
uzlový, 22<br />
vratu, 22<br />
Charakteristika<br />
kulové plochy, 59<br />
obalové plochy, 56<br />
roviny, 57<br />
Cykloida, 26<br />
<strong>pro</strong>dloužená, 26<br />
<strong>pro</strong>stá, 26<br />
zkrácená, 26<br />
Dilatace, 12<br />
Doplnění na úplný čtverec, 84<br />
Dráha bodu, 26<br />
Ekvidistanta<br />
křivky, 26<br />
Elipsa<br />
parametrické vyjádření, 79<br />
vektorové vyjádření, 79<br />
Elipsoid<br />
<strong>pro</strong>táhlý, 91<br />
rotační, 87, 91<br />
zploštělý, 91<br />
Epicykloida, 78<br />
Evoluta<br />
křivky, 26<br />
Evolventa<br />
křivky, 26<br />
kruhová, 69<br />
Flexe, 23<br />
Gaussova křivost plochy, 38<br />
Globoid, 44<br />
Hlavní normála, 23<br />
Hyperbola<br />
parametrické vyjádření, 81<br />
vektorové vyjádření, 81<br />
Hyperboloid<br />
dvojdílný rotační, 44<br />
jednodílný rotační, 44<br />
rotační<br />
dvoudílný, 88<br />
jednodílný, 88<br />
Identita, 13<br />
Inverzní transformace, 13<br />
Křivka, 20, 21<br />
asymptota, 21<br />
definice, 20<br />
konstantního spádu, 28<br />
na ploše, 35<br />
parametrická, 35<br />
normála, 21<br />
parametrické rovnice, 21<br />
průniková, 35<br />
regulární, 20<br />
rektifikace, 22<br />
rovinná, 21<br />
sečna, 21<br />
tečna, 21<br />
tvořící, 41<br />
vektorový popis, 21<br />
Křivost<br />
druhá, 23<br />
Gaussova, 38<br />
první, 23<br />
103
REJSTŘÍK 104<br />
Komplanace (rozvinutí), 69<br />
tečna křivky, 71<br />
Kroneckerovo delta, 7<br />
Kružnice<br />
hrdlová, 43<br />
kráterová, 43<br />
oskulační, 23<br />
parametrické vyjádření, 77<br />
rovníková, 43<br />
rovnoběžková, 41<br />
vektorové vyjádření, 77<br />
Kruhová evolventa, 69<br />
Kuželosečka<br />
kanonický tvar rovnice, 84<br />
obecná rovnice, 81<br />
regulární, 82<br />
signatura, 85<br />
Kuželová plocha<br />
řídící, 26<br />
Kulová plocha, 87<br />
Kvadrika<br />
kanonický tvar rovnice, 89<br />
obecná rovnice, 88<br />
regulární, 89<br />
rotační, 47, 87<br />
regulární, 47<br />
singularní, 47<br />
singulární, 89<br />
Meridián, 41, 50<br />
hlavní, 41<br />
Metoda<br />
kulových ploch, 60, 61<br />
normálového řezu, 69<br />
tečných rovin, 60, 63<br />
triangulace, 70<br />
Normála<br />
hlavní, 23<br />
křivky, 21<br />
plochy, 35<br />
Normálová rovina<br />
křivky, 21<br />
Normálový<br />
řez, 38<br />
Obálka, 25<br />
Obalová křivka, 25<br />
Obalová plocha, 56<br />
výpočet, 65<br />
Obrys plochy, 36<br />
Oskulační<br />
kružnice, 23<br />
rovina, 23<br />
Osová souměrnost, 11<br />
Otáčení (rotace), 14<br />
okolo bodu, 11<br />
Příčný <strong>pro</strong>fil, 50<br />
Přímka na ploše<br />
regularní, 35<br />
torzální, 35<br />
Parabola<br />
parametrické vyjádření, 80<br />
vektorové vyjádření, 80<br />
Paraboloid<br />
eliptický, 92<br />
hyperbolický, 95<br />
rotační, 87<br />
Parametrické vyjádření<br />
plochy, 34<br />
Plocha<br />
šroubová, 50<br />
Archimédova serpentina, 52<br />
cyklická, osová, 52<br />
meridián, 50<br />
přímková, 52<br />
přímková, kosoúhlá, 52<br />
přímková, otevřená, 52<br />
přímková, pravoúhlá, 52<br />
přímková, uzavřená, 52<br />
parametrické vyjádření, 50<br />
polomeridián, 50<br />
rozvinutelná, 52<br />
vinutý sloupek, 52<br />
definice, 33<br />
explicitní vyjádření, 35<br />
implicitní vyjádření, 35<br />
kuželová (obecná), 69, 86<br />
kulová, 87<br />
normála, 35
REJSTŘÍK 105<br />
obalová, 56<br />
obrys, 36<br />
přechodová, 72<br />
parametrické vyjádření, 34<br />
regulární, 33<br />
rotační, 41<br />
řez, 45<br />
anuloid, 44<br />
dvojdílný hyperboloid, 44<br />
elipsoid, 44<br />
globoid, 44<br />
jednodílný hyperboloid, 44<br />
kvadrika, 47<br />
paraboloid, 44<br />
průnik, 47<br />
rozvinutelná, 68<br />
tečen <strong>pro</strong>storové křivky, 69<br />
tečná rovina, 35<br />
tvořící, 56<br />
válcová<br />
eliptická, 89<br />
hyperbolická, 89<br />
parabolická, 89<br />
válcová (obecná), 69, 86<br />
vývrtková, 52<br />
Pohyb<br />
šroubový, 27<br />
Poledník, 41<br />
Poloměr<br />
křivosti, 23<br />
Polomeridián, 50<br />
Posunutí (translace), 14<br />
Površka<br />
regularní, 35<br />
torzální, 35, 68<br />
Průnik<br />
rotačních kvadrik<br />
rozpad, 48<br />
rotačních ploch, 47<br />
Redukovaná výška závitu, 27<br />
Rektifikace křivky, 22<br />
Rotace<br />
okolo bodu, 11<br />
Rotace (otáčení), 14<br />
Rovina<br />
oskulační, 23<br />
Rozpad průniku rotačních kvadrik, 48<br />
Rozvinutí, 69<br />
Rozvinutelná šroubová plocha, 52<br />
Rozvinutelná plocha šroubová<br />
rozvinutí, 71<br />
Řídící kužel<br />
šroubovice, 29<br />
Řez<br />
čelní, 50<br />
na rotační ploše, 45<br />
normálový, 38, 69<br />
Sečna<br />
křivky, 21<br />
Skládání transformací, 13, 16<br />
Souřadnice<br />
afinní, 9, 74<br />
cylindrické, 74<br />
homogenní, 10<br />
kartézské, 74<br />
sférické, 74<br />
Souměrnost<br />
podle osy, 11<br />
podle roviny, 15<br />
Střed<br />
křivosti, 23<br />
Šroubový pohyb, 27<br />
Šroubovice, 27<br />
křivosti, 29<br />
levotočivá, 27<br />
parametrické vyjádření, 27<br />
pravotočivá, 27<br />
Tečná křivky v rozvinutí, 71<br />
Tečna<br />
křivky, 21<br />
Torze, 23<br />
Trajektorie bodu, 26<br />
Transformace, 6<br />
afinní, 12, 15<br />
inverzní, 13<br />
skládání, 13, 16
REJSTŘÍK 106<br />
Translace (posunutí), 14<br />
Tvořící plocha, 56<br />
Úhel křivek, 21<br />
Válcová plocha<br />
eliptická, 89<br />
hyperbolická, 89<br />
parabolická, 89<br />
Výška závitu, 27<br />
redukovaná, 27<br />
Vývrtková plocha, 52<br />
Věta<br />
o obalové ploše, 65<br />
o typech rozvinutelných ploch, 68<br />
Vinutý sloupek, 52<br />
Změna měřítka, 12