Deskriptivn´ı geometrie 1

Západočeská univerzita v PlzniFakulta aplikovaných vědKatedra matematikyDeskriptivní geometrie 1Pomocný učební text1. částSvětlana TomiczkováPlzeň – 22. září 2009– verze 2.0

PředmluvaTento pomocný text vznikl pro potřeby předmětu Deskriptivní geometrie I. Některé části jsoushodné s kapitolami ve skriptech pro strojní fakultu, které jsme vytvořili společně s doc. RNDr.Františkem Ježkem CSc.Chybí zde ještě pojednání o kótovaném promítání, řešení terénu a kartografických projekcích.Pokud najdete v textu nedopatření, resp. pokud je text někde nesrozumitelný, prosímo sdělení takových poznatků. Ideální cestou je použití e-mailu a adresy svetlana@kma.zcu.cz.Autorka2

Obsah1 Opakování stereometrie 61.1 Axiómy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61.2 Určování odchylek . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61.2.1 Odchylka mimoběžek . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71.2.2 Odchylka dvou rovin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71.3 Kritéria rovnoběžnosti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71.4 Kritéria kolmosti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81.5 Otáčení v prostoru . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81.6 Dělící poměr . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91.7 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102 Nevlastní elementy 112.1 Úvodní úvaha . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112.2 Nevlastní bod, přímka a rovina . . . . . . . . . . . . . . . . . . . . . . . . . . . 112.3 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123 Kuželosečky 133.1 Úvod . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133.2 Elipsa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133.2.1 Rovnice elipsy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143.2.2 Proužková konstrukce elipsy . . . . . . . . . . . . . . . . . . . . . . . . . 153.2.3 Oskulační kružnice elipsy . . . . . . . . . . . . . . . . . . . . . . . . . . . 153.2.4 Rytzova konstrukce . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163.2.5 Tečna a ohniskové vlastnosti elipsy . . . . . . . . . . . . . . . . . . . . . 173.3 Hyperbola . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193.3.1 Tečna a ohniskové vlastnosti hyperboly . . . . . . . . . . . . . . . . . . . 203.4 Parabola . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203.4.1 Tečna a ohniskové vlastnosti paraboly . . . . . . . . . . . . . . . . . . . 213.5 Pascalova a Brianchonova věta . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223.6 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264 Elementární plochy a tělesa 284.1 Základní pojmy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 284.1.1 Jehlanová plocha, jehlan . . . . . . . . . . . . . . . . . . . . . . . . . . . 284.1.2 Hranolová plocha, hranol . . . . . . . . . . . . . . . . . . . . . . . . . . . 283

Obsah 44.1.3 Kuželová plocha, kužel . . . . . . . . . . . . . . . . . . . . . . . . . . . . 294.1.4 Válcová plocha, válec . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304.1.5 Kulová plocha, koule . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304.2 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305 Základy promítání 315.1 Úvod . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315.2 Středové promítání . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315.3 Rovnoběžné promítání . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 325.4 Pravoúhlé promítání . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335.5 Středová kolineace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335.6 Osová afinita . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 375.7 Kružnice v osové afinitě a středové kolineaci . . . . . . . . . . . . . . . . . . . . 395.8 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 406 Mongeovo promítání 426.1 Úvod . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 426.2 Obraz bodu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 426.3 Obraz přímky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 436.4 Obraz roviny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 456.5 Polohové úlohy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 486.5.1 Přímka v rovině (základní úloha Z1) . . . . . . . . . . . . . . . . . . . . 486.5.2 Bod v rovině (základní úloha Z2) . . . . . . . . . . . . . . . . . . . . . . 516.5.3 Rovnoběžné roviny (základní úloha Z3) . . . . . . . . . . . . . . . . . . . 536.5.4 Průsečík přímky s rovinou (základní úloha Z4) . . . . . . . . . . . . . . . 546.5.5 Průsečnice dvou rovin (základní úloha Z5) . . . . . . . . . . . . . . . . . 566.6 Metrické úlohy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 586.6.1 Skutečná velikost úsečky (základní úloha Z6) . . . . . . . . . . . . . . . . 586.6.2 Nanesení úsečky na přímku (základní úloha Z7) . . . . . . . . . . . . . . 606.6.3 Přímka kolmá k rovině (základní úloha Z8) . . . . . . . . . . . . . . . . . 606.6.4 Rovina kolmá k přímce (základní úloha Z9) . . . . . . . . . . . . . . . . 626.6.5 Otočení roviny do polohy rovnoběžné s průmětnou (základní úloha Z10) . 636.6.6 Obraz kružnice (základní úloha Z11) . . . . . . . . . . . . . . . . . . . . 666.6.7 Transformace průměten (základní úloha Z12) . . . . . . . . . . . . . . . 676.7 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 687 Axonometrie 697.1 Úvod . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 697.2 Klasifikace axonometrií . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 707.3 Zobrazení bodu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 717.4 Zobrazení přímky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 727.5 Zobrazení roviny . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 737.6 Úlohy v axonometrii . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 747.6.1 Vzájemná poloha přímek . . . . . . . . . . . . . . . . . . . . . . . . . . . 747.6.2 Přímka v rovině . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74

Obsah 57.6.3 Průsečík přímky s rovinou . . . . . . . . . . . . . . . . . . . . . . . . . . 767.6.4 Průsečnice rovin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 777.6.5 Kružnice v souřadnicové rovině . . . . . . . . . . . . . . . . . . . . . . . 787.7 Pravoúhlá axonometrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 797.7.1 Metrické úlohy v rovinách xy, yz, zx . . . . . . . . . . . . . . . . . . . . 797.7.2 Obraz kružnice ležící v některé souřadnicové rovině . . . . . . . . . . . . 817.8 Kontrolní otázky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83

Kapitola 1Opakování stereometrieNa úvod připomeneme základní pojmy a věty z prostorové geometrie, které budeme používatv dalších kapitolách.1.1 AxiómyAxiómy jsou jednoduchá tvrzení, která nemůžeme dokázat. Z nich se potom odvozují další věty.Tento systém axiómů použil před více než 2000 lety slavný řecký geometr Euklides k vybudováníprostorové geometrie. Geometrii vybudované na tomto systému axiómů říkáme Euklidovskágeometrie.Uvedeme si pět základních axiómů prostorové geometrie:1. axióm: Dva různé body A, B určují právě jednu přímku p. Symbolicky tuto větu zapíšeme:∀A, B; A ≠ B ∃! p = AB.2. axióm: Přímka p a bod A, který neleží na přímce p, určují právě jednu rovinu α. Symbolicky:∀A, p; A /∈ p ∃! α = (A, p).3. axióm: Leží-li bod A na přímce p a přímka p v rovině α, leží i bod A v rovině α. Symbolicky:∀A, p, α; A ∈ p ∧ p ⊂ α ⇒ A ∈ α.4. axióm: Mají-li dvě různé roviny α, β společný bod P , pak mají i společnou přímku p a Pleží na p. Symbolicky: ∀α, β, α ≠ β : P ∈ α ∩ β ⇒ ∃! p : P ∈ p ∧ α ∩ β = p.5. axióm: Ke každé přímce p lze bodem P , který na ní neleží, vést jedinou přímku p ′ rovnoběžnous p. Symbolicky: ∀P, p : P /∈ p ⇒ ∃! p ′ : p ′ ||p ∧ P ∈ p ′ .Uvedených pět axiómů tvoří základ, ale museli bychom je doplnit o další axiómy, aby systémdovoloval vybudování klasické geometrie. Není však cílem tohoto textu uvést úplný přehledaxiómů a vět prostorové geometrie. Zaměříme se jen na takové vztahy, které budeme přímovyužívat v dalším výkladu.1.2 Určování odchylekV rovině umíme určit odchylku přímek, které jsou různoběžné. Protože se zabýváme prostorovýmivztahy, nadefinujeme si i odchylku dvou mimoběžek a ukážeme si, jak lze určit odchylkudvou rovin.6

1.3. Kritéria rovnoběžnosti 71.2.1 Odchylka mimoběžek1. V prostoru jsou dány dvě mimoběžky a,b.2. Libovolným bodem M vedeme přímku a ′rovnoběžnou s přímkou a a přímku b ′ rovnoběžnous přímkou b.3. Odchylka mimoběžek a, b je rovna odchylcepřímek a ′ , b ′ . Obrázek 1.1:1.2.2 Odchylka dvou rovinUvedeme dva způsoby, jak určit odchylku dvou různoběžných rovin α a β.1. způsob - obr. 1.2Obrázek 1.2: Obrázek 1.3:1. Sestrojíme průsečnici p rovin α a β.2. Sestrojíme rovinu γ kolmou na p.3. Sestrojíme průsečnici a rovin α a γ a průsečnici b rovin β a γ.4. Odchylka ϕ přímek a, b je odchylkou rovin α a β.2. způsob - obr. 1.31. Libovolným bodem M vedeme kolmici n k rovině α.2. Stejným bodem M vedeme kolmici n ′ k rovině β.3. Odchylka přímek n, n ′ je odchylkou rovin α a β.1.3 Kritéria rovnoběžnostiVěta 1.1 Kritérium rovnoběžnosti přímky s rovinou. Přímka p je rovnoběžná s rovinouα, právě když existuje přímka p ′ ležící v rovině α, rovnoběžná s přímkou p – obr. 1.4.

1.4. Kritéria kolmosti 8Věta 1.2 Kritérium rovnoběžnosti dvou rovin. Rovina α je rovnoběžná s rovinou β,právě když existují různoběžky a, b ležící v rovině α a rovnoběžné s rovinou β – obr. 1.5.Obrázek 1.4: Obrázek 1.5:1.4 Kritéria kolmostiVěta 1.3 Kritérium kolmosti přímky a roviny. Přímka p je kolmá k rovině α, jestližeje kolmá ke dvěma různoběžkám a, b ležícím v rovině α – obr. 1.6.Věta 1.4 Kritérium kolmosti dvou rovin. Rovina α je kolmá k rovině β, jestliže v roviněα existuje přímka p kolmá k rovině β (tj. kolmá ke dvěma různoběžkám a, b ležícím v rovině β)– obr. 1.7.Obrázek 1.6: Obrázek 1.7:1.5 Otáčení v prostoruTransformacím bude věnována celá kapitola. Nyní si pouze připomeneme základní vlastnostiotáčení (rotace), protože otáčení budeme potřebovat při studiu zobrazovacích metod.

1.6. DělÍcÍ poměr 9Popíšeme otáčení v prostoru okolo osy o o úhel ϕ. Body osy otáčení jsou samodružné (zobrazíse samy na sebe). Bod A se otáčí po kružnici k. Určíme střed S kružnice k, poloměr ra rovinu ρ, ve které kružnice k leží - obr. 1.8.• Rovina otáčení ρ prochází bodem A a je kolmá k ose otáčení o.• Střed otáčení S je průsečíkem osy o s rovinou ρ.• Poloměr otáčení r je velikost úsečky AS, píšeme r = |AS|.Obrázek 1.8: Obrázek 1.9:Příklad 1.1 Jsou dány různoběžné roviny α a π, v rovině α je dán bod A. Napíšeme postuppro otočení bodu A do roviny π - obr. 1.9.Řešení:1. Osou otáčení o je průsečnice rovin α a π (o = α ∩ π).2. Rovina otáčení ρ je kolmá k ose o a prochází bodem A (ρ ⊥ o ∧ A ∈ ρ).3. Střed otáčení S získáme jako průsečík osy o a roviny ρ (S = o ∩ ρ).4. Velikost úsečky SA je poloměr otáčení (r = |SA|).□1.6 Dělící poměrNa orientované přímce p jsou dány dva různé body A, B. Bod C ≠ B je libovolný bod přímkyp. Dělící poměr bodu C vzhledem k bodům A, B je čísloλ = (A, B, C) = d( −→ AC) : d( −→ BC),kde d( −→ AC), d( −→ BC) jsou orientované délky příslušných úseček.Například je-li bod C středem úsečky AB, jeho dělící poměr vzhledem k bodům A, B jeλ = −1, což plyne ze vztahu d( −→ AC) = −d( −→ BC).Obráceně ke každému číslu λ ≠ 1 můžeme sestrojit na dané orientované přímce AB bod,jehož dělící poměr vůči bodům A, B je dané číslo λ.

1.7. KontrolnÍ otázky 101.7 Kontrolní otázky1.1 Popište, jak lze určit odchylku dvou rovin.1.2 Uved’te kritérium rovnoběžnosti přímky a roviny a kritérium rovnoběžnosti dvou rovin.1.3 Uved’te kritérium kolmosti přímky a roviny a kritérium kolmosti dvou rovin.1.4 Proč nemůže dělící poměr podle uvedené definice nabývat hodnoty 1?

Kapitola 2Nevlastní elementy2.1 Úvodní úvahaJe dána přímka q a bod P , který na této přímce neleží. Bodem P prochází přímka p (obr.2.1).Otáčíme přímkou p kolem bodu P a sestrojujeme průsečíky přímky p s přímkou q.Obrázek 2.1:V určitém okamžiku se přímka p dostane do speciální polohy (p ‖ q), kdy průsečík neexistuje.Nyní nastávají dvě možnosti: bud’ ve svých úvahách budeme uvádět tento případ zvlášt’, nebosi pomůžeme tím, že i pro tuto situaci zavedeme průsečík a budeme rovnoběžky považovat zapřímky, které mají společný bod. Tento průsečík, který ovšem nemůžeme zobrazit, nazvemenevlastním bodem.2.2 Nevlastní bod, přímka a rovinaDefinice 2.1 Všechny navzájem rovnoběžné přímky v prostoru mají společný právě jeden bod,který nazýváme nevlastním bodem. (Někdy říkáme, že rovnoběžné přímky mají stejný směr- nahradili jsme tedy pojem směr pojmem nevlastní bod.) - obr. 2.2Podobnou úvahu jako v obr. 2.1 můžeme provést pro dvě roviny a vyslovíme další definice:11

2.3. KontrolnÍ otázky 12Obrázek 2.2: Obrázek 2.3:Definice 2.2 Všechny navzájem rovnoběžné roviny v prostoru mají společnou právě jednupřímku, kterou nazýváme nevlastní přímkou - obr. 2.3.Definice 2.3Nevlastní rovina je množina všech nevlastních bodů a nevlastních přímek.Nevlastní útvary označujeme stejně jako vlastní, pouze připojujeme index ∞. Tedy např.A ∞ je nevlastní bod, p ∞ je nevlastní přímka apod.Euklidovský prostor obsahuje pouze vlastní útvary. Jestliže k němu přidáme právě zavedenénevlastní body, přímky a roviny, dostaneme nový prostor, který nazýváme projektivněrozšířený euklidovský prostor (nebo zkráceně rozšířený euklidovský prostor).V rozšířeném euklidovském prostoru platí pro vlastní útvary všechny axiomy a věty, kteréplatily v euklidovském prostoru. Pro nevlastní útvary musíme předpokládat platnost dalšíchtvrzení o incidenci vlastních a nevlastních útvarů:• Na každé vlastní přímce leží právě jeden nevlastní bod.• V každé vlastní rovině leží právě jedna nevlastní přímka.• Nevlastní body všech vlastních přímek jedné roviny leží na nevlastní přímce této roviny.Poznámka 2.1 Nevlastní bod na vlastní přímce značíme A ∞ a někdy připojujeme k příslušnépřímce šipku, což ale nesmí vést k domněnce, že na vlastní přímce existují dva různé nevlastníbody. Vlastní přímka má jediný nevlastní bod, nebot’ patří jednomu systému navzájem rovnoběžnýchpřímek. Dvě rovnoběžné přímky mají jeden společný nevlastní bod.2.3 Kontrolní otázky2.1 Definujte nevlastní bod přímky.2.2 Kolik nevlastních bodů leží na jedné přímce (rozlište přímku vlastní a nevlastní)?2.3 Je pravdivé tvrzení, že v rozšířené euklidovské rovině mají dvě různé přímky právě jedenspolečný bod? Je toto trvzení pravdivé i pro rozšířený euklidovský prostor?

Kapitola 3Kuželosečky3.1 ÚvodKuželosečka je rovinná křivka, kterou získáme jako průnik rotační kuželové plochy a roviny.Kuželosečky můžeme rozdělit na singulární, pokud rovina řezu prochází vrcholem rotačníkuželové plochy (bod, přímka, dvě přímky) a regulární, jestliže rovina řezu vrcholem neprochází(elipsa, hyperbola, parabola). V dalším textu nejprve uvedeme definice a tzv. ohniskové vlastnostikuželoseček, přičemž se nejvíce zaměříme na elipsu, protože elipsa je afinním obrazemkružnice, a tedy se s ní často setkáme v rovnoběžném promítání.Protože ohniska kuželoseček nejsou invariantem (nezobrazují se do ohnisek) afinních zobrazení,zaměříme se v další části na dvě věty, které nevyužívají ohniskových vlastností, ale pracujípouze s body, tečnami a incidencí.Poznámka 3.1 Sečna kuželosečky (resp. jiné křivky) je spojnice dvou bodů kuželosečky. Tečnulze definovat jako limitní případ sečny, pokud tyto dva body splynou.3.2 ElipsaDefinice 3.1 Elipsa je množina všech bodů, které mají od dvou daných vlastních bodů F, Gstálý součet vzdáleností 2a, větší než vzdálenost daných bodů (obr. 3.1).Body F, G se nazývají ohniska, spojnice bodů elipsy s ohnisky jsou průvodiče, středúsečky F G je střed elipsy. Přímka F, G je osou souměrnosti elipsy a nazýváme ji hlavní osa,stejným názvem označujeme i vzdálenost bodů A, B elipsy ležících na této ose, polovině tétovzdálenosti říkáme hlavní poloosa a značíme a. Osu úsečky F, G nazýváme vedlejší osa,stejným názvem označujeme i vzdálenost bodů C, D elipsy ležících na této ose, polovině tétovzdálenosti říkáme vedlejší poloosa a značíme b. Vzdálenost ohniska od středu elipsy senazývá lineární výstřednost neboli excentricita a značíme ji e. Pro poloosy a excentricituplatí vztaha 2 = b 2 + e 2.13

3.2. Elipsa 14Obrázek 3.1:3.2.1 Rovnice elipsyV této podkapitole používáme pojmový aparát z kapitoly Analytická geometrie (viz. ??), jemožné tuto část vynechat a vrátit se k ní později.Pokud umístíme elipsu tak, aby její osy ležely na souřadnicových osách (střed je v počátkusouřadnicové soustavy), potom ohniska mají souřadnice F = [−e, 0], G = [e, 0] a bod elipsyM = [x, y].Z definice elipsy platí, že |F M| + |GM| = 2a tj. √ (x + e) 2 + y 2 + √ (x − e) 2 + y 2 = 2a. Poúpravě získáme kanonickou rovnicix 2a + y22 b = 1. 2Jestliže umístíme střed elipsy do bodu S = [s 1 , s 2 ] (a osy zůstanou rovnoběžné se souřadnicovýmiosami), pak má elipsa rovnici(x − s 1 ) 2+ (y − s 2) 2= 1.a 2 b 2Parametrické vyjádření vyjádření lze odvodit z tzv. trojúhelníkové konstrukce elipsy (vizobr. 3.2). Jsou dány dvě soustředné kružnice se společným středem v bodě S = [0, 0] a poloměrya, b (a > b). Bodem S vedeme polopřímku r, která protíná kružnice v bodech A, B. BodemA vedeme rovnoběžku s osou y a bodem B rovnoběžku s osou x. Průsečík těchto rovnoběžekoznačíme X = [x, y] a odvodíme jeho souřadnice. Odvození ukážeme pro první kvadrant t ∈(0; π/2), v ostatních kvadrantech bude situace analogická.Souřadnice bodu A resp. B jsou [x a , y a ] = [a cos t, a sin t], resp. [x b , y b ] = [b cos t, b sin t].Z pravoúhlého trojúhelníku ABX lze vyjádřit velikosti odvěsen v = |AX| = (a − b) sin t,u = |BX| = (a − b) cos t. Souřadnice bodu X = [x, y] můžeme vyjádřit pomocí souřadnic bodůA, B a velikostí u, v:x = x b + u = b cos t + (a − b) cos t = a cos ty = y a − v = a sin t − (a − b) sin t = b sin t.Bod X je bodem elipsy, protože jeho souřadnice vyhovují kanonické rovnici uvedené výše ax = a cos t, b sin t, t ∈ (0; 2π)

3.2. Elipsa 15je parametrickým vyjádřením elipsy.Obrázek 3.2: Obrázek 3.3:3.2.2 Proužková konstrukce elipsyBodem X vedeme rovnoběžku q s polopřímkou r. Přímka q protne hlavní a vedlejší osu elipsyv bodech P a R. Protože r ‖ q, BX ‖ SP a AX ‖ SR, platí také, že |RX| = |SA| = a a|XP | = |SB| = b .Příklad 3.1 Elipsa je určena hlavní osou AB a bodem M, který je bodem elipsy. Určetevelikost vedlejší poloosy elipsy - obr. 3.4.Řešení: (obr. 3.5)1. Sestrojíme osu o úsečky AB.2. Sestrojíme kružnici f ≡ (M, a), velikost hlavní poloosy a je rovna polovině vzdálenostibodů A, B.3. Sestrojíme bod R jako průsečík kružnice f s osou o (ze dvou možností vybereme bod,který leží v opačné polorovině k polorovině určené osou AB a bodem M).4. Sestrojíme průsečík P úsečky RM s osou AB.5. Velikost b vedlejší poloosy je vzdálenost bodů P M.3.2.3 Oskulační kružnice elipsyPokud jsme nuceni sestrojit elipsu pomocí kružítka a pravítka, můžeme ji ve vrcholech nahraditoblouky tzv. oskulačních kružnic.Příklad 3.2 Sestrojte libovolný bod a oskulační kružnice elipsy určené hlavní a vedlejší osou- obr. 3.6.Řešení: (obr. 3.7)□

3.2. Elipsa 16Obrázek 3.4: Obrázek 3.5:1. Sestrojíme úsečku UW velikosti 2a = |AB| a zvolíme bod V na úsečce UW .2. Určíme ohniska F, G. Bod X je průsečíkem kružnic u 1 ≡ (F, |UV |) a u 2 ≡ (G, |V W |).3. Sestrojíme bodem C rovnoběžku s hlavní osou a bodem B rovnoběžku s vedlejší osou(tečny ve vrcholech).4. Průsečíkem rovnoběžek vedeme kolmici r k přímce CB.5. Průsečíky přímky r s hlavní a vedlejší osou jsou středy S 1 , S 2 oskulačních kružnic k 1 ≡(S 1 , |S 1 B|), k 2 ≡ (S 2 , |S 2 C|).□Obrázek 3.6: Obrázek 3.7:3.2.4 Rytzova konstrukcePrůměr elipsy je úsečka, která prochází středem elipsy a její krajní body leží na elipse. Narozdíl od kružnice není elipsa svým průměrem určena. Jednoznačně je určena tzv. sdruženýmiprůměry, pro které platí, že tečny v krajních bodech jednoho průměru jsou rovnoběžnés průměrem sdruženým.

3.2. Elipsa 17Obrázek 3.8:Příklad 3.3 Sestrojte hlavní a vedlejší osu elipsy určené sdruženými průměry - obr. 3.9.Řešení: (Rytzova konstrukce - obr. 3.10)1. K průměru KL vedeme bodem S kolmici u.2. Na kolmici sestrojíme bod Q tak, že na u naneseme od bodu S délku |QS| = |KS|. BodQ leží ve stejné polorovině určené hraniční přímkou KL jako bod M.3. Sestrojíme přímku QM.4. O je střed úsečky QM.5. Sestrojíme kružnici r ≡ (O, |OS|).6. QM ∩ r = {R, P }.7. Přímky RS a P S udávají polohu hlavní a vedlejší osy elipsy. Hlavní osa prochází ostrýmúhlem sdružených průměrů.8. Velikost hlavní osy elipsy a = |P M|. Velikost vedlejší osy elipsy b = |RM|.□Obrázek 3.9: Obrázek 3.10:3.2.5 Tečna a ohniskové vlastnosti elipsyTečna elipsy je přímka, která má s elipsou společný právě jeden bod. Při sestrojování obrysuněkterých těles (kužel) budeme hledat tečny z bodu (nebo v bodě) k elipse. Následující tři větyposkytují potřebný návod k těmto konstrukcím.

3.2. Elipsa 18Věta 3.1 Tečna elipsy půlí vnější úhly průvodičů dotykového bodu (viz obr. 3.1).Obrázek 3.11: Obrázek 3.12:Věta 3.2 Množina všech bodů, které jsou souměrně sdružené s jedním ohniskem elipsy podlejejích tečen, je kružnice se středem v druhém ohnisku o poloměru rovném velikosti hlavní osyelipsy.Tato kružnice se nazývá řídící kružnice (viz obr. 3.11).Věta 3.3 Množina všech pat kolmic, které jsou spuštěny z ohnisek elipsy na její tečny, jekružnice opsaná okolo středu elipsy poloměrem rovným velikosti hlavní poloosy.Tato kružnice se nazývá vrcholová kružnice (viz obr. 3.12).Příklad 3.4 Elipsa je určena hlavní a vedlejší osou. Z bodu M ved’te tečny k zadané elipse -obr. 3.13.Řešení: (pomocí vrcholové kružnice - obr. 3.14)1. Sestrojíme vrcholovou kružnici r ≡ (S, a).2. Sestrojíme Thaletovu kružnici k nad úsečkou GM.3. Sestrojíme průsečíky U 1 , U 2 kružnic k, r.4. Tečny t 1 resp. t 2 jsou určeny body U 1 M resp. U 2 M.5. Pokud chceme nalézt dotykový bod T , sestrojíme bod G ′ souměrně sdružený k ohniskuG podle tečny t 2 . Bod T je průsečíkem přímek F G ′ a t 2 . Druhý dotykový bod bychomnašli analogicky.Řešení: (pomocí řídící kružnice - obr. 3.15)1. Sestrojíme řídící kružnici d ≡ (F, 2a).2. Sestrojíme kružnici k ≡ (M, |MG|).3. Bod G ′ (bod souměrně sdružený k ohnisku podle tečny) je průsečík kružnic k, r.4. Tečna t 2 je kolmá k úsečce GG ′ . (Tečnu t 1 najdeme pomocí druhého průsečíku kružnick, r - konstrukce není v obrázku znázorněna.)5. Dotykový bod T je průsečíkem přímek F G ′ a t 2 .□□

3.3. Hyperbola 19Obrázek 3.13: Obrázek 3.14:Obrázek 3.15:3.3 HyperbolaDefinice 3.2 Hyperbola je množina všech bodů, které mají od dvou daných pevných bodů F, Gstálý rozdíl vzdáleností 2a, menší než vzdálenost daných bodů (obr. 3.16).Body F, G se nazývají ohniska, spojnice bodů hyperboly s ohnisky jsou průvodiče, středúsečky F G je střed hyperboly. Vzdálenost ohniska od středu elipsy se nazývá lineární výstřednostneboli excentricita a značíme ji e. Přímka F, G je osou souměrnosti hyperboly a nazývámeji hlavní osa, stejným názvem označujeme i vzdálenost bodů A, B hyperboly ležících na tétoose, polovině této vzdálenosti říkáme hlavní poloosa a značíme a. Osu úsečky F, G nazývámevedlejší osa, vedlejší poloosa nazýváme velikost b, pro kterou platí vztah.e 2 = a 2 + b 2

3.4. Parabola 20Obrázek 3.16:3.3.1 Tečna a ohniskové vlastnosti hyperbolyPro hyperbolu platí podobné věty jako pro elipsu a lze je využít při hledání tečny hyperboly.Pro tečny v nevlastních bodech používáme označení asymptoty.Věta 3.4 Tečna hyperboly půlí vnější úhly průvodičů dotykového bodu. (viz obr. 3.16).Věta 3.5 Množina všech bodů, které jsou souměrně sdružené s jedním ohniskem hyperbolypodle jejích tečen, je kružnice se středem v druhém ohnisku o poloměru rovném velikosti hlavníosy hyperboly.Tato kružnice se nazývá řídící kružnice (viz obr. 3.17).Věta 3.6 Věta 3: Množina všech pat kolmic, které jsou spuštěny z ohnisek hyperboly na jejítečny, je kružnice opsaná okolo středu hyperboly poloměrem rovným velikosti hlavní poloosy.Tato kružnice se nazývá vrcholová kružnice (viz obr. 3.18).3.4 ParabolaDefinice 3.3 Parabola je množina všech bodů, které mají od pevného bodu F a pevné přímkyd, která tímto bodem neprochází, stejné vzdálenosti (obr. 3.19).Bod F se nazývá ohnisko, přímka d řídící přímka, spojnice bodů paraboly s ohniskema kolmice daným bodem k řídící přímce jsou průvodiče. Přímka procházející ohniskem F akolmá na řídící přímku je osou souměrnosti paraboly a nazýváme ji osa paraboly. Průsečík Vosy s parabolou je vrchol paraboly. Vzdálenost ohniska od řídící přímky se nazývá parametra značí se p.Oskulační kružnice v hlavním vrcholu paraboly má střed S na ose paraboly ve vzdálenostip od vrcholu V (viz obr. 3.19).

3.4. Parabola 21Obrázek 3.17: Obrázek 3.18:Obrázek 3.19:3.4.1 Tečna a ohniskové vlastnosti parabolyPro parabolu platí podobné věty jako pro elipsu a hyperbolu, pouze místo řídící a vrcholovékružnice dostáváme řídící a vrcholovou přímku. Tyto věty lze opět využít při hledání tečnyparaboly.Věta 3.7 Tečna paraboly půlí vnější úhly průvodičů dotykového bodu (viz obr. 3.19).Věta 3.8 Množina všech bodů, které jsou souměrně sdružené s ohniskem paraboly podle jejíchtečen, je její řídící přímka. (viz obr. 3.20).Věta 3.9 Množina všech pat kolmic, které jsou spuštěny z ohniska na tečny paraboly, je vrcholovátečna paraboly. (viz obr. 3.21).

3.5. Pascalova a Brianchonova věta 22Obrázek 3.20: Obrázek 3.21:3.5 Pascalova a Brianchonova větaVěta 3.10 (Pascalova věta) Průsečíky tří dvojic protějších stran šestiúhelníka vepsaného dokuželosečky leží na jedné přímce tzv. Pascalově přímce (obr. 3.22).Obrázek 3.22:P = 12 ∩ 45Q = 23 ∩ 56R = 34 ∩ 61Příklad 3.5 Sestrojte další bod kuželosečky k(A, B, C, D, E) určené pěti body - obr. 3.23.Řešení: (volba přímky, na které leží hledaný bod - obr. 3.24)1. Očíslujeme body např. A = 1, B = 4, C = 2, D = 5, E = 3 a hledáme bod F = 6.2. Protože hledáme libovolný bod, můžeme přímku, na které budeme bod 6 hledat, vhodnězvolit. Volíme přímku procházející bodem 1 a označíme ji 16 (spojnice bodů 1 a 6)3. Sestrojíme bod P , který je průsečíkem spojnic 12 a 45.4. Sestrojíme bod R, který je průsečíkem spojnic 34 a 16.

3.5. Pascalova a Brianchonova věta 235. Sestrojíme Pascalovu přímku p = P R.6. Sestrojíme bod Q, který je průsečíkem Pascalovy přímky p a přímky 23.7. Sestrojíme přímku 56, která je spojnicí bodů Q a 5.8. Bod F = 6 je průsečíkem přímek 16 a 56.□Obrázek 3.23: Obrázek 3.24:Poznámka 3.2 Pokud dva body kuželosečky splynou, pak jejich spojnice přejde v tečnu (vizobr. 3.25). Pokud splynou dvě tečny, pak jejich průsečík přejde v dotykový bod (viz obr. 3.26).Techto úvah využijeme v následujících příkladech.Obrázek 3.25: Obrázek 3.26:Příklad 3.6 Kuželosečka k(A, B, C, D, E) je určena pěti body. Sestrojte tečnu k této kuželosečcev bodě A - obr. 3.27.Řešení: (obr. 3.28)

3.5. Pascalova a Brianchonova věta 241. Protože hledáme tečnu v bodě A, označíme tento bod jako dva body, které splynuly (a vPascalově větě je využívána jejich spojnice) A = 1 = 6.2. Očíslujeme ostatní body např. B = 2, C = 5, D = 3, E = 4 a hledáme spojnici 16.3. Sestrojíme bod P , který je průsečíkem spojnic 12 a 45.4. Sestrojíme bod Q, který je průsečíkem spojnic 23 a 56.5. Sestrojíme Pascalovu přímku p = P Q.6. Sestrojíme bod R jako průsečík Pascalovy přímky p a přímky 34.7. Sestrojíme přímku 16, která je spojnicí bodů R a 1 = 6.8. Přímka t A = 16 je tečnou kuželosečky v bodě 1 = 6.□Obrázek 3.27: Obrázek 3.28:Příklad 3.7 Kuželosečka k(A, B, b, D, E) je určena pěti body a tečnou v jednom z nich. Sestrojtetečnu k této kuželosečce v bodě A - obr. 3.29.Řešení: (obr. 3.30)1. Protože hledáme tečnu v bodě A, označíme tento bod jako dva body, které splynuly (a vPascalově větě je využívána jejich spojnice) A = 1 = 2.2. Protože přímka b je tečnou v bodě B, označíme i bod B jako dva body, které splynuly (av Pascalově větě je využívána jejich spojnice) B = 3 = 4 a přímku b jako spojnici 34.3. Očíslujeme ostatní body např. D = 5, E = 6 a hledáme spojnici 12.4. Sestrojíme bod Q, který je průsečíkem spojnic 23 a 56.5. Sestrojíme bod R, který je průsečíkem spojnic 34 a 16.6. Sestrojíme Pascalovu přímku p = QR.7. Sestrojíme bod P jako průsečík Pascalovy přímky p a přímky 45.8. Sestrojíme přímku 12, která je spojnicí bodů P a 1 = 2.9. Přímka t A = 12 je tečnou kuželosečky v bodě 1 = 2.□

3.5. Pascalova a Brianchonova věta 25Obrázek 3.29: Obrázek 3.30:Obrázek 3.31:p = (1 ∩ 2)(4 ∩ 5)q = (2 ∩ 3)(5 ∩ 6)r = (3 ∩ 4)(6 ∩ 1)Věta 3.11 (Brianchonova věta) Spojnice tří dvojic protějších vrcholů šestiúhelníka opsanéhokuželosečce procházejí jedním bodem tzv. Brianchonovým bodem (obr. 3.31).Příklad 3.8 Kuželosečka k(a, b, c, d, e) je určena pěti tečnami. Sestrojte další tečnu této kuželosečky- obr. 3.32.Řešení: (obr. 3.33)1. Očíslujeme přímky např. a = 1, b = 2, c = 3, d = 4, e = 5 a hledáme přímku f = 6.2. Protože hledáme libovolnou přímku, můžeme zvolit bod, kterým přímka bude procházet.Volíme bod na přímce 1 a označíme ho 16 (průsečík přímek 1 a 6)3. Sestrojíme přímku p, která je spojnicí průsečíků 12 a 45.4. Sestrojíme přímku r, která je spojnicí průsečíků 34 a 16.5. Sestrojíme Brianchonův bod B, který je průsečíkem přímek p a r.6. Sestrojíme přímku q, která je spojnicí Brianchonova bodu B a průsečíku 23.

3.6. KontrolnÍ otázky 267. Sestrojíme bod 56, který je průsečíkem přímek q a 5.8. Tečna f = 6 je spojnicí bodů 16 a 56.□Obrázek 3.32: Obrázek 3.33:Příklad 3.9 Kuželosečka k(a, b, c, d, D) je určena pěti tečnami a jedním bodem dotyku (bodD na tečně d). Sestrojte dotykový bod A na tečně a - obr. 3.34.Řešení: (obr. 3.35)1. Protože na tečně d známe dotykový bod, označíme ji jako dvě tečny, které splynulyd = 5 = 6 a dotykový bod jako jejich průsečík D = 56.2. Přímku a, na které hledáme dotykový bod, také označíme jako dvě přímky , které splynulya = 1 = 2 a hledáme jejich průsečík A = 12.3. Očíslujeme ostatní přímky např. b = 3, c = 4.4. Sestrojíme přímku q, která je spojnicí průsečíků 23 a 56.5. Sestrojíme přímku r, která je spojnicí průsečíků 34 a 16.6. Sestrojíme Brianchonův bod B, který je průsečíkem přímek q a r.7. Sestrojíme přímku p, která je spojnicí Brianchonova bodu B a průsečíku 45.8. Sestrojíme bod 12, který je průsečíkem přímek p a 1 = 2.9. Bod 12 je dotykovým bodem na tečně a.3.6 Kontrolní otázky3.1 Kolika obecnými body je kuželosečka jednoznačně určena.3.2 Co jsou to sdružené průměry elipsy? Které průměry kružnice můžeme považovat zasdružené pokud bychom uvažovali kružnici jako speciální případ elipsy (ohniska splynou)?3.3 Kolik nevlastních bodů mají jednotlivé regulární kuželosečky?□

3.6. KontrolnÍ otázky 27Obrázek 3.34: Obrázek 3.35:

Kapitola 4Elementární plochy a tělesa4.1 Základní pojmyElementárními plochami budeme rozumět jehlanovou, hranolovou, kuželovou, válcovou a kulovouplochu a elementárními tělesy jehlan, hranol, kužel, válec a kouli. Elementární tělesaznáte z předchozího studia na střední škole. Zde je jen dáme do souvislostí s nově definovanýmipojmy.4.1.1 Jehlanová plocha, jehlanJehlanová plocha je určena rovinnou lomenou čárou - polygonem c (c ⊂ σ) a bodem V , kterýneleží v rovině polygonu (V ∉ σ), a je tvořena přímkami, které protínají polygon c a procházejíbodem V - obr. 4.1 a).Je-li polygon uzavřený, pak množina přímek, které procházejí daným bodem V a protínajívnitřek polygonu nebo polygon, se nazývá jehlanový prostor. Přímky určené vrcholem V avrcholy polygonu jsou hrany jehlanové plochy.Rovina, která prochází vrcholem, se nazývá vrcholová rovina.Jehlan je průnik jehlanového prostoru a prostorové vrstvy určené rovinou σ řídícího polygonua vrcholové roviny σ ′ ‖ σ - obr. 4.1 c). ) Výška jehlanu je vzdálenost vrcholu V od rovinypodstavy. Má-li podstava střed S a leží-li vrchol V na kolmici vztyčené v bodě S k roviněpodstavy, nazýváme jehlan kolmý a SV je jeho osa. V opačném případě je jehlan kosý.4.1.2 Hranolová plocha, hranolHranolová plocha je určena rovinnou lomenou čárou - polygonem c (c ⊂ σ) a směrem s, kterýnenáleží dané rovině (s ̸‖ σ), a je tvořena přímkami, které protínají polygon c a jsou směru s -obr. 4.1b).Je-li polygon uzavřený, pak množina přímek směru s, které protínají polygon nebo vnitřekpolygonu, se nazývá hranolový prostor. Přímky určené vrcholy polygonu a směru s jsou hranyhranolové plochy. V projektivním rozšíření euklidovského prostoru lze definovat hranolovouplochu jako speciální případ jehlanové plochy, jejímž vrcholem je nevlastní bod. Vrcholovourovinou je každá rovina směru s.28

4.1. ZákladnÍ pojmy 29Hranol je průnik hranolového prostoru a prostorové vrstvy určené rovinou σ řídícího polygonua roviny σ ′ ‖ σ - obr. 4.1d). Výška hranolu je vzdálenost rovin podstav. Jsou-li pobočnéhrany kolmé na roviny podstav, nazýváme hranol kolmý a spojnice středů podstav je jeho osou(pokud existuje). V opačném případě je hranol kosý. Hranol, jehož podstavou je rovnoběžník,nazýváme rovnoběžnostěn.Obrázek 4.1: Obrázek 4.2:4.1.3 Kuželová plocha, kuželKuželová plocha je určena rovinnou křivku k (k ⊂ σ) a bodem V , který neleží v rovině danékřivky (V ∉ σ), a je tvořena přímkami, které protínají křivku k a procházejí bodem V - obr.4.2 a).Je-li křivka k uzavřená, pak množina přímek, které procházejí daným bodem V a protínajíkřivku nebo vnitřek křivky, se nazývá kuželový prostor. Přímka určená vrcholem V a bodemkřivky k je površka kuželové plochy.Rovina, která prochází vrcholem, se nazývá vrcholová rovina.Kužel je průnik kuželového prostoru a prostorové vrstvy určené rovinou σ řídícího polygonua vrcholové roviny σ ′ ‖ σ - obr. 4.2 c).Je-li řídící křivkou kuželové plochy kružnice (řídící kružnice), kuželová plocha se nazývákruhová. Jestliže je spojnice středu S řídící kružnice k a vrcholu V kolmá na rovinu σ, paknazýváme kuželovou plochu kolmou nebo rotační a přímku SV osou kuželové plochy. Rotačníkuželovou plochu můžeme také získat rotací přímky, která protíná osu otáčení a není k ní kolmá.Není-li přímka SV kolmá na rovinu řídící kružnice, nazývá se kuželová plocha kosá. Podobněkolmý nebo rotační kužel má osu kolmou k rovině podstavy na rozdíl od kosého kužele.

4.2. KontrolnÍ otázky 304.1.4 Válcová plocha, válecVálcová plocha je určena rovinnou křivkou k (k ⊂ σ) a směrem s, který nenáleží dané rovině(s ̸‖ σ), a je tvořena přímkami, které protínají křivku k a jsou směru s - obr. 4.2 b).Je-li křivka k uzavřená, pak množina přímek směru s, které protínají křivku nebo procházejívnitřním bodem křivky, se nazývá válcový prostor. Přímka určená bodem křivky k a směrus je površka. Podobně jako u hranolové plochy, můžeme v projektivním rozšíření euklidovskéhoprostoru definovat válcovou plochu jako speciální případ kuželové plochy, jejímž vrcholem jenevlastní bod. Vrcholovou rovinou je každá rovina směru s.Válec je průnik válcového prostoru a prostorové vrstvy určené rovinou σ řídícího polygonua roviny σ ′ ‖ σ - obr. 4.2 d).Je-li řídící křivkou válcové plochy regulární kuželosečka, získáme eliptickou, parabolickouči hyperbolickou válcovou plochu. Jestliže je řídící křivkou kružnice, nazývá se válcová plochakruhová. Jestliže jsou površky kolmé na rovinu řídící kružnice, dostáváme kolmou kruhovouneboli rotační válcovou plochu, v opačném případě je plocha kosá.Poznámka 4.1 Každá křivka (podle naší definice rovinná) na válcové nebo kuželové plošemůže být řídící křivkou této plochy. Řezem rotační kuželové plochy rovinou může být, podlepolohy roviny řezu, i jiná kuželosečka. To znamená, že zvolíme-li tuto kuželosečku jako řídícíkřivku, dostaneme opět rotační kuželovou plochu. Nemá tedy smysl, na rozdíl od válcovýchploch, rozlišovat hyperbolickou nebo parabolickou kuželovou plochu od eliptické kuželové plochy.4.1.5 Kulová plocha, kouleKulová plocha je množina všech bodů, které mají od daného bodu S vzdálenost rovnudanému kladnému číslu r. Koulí rozumíme množinu všech bodů, které mají od daného boduS vzdálenost menší nebo rovnu danému kladnému číslu r.4.2 Kontrolní otázky4.1 Popište a načrtněte pravidelný trojboký jehlan a pravidelný čtyřboký hranol.4.2 Definujte kosý kruhový válec.4.3 Vysvětlete rozdíl mezi koulí a kulovou plochou.

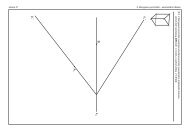
Kapitola 5Základy promítání5.1 ÚvodDeskriptivní geometrie se zabývá studiem takových zobrazení, kterými můžeme zobrazit prostorovéútvary do roviny a naopak. Zpravidla požadujeme, aby tato zobrazení byla vzájemnějednoznačná. Vzájemně jednoznačným zobrazením v deskriptivní geometrii říkáme zobrazovacímetody.Protože deskriptivní geometrie vznikla z potřeb praxe, je důležité, aby bylo možné snadnovyčíst velikost objektů, jejich tvar a vzájemnou polohu jednotlivých částí. Další požadavky setýkají názornosti a snadného řešení stereometrických úloh.Procesu našeho vidění se nejvíce blíží středové promítání a jeho speciální případ lineárníperspektiva. Tyto zobrazovací metody jsou velmi názorné a často se s nimi setkáváme v situacích,kdy je třeba reálné zobrazení světa, například v umění nebo architektuře. Nevýhodoustředového promítání je složitost konstrukcí a obtíže s měřením délek. Proto se v technicképraxi více používají zobrazovací metody, které můžeme označit společným názvem rovnoběžnápromítání. V následujícím textu se tedy velmi krátce zmíníme o principech středového promítání,ale podrobněji se budeme zabývat promítáním rovnoběžným a jeho speciálním případem -pravoúhlým promítáním.5.2 Středové promítáníZvolme v prostoru rovinu π, na kterou budeme zobrazovat - budeme jí říkat průmětna a bodS (vlastní), který neleží v rovině π. Bod S se nazývá střed promítání. Libovolný bod Av prostoru (různý od bodu S) zobrazíme do roviny π následujícím způsobem: Body S a Aproložíme přímku p. Přímka p se nazývá promítací přímka. Průsečík A ′ přímky p s rovinou πje středovým průmětem bodu A do roviny π. Podobně sestrojíme bod B ′ jako středový průmětbodu B - obr. 5.1.Vlastnosti středového promítání1. Středovým průmětem bodu různého od středu promítání je bod. (Bod S ve středovémpromítání nemůžeme zobrazit.)31

5.3. Rovnoběžné promÍtánÍ 322. Středovým průmětem přímky, která neprochází středem promítání S, je přímka. Středovýmprůmětem přímky procházející středem promítání S je bod.3. Středovým průmětem roviny procházející středem promítání S je přímka. Středovýmprůmětem roviny, která neprochází středem promítání S, je celá průmětna.4. Středovým průmětem bodu A ležícího na přímce k je bod A ′ ležící na středovém průmětuk ′ přímky k. Obecně leží-li bod na nějaké čáře, pak jeho průmět leží na průmětu té čáry.Říkáme, že se zachovává incidence.Poznámka 5.1 Pokud budeme pracovat s body z projektivního rozšíření prostoru, zjistíme,že ve středovém promítání může být obrazem vlastního bodu bod nevlastní a naopak obrazemnevlastního bodu bod vlastní. Načrtněte si takovou situaci a uved’te vhodný reálný příklad(např. zobrazení železničních kolejí).Obrázek 5.1: Obrázek 5.2:5.3 Rovnoběžné promítáníPodobně jako ve středovém promítání zvolíme v rovnoběžném promítání rovinu π, na kteroubudeme zobrazovat, a které říkáme průmětna. Dále zvolíme přímku s, která není rovnoběžnás rovinou π. Říkáme, že přímka s nám určuje směr promítání. Rovnoběžný průmět A′ boduA získáme tak, že bodem A vedeme přímku p (nazýváme ji opět promítací přímka), která jerovnoběžná s přímkou s a najdeme její průsečík s rovinou π. Podobně najdeme průmět boduB - obr. 5.2.Pokud použijeme pojmy z kapitoly o nevlastních elementech, můžeme říct, že rovnoběžnépromítání je speciální případ středového promítání, kde středem promítání je nevlastní bod.Vlastnosti rovnoběžného promítání1. Rovnoběžným průmětem (vlastního) bodu je (vlastní) bod.

5.4. Pravoúhlé promÍtánÍ 332. Rovnoběžným průmětem přímky, která není směru promítání, je přímka. Rovnoběžnýmprůmětem přímky, která je směru promítání, je bod.3. Rovnoběžným průmětem roviny, která je směru promítání, je přímka. Rovnoběžnýmprůmětem roviny, která není směru promítání, je celá průmětna.4. Rovnoběžným průmětem bodu A ležícího na přímce k je bod A ′ ležící na rovnoběžnémprůmětu k ′ přímky k. Obecně leží-li bod na nějaké čáře, pak jeho průmět leží na průmětuté čáry.5. Rovnoběžným průmětem různoběžek a, b jsou různoběžné přímky nebo přímky splývající,pokud a, b nejsou směru promítání. Jestliže je jedna z přímek a, b směru promítání, pakrovnoběžným průmětem různoběžek a, b je přímka a na ní bod.6. Rovnoběžnost se zachovává, tj. rovnoběžné přímky se zobrazí na rovnoběžné nebo splývajícípřímky (nebo na dva body), rovnoběžné úsečky na rovnoběžné úsečky apod.7. Rovnoběžným průmětem rovnoběžných a shodných úseček jsou rovnoběžné a shodnéúsečky (popř. dva body).8. Rovnoběžným průmětem útvaru ležícího v rovině rovnoběžné s průmětnou je útvar s nímshodný.9. Dělící poměr se v rovnoběžném promítání zachovává, tj. například střed úsečky se zobrazína střed úsečky.Druhy rovnoběžného promítáníPodle vztahu směru promítání vzhledem k průmětně rozlišujeme dva druhy rovnoběžnéhopromítání. Jestliže směr promítání je kolmý k průmětně, pak hovoříme o pravoúhlém (nebotaké o kolmém či ortogonálním) promítání. Pokud směr promítání není kolmý k průmětně,mluvíme o kosoúhlém promítání. Připomeňme, že jsme vyloučili případ, kdy směr promítáníje rovnoběžný s průmětnou.5.4 Pravoúhlé promítáníVlastnosti, které jsme uvedli pro rovnoběžné promítání, doplníme dvěma větami, které platíjen pro pravoúhlé promítání.Věta 5.1 (Věta o pravoúhlém průmětu pravého úhlu) Pravoúhlým průmětem pravéhoúhlu je pravý úhel, jestliže alespoň jedno jeho rameno je rovnoběžné s průmětnou a druhé nenína průmětnu kolmé.Věta 5.2 Velikost pravoúhlého průmětu A ′ B ′ úsečky AB je menší nebo rovna velikosti úsečkyAB, tj. |A ′ B ′ | ≤ |AB|.5.5 Středová kolineaceJsou dány dvě různé roviny α a α ′ a bod S, který neleží v žádné z rovin α a α ′ . Středovákolineace je geometrická příbuznost, kdy bodu jedné roviny odpovídá jeho středový průmětz bodu S do druhé roviny. Průsečnice o rovin α a α ′ se nazývá osa kolineace (obr. 5.3).

5.5. Středová kolineace 34Obrázek 5.3: Obrázek 5.4:Vlastnosti středové kolineaceUvedeme vlastnosti středové kolineace, které vyplývají z vlastností středového promítání.1. Bodu odpovídá bod a přímce přímka.2. Přímky, které si odpovídají ve středové kolineaci, se protínají na ose kolineace nebo jsous ní rovnoběžné, což ale znamená, že mají společné nevlastní body.3. Body osy kolineace jsou samodružné, tj. vzor a obraz splývají.4. Středová kolineace zachovává incidenci. To znamená, že jestliže bod A leží na přímce b,pak pro jejich obrazy A ′ , b ′ opět platí A ′ ∈ b ′ .5. Body, které si odpovídají ve středové kolineaci, leží na přímce procházející středem kolineace.Poznámka 5.2 Je nutné si uvědomit, že středová kolineace obecně nezachovává rovnoběžnosta že vlastnímu bodu může odpovídat bod nevlastní a naopak. Také dělící poměr tří kolineárníchbodů se obecně ve středové kolineaci nezachovává.Středová kolineace v roviněProtože se zabýváme zobrazováním trojrozměrného prostoru na rovinu, zajímá nás, co se stane,promítneme-li středovou kolineaci do roviny.Promítneme rovnoběžně obě roviny α, α ′ a střed promítání S do průmětny π tak, aby směrpromítání nebyl rovnoběžný s žádnou z rovin α a α ′ (tj. žádná z rovin se nezobrazí jako přímka).Odpovídající si body A a A ′ promítnuté do π leží opět na přímce procházející průmětem středukolineace. Takto získanou příbuznost v rovině nazveme středovou kolineací v rovině - obr.5.4.Vlastnosti, které jsme uvedli pro středovou kolineaci mezi rovinami, platí také pro středovoukolineaci v rovině.Znalost středové kolineace využijeme např. při sestrojování řezů na jehlanu a kuželi.

5.5. Středová kolineace 35Středová kolineace v rovině je určena středem S, osou o a párem odpovídajících si bodů A,A ′ (body A, A ′ , S leží na jedné přímce). Pro sestrojování obrazů bodů ve středové kolineacijsou nejdůležitější tyto tři vlastnosti:1. Středová kolineace zachovává incidenci.2. Přímky, které si odpovídají ve středové kolineaci, se protínají na ose kolineace nebo jsous ní rovnoběžné.3. Body, které si odpovídají, leží na přímce procházející středem kolineace.Příklad 5.1 Středová kolineace v rovině je určena středem S, osou o a párem odpovídajícíchsi bodů A, A ′ - obr. 5.5. Sestrojíme obraz bodu B v kolineaci.Řešení: (obr. 5.6)1. Spojíme bod B se vzorem bodu, pro který známe jeho obraz, tj. v našem případě s bodemA - dostaneme přímku p.2. Najdeme obraz p ′ přímky p (p a p ′ se protínají na ose a přímka p ′ prochází bodem A ′ -vlastnost 2. a 1.)3. Protože body, které si odpovídají, leží na přímce procházející středem kolineace- vlastnost3., sestrojíme přímku SB.4. Bod B ′ leží v průsečíku přímek SB a p ′ .Obrázek 5.5: Obrázek 5.6:□Jak jsme již uvedli, obrazem vlastního bodu ve středové kolineaci nemusí vždy být vlastníbod. Stejně tak se některé nevlastní body zobrazí na vlastní body. Vzory a obrazy nevlastníchbodů nazýváme úběžníky. Vzor nevlastní přímky se nazývá úběžnice vzorů a obraz nevlastnípřímky se nazývá úběžnice obrazů.Nevlastní přímka má s osou o společný nevlastní bod (nevlastní bod osy o). Přímky, které siodpovídají v kolineaci se protínají na ose, pokud je tento bod nevlastní, pak jsou odpovídajícísi přímky rovnoběžné. Tedy obě úběžnice jsou rovnoběžné s osou kolineace.

5.5. Středová kolineace 36Příklad 5.2 Středová kolineace v rovině je určena středem S, osou o a párem odpovídajícíchsi bodů A, A ′ - obr. 5.7. Sestrojíme úběžnici obrazů.Řešení: (obr. 5.8)1. Zvolíme libovolný bod V ∞ na nevlastní přímce.2. Najdeme obraz V ′ nevlastního bodu V ∞ (bod V ′ je vlastní).3. Bod V ′ leží na úběžnici obrazů v ′ a ta je rovnoběžná s osou o.4. Podobně lze sestrojit úběžnici vzorů. Úběžnice vzorů je rovnoběžná s osou o a procházívzorem bodu U ∞ ′ (bod U ∞ ′ je libovolný bod nevlastní přímky).Obrázek 5.7: Obrázek 5.8:Příklad 5.3 Středová kolineace v rovině je určena středem S, osou o a párem odpovídajícíchsi přímek p, p ′ - obr. 5.9. Sestrojíme obě úběžnice.Řešení: (obr. 5.10)1. Označíme V ∞ nevlastní bod přímky p.2. Najdeme obraz V ′ nevlastního bodu V ∞ (V ′ ∈ p ′ ) a sestrojíme úběžnici obrazů v ′ (v ′ ‖o, V ′ ∈ v ′ ).3. Dále označíme bod U ′ ∞ nevlastní bod přímky p ′ .4. Najdeme vzor U nevlastního bodu U ′ ∞ (U ∈ p) a sestrojíme úběžnici vzorů v (v ‖ o, U ∈u).□Ve středové kolineaci v rovině je vzdálenost středu od jedné úběžnice rovna vzdálenostidruhé úběžnice od osy kolineace. Podíváme-li se znovu na obrázek 5.10, pak toto tvrzení plynez rovnoběžníka SUMV ′ .Středová kolineace v rovině se nazývá involutorní, když pro všechny body X, Y platí:jestliže X = Y ′ , pak Y = X ′ . V involutorní kolineaci úběžnice splývají a půlí vzdálenost středukolineace od osy.Necht’ body A, A ′ si odpovídají ve středové kolineaci, bod Ā je průsečík přímky AA′ s osou′ (A′ AĀ)o. Pak dvojpoměr (A AĀS) = je konstantní pro všechny páry odpovídajících si bodů.(A ′ AS)′Číslo k = (A AĀS) se nazývá charakteristika středové kolineace, charakteristika involutorníkolineace je k = −1.□

5.6. Osová afinita 37Obrázek 5.9: Obrázek 5.10:5.6 Osová afinitaJsou dány dvě různé roviny α a α ′ a směr s, který není rovnoběžný s žádnou z rovin α a α ′ .Osová afinita je geometrická příbuznost, kdy bodu jedné roviny odpovídá jeho rovnoběžnýprůmět ve směru s do druhé roviny.Průsečnice rovin α a α ′ se nazývá osa afinity (obr. 5.11).Obrázek 5.11: Obrázek 5.12:Vlastnosti osové afinity(vyplývají z rovnoběžného promítání)Vlastnosti 1.- 5. jsou podobné vlastnostem pro kolineaci, ale všimněte si pozorně vlastností6. a 7.1. Bodu odpovídá bod a přímce přímka.2. Přímky, které si odpovídají v osové afinitě, se protínají na ose afinity nebo jsou s nírovnoběžné.

5.6. Osová afinita 383. Body osy afinity jsou samodružné.4. Osová afinita zachovává incidenci.(To znamená, že jestliže bod A leží na přímce b, pakpro jejich průměty A ′ , b ′ opět platí A ′ ∈ b ′ .)5. Body, které si odpovídají v osové afinitě leží na rovnoběžce se středem promítání.6. Osová afinita zachovává rovnoběžnost.7. Osová afinita zachovává dělící poměr.Osová afinita v roviněPodobně jako kolineaci promítneme rovnoběžně i afinitu.Promítneme rovnoběžně obě roviny α, α ′ a směr promítání s do průmětny π tak, aby směrpromítání u do roviny π nebyl rovnoběžný s žádnou z rovin α a α ′ (tj. žádná z rovin se nezobrazíjako přímka) a aby nebyl rovnoběžný se směrem s (dostali bychom identitu). Odpovídající sibody A a A ′ promítnuté do π leží na přímce rovnoběžné s promítnutým směrem s.Takto získanou příbuznost nazveme osovou afinitou v rovině - obr. 5.12.Uvedené vlastnosti osové afinity mezi rovinami budou platit i pro osovou afinitu v rovině.Osovou afinitu využijeme při sestrojování řezů na hranolu a kuželi a při otáčení v Mongeověprojekci a axonometrii.Nejčastější určení osové afinity je osou o a párem odpovídajících si bodů A a A ′ (tím jeurčen směr afinity). Opět zopakujeme tři vlastnosti, které využijeme při sestrojování obrazunebo vzoru daného bodu:1. Osová afinita zachovává incidenci2. Přímky, které si odpovídají v osové afinitě, se protínají na ose afinity nebo jsou s nírovnoběžné.3. Body, které si odpovídají, leží na rovnoběžce se směrem afinity.Příklad 5.4 Osová afinita v rovině je určena osou o a párem odpovídajících si bodů A, A ′ -obr. 5.13. Sestrojíme obraz bodu B v afinitě.Řešení: (obr. 5.14)1. Spojíme bod B s bodem A - dostaneme přímku p. (Obecně se vzorem bodu, pro kterýznáme jeho obraz.)2. Najdeme obraz p ′ přímky p (p a p ′ se protínají na ose a přímka p ′ prochází bodem A ′ -vlastnost 2 a 1)3. Protože body, které si odpovídají, leží na přímce směru afinity a tento směr určuje přímkaAA ′ (vlastnost 3), sestrojíme přímku k rovnoběžnou s přímkou AA ′ a procházející bodemB.4. Bod B ′ leží v průsečíku přímek k a p ′ .□

5.7. Kružnice v osové afinitě a středové kolineaci 39Obrázek 5.13: Obrázek 5.14:Poznámka 5.3 Osová afinita může být určena i jiným způsobem než osou a párem odpovídajícíchbodů, např. osou, směrem a párem odpovídajících si přímek (které se protínajína ose) nebo dvěma páry odpovídajících si přímek. Stejně i kolineace může být určena jinaknež středem, osou a párem odpovídajících si bodů.Osovou afinitu můžeme chápat jako speciální případ středové kolineace, kdy střed kolineaceje nevlastním bodem. Vztah mezi afinitou a kolineací nám přiblíží schéma na obrázku 5.16.5.7 Kružnice v osové afinitě a středové kolineaciVe středové kolineaci odpovídá kuželosečce k kuželosečka k ′ (nemusí být stejného typu) a platí:1. Bodům a tečnám vzoru odpovídají body a tečny obrazu,2. Středu kuželosečky k obecně neodpovídá střed kuželosečky k ′ ,3. Průměru kuželosečky k obecně neodpovídá průměr kuželosečky k ′ ,4. Sdruženým průměrům kuželosečky k neodpovídají sdružené průměry kuželosečky k ′ .Jestliže kružnice k nemá s úběžnicí u žádný společný bod, pak se všechny její body zobrazína body vlastní a obrazem kružnice k ve středové kolineaci je elipsa; jestliže se kružnice kdotýká úběžnice u, pak se tento dotykový bod zobrazí na nevlastní bod a obrazem kružnice kve středové kolineaci je parabola; jestliže kružnice k úběžnici u protíná, pak obrazem kružnicek ve středové kolineaci je hyperbola, která má dva nevlastní body (viz obr. 5.15).V osové afinitě se všechny vlastní body zobrazí opět na vlastní body, kuželosečce k odpovídákuželosečka k ′ , je stejného typu a platí:1. Bodům a tečnám vzoru odpovídají body a tečny obrazu,2. Středu kuželosečky k odpovídá střed kuželosečky k ′ ,3. Průměru kuželosečky k odpovídá průměr kuželosečky k ′ ,

5.8. KontrolnÍ otázky 40Obrázek 5.15:4. Sdruženým průměrům kuželosečky k odpovídají sdružené průměry kuželosečky k ′ .Obrazem kružnice k v osové afinitě je tedy elipsa.5.8 Kontrolní otázky5.1 Vyslovte větu o pravoúhlém průmětu pravého úhlu.5.2 Jakou délku může mít (v porovnání s délkou zobrazované úsečky) průmět úsečky vpravoúhlém promítání a jakou v kosoúhlém?5.3 Rovnoběžné promítání zachovává dělící poměr. Je pravda, že obrazem středu úsečky jev rovnoběžném promítání střed úsečky, která je průmětem dané úsečky?5.4 Jakou vlastnost mají body, které leží na ose afinity nebo kolineace?5.5 Jakou vlastnost mají body úběžnic kolineace?

5.8. KontrolnÍ otázky 41Obrázek 5.16:

Kapitola 6Mongeovo promítání6.1 ÚvodMongeovo promítání je pravoúhlé promítání na dvě navzájem kolmé průmětny. Jeho výhodou jesnadné řešení stereometrických úloh, nevýhodou může být menší názornost a složitější orientaceve dvou pohledech na jeden objekt.Obrázek 6.1:Zvolíme v prostoru dvě navzájem kolmé roviny.Rovinu π volíme ve vodorovné poloze- říkáme jí půdorysna - a rovinu ν v polozesvislé - nárysna. Průsečnici rovin π a νztotožníme s osou x souřadnicového systému aříkáme jí základnice. Osu y volíme v roviněπ, tak aby byla kolmá k x. Průsečíkem O os xa y prochází osa z, leží v rovině ν a je kolmák osám x, y. V Mongeově promítání budemepři vynášení souřadnic používat zpravidla levotočivýsouřadnicový systém – viz obr. 6.2. Připoužití pravotočivého souřadnicového systémuby se kladné souřadnice x nanášely vlevo.Poznámka 6.1 Pokud bychom chtěli promítat pouze na jednu průmětnu, pak útvar, kterýpromítneme, nebude v prostoru jednoznačně určen. Další možností je použít kótované promítání,to znamená, že ke každému bodu budeme připisovat jeho vzdálenost od průmětny. Toto promítáníse používá při řešení střech a při tvorbě map (vstevnice), to znamená většinou v případech,kdy není nutné řešit složitější prostorové vztahy.6.2 Obraz boduNejprve kolmo promítneme bod B do půdorysny a průmět označíme indexem 1 - dostaneme bodB 1 - obr. 6.2a), potom bod B promítneme do nárysny, průmět označíme indexem 2 a získáme42

6.3. Obraz přÍmky 43bod B 2 - obr. 6.2b). Nyní máme dvě možnosti, jak si představit sdružení průmětů. Bud’ otočímerovinu π kolem osy x tak, aby kladná část osy y splynula se zápornou částí osy z - obr. 6.1nebo si představíme nárysnu a půdorysnu jako dvě průhledné folie, které položíme na sebe, takaby se překrývaly průměty osy x 1 a x 2 a bod O 1 a O 2 - obr. 6.2.Bod B 1 nazýváme půdorysem a bod B 2 nárysem bodu B. Spojnice nárysu a půdorysutéhož bodu je kolmá k základnici a nazývá se ordinála. (Půdorys je vlastně pohled shora anárys je pohled zpředu).Z obrázku 6.2 c) je vidět, jak sestrojíme nárys a půdorys bodu, známe-li jeho souřadnice.V našem případě jsou všechny tři souřadnice kladné. Nárysu a půdorysu bodu B říkámesdružené průměty bodu B. (Neplést si se sdruženými průměry, ty najdeme u elipsy.)Obrázek 6.2:Příklad 6.1 Určeme, kde bude ležet nárys a půdorys bodů B, C, D, E, jestliže umístíme každýdo jiného kvadrantu vymezeného nárysnou a půdorysnou - obr. 6.3.Řešení: (obr. 6.4) Bod B, který se nachází nad půdorysnou a před nárysnou, má půdorys podosou a nárys nad osou x 1,2 .Bod C leží za nárysnou a nad půdorysnou a oba jeho průměty leží nad osou x 1,2 .Nárys i půdorys bodu E ležícího pod půdorysnou a před nárysnou najdeme pod osou x 1,2 .Pro bod D, který je za nárysnou a pod půdorysnou platí, že nárys je pod a půdorys nadosou x 1,2 .□6.3 Obraz přímkyZ vlastností rovnoběžného promítání víme, že obrazem přímky je bud’ přímka, nebo bod. Pokudpřímka p není kolmá k ose x, pak jejím půdorysem a nárysem jsou přímky p 1 a p 2 , které nejsoukolmé k ose x 1,2 - obr. 6.5 a 6.6. Jestliže je přímka kolmá k půdorysně je jejím půdorysembod a nárysem přímka kolmá k ose x 1,2 , pro přímku kolmou k nárysně bude nárysem boda půdorysem přímka kolmá k ose x 1,2 . Ve všech těchto případech je přímka svými průmětyjednoznačně určena.

6.3. Obraz přÍmky 44Obrázek 6.3: Obrázek 6.4:Je-li přímka kolmá k ose x a přitom není kolmá k žádné průmětně, pak její sdružené průmětysplývají a jsou kolmé k x 1,2 . Jen v tomto případě není přímka určena svými sdruženými průměty.K určení je v tomto případě nutná znalost např. průmětů dvou různých bodů přímky.Přímkou, která není kolmá k průmětně, můžeme proložit rovinu kolmou k průmětně. Tétorovině říkáme promítací rovina přímky. Přímkou můžeme proložit půdorysně promítacírovinu kolmou k půdorysně nebo nárysně promítací rovinu kolmou k nárysně.Na zvláštní polohy přímky vzhledem k průmětně se podívejme v příkladu 6.2.Obrázek 6.5: Obrázek 6.6:Příklad 6.2 V obrázku 6.7 určíme polohu jednotlivých přímek vzhledem k průmětnám.Řešení: Přímky p, q, r jsou kolmé k základnici. Přímka p je navíc kolmá k půdorysně a qje kolmá k nárysně. Přímka r není svými průměty jednoznačně určena a musíme ji dourčitsdruženými průměty dvou bodů, které na ní leží. Přímka s je rovnoběžná s půdorysnou a přímkat s nárysnou, s ′ v půdorysně leží a u je rovnoběžná se základnicí.□

6.4. Obraz roviny 45Obrázek 6.7:Vzájemný vztah přímky a bodu, který na ní leží, je v Mongeově promítání dán větou:Věta 6.1 Leží-li bod M na přímce p, pak M 1 ∈ p 1 a M 2 ∈ p 2 .Jestliže přímka p je určena svými průměty (tím vylučujeme přímky kolmé k ose x a nejsoupromítací), pak pro sdružené průměty bodu M a přímky p platí: pokud M 1 ∈ p 1 a M 2 ∈ p 2 , pakbod M leží na přímce p.Přímka je jednoznačně určena dvěma body. Pro sdružené průměty přímky můžeme vyslovitnásledující větu:Věta 6.2 Sdružené průměty přímky p = AB jsou v Mongeově promítání jednoznačně určenyprůměty dvou jejích bodů A, B.Vlastní bod, ve kterém přímka protne průmětnu, nazýváme stopník. Půdorysný stopníkP je bod, ve kterém přímka protne půdorysnu, nárysný stopník N je bod, ve kterém přímkaprotíná nárysnu - obr. 6.5.Pro půdorysný stopník P přímky p platí: P 1 ∈ p 1 , P 2 ∈ p 2 a P 2 ∈ x 1,2 .Pro nárysný stopník N přímky p platí: N 1 ∈ p 1 , N 2 ∈ p 2 a N 1 ∈ x 1,2 - obr. 6.6.Poznámka 6.2 Přímka, která je rovnoběžná s průmětnou, má jen jeden stopník.6.4 Obraz rovinyPravoúhlým průmětem roviny, která není kolmá k průmětně, je celá průmětna. Rovinu v Mongeověprojekci zadáme pomocí sdružených průmětů určujících prvků. Ukažme si nejobvyklejšízpůsoby určení roviny.1. Třemi body, které neleží v přímce (nekolineární body) - obr. 6.8.2. Dvěma různoběžkami - obr. 6.9. Sdružené průměty průsečíku různoběžek musí ležetna ordinále.

6.4. Obraz roviny 46Obrázek 6.8: Obrázek 6.9:Obrázek 6.10: Obrázek 6.11:3. Dvěma rovnoběžkami - obr. 6.10. Nárysem i půdorysem rovnoběžek jsou opět rovnoběžky(mohou ovšem i splývat).4. Bodem a přímkou - obr. 6.11. Aby byla rovina určena bodem a přímkou, nesmí bodležet na přímce.Speciálním případem je zadání roviny stopami. Stopa roviny ρ je přímka, ve které rovinaρ protne průmětnu. Průsečnice roviny ρ s nárysnou se nazývá nárysná stopa a značíme ji n ρ .Průsečnice roviny ρ s půdorysnou se nazývá půdorysná stopa a značíme ji p ρ .Stopy roviny jsou dvě přímky (rovnoběžné nebo různoběžné). Rovina určená stopami je tedyopět určena rovnoběžkami nebo různoběžkami.Pro půdorys nárysné stopy n ρ 1 a nárys půdorysné stopy p ρ 2 platí n ρ 1 = p ρ 2 = x 1,2 . Přímky n ρ 2a p ρ 1 se protínají na ose x 1,2 - obr. 6.12 nebo jsou obě rovnoběžné s osou x 1,2 .Příklad 6.3 V obrázku 6.13 rozhodneme, jakou polohu mají roviny, určené svými stopami,vzhledem k průmětnám.Řešení: Rovina α je v obecné poloze vzhledem k průmětnám, není kolmá ani rovnoběžnás žádnou z průměten. Rovina β je kolmá k nárysně, rovina γ je kolmá k půdorysně. Rovina σje kolmá k ose x a ρ je s x rovnoběžná. Posledním případem je rovina τ, která obsahuje osu x,v tomto případě není rovina stopami jednoznačně určena.□

6.4. Obraz roviny 47Obrázek 6.12:Obrázek 6.13:Poznámka 6.3 Rovina, která je rovnoběžná s průmětnou, má jen jednu stopu.V následujících kapitolách ukážeme 12 základních úloh, pomocí kterých budeme schopniřešit složitější konstrukce jako např. sestrojení těles v obecné poloze, jejich průniky či řezy naplochách. Každou složitější úlohu pak rozložíme na tyto základní úlohy, které už budeme umětřešit (provedeme dekompozici, což je velice důležitý postup plynoucí z analytického geometrickéhomyšlení).Rozdělíme úlohy na dva typy - polohové a metrické. Polohové úlohy řeší vztahy mezi jednotlivýmiútvary, jako je vzájemná poloha, průnik, rovnoběžnost. Vzdálenosti, velikost objektů,kolmost nám pomohou určit úlohy metrické.Uvedeme vždy důležité skutečnosti, které budeme využívat, a ukážeme přímo na příkladechřešení základních úloh.

6.5. Polohové úlohy 486.5 Polohové úlohy6.5.1 Přímka v rovině (základní úloha Z1)Při řešení tétonásledující fakta:úlohy je vhodné uvědomit si• Leží-li přímka v rovině, je se všemi přímkamiroviny různoběžná nebo rovnoběžná.• Stopník přímky ležící v rovině leží na jejístopě (Půdorysný stopník na půdorysnéstopě, nárysný stopník na nárysné stopě).• Chceme-li sestrojit stopu roviny, určímestopníky dvou přímek ležících v rovině.Půdorysná stopa je spojnicí půdorysnýchstopníků, nárysná stopa je spojnicínárysných stopníků. Obrázek 6.14:Obrázek 6.15: Obrázek 6.16:Příklad 6.4 Je dána rovina ρ a jeden průmět přímky k ležící v rovině ρ. Sestrojme druhýprůmět přímky k.a) Rovina ρ je učena přímkami a, b - obr. 6.15.b) Rovina ρ je učena stopami - obr. 6.17.Řešení: a) obr. 6.161. Sestrojíme průsečík A 1 přímky a 1 a k 1 .2. Sestrojíme průsečík B 1 přímky b 1 a k 1 .3. Odvodíme druhé průměty bodů A a B. Na přímce a 2 dostaneme bod A 2 a podobně bodB 2 .

6.5. Polohové úlohy 49Obrázek 6.17: Obrázek 6.18:4. Přímka k 2 je spojnicí bodů A 2 a B 2 .b) obr. 6.181. Sestrojíme nárys nárysného stopníku N 2 - průsečík přímky k 2 a stopy n ρ 2.2. Sestrojíme nárys půdorysného stopníku P 2 - průsečík přímky k 2 a osy x 1,2 = p ρ 2.3. Určíme body N 1 a P 1 , N 1 leží na ose x 1,2 a P 1 na stopě p ρ 1.4. Přímka k 1 je spojnicí bodů N 1 a P 1 .Hlavní přímky rovinyHlavní přímka roviny ρ je přímka, která leží v rovině ρ a je rovnoběžná s průmětnou.Horizontální hlavní přímka (hlavní přímka první osnovy) je rovnoběžná s půdorysnou.Speciálním případem horizontální hlavní přímky je půdorysná stopa. Všechny horizontálníhlavní přímky jedné roviny jsou navzájem rovnoběžné – obr. 6.19.□Obrázek 6.19: Obrázek 6.20:

6.5. Polohové úlohy 50Frontální hlavní přímka (hlavní přímka druhé osnovy) je rovnoběžná s nárysnou. Speciálnímpřípadem frontální hlavní přímky je nárysná stopa. Všechny frontální hlavní přímky jedné rovinyjsou navzájem rovnoběžné – obr. 6.20.Obrázek 6.21: Obrázek 6.22:Obrázek 6.23: Obrázek 6.24:Příklad 6.5 Zobrazte nějakou (libovolnou) a) horizontální hlavní přímku roviny ρ - obr. 6.21,b) frontální hlavní přímku roviny ρ - obr. 6.23.Řešení: a) (obr. 6.22) Horizontální hlavní přímka je rovnoběžná s půdorysnou, proto je jejínárys rovnoběžný s osou x 1,2 .1. Sestrojíme nárys přímky h. (h 2 ||x 1,2 ).2. Půdorys přímky h je rovnoběžný se stopou p ρ 1. Použijeme stopník N přímky h.Kdyby rovina nebyla určena stopami, odvodili bychom půdorys pomocí průsečíků s jinýmipřímkami roviny.b) (obr.6.24) Frontální hlavní přímka je rovnoběžná s nárysnou, proto je její půdorys rovnoběžnýs osou x 1,2 .1. Sestrojíme půdorys přímky f. (f 1 ||x 1,2 ).

6.5. Polohové úlohy 512. Nárys přímky f je rovnoběžný se stopou n ρ 2. Použijeme stopník P přímky f.Kdyby rovina nebyla určena stopami, odvodili bychom nárys pomocí průsečíků s jinými přímkamiroviny.□Spádové přímky rovinySpádová přímka je kolmá na hlavní přímky jednoho systému - obr. 6.25. To znamená, žemáme dva systémy spádových přímek - spádové přímky kolmé na horizontální hlavní přímky -spádové přímky první osnovy a spádové přímky kolmé na frontální hlavní přímky - spádovépřímky druhé osnovy.Příklad 6.6 Sestrojíme spádovou přímku s první osnovy (kolmou k horizontálním hlavnímpřímkám).Řešení: (obr. 6.26) Půdorys s 1 spádové přímky je kolmý k půdorysné stopě p ρ 1, což plyne z větyo pravoúhlém průmětu pravého úhlu. Najdeme půdorysy stopníků této přímky a odvodíme jedo nárysu. Nárys s 2 spádové přímky prochází nárysy těchto stopníků. Nárys spádové přímkynemá žádnou speciální polohu vůči stopám nebo ose x.□Obrázek 6.25: Obrázek 6.26:6.5.2 Bod v rovině (základní úloha Z2)Bod leží v rovině, právě když leží na některé přímce roviny. Chceme-li odvodit druhý průmětbodu ležícího v rovině, zvolíme přímku procházející tímto bodem (může to být i přímka hlavní)a použijeme řešení úlohy 6.5.1, tj. Z1. Bod leží na odvozené přímce a na ordinále.Příklad 6.7 Rovina ρ je určena přímkami a, b. Sestrojme nárys bodu M ležícího v rovině ρ,známe-li jeho půdorys - obr. 6.27.Řešení: (obr. 6.28)1. Bodem M 1 vedeme přímku k 1 , tím jsme úlohu převedli na úlohu 6.5.1, tj. Z1.

6.5. Polohové úlohy 52Obrázek 6.27: Obrázek 6.28:a) Sestrojíme průsečík A 1 přímky a 1 a k 1 .b) Sestrojíme průsečík B 1 přímky b 1 a k 1 .c) Odvodíme body A 2 a B 2 . Po ordinále na přímce a 2 dostaneme bod A 2 , na přímce b 2dostaneme bod B 2 .d) Přímka k 2 je spojnicí bodů A 2 a B 2 .2. Bod M 2 najdeme na přímce k 2 a na ordinále vedené bodem M 1 .□Obrázek 6.29: Obrázek 6.30:Příklad 6.8 Rovina ρ je určena stopami. Sestrojme půdorys bodu M ležícího v rovině ρ,známe-li jeho nárys - obr. 6.29.Řešení: (obr. 6.30)1. Bodem M 2 vedeme přímku k 2 , tím jsme úlohu převedli na úlohu 6.5.1, tj. Z1.a) Sestrojíme nárys nárysného stopníku N 2 - průsečík přímky k 2 a stopy n ρ 2.

6.5. Polohové úlohy 53b) Sestrojíme nárys půdorysného stopníku P 2 - průsečík přímky k 2 a osy x 1,2 = p ρ 2.c) Odvodíme body N 1 a P 1 , N 1 leží na ose x 1,2 a P 1 na stopě p ρ 1.d) Přímka k 1 je spojnicí bodů N 1 a P 1 .2. Bod M 1 najdeme na přímce k 1 a na ordinále vedené bodem M 2 .6.5.3 Rovnoběžné roviny (základní úloha Z3)□Při řešení této úlohy je vhodné uvědomit sinásledující fakta:• Kritérium rovnoběžnosti přímky a roviny.Kritérium rovnoběžnosti dvou rovin.• Rovnoběžné roviny mají rovnoběžnéstopy.• Stopy roviny obecně neprochází nárysemi půdorysem bodu ležícím v této rovině(aby nastal tento případ, musel by bodležet na ose x). Obrázek 6.31:Obrázek 6.32: Obrázek 6.33:Příklad 6.9 Rovina ρ je určena přímkami a, b. Bodem M ved’te rovinu σ rovnoběžnou srovinou ρ - obr. 6.32.Řešení: (obr.6.33)

6.5. Polohové úlohy 541. Bodem M vedeme přímku a ′ rovnoběžnou s přímkou a (a ′ 1||a 1 , a ′ 2||a 2 ).2. Bodem M vedeme přímku b ′ rovnoběžnou s přímkou b (b ′ 1||b 1 , b ′ 2||b 2 ).3. Přímkami a ′ b ′ je určena rovina σ.□Obrázek 6.34: Obrázek 6.35:Příklad 6.10 Rovina ρ je určena stopami. Bodem M ved’te rovinu σ rovnoběžnou s rovinouρ - obr.6.34. Sestrojte stopy roviny σ.Řešení: (obr. 6.35)1. Bodem M vedeme hlavní přímku h rovnoběžnou s půdorysnou stopou roviny ρ (h 1 ||p ρ 1,h 2 ||p ρ 2 = x 1,2 ).2. Bodem M vedeme hlavní přímku f rovnoběžnou s nárysnou stopou roviny ρ (f 2 ||n ρ 2,f 1 ||n ρ 1 = x 1,2 ).3. Přímkami h, f je určena rovina σ.4. Pro sestrojení stop roviny σ nám stačí nalézt stopník jedné z přímek h f - našli jsmepůdorysný stopník P přímky f.5. Půdorysná stopa roviny σ prochází půdorysným stopníkem a je rovnoběžná s půdorysnoustopou roviny ρ.6. Nárysná stopa roviny σ je rovnoběžná s nárysnou stopou roviny ρ a protíná se s půdorysnoustopou na ose x.6.5.4 Průsečík přímky s rovinou (základní úloha Z4)Příklad 6.11 Rovina σ je určena přímkami a, b. Sestrojte průsečík přímky p s rovinou σ - obr.6.37.Řešení: (obr. 6.38)□

6.5. Polohové úlohy 55Pro určení průsečíku přímky s rovinoupoužijeme metodu krycí přímky. V roviněσ zvolíme přímku s, která se kryje s přímkoup v některém průmětu, tj. leží s přímkou pv jedné promítací rovině, a zároveň leží vrovině σ. Přímka s je průsečnicí roviny σ apromítací roviny přímky p. Průsečík přímky pa s je zároveň průsečíkem přímky p s rovinouσ. V průmětně, ve které průměty přímek p a snesplývají, najdeme jejich průsečík a odvodímepomocí ordinály do druhé průmětny. Obrázek 6.36:1. V rovině σ zvolíme půdorysně krycí přímku s (s 1 = p 1 , s ⊂ σ).2. Pomocí průsečíků přímky s s přímkami a, b odvodíme přímku s 2 (úloha 6.5.1, tj. Z1).3. Průsečík P 2 přímek p 2 a s 2 je nárysem hledaného průsečíku přímky p s rovinou σ.4. Půdorys P 1 průsečíku najdeme na přímce p 1 a na ordinále vedené bodem P 2 .□Obrázek 6.37: Obrázek 6.38:Příklad 6.12 Rovina σ je určena stopami. Sestrojte průsečík přímky p s rovinou σ - obr. 6.39.Řešení: (obr. 6.40)1. V rovině σ zvolíme nárysně krycí přímku s (s 2 = p 2 , s ⊂ σ).2. Pomocí stopníků odvodíme přímku s do půdorysu (úloha 6.5.1, tj. Z1).3. Průsečík P 1 přímek p 1 a s 1 je půdorysem hledaného průsečíku přímky p s rovinou σ.4. Nárys P 2 průsečíku najdeme na přímce p 2 a na ordinále vedené bodem P 1 .□

6.5. Polohové úlohy 56Obrázek 6.39: Obrázek 6.40:6.5.5 Průsečnice dvou rovin (základní úloha Z5)• Pokud přímka r leží v rovině ρ, pakprůsečík R přímky r s rovinou σ leží naprůsečnici p rovin ρ a σ.• Průsečnice rovin je přímka ležící v obourovinách, tj. její stopník leží na stopáchobou rovin.Obrázek 6.41:Příklad 6.13 Roviny ρ a σ jsou určeny stopami. Sestrojte průsečnici těchto rovin - obr. 6.42.Řešení: (obr. 6.43)1. Nárysný stopník průsečnice leží na nárysné stopě roviny ρ i roviny σ.(N 2 ∈ n ρ 2 ∩ n σ 2, N 1 ∈ x 1,2 ).2. Půdorysný stopník průsečnice leží na půdorysné stopě roviny ρ i roviny σ.(P 1 ∈ p ρ 1 ∩ p σ 1, P 2 ∈ x 1,2 ).3. Přímka NP je hledanou průsečnicí.Příklad 6.14 Rovina ρ je určena přímkami r a q a rovina σ je dána stopami. Sestrojteprůsečnici těchto rovin - obr. 6.44.□

6.5. Polohové úlohy 57Obrázek 6.42: Obrázek 6.43:Obrázek 6.44: Obrázek 6.45:Řešení: (obr. 6.45) Vyřešíme dvakrát úlohu průsečík přímky s rovinou.1. Zvolíme krycí přímku s, tak aby s 2 = q 2 a s ⊂ σ.2. Odvodíme půdorys s 2 přímky s. (Úloha 6.5.1).3. Najdeme průsečík X 1 přímek s 1 a q 1 .4. Odvodíme bod X do nárysu na přímku q.5. Podobně zvolíme krycí přímku u a najdeme průsečík Y .6. Přímka XY je hledaná průsečnice.Poznámka 6.4 Všimněte si, že v některých úlohách jsme ke konstrukcím nepoužívali osu x 1,2 ,stačilo nám znát směr ordinály. Vzpomeneme si, že kolmé průměty téhož objektu do rovnoběžnýchrovin jsou shodné. Pokud tedy nezáleží na vzdálenosti od průměten, můžeme osu xvynechat, případně posunout průměty ve směry ordinály. Je to výhodné zejména v případech,kdy se nárys a půdorys překrývají a chceme zobrazení zpřehlednit.Není-li zadaná osa x, nemůžeme používat stopy a stopníky.□

6.6. Metrické úlohy 586.6 Metrické úlohy6.6.1 Skutečná velikost úsečky (základní úloha Z6)Na obrázku 6.46 je zřejmé, že body A, B a jejich průměty do půdorysny tvoří lichoběžníkABB 1 A 1 s pravými úhly při vrcholech A 1 a B 1 . V tomto lichoběžníku známe, kromě pravýchúhlů, také velikost strany A 1 B 1 , a velikosti stran AA 1 (z-ová souřadnice bodu A) a BB 1 (zovásouřadnice bodu B). Tento lichoběžník zobrazíme pomocí sklopení promítací roviny dopůdorysny. Podobně můžeme provést sklopení do nárysny.Obrázek 6.46:Obrázek 6.47: Obrázek 6.48:Příklad 6.15 Sestrojte skutečnou velikost úsečky AB - obr. 6.47.Řešení: (obr. 6.48)1. z A (zetovou souřadnici bodu A) naneseme na kolmici vedenou bodem A 1 , získaný bodoznačíme (A).2. z B (zetovou souřadnici bodu B) naneseme na kolmici vedenou bodem B 1 , získaný bodoznačíme (B).

6.6. Metrické úlohy 593. Spojnice bodů (A), (B) je sklopená přímka b. Vzdálenost bodů (A), (B) je skutečnávelikost úsečky AB.Poznámka 6.5 Mají-li body A, B opačná znaménka souřadnice z, pak body ABB 1 A 1 netvořílichoběžník, ale čtyřúhelník, ve kterém se dvě strany protínají. Při sklápění tohoto čtyřúhelníkunaneseme příslušné souřadnice na opačně orientované kolmice.Poznámka 6.6 Je-li body A, B je určena přímka p, pak sklopená přímka (p) je určena body(A)(B). Odchylka přímky od půdorysny je rovna odchylce přímek p(p).Postup pro určování skutečné velikosti úsečky si můžeme zjednodušit použitím metodyrozdílového trojúhelníka. V obrázku 6.46 je vyznačen pravoúhlý trojúhelník A 1 B 1 (B) ∗ spravým úhlem při vrcholu B 1 . Úsečky (A)(B) a A 1(B) ∗ jsou rovnoběžné a shodné. Stačí tedy sestrojittento rozdílový trojúhelník, kde velikost strany B 1 (B) ∗ je rovna rozdílu z-ových souřadnicbodů A a B.I tento postup lze analogicky použít pro nárys, na kolmici k úsečce A 2 B 2 ovšem nanesemerozdíl y-ových souřadnic bodů A a B.□Obrázek 6.49: Obrázek 6.50:Příklad 6.16 Sestrojte skutečnou velikost úsečky AB použitím rozdílového trojůhelníka - obr.6.49.Řešení: (obr. 6.50) Pomocí rozdílového trojúhelníka.1. Na kolmici vedenou bodem B 1 naneseme |z A − z B |, získaný bod označíme (B).2. Spojnice bodů (B), A 1 je sklopená úsečka AB a vzdálenost bodů (B), A 1 je skutečnávelikost úsečky AB.Je zřejmé, že velikost úsečky rovněž zjistíme, vedeme-li kolmici bodem A (a není přitom důležité,do které poloroviny sklápíme). Ve všech případech vyjdou shodné trojúhelníky, které majíshodné přepony. Uvedený postup používá místo absolutních souřadnic souřadnice relativní.Použití relativních souřadnic vede k možnosti vynechání základnice.□

6.6. Metrické úlohy 606.6.2 Nanesení úsečky na přímku (základní úloha Z7)Sklápění, které jsme využili v úloze 6.6.1, využijeme i v této úloze. Zvolíme na přímce dva bodya sklopíme ji. Na sklopenou přímku naneseme úsečku ve skutečné velikosti a sklopíme zpět.Při sklápění použijeme metodu rozdílového trojúhelníka.Obrázek 6.51: Obrázek 6.52:Příklad 6.17 Je dána přímka b a na ní bod A. Naneste na přímku b od bodu A vzdálenost u- obr. 6.51.Řešení: (obr. 6.52)1. Zvolíme na přímce b bod X ≠ A.2. Sklopíme úsečku AX (použitím úlohy Z6 z odst. 6.6.1):(a) Na kolmici vedenou bodem X 2 naneseme |z X − z A |, získaný bod označíme (X).(b) Spojnice bodů (X), A 2 je sklopená přímka b.3. Na sklopenou přímku b naneseme velikost u, získaný bod označíme (B).4. Bod (B) sklopíme zpět na přímku b 2 pomocí kolmice vedené bodem (B) k přímce b 2 .Dostáváme bod B 2 .5. Bod B 1 odvodíme po ordinále na přímku b 1 .6. Úsečka AB má skutečnou velikost u.6.6.3 Přímka kolmá k rovině (základní úloha Z8)Při hledání přímky kolmé k rovině je vhodné si přípomenout:• Kritérium kolmosti přímky a roviny.• Větu o průmětu pravého úhlu.□

6.6. Metrické úlohy 61Obrázek 6.53:Obrázek 6.54: Obrázek 6.55:• Protože h||π, tak k 1 ⊥ h 1 .• Protože f||ν, tak k 2 ⊥ f 2 .Příklad 6.18 Rovina ρ je určena hlavními přímkami h, f. Sestrojte kolmici k bodem M k roviněρ - obr. 6.54.Řešení: (obr. 6.55)1. Bodem M 1 vedeme kolmici k 1 k přímce h 1 .2. Bodem M 2 vedeme kolmici k 2 k přímce f 2 .Příklad 6.19 Rovina ρ je určena přímkami p, q. Sestrojte kolmici k bodem M k rovině ρ -obr. 6.56.Řešení: (obr. 6.57)□

6.6. Metrické úlohy 62Obrázek 6.56: Obrázek 6.57:1. Sestrojíme libovolné hlavní přímky h, f roviny ρ.a) Přímka f 1 je rovnoběžná s x 1,2 , f 2 odvodíme pomocí průsečíků přímky f s p a q.b) Přímka h 2 je rovnoběžná s x 1,2 , h 1 odvodíme pomocí průsečíků přímky h s p a q.2. Postupujeme jako v předchozí úloze.a) Bodem M 1 vedeme kolmici k přímce h 1 , dostaneme k 1 .b) Bodem M 2 vedeme kolmici k přímce f 2 , dostaneme k 2 .6.6.4 Rovina kolmá k přímce (základní úloha Z9)Tato úloha je obrácená k úloze předchozí, využijeme opět znalostí kritéria kolmosti přímky k roviněa hlavních přímek. Uvědomíme si, že nárys horizontální hlavní hlavní přímky je rovnoběžnýs osou x 1,2 (neboli kolmý na ordinály) a půdorys je kolmý k zadané přímce. Pro frontální hlavnípřímku platí, že půdorys je rovnoběžný s osou x 1,2 a nárys je kolmý k zadané přímce.Tedy h 1 ⊥ p 1 a h 2 ||x 1,2 a f 2 ⊥ p 2 a f 1 ||x 1,2 .Hlavní přímky v této úloze proto neodvozujeme pomocí průsečíků, ale sestrojujeme kolmicek průmětům zadané přímky! Je totiž zřejmé, že hlavní přímky jsou zpravidla s danou přímkoumimoběžné, a tudíž průsečíky v prostoru neexistují.Příklad 6.20 Je dána přímka p. Sestrojíme bodem M rovinu kolmou k přímce p - obr. 6.58.Řešení: (obr. 6.59) Sestrojíme hlavní přímky hledané roviny σ.1. h 1 ⊥ p 1 a h 2 ||x 1,2 a M 1 ∈ h 1 , M 2 ∈ h 2 .2. f 2 ⊥ p 2 a f 1 ||x 1,2 a M 1 ∈ f 1 , M 2 ∈ f 2 .3. Rovina σ je určena přímkami h, f.□□

6.6. Metrické úlohy 63Obrázek 6.58: Obrázek 6.59:6.6.5 Otočení roviny do polohy rovnoběžné s průmětnou (základníúloha Z10)nnC 2CC 1rp 1SC 0pxCC 1C 2ShC 0pxa) b)Obrázek 6.60:Často je součástí prostorové konstrukce rovinná úloha. Potřebujeme například sestrojitpodstavu nějakého tělesa v obecné rovině α. Víme, že útvar ležící v rovině rovnoběžné sprůmětnou se promítne ve skutečné velikosti. Otočíme tedy rovinu α (některé její body) dopolohy rovnoběžné s průmětnou π (obr. 6.60b)) nebo přímo do průmětny (obr. 6.60a)), provedemepožadovanou konstrukci a výsledek otočíme zpět.Nejprve musíme určit přímku, kolem které budeme rovinu α otáčet. V případě, že otáčímepřímo do průmětny, je osou otáčení průsečnice rovin α a π, tedy stopa roviny α (obr. 6.60a)).Nemáme-li zadanou osu x nebo chceme-li si ušetřit práci se sestrojováním stopy, můžeme otočitrovinu α do polohy rovnoběžné s průmětnou kolem přímky rovnoběžné s průmětnou, tedyhlavní přímky roviny α (obr. 6.60b)).Mezi body roviny α a body otočenými do průmětny existuje prostorová geometrická příbuznost- osová afinita. Víme, že rovnoběžným průmětem osové afinity získáme osovou afinitu v rovině,

6.6. Metrické úlohy 64odtud plyne, že při konstrukcích můžeme využívat osové afinity mezi průměty bodů (napříkladpůdorysy) a otočenými body do téže průmětny (půdorysny). Osou afinity je osa otáčení, páremodpovídajících si bodů je průmět bodu (např. A 1 ) a jeho otočený obraz A 0 .Postup řešení rovinné úlohy je následující:1. Určíme osu otáčení - hlavní přímka nebo stopa roviny.2. Sestrojíme rovinu, střed a poloměr kružnice otáčení (příklad 1.1 na straně 9).3. Otočíme jeden bod.4. Další otočené body získáme pomocí afinity.5. Provedeme rovinnou konstrukci.6. S využitím afinity otočíme výsledek zpět.7. Body výsledného útvaru odvodíme do druhého průmětu.Obrázek 6.61: Obrázek 6.62:Příklad 6.21 Otočme rovinu α kolem stopy do průmětny - obr. 6.61.Řešení: (obr. 6.62) Otočíme jeden bod roviny α.1. Pomocí horizontální hlavní přímky h roviny α vedené bodem C odvodíme půdorys boduC.2. Budeme otáčet do půdorysny, tj. osou otáčení je půdorysná stopa p α 1 .3. Rovina otáčení ρ bodu C se promítá do přímky k 1 procházející bodem C 1 a kolmé k oseotáčení p α 1 .4. Střed otáčení S je průsečík roviny ρ se stopou, tedy S 1 je průsečíkem přímky k 1 se stopoup α 1 .5. Poloměr otáčení r je skutečná velikost úsečky CS. Skutečnou velikost úsečky určímesklopením - na kolmici k úsečce C 1 S 1 naneseme (relativní) zetovou souřadnici boduC (tj. rozdíl zetových souřadnic bodů C a S, S má zetovou souřadnici 0, protože ležív půdorysně).

6.6. Metrické úlohy 65C 2C 1k 1S 1C 0h 2h 1Obrázek 6.63:Obrázek 6.64:6. Na kolmici k 1 naneseme od bodu S 1 poloměr r, dostaneme tak otočený bod C 0 .Příklad 6.22 Otočme rovinu α, určenou bodem C a hlavní přímkou h, kolem h do rovinyrovnoběžné s průmětnou - obr. 6.63.Řešení: (obr. 6.64) Otočíme jeden bod roviny α.1. Otočíme rovinu α kolem hlavní přímky h do polohy rovnoběžné s půdorysnou.2. Osou otáčení je hlavní přímka h.3. Bodem C 1 vedeme kolmici k 1 k přímce h 1 (rovina otáčení se promítá do k 1 ).4. Průsečík přímky k 1 s h 1 je půdorysem středu otáčení S.5. Sklopíme úsečku CS a zjistíme skutečnou velikost poloměru otáčení r (na kolmici k C 1 S 1naneseme rozdíl zetových souřadnic bodu CS a přímky h).6. Od bodu S 1 naneseme na k 1 poloměr r a získáme otočený bod C 0 .Příklad 6.23 V rovině ρ jsou dány body A a C svými nárysy. Sestrojíme čtverec ABCDs úhlopříčkou AC ležící v rovině ρ - obr. 6.65.Řešení: (obr. 6.66) Sestrojení čtverce je rovinná úloha. Rovinu ρ otočíme do půdorysny, sestrojímečtverec v otočení a výsledek otočíme zpět.1. Pomocí hlavní přímky odvodíme bod C do půdorysu, půdorys bodu A leží na ose x 1,2 .2. Otočíme bod C do půdorysny - získáme bod C 0 .3. Bod A 0 sestrojíme pomocí afinity (osa afinity je p ρ 1, pár odpovídajících si bodů je A 1 , A 0 .4. V otočení sestrojíme čtverec A 0 B 0 C 0 D 0 .5. Pomocí afinity otočíme čtverec zpět do půdorysu. (Můžeme využít rovnoběžnosti protějšíchstran.)6. S využitím hlavních přímek najdeme nárys čtverce.□□□

6.6. Metrické úlohy 66Obrázek 6.65: Obrázek 6.66:6.6.6 Obraz kružnice (základní úloha Z11)Podívejme se, jak se v pravoúhlém promítání zobrazí kružnice. Pokud kružnice leží v roviněrovnoběžné s průmětnou, bude jejím obrazem shodná kružnice. Obrazem kružnice ležící v roviněkolmé na průmětnu bude úsečka, jejíž délka je rovna průměru kružnice. Obrazem kružnicev obecném případě je elipsa. Velikost průměru kružnice, který leží na hlavní přímce, se připravoúhlém promítání zachová, ostatní průměry se v pravoúhlém promítání zkracují. Průměrna hlavní přímce bude tedy hlavní osou elipsy, do které se kružnice zobrazí.Obrázek 6.67: Obrázek 6.68:

6.6. Metrické úlohy 67Příklad 6.24 V rovině ρ(h, f) sestrojme kružnici k(S, r) - obr. 6.67.Řešení: (obr. 6.68)1. Na horizontální hlavní přímku h naneseme v půdorysu od bodu S 1 na obě strany skutečnouvelikost poloměru r - body označíme A 1 , B 1 a odvodíme je po ordinále do nárysu.2. Na frontální hlavní přímku f naneseme v nárysu od bodu S 2 na obě strany skutečnouvelikost poloměru r - body označíme C 2 , D 2 a odvodíme je po ordinále do půdorysu.3. Obrazem kružnice v půdorysu je elipsa s hlavní osou A 1 B 1 , body C 1 , D 1 leží na elipse.Pomocí proužkové konstrukce získáme vedlejší osu.4. Obrazem kružnice v nárysu je elipsa s hlavní osou C 2 D 2 , body A 2 , B 2 leží na elipse.Pomocí proužkové konstrukce získáme vedlejší osu.6.6.7 Transformace průměten (základní úloha Z12)V předchozích úlohách jsme již mluvili o možnosti vynechání osy x, to znamená o posunutípůdorysny nebo nárysny. Nárys nebo půdorys útvarů se neměnil, nebot’ poloha nových průmětenbyla rovnoběžná s původními.Nyní přejdeme od původních průměten k nové dvojici navzájem kolmých průměten. Jednuprůmětnu necháme v původní poloze a jako druhou volíme libovolnou rovinu k ní kolmou(volíme ji vhodně tak, aby se použitím nových průměten úloha zjednodušila).Zvolíme například třetí průmětnu µ kolmou k půdorysně π – obr. 6.69. Průsečnice rovinµ a π bude novou osou x - označíme ji x 1,3 . Promítneme bod M do třetí průmětny, průmětoznačíme indexem M 3 a provedeme sdružení průmětů. Ordinála bude spojnicí bodů M 1 a M 3a bude kolmá k ose x 1,3 , vzdálenost M 3 od osy x 1,3 je z-ovou souřadnicí bodu M - obr. 6.70.□Obrázek 6.69: Obrázek 6.70:Příklad 6.25 Určeme vzdálenost bodu A od roviny ρ s využitím třetí průmětny (obr. 6.71).Řešení: (obr. 6.72)

6.7. KontrolnÍ otázky 68Obrázek 6.71: Obrázek 6.72:1. Zvolíme třetí průmětnu µ kolmou k půdorysně a kolmou k rovině ρ - rovina ρ se do novéprůmětny zobrazí jako přímka.2. Najdeme třetí průmět bodu A.3. Najdeme třetí průmět libovolného bodu roviny ρ - zvolili jsme stopník N.4. Třetím průmětem roviny ρ je přímka procházející bodem N 3 a protínající se se stopou p ρ 1na ose x 1,3 .5. Vzdálenost A 3 a ρ 3 je hledanou vzdáleností bodu A od roviny ρ.□6.7 Kontrolní otázky6.1 Definujte pojem stopník a stopa.6.2 Vysvětlete pojem hlavní přímka.6.3 Vysvětlete metodu krycí přímky.6.4 K čemu se používá otáčení roviny?6.5 V čem se liší otáčení roviny okolo stopy a okolo hlavní přímky?

Kapitola 7Axonometrie7.1 ÚvodPředpokládejme, že je v prostoru dána kartézská soustava souřadnic. Souřadnicové rovinynazýváme půdorysna - xy ( 1 π), nárysna xz ( 2 π) a bokorysna yz ( 3 π). V praxi obvykle umíst’ujemeobjekty co nejvýhodněji vzhledem k osám. Např. hranol nebo válec umístíme tak, aby měl podstavuv souřadnicové rovině. Útvar, který má osu, umístíme tak, aby jeho osa byla rovnoběžnás osou soustavy souřadnic. Jestliže promítneme pravoúhle tento objekt do souřadnicových rovin(Mongeova projekce), budou se nám snadno řešit polohové a metrické úlohy, ale chybí názornýpohled. Názornou zobrazovací metodou, která využívá výhody rovnoběžného promítání, je axonometrie.Obrázek 7.1:Axonometrie je rovnoběžné promítání na jednu průmětnu α takové, že směr promítání snení rovnoběžný s žádnou souřadnicovou rovinou, tj. osy se promítají do tří různých přímekx A , y A , z A - obr.7.1.Rovinu α nazýváme axonometrickou průmětnou; x A , y A , z A axonometrickými průmětyos x, y, z; B A axonometrickým průmětem bodu B. Pravoúhlé průměty bodu B dosouřadnicových rovin jsou půdorys (xy), nárys (xz) a bokorys (yz) a jejich průměty do axonometricképrůmětny axonometrický půdorys (B 1A ), nárys (B 2A ) a bokorys (B 3A ). Jednotky69

7.2. Klasifikace axonometriÍ 70na osách (j x , j y , j z ) se promítnou do axonometrických jednotek (j xA , j yA , j zA ).Chceme-li zadat axonometrii, vycházíme z následující věty:Věta 7.1 (Pohlkeova věta) Tři úsečky se společným koncovým bodem, které leží v jedné roviněa neleží na jedné přímce, můžeme považovat za rovnoběžný průmět tří navzájem kolmých ashodných úseček v prostoru.7.2 Klasifikace axonometriíPodle velikosti axonometrických jednotek j x , j y , j z :1. izometrie ( j x = j y = j z ) - obr. 7.2a)2. dimetrie ( j x = j y nebo j y = j z nebo j x = j z ) - obr. 7.2b)3. trimetrie ( j x ≠ j y ≠ j z ) - obr. 7.2c)zzzj xj xyj yObrázek 7.2:j yyxj xxxa) b) c)yPodle směru promítání1. Směr s je kolmý k axonometrické průmětně, axonometrie se nazývá pravoúhlá.2. Směr s není kolmý k axonometrické průmětně, axonometrie se nazývá obecná nebo takékosoúhlá.Uved’me si ještě některé speciální axonometrie:1. Kosoúhlé promítání. Průmětnou je souřadnicová rovina yz a směr není kolmý k průmětně.Na osách y a z jsou jednotky stejné, na ose x se jednotka obvykle zkracuje. Je to dimetrienebo izometrie.2. Vojenská perspektiva. Průmětnou je souřadnicová rovina xy a směr není kolmý kprůmětně. Na všech osách je stejné zkrácení jednotek. Promítání je izometrie.3. Pravoúhlá axonometrie. Průmětnou je obecná rovina, která protíná osy v bodechrůzných od počátku. Směr je kolmý k průmětně. Pravoúhlou axonometrií se budeme ještěpodrobněji zabývat, protože má některé pěkné vlastnosti.

7.3. ZobrazenÍ bodu 717.3 Zobrazení boduJedním průmětem není bod v prostoru jednoznačně určen, proto musíme k axonometrickémuprůmětu zadávat ještě některý z pravoúhlých průmětů do souřadnicových rovin. Obvyklé jezadání dvojicí B A a B 1A . Bod však může být určen libovolnou dvojicí z bodů B A , B 1A , B 2A ,B 3A (např. B 1A , B 3A ).Na obrázku 7.3 je axonometrický obrazbodu B[2, 3, 4], jeho axonometrický nárys,půdorys a bokorys.Obrázek 7.3:Poznámka 7.1 Pro zjednodušení budemetam, kde nemůže dojít k záměně, axonometricképrůměty označovat bez dolního indexuA a vynechávat přívlastek axonometrický.Obrázek 7.4: Obrázek 7.5:Příklad 7.1 Bod je v axonometrii určen dvojicí A a A 3 - obr. 7.4. Doplníme zbývající pravoúhléprůměty do souřadnicových rovin.Řešení: (obr.7.5) Pomocí rovnoběžek s osami x, y, z doplníme zbývající průměty.Příklad 7.2 Zobrazíme body A ∈ xy, B ∈ yz, C ∈ xz - obr. 7.6.Řešení: (obr.7.7)A ∈ xy ⇒ A = A 1 , A 2 ∈ x, A 3 ∈ yB ∈ yz ⇒ B = B 3 , B 2 ∈ z, B 1 ∈ yC ∈ xz ⇒ C = C 2 , C 1 ∈ x, C 3 ∈ z□□

7.4. ZobrazenÍ přÍmky 72Obrázek 7.6: Obrázek 7.7:7.4 Zobrazení přímkyPřímka je určena dvěma body, průmět přímky je tedy určen průměty dvou bodů.Obrazem přímky p, která není kolmá k průmětně, je opět přímka. Zadáváme ji opět pomocíaxonometrického průmětu p A a pravoúhlého průmětu do souřadnicové roviny (např. p 1A ).Stopník je opět průsečík přímky s průmětnou, ovšem v tomto případě s průmětnou axonometrickou.Tento stopník ale v konstrukcích zpravidla nevyužíváme. Výhodné jsou pro nás pomocnéstopníky, jimiž jsou průsečíky přímky se souřadnicovými rovinami (xy, xz, yz). Nazývámeje půdorysný, nárysný a bokorysný stopník.Obrázek 7.8: Obrázek 7.9:Příklad 7.3 Sestrojíme půdorysný, nárysný a bokorysný stopník přímky a - obr. 7.8.Řešení: (obr.7.9)Průsečík přímky a a jejího půdorysu a 1 je půdorysný stopník P = P 1 .Průsečík přímky a 1 s osou x je půdorys nárysného stopníku N 1 , nárysný stopník N najdemena přímce a a na rovnoběžce s osou z vedené bodem N 1 .

7.5. ZobrazenÍ roviny 73Průsečík přímky a 1 s osou y je půdorys bokorysného stopníku M 1 , bokorysný stopník Mnajdeme na přímce a a na rovnoběžce s osou z vedené bodem M 1 .□7.5 Zobrazení rovinyRovinu můžeme určit pomocí průmětů prvků, které ji určují (např. třemi různými nekolineárnímibody, dvěma rovnoběžkami, dvěma různoběžkami nebo přímkou a bodem, kterýna ní neleží). Nejnázornější je zadání roviny pomocí stop. Stopa roviny je průsečnice rovinys průmětnou, ale my budeme (stejně jako u stopníků) používat průsečnice roviny sesouřadnicovými rovinami (xy, xz, yz). Nazýváme je půdorysná, nárysná a bokorysná stopa.Obrázek 7.10: Obrázek 7.11:Každá dvojice stop se protíná na ose (průsečík může být i nevlastní bod, tj. stopy jsou pakrovnoběžné). Pro určení roviny stačí zadat dvě stopy, jsou to dvě různoběžné nebo rovnoběžnépřímky. Třetí stopu snadno doplníme pomocí průsečíků s osami - obr. 7.10 nebo 7.11.Obrázek 7.12: Obrázek 7.13:

7.6. Úlohy v axonometrii 74Na obrázku 7.12 jsou stopy roviny ρ rovnoběžné s půdorysnou xy, stopy roviny σ rovnoběžnés bokorysnou yz a stopy roviny τ rovnoběžné s nárysnou yz. Na obrázku 7.13 jsou stopy rovinyα kolmé na nárysnu xz, stopy roviny β kolmé na půdorysnu xy a stopy roviny γ kolmé nabokorysnu yz.7.6 Úlohy v axonometriiV obecné axonometrii se zaměříme pouze na polohové úlohy a ukážeme si, jak lze zobrazitkružnici. Další typy úloh jsou nejen příliš složité, ale zejména jejich řešení umožňuje Mongeovaprojekce. Pomocí přepočtu délek na osách pak může být zobrazen v axonometrii jen výsledek.Obrázek 7.14:7.6.1 Vzájemná poloha přímekZ axonometrických průmětů přímek a jejich půdorysů můžeme určit jejich vzájemnou polohu.Z vlastností rovnoběžného promítání plyne, že rovnoběžné přímky se budou promítat jakorovnoběžky (pokud se nepromítnou jako dva body). Rovnoběžné budou jak jejich axonometricképrůměty, tak jejich půdorysy - obr. 7.14a). Na obrázku 7.14b) jsou různoběžky, průsečík jejichaxonometrických průmětů a půdorysů leží na rovnoběžce s osou z (můžeme ji říkat ordinála)na rozdíl od mimoběžek - obr. 7.14c).7.6.2 Přímka v roviněPřipomeňme důležité vlastnosti:• Přímka ležící v rovině je se všemi ostatními přímkami rovnoběžná nebo různoběžná.• Přímka leží v rovině, právě když všechny stopníky přímky leží na příslušných stopáchroviny.Těchto vlastností využijeme i v následujících úlohách.

7.6. Úlohy v axonometrii 75Obrázek 7.15: Obrázek 7.16:Příklad 7.4 Je dána rovina ρ. Sestrojme axonometrický průmět přímky m ∈ ρ, je-li dán jejípůdorys m 1 - obr. 7.15.Řešení: (obr.7.16)1. Najdeme průsečík přímky m 1 s půdorysnou stopou p ρ 1 roviny ρ, získali jsme půdorysnýstopník P = P 1 .2. Průsečík přímky m 1 s osou y je půdorys bokorysného stopníku M 1 .3. Bokorysný stopník M najdeme na bokorysné stopě m ρ a na rovnoběžce s osou z vedenébodem M 1 . (Podobně bychom mohli sestrojit i nárysný stopník, ale pro konstrukci přímkystačí kterékoliv dva ze tří stopníků.)4. Oba stopníky leží na přímce m, axonometrický průmět přímky m je proto jejich spojnicí.(Nárysný stopník by ležel na také na přímce m.)□Obrázek 7.17: Obrázek 7.18:

7.6. Úlohy v axonometrii 76Příklad 7.5 Je dána rovina ρ(a, b). Sestrojte m 1 , je-li dán axonometrický průmět přímky m ∈ρ - obr. 7.17.Řešení: (obr.7.18)1. Najdeme průsečíky A, B přímky m s přímkami a, b.2. Body A, B odvodíme na přímky a 1 a b 1 a získáme jejich půdorysy A 1 a B 1 .3. Přímka m 1 prochází body A 1 a B 1 .7.6.3 Průsečík přímky s rovinouPrůsečík přímky k s rovinou ρ budeme opět hledat metodou krycí přímky. Podobně jako vMongeově projekci volíme krycí přímku s tak, aby krycí přímka ležela v rovině ρ. Máme dvěmožnosti volby této krycí přímky: bud’ se kryjí axonometrické průměty přímek k a s a hledámeprůsečík jejich půdorysů nebo se kryjí půdorysy a hledáme průsečík axonometrických průmětůpřímek k a s. V následujících dvou příkladech jsme volili první možnost.□Obrázek 7.19: Obrázek 7.20:Příklad 7.6 Sestrojíme průsečík přímky k s rovinou ρ, určenou stopami - obr. 7.19.Řešení: (obr. 7.20)1. Volíme krycí přímku s tak, že axonometrické průměty přímek s a k splynou a s ⊂ ρ.2. Odvodíme půdorys přímky s pomocí stopníků N a M. Půdorys přímky s označíme s 1 .3. Průsečík přímek s 1 a k 1 je půdorysem hledaného průsečíku P 1 . Axonometrický průmětbodu P odvodíme pomocí ordinály (rovnoběžky s osou z).Příklad 7.7 Sestrojíme průsečík přímky k s rovinou ρ, určenou stopami - obr. 7.21.□

7.6. Úlohy v axonometrii 77Řešení: (obr. 7.22)Obrázek 7.21: Obrázek 7.22:1. Volíme krycí přímku s tak, že axonometrické průměty přímek s a k splynou a s ⊂ ρ.2. Odvodíme půdorys přímky s pomocí průsečíků A, B s přímkami a a b. Půdorys přímkys označíme s 1 .3. Průsečík přímek s 1 a k 1 je půdorysem hledaného průsečíku P 1 . Axonometrický průmětbodu P odvodíme pomocí ordinály (rovnoběžky s osou z).7.6.4 Průsečnice rovinJsou dány roviny ρ a σ. Pokud je alespoň jedna z rovin, např. ρ, určena obecně zadanýmipřímkami, najdeme dvakrát průsečík přímky s rovinou σ a jejich spojnice je průsečnicí zadanýchrovin.Jednodušší situaci máme, jestliže jsou obě roviny zadané stopami. Poznamenejme, že stopyroviny umíme najít pomocí stopníků. Půdorysné stopy obou rovin leží v rovině xy. Jejichprůsečík je půdorysný stopník hledané průsečnice. Podobně můžeme najít nárysný stopníkjako průsečík nárysných stop a bokorysný stopník jako průsečík bokorysných stop. Pro určeníprůsečnice stačí nalézt dva z těchto stopníků.Příklad 7.8 Sestrojíme průsečnici rovin ρ a σ, určených stopami - obr. 7.23.Řešení: (obr. 7.24)1. Průsečík nárysných stop n ρ a n σ je nárysný stopník N hledané průsečnice. Jeho půdorysN 1 leží na ose x.2. Průsečík bokorysných stop m ρ a m σ je bokorysný stopník M hledané průsečnice. Jehopůdorys M 1 leží na ose y.3. Spojnice bodů N a M je průsečnice rovin ρ a σ.4. Půdorysný stopník P je průsečíkem půdorysných stop a také leží na sestrojené průsečnici.□□

7.6. Úlohy v axonometrii 78Obrázek 7.23: Obrázek 7.24:7.6.5 Kružnice v souřadnicové roviněObrazem kružnice v axonometrii je elipsa, protože se jedná o rovnoběžné promítání. Průměrykružnice, které jsou rovnoběžné s osami ležícími v rovině kružnice se zobrazí do sdruženýchprůměrů elipsy. Hlavní osy elipsy získáme pomocí Rytzovy konstrukce.Obrázek 7.25: Obrázek 7.26:Příklad 7.9 Sestrojíme kružnici se středem v bodě S a poloměrem 3 jednotky ležící v roviněyz - obr. 7.25.Řešení: (obr. 7.26)1. Bodem S vedeme rovnoběžku s osou y a naneseme na ni na obě strany třikrát jednotkuj y . Získané body označíme A, B.2. Bodem S vedeme rovnoběžku s osou z a naneseme na ni na obě strany třikrát jednotkuj z . Získané body označíme C, D.3. Úsečky AB a CD jsou sdružené průměry elipsy, do které se zobrazí kružnice v rovině yz.4. Hlavní osy sestrojíme pomocí Rytzovy konstrukce.□

7.7. Pravoúhlá axonometrie 797.7 Pravoúhlá axonometriePůdorysnu, nárysnu a bokorysnu protneme rovinou α, která neprochází počátkem a protínávšechny tři osy - obr. 7.27. Průsečíky roviny α s osami označíme X, Y, Z. Trojúhelník XY Zje vždy ostroúhlý. Rovina α je axonometrickou průmětnou, do které budeme pravoúhlepromítat. Trojúhelníku XY Z říkáme axonometrický trojúhelník. Tento trojúhelník se zobrazojevždy ve skutečné velikosti, nebot’ leží v axonometrické průmětně.Obrázek 7.27: Obrázek 7.28:Podívejme se, jak se zobrazí v pravoúhlé axonometrii osy x, y, z. Osa z je kolmá k roviněxy, a tudíž ke všem přímkám této roviny, tedy i k přímce XY . Přímka XY leží v axonometricképrůmětně. Podle věty 5.1 o pravoúhlém průmětu pravého úhlu se osa z a přímka XY zobrazíjako kolmice. Stejné závěry můžeme udělat i o ose y a přímce XZ a ose x a přímce Y Z. Můžemeproto vyslovit následující větu:Věta 7.2 Osy x, y, z se promítnou do výšek axonometrického trojúhelníka - obr. 7.28.Je-li dán axonometrický trojúhelník, umíme sestrojit axonometrické průměty os. Obráceně:jsou-li dány průměty os (axonometrický osový kříž), můžeme sestrojit nekonečně mnoho axonometrickýchtrojúhelníků, které jsou navzájem podobné. Volbou axonometrického trojúhelníkavolíme axonometrickou průmětnu dál nebo blíž od počátku. Volba axonometrického trojúhelníka,a tím i axonometrické průmětny, nemá vliv na velikost a tvar průmětů, protože všechny tytoroviny jsou navzájem rovnoběžné.Pravoúhlá axonometrie je speciálním případem axonometrie obecné, proto řešíme polohovéúlohy stejně jako v obecné axonometrii. Navíc si ukážeme řešení rovinných úloh v půdorysně,nárysně a bokorysně.7.7.1 Metrické úlohy v rovinách xy, yz, zxRovinné úlohy v rovinách xy, yz a zx řešíme pomocí otočení příslušné roviny do axonometricképrůmětny. Osou otáčení je jedna z přímek XY , Y Z, ZX. Do axonometrické průmětny vždynejprve otočíme počátek. Mezi axonometrickými průměty bodů a jejich otočenými průměty

7.7. Pravoúhlá axonometrie 80opět existuje afinita, další body tedy získáme pomocí afinity. V otočení vyřešíme rovinnou úlohu(najdeme velikosti jednotek na osách, sestrojíme podstavu tělesa atd.) a výsledek otočíme zpětdo axonometrické průmětny.Pro určení obecné axonometrie jsme museli zadat axonometrický osový kříž s velikostmijednotek na jednotlivých osách. Tím byla obecná axonometrie podle Pohlkeovy věty 7.1 jednoznačněurčena. V pravoúhlé axonometrii máme zadán směr promítání a umíme určit jednotkyna osách,což si ukážeme v následujícím příkladu.Obrázek 7.29: Obrázek 7.30:Příklad 7.10 Je dán axonometrický trojúhelník XY Z. Sestrojíme průměty os x, y, z a jednotkyna osách - obr. 7.29.Řešení: (obr. 7.30)1. Osy x, y, z se promítnou do výšek axonometrického trojúhelníka XY Z.2. Otočíme rovinu xy kolem přímky XY . Otáčíme bod O: rovina otáčení je kolmá k přímceXY a prochází bodem O, promítne se do přímky k. Nemusíme hledat střed a poloměrotáčení, protože víme, že přímky x a y jsou ve skutečnosti kolmé a musí po otočení přejítdo kolmic. Otočený bod O leží na přímce k a na Thaletově kružnici sestrojené nad úsečkouXY , označíme ho (O).3. Otočená přímka x (označíme ji (x)) prochází bodem (O) a bodem X, který při otáčenízůstává na místě, protože leží na ose otáčení.4. Otočená přímka y (označíme ji (y)) prochází bodem (O) a bodem Y , který při otáčenízůstává na místě, protože leží na ose otáčení.5. Na otočených osách vyznačíme jednotky ve skutečné velikosti.6. Pomocí afinity s osou XY a párem odpovídajících si bodů O, (O) odvodíme jednotky naosy x a y.7. Pomocí otočení roviny yz kolem přímky Y Z získáme stejným způsobem jednotky na osez (a znovu na ose y).8. Není třeba otáčet rovinu xz, protože bychom jen znovu získali jednotky na osách x a z.

7.7. Pravoúhlá axonometrie 81Obrázek 7.31: Obrázek 7.32:Příklad 7.11 V pravoúhlé axonometrii určené osovým křížem sestrojíme obraz čtverce ABCD,který leží v rovině yz, je-li dána úhlopříčka AC. - obr. 7.31.Řešení: (obr. 7.32)1. Sestrojíme axonometrický trojúhelník XY Z. Strany trojúhelníka jsou kolmé na osy x, y az. Stranu Y Z volíme tak, aby procházela bodem A (zjednodušíme si tím další konstrukci).2. Pomocí Thaletovy kružnice a kolmice bodem O k přímce Y Z otočíme bod O - otočenýbod označíme O 0 .3. S použitím afinity s osou Y Z a párem odpovídajících si bodů O, O 0 otočíme body A aC (bod A je samodružný, protože jsme přímku Y Z, neboli osu otáčení, zvolili bodem A.Otočené body označíme A 0 a C 0 .4. V otočení sestrojíme čtverec A 0 B 0 C 0 D 0 .5. Pomocí afinity otočíme čtverec zpět a získáme axonometrický obraz čtverce ABCDležícího v rovině yz□Podobně můžeme sestrojovat rovinné útvary v rovinách xy a xz.□7.7.2 Obraz kružnice ležící v některé souřadnicové roviněKružnici v půdorysně, nárysně nebo bokorysně můžeme sestrojit stejně jako v příkladu 7.9.V pravoúhlé axonometrii si však můžeme tuto úlohu zjednodušit. V pravoúhlém promítání seúsečky rovnoběžné s průmětnou zobrazí ve skutečné velikosti a všechny ostatní se promítnutímzkrátí. To znamená, že velikosti stran axonometrického trojúhelníka a všech úseček s nimirovnoběžných se zobrazí ve skutečné velikosti. Průměr kružnice k ležící v rovině xy rovnoběžnýs úsečkou XY se promítne do hlavní osy elipsy, do které se zobrazí kružnice k. Podobně hlavníosa elipsy, do které se zobrazí kružnice ležící v rovině yz, je rovnoběžná s úsečkou Y Z a rovna

7.7. Pravoúhlá axonometrie 82skutečnému poloměru kružnice. Hlavní osa elipsy, do které se zobrazí kružnice ležící v rovinězx, je rovnoběžná s úsečkou ZX a rovna skutečnému poloměru kružnice.Protože pravoúhlé promítání zachovává rovnoběžnost, můžeme najít další bod kružnice narovnoběžkách vedenými hlavními vrcholy elipsy s osami ležícími v rovině kružnice.Obrázek 7.33: Obrázek 7.34:Příklad 7.12 V pravoúhlé axonometrii určené axonometrickým trojúhelníkem sestrojte kružnicim(V ; r 1 ) ležící v rovině xy a kružnici n(U; r 2 ) ležící v rovině yz - obr. 7.33.Řešení: (obr. 7.34)1. Sestrojíme osy x, y, z jako výšky axonometrického trojúhelníka XY Z.2. Bodem V vedeme rovnoběžku s přímkou XY a naneseme na ni na obě strany velikost r 1 .Body označíme A a B, jsou to hlavní vrcholy elipsy m.3. Bodem A vedeme rovnoběžku s osou x a bodem B rovnoběžku s osou y, jejich průsečíkje bod M. Bod M je bodem elipsy. Nyní můžeme pomocí proužkové konstrukce (není vobrázku vyznačena) sestrojit vedlejší osu hledané elipsy a tedy i celou elipsu m.4. Elipsa m je obrazem hledané kružnice m(V ; r 1 ).5. Podobně sestrojíme obraz kružnice n(U; r 2 ) v rovině yz: hlavní osa CD elipsy je rovnoběžnás přímkou Y Z a její velikost je rovna poloměru r 2 . Bod N je průsečíkem rovnoběžekvedených body C a D s osami z a y. K sestrojení elipsy použijeme opět proužkovoukonstrukci.Stejně bychom setrojili i kružnici v rovině xz a kružnice v rovinách rovnoběžných s rovinamixy, yz a xz.□Nyní umíme sestrojit rovinný útvar v půdorysně, nárysně a bokorysně. To znamená, žeumíme sestrojit základní tělesa jako hranoly, válce, kužele a jehlany s podstavou v těchtorovinách. V další kapitole se ještě naučíme řešit průniky těchto těles s přímkami a rovinami.

7.8. KontrolnÍ otázky 837.8 Kontrolní otázky7.1 Uved’te, čím je obecně určena axonometrie.7.2 Uved’te dva základní způsoby určení pravoúhlé axonometrie a popište vzájemný vztahmezi určujícími prvky v prvním a druhém způsobu určení.7.3 Jakou konstrukci elipsy využijete při zobrazení kružnice v pravoúhlé, resp. obecné axonometrii?

Literatura[1] Bohne, E. – Klix, W.D.: Geometrie – Grundlagen für Anwendungen. Leipzig, Fachbuchverlag1995.[2] Polák, J.: Přehled středoškolské matematiky. Praha, SPN 1991.[3] Rogers, D.F. – Adams, J.A.: Mathematical Elements for Computer Graphics. New York,Mc Graw–Hill 1990.[4][5]Štauberová, Z.: Mongeovo promítání. Plzeň, ZČU 2004.Štauberová, Z.: Axonometrie, křivky, plochy. Plzeň, ZČU 2004. 1997.[6] Urban, A.: Deskriptivní geometrie I. Praha, SNTL 1965.[7] Kriegelstein, E.– Kriegelstein, M.: Deskriptivní geometrie 1, 2. Praha, 1988.[8] Drs, L.: Deskriptivní geometrie 1, 2. Praha, 1988.84