x f(x) f'(x) - +

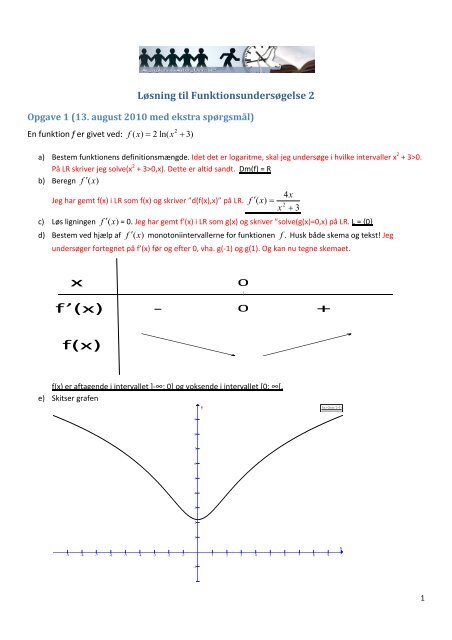
Løsning til Funktionsundersøgelse 2
Opgave 1 (13. august 2010 med ekstra spørgsmål)
En funktion f er givet ved:
f x
2
( ) = 2ln( x + 3)
a) Bestem funktionens definitionsmængde. Idet det er logaritme, skal jeg undersøge i hvilke intervaller x 2 + 3>0.
På LR skriver jeg solve(x 2 + 3>0,x). Dette er altid sandt. Dm(f) = R
b) Beregn f ′(x)
4x
Jeg har gemt f(x) i LR som f(x) og skriver ”d(f(x),x)” på LR. f ′( x)
=
x
2 + 3
c) Løs ligningen f ′(x)
= 0. Jeg har gemt f’(x) i LR som g(x) og skriver ”solve(g(x)=0,x) på LR. L = {0}
d) Bestem ved hjælp af f ′(x)
monotoniintervallerne for funktionen f . Husk både skema og tekst! Jeg
undersøger fortegnet på f’(x) før og efter 0, vha. g(‐1) og g(1). Og kan nu tegne skemaet.
x
f’(x)
0
‐ 0 +
f(x)
f(x) er aftagende i intervallet ]‐∞; 0] og voksende i intervallet [0; ∞[.
e) Skitser grafen
y
f(x)=2ln(x^2+3)
9
8
7
6
5
4
3
2
1
x
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-1
1

f) Bestem en ligning for tangenten grafen for f i punktet P(0 , f (0)). Jeg finder først funktionsværdien:
f(0) =2ln(3). Derefter hældningskoefficienten til tangenten. f’(0) = g(0) = 0. Tangentens ligning bliver:
y = f ′ x )( x − x ) + f ( x )
y = 0( x − 0) + 2ln(3)
y = 2ln(3)
(
0 0
0
g) Løs ved beregning ligningen f′ ( x) = 1. Denne løses ved hjælp af LR, jeg skriver solve(g(x) = 1,x). L = {1; 3}
Opgave 2 (13. august 2010 med ekstra spørgsmål)
1 4 3 5 2
En funktion f er givet ved: f ( x) = x − 2x + x
4 2
a) Bestem definitionsmængden for funktionen f. Dm(f) = R
b) Bestem nulpunkterne for funktionen f. (dvs. løs ligningen f(x) = 0 og angiv skæring med y‐aksen)
Jeg gemmer funktionen i f(x) på LR, og skriver: ”solve(f(x)=0,x). Jeg kan nu opskrive punkterne hvor f(x) skær
x‐aksen: ( 4 6;0 );
( 4 − 6;0 );
( 0;0)
c) Beregn f ′(x)
+ . Skæring med y‐aksen er i f(0) = 0, så det er også punktet (0, 0).
3 2
Jeg har gemt f(x) i LR og skriver ”d(f(x),x)” på LR. f ′(
x)
= x − 6x
+ 5x
d) Løs ligningen f ′(x)
= 0 Jeg har gemt f’(x) i LR som g(x) og skriver ”solve(g(x)=0,x) på LR. L = {0; 1; 5}
Tegn monotoniskemaet og beskriv ved hjælp heraf funktionens monotoniintervaller. Jeg undersøger
fortegnet på f’(x) før og efter 0, efter 1 og efter 5 vha. g(‐1), g(½), g(2) og g(6). Og kan nu tegne skemaet.
x
0
1
5
f’(x)
f(x)
‐ 0 + 0 ‐ 0
+
f(x) er aftagende i intervallerne ]‐∞; 0]og [1; 5]; og f(x) er voksende i intervallerne [0; 1]og [5; ∞[.
e) Bestem koordinaterne til de punkter på funktionens graf, hvor grafen har lokale ekstremumspunkter.
Jeg har x‐koordinaterne, så jeg skal have fundet y‐koordinaterne: f(0) = 0, f(1) = ¾ og f(5) = ‐125/4.
⎛ 125 ⎞
Funktionen har lokalt minimumspunkt i (0, 0) og globalt minimumspunkt i ⎜5
; − ⎟
⎝ 4 ⎠
⎛ 3 ⎞
Funktionen har lokalt maksimumspunkt i ⎜1
; ⎟
⎝ 4 ⎠
2

f) Skitser grafen for f og bestem funktionens værdimængde.
y
f(x)=x^4/4-2x^3+5/2*x^2
5
x
-4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-5
-10
-15
-20
-25
-30
⎡ 125 ⎡
Vm ( f ) = ⎢−
; ∞
⎣ 4 ⎢
⎣
h) Bestem en ligning for tangenten til funktionens graf i punktet P = (2, − 2) . Jeg finder først funktionsværdien:
f(2) =‐2. Derefter hældningskoefficienten til tangenten. f’(2) = g(2) = ‐6. Tangentens ligning bliver:
y = f ′ x )( x − x ) + f ( x )
(
0 0
0
y = 6( x − 2) − 2
y = −6x
+ 10
Jeg kan også skrive på LR: y = g(2)*(x‐2)+f(2). Dette giver y = 10‐6x. Dette skal jeg omskrive, så det er som
ovenstående.
Opgave 3 (16. december 2010)
8
En funktion f er givet ved: f ( x)
= 1−
x
2 − 2x
a) Bestem funktionens definitionsmængde og skitser funktionens graf. For at finde
Dm(f) undersøger jeg, hvornår nævneren bliver 0, dette gøres på LR: ”solve(x 2 ‐2x =
0,x). Dm(f) = R\{0; 2}
3

y
f(x)=1-8/(x^2-2x)
x=2
15
10
5
x
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
-5
-10
-15
b) Bestem nulpunkterne for funktionen. Jeg gemmer funktionen i f(x) på LR, og skriver:
”solve(f(x)=0,x). Jeg kan nu opskrive punkterne hvor f(x) skærer x‐aksen: (‐2; 0) og (4; 0).
Skæring med y‐aksen er i f(0) = undef, så der er ingen skæring med y‐aksen.
c) Bestem funktionens monotoniintervaller, samt koordinaterne til de punkter på
funktionens graf, hvor der er lokale ekstremumspunkter. Jeg skal først
differentierer funktionen, dette gør jeg på LR. Jeg skriver ”d(f(x),x)” og får
16( x −1)
f ′(
x)
= Denne gemmes i g(x) på LR. Derefter løser jeg ligningen: f’(x) =
2 2
x ( x − 2)
0, også på LR: ”solve(g(x)=0,x)”. Dette giver løsningen x=1. Så undersøger jeg
fortegnet på f’(x) før 1 og efter 1 og husker jeg har to x‐værdier hvor funktionen
ikke er defineret x=0 og x=2: g(½) og g(3/2). Derefter undersøger jeg fortegnet før 0
og efter 2. g(‐1) og g(3).
x
0 1 2
f’(x)
‐ i d 0
‐ +
i d
+
f(x)
f(x) er aftagende i intervallerne ]‐∞; 0[og ]0; 1]; og f(x) er voksende i intervallerne
[1; 2[og ]2; ∞[. Jeg har x‐værdien til minimumspunktet, så jeg skal finde y: f(1) =9.
Funktionen har lokalt minimumspunkt i (1, 9)
d) Bestem for x < 0 ligningen for den tangent til funktionens graf, der er parallel med
3
linjen med ligningen y = − x + 1 . Jeg aflæser hældningskoefficienten til tangenten
4
til ‐3/4. Jeg løser nu ligningen f’(x) = ‐3/4. På LR skriver jeg ”solve(g(x)=‐3/4,x)”.
Dette giver x = ‐2 og x = 0,95. Men jeg skal kun finde en tangent for x

hældningskoefficienten til tangenten. f’(‐2) = ‐3/4. Tangentens ligning bliver:
y = f ′( x0
)( x − x0
) + f ( x0
)
3
y = − ( x − ( −2))
− 0
4
3 3
y = − x −
4 2
Opgave 4 (16. december 2010)
En funktion f er givet ved
f ( x)
= 3e
−2x
Beregn en ligning for den linje l, der indeholder punktet P (−1,5)
og er parallel med tangenten til grafen for f i
punktet Q( 0, f (0)).
Jeg gemmer først funktionen i f(x). Derefter differentierer jeg funktionen for at finde hældningskoefficienten til
−2x
tangenten. jeg skriver ”d(f(x),x)” f ′(
x)
= −6e
Denne gemmes i g(x). derefter finder jeg hældningskoefficienten til
y = a( x − x1)
+ y1
tangenten g(0). f’(0) = ‐6. Jeg kan nu finde linjens ligning: y = −6(
x − ( −1))
+ 5
y = −6x
−1
8
y
f(x)=3*e^(-2x)
y=-6x+3
f(x)=-6x-1
6
4
2
x
-4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5
-2
-4
-6
-8
5