Kapitel 3 - Mathematik

Skript zu Komplexe Zahlen M. Ludwig
3 Geometrische Deutung der komplexen Zahlen
3.1 Die Ebene der komplexen Zahlen
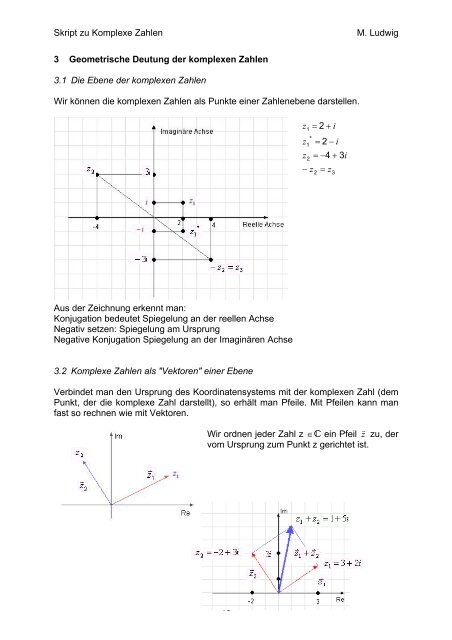
Wir können die komplexen Zahlen als Punkte einer Zahlenebene darstellen.
Aus der Zeichnung erkennt man:
Konjugation bedeutet Spiegelung an der reellen Achse
Negativ setzen: Spiegelung am Ursprung
Negative Konjugation Spiegelung an der Imaginären Achse
3.2 Komplexe Zahlen als "Vektoren" einer Ebene
Verbindet man den Ursprung des Koordinatensystems mit der komplexen Zahl (dem
Punkt, der die komplexe Zahl darstellt), so erhält man Pfeile. Mit Pfeilen kann man
fast so rechnen wie mit Vektoren.
Wir ordnen jeder Zahl z ∈C ein Pfeil z zu, der
vom Ursprung zum Punkt z gerichtet ist.
- 13 -
z
z
z
1
*
1
2
− z
= 2 + i
= 2 − i
= −4
+ 3i
2
= z
3

Skript zu Komplexe Zahlen M. Ludwig
3.3 Beträge komplexer Zahlen
Obwohl C kein angeordneter Körper ist, kann man durch eine eindeutige Abbildung
komplexe Zahlen in eine gewisse Anordnung bringen.
B: C → R + (Pseudoskalarprodukt)
B: z z
Die Länge des Pfeils/Vektors nennen wir Betrag von z.
z = x + iy =
2
x
2
+ y =
*
z ⋅ z
z ist auch der Abstand von z zum Ursprung.
⇒ ∃ unendlich viele z ∈C mit dem gleichen Abstand vom Ursprung. Sie liegen alle
K z ; 0,
0
( )
auf dem Kreis ( )
Anwendung des Betrags bei der Dreiecksungleichung.
Satz: z 1 + z 2 ≤ z1
+ z 2
ϕ z 1 + z2
2 2
= z1
+ z2
2
+ 2 z1
z2
cos (Cosinussatz)
≤1
z
+ z
1
z + z ≤ z +
1
( z + z )
z1
+ z2
≤ 1 2
> 0
2
2
2
≤ z
2
1
2
- 14 -
+
> 0
z
1
2
2
2
+ 2 z
z
2
1
z
2
q.
e.
d.

Skript zu Komplexe Zahlen M. Ludwig
3.4 Deutung der Multiplikation
3.4.1 Polarform der komplexen Zahlen
Man kann die komplexen Zahlen auch in einer anderen Form schreiben. Man nutzt
dazu die Polarkoordinaten.
ϕ = arg( z)
0 ≤ arg( z)
= ϕ < 2π
⇒ Es gibt also eine eindeutige Abbildung P (Polarkoordinaten) von C nach R× W
(W = Menge der Winkel zwischen 0 und 2π ).
P: C R × W
⎛ 2 2 −1⎛
y ⎞⎞
P: x + iy ⎜ x + y ; tan ⎜ ⎟⎟
⎝
⎝ x ⎠⎠
Da die Winkel zwischen 0 und 2π liegen, gibt es auch eine eindeutige
Umkehrabbildung.
P 1 − : R × W C
P 1
z ; ϕ z cosϕ
+ z i sin
− : ( ) ϕ
z [ cosϕ + i sinϕ
]
Für cosϕ + i sinϕ
schreibt man auch E(ϕ ).
⇒ z = z ⋅ E(
ϕ )
x = z cosϕ
= Re( z)
y = z sinϕ
= Im( z)
z
=
Im( z)
tanϕ
= =
Re( z)
Da P und P -1 eindeutige Abbildungen sind, nennt man P auch eineindeutig oder
bijektiv. Man kann also ohne „Verluste“ hin- und herrechnen.
- 15 -
x
2
+ y
2
=
y
x
z ⋅ z
*
⇒ tan
−1
⎛ y ⎞
⎜ ⎟ = ϕ
⎝ x ⎠

Skript zu Komplexe Zahlen M. Ludwig
Umrechnung:
Beispiele:
1)
2)
z = 2i
π
z = 2 ϕ =
2
⎛π
⎞
⇒ z = 2E⎜
⎟
⎝ 2 ⎠
z = 3 − 2i
z
=
ϕ = tan
ϕ ≈ 326,
3
ϕ ≈1,
813π
z ≈
Kleines Glossar
9 + 4 =
−1
⎛ − 2 ⎞
⎜ ⎟
⎝ 3 ⎠
13
13E(
1,
813π
)
Umrechnung von ϕ in RAD nach DEG
ϕ (RAD) → ϕ (DEG)
Name Bedeutung Schreibweise
Betrag von z Länge r von z z
Argument von z Winkel ϕ von z arg (z)
Realteil von z X – Koordinate Re(z)
Imaginärteil von z Y – Koordinate Im(z)
imaginäre Zahl Reelles Vielfaches von i
reelle Achse R
imaginäre Achse i R
Konjugiert
Komplexe Zahl von z
°
360
180
ϕ °
⋅180
π
ϕ ( RAD )
ϕ ( DEG ) = ⋅180
°
π
α
°
°
= ˆ 2π
= ˆ π
DEG = ˆ RAD
von
Umrechnen
DEG
von
nach
Spiegelung von
z an der reellen Achse
- 16 -
RAD
α ( DEG )
α ( RAD ) = ⋅ π °
180
z oder z
*

Skript zu Komplexe Zahlen M. Ludwig
3.4.2 Eigenschaften von E(ϕ )
a) Allgemeines
E
⇒
E
( ϕ ) = cosϕ
+ i sinϕ
E(
ϕ ) ∈
( ϕ + 2π
) = E(
ϕ + k ⋅ 2π
) = E(
ϕ )
E( ϕ ) ist 2π -periodisch (k ∈Z)
E 0 = E 2π
=
( ) ( ) 1
( ϕ ) = 1 ∀ϕ
∈
E R
2
2
2
2
Beweis: cos ϕ + sin ϕ = 1 (ausführlicher | E ( ϕ)
| = cos ϕ + sin ϕ = 1)
b) Das Produkt
i ⋅i = −1
2i ⋅ 2i
= −4
− 1 ⋅ ( −1)
= 1
1
(
2
2
2(
1+
i )) = i
( ϕ ) ⋅ E(
ϕ ) = ( cosϕ + i sinϕ
)( cosϕ
i sinϕ
)
E 1 2
1
1 2 + 2
= cosϕ
cosϕ
+ i sinϕ
cosϕ
+ i sinϕ
cosϕ
− sinϕ
sinϕ
1
2
= cosϕ
2 cosϕ
1 − sinϕ
1 sinϕ
2 + i
=
cos
( ϕ ) E(
ϕ ) = E(
ϕ + ϕ ) ∀ ∈
E 1 ⋅ 2
1 2 , ϕ1
/ 2 R
- 17 -
( sinϕ
cosϕ
+ sinϕ
cosϕ
)
( ϕ + ϕ ) + i sin(
ϕ + ϕ )
1
2
2
1
1
2 1
1 2
Multiplikation bedeutet also Addition der Argumente und Multiplikation der Beträge.
⇒ z ⋅ z = z E ϕ ) ⋅ z ⋅ E(
ϕ ) = z ⋅ z ⋅ E(
ϕ + ϕ )
1
2
1
( 1 2 2 1 2 1 2
1
2
2
1
2

Skript zu Komplexe Zahlen M. Ludwig
c) Spezialfälle
E( ϕ ) ⋅ E(
− ϕ ) = E(
0)
= 1
n ( E(
ϕ ) ) = E(
ϕ ) ⋅ ⋅ E(
ϕ ) = E(
nϕ
)
…
n−
fach
Das erinnert alles ein wenig an das Rechnen mit der Exponentialfunktion.
⇒ Es gilt:
!
!
iϕ
( ϕ ) e = cosϕ
+ i sinϕ
E = Eulersche Formel
Daraus folgt sofort für j = p der Topsatz unter den Top Ten der schönsten
mathematischen Sätze.
iπ
oder e + 1 = 0
Grundlegende Erklärung für die Eulersche Formel:
2 3
x x
e = 1 + x + + + …
2!
3!
x
Potenzreihenentwicklung der Exponentialfunktion
2
3
4
ϕ ( iϕ
) ( iϕ
) ( iϕ)
e = 1 + iϕ
+ + + + …
2!
3!
4!
i
2 4 6
3 5
ϕ ϕ ϕ ⎛ ϕ ϕ ⎞
= 1 − + − … + i ⎜
⎜ϕ
− + … ⎟
2! 4!
6
! ⎝ 3!
5!
⎠
C
S
'
'
iπ
e
= C
= −1
( ϕ ) + iS(
ϕ )
( ϕ ) = −S(
ϕ )
3 5
ϕ ϕ
= −ϕ
+ − + …
3! 6!
2
ϕ
4
ϕ
2!
4!
( ϕ ) = C(
ϕ ) = 1 − + + …
zu zeigen: e = const = 1
iϕ
2
d e
iϕ
dϕ
=
=
( ) '
2 2
C + S
' '
( 2CC
+ 2SS
)
= 2
( − CS + CS )
= 0
⇒ Der Betrag ändert sich nicht!
⇒ e const!
q.
e.
d.
i ϕ
=
denn wir wissen, dass cos ϕ + i sinϕ
= 1
Ableitung des Betragsquadrates
- 18 -