SCARA: Inverses Kinematisches Problem - BA-Produktionstechnik.de
SCARA: Inverses Kinematisches Problem - BA-Produktionstechnik.de
SCARA: Inverses Kinematisches Problem - BA-Produktionstechnik.de
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
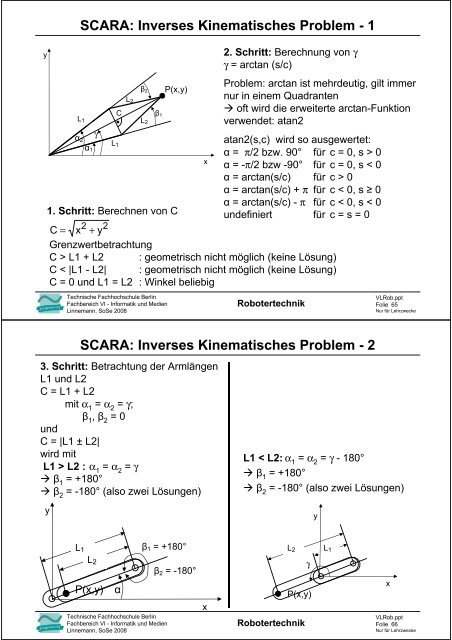
y<br />
<strong>SCARA</strong>: <strong>Inverses</strong> <strong>Kinematisches</strong> <strong>Problem</strong> - 1<br />
L 1<br />
α 2<br />
α 1<br />
γ<br />
L 1<br />
C<br />
L 2<br />
β 2<br />
L 2<br />
β 1<br />
P(x,y)<br />
1. Schritt: Berechnen von C<br />
2 2<br />
C = x + y<br />
Grenzwertbetrachtung<br />
C > L1 + L2 : geometrisch nicht möglich (keine Lösung)<br />
C < |L1 - L2| : geometrisch nicht möglich (keine Lösung)<br />
C = 0 und L1 = L2 : Winkel beliebig<br />
x<br />
2. Schritt: Berechnung von γ<br />
γ = arctan (s/c)<br />
<strong>Problem</strong>: arctan ist mehr<strong>de</strong>utig, gilt immer<br />
nur in einem Quadranten<br />
oft wird die erweiterte arctan-Funktion<br />
verwen<strong>de</strong>t: atan2<br />
atan2(s,c) wird so ausgewertet:<br />
α = π/2 bzw. 90° für c = 0, s > 0<br />
α = -π/2 bzw -90° für c = 0, s < 0<br />
α = arctan(s/c) für c > 0<br />
α = arctan(s/c) + π für c < 0, s ≥ 0<br />
α = arctan(s/c) - π für c < 0, s < 0<br />
un<strong>de</strong>finiert für c = s = 0<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 65<br />
Nur für Lehrzwecke<br />
<strong>SCARA</strong>: <strong>Inverses</strong> <strong>Kinematisches</strong> <strong>Problem</strong> - 2<br />
3. Schritt: Betrachtung <strong>de</strong>r Armlängen<br />
L1 und L2<br />
C = L1 + L2<br />
mit α 1<br />
= α 2<br />
= γ;<br />
β 1<br />
, β 2<br />
= 0<br />
und<br />
C = |L1 ± L2|<br />
wird mit<br />
L1 > L2 : α 1<br />
= α 2<br />
= γ<br />
β 1<br />
= +180°<br />
β 2<br />
= -180° (also zwei Lösungen)<br />
L1 < L2: α 1<br />
= α 2<br />
= γ - 180°<br />
β 1<br />
= +180°<br />
β 2<br />
= -180° (also zwei Lösungen)<br />
y<br />
y<br />
L 1 β 1 = +180°<br />
L 2<br />
L 1<br />
L 2<br />
P(x,y)<br />
α<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
β 2 = -180°<br />
x<br />
γ<br />
P(x,y)<br />
Robotertechnik<br />
x<br />
VLRob.ppt<br />
Folie 66<br />
Nur für Lehrzwecke
<strong>SCARA</strong>: <strong>Inverses</strong> <strong>Kinematisches</strong> <strong>Problem</strong> - 3<br />
4. Schritt:<br />
Der „Normalfall“: β 1<br />
und β 2<br />
berechnen<br />
Es ist<br />
C < L 1<br />
+ L 2<br />
(keine gestreckten Arme)<br />
und<br />
C > |L 1<br />
–L 2<br />
| (Arme nicht „gefaltet“)<br />
womit gilt:<br />
y<br />
y p<br />
L 1<br />
α 2<br />
α 1<br />
γ<br />
L 1<br />
C<br />
L 2<br />
β 2<br />
L 2<br />
β 1<br />
x p<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
P(x,y)<br />
x<br />
Für das untere schiefwinklige Dreick gilt:<br />
x p2<br />
+ y p2<br />
= C 2 = L 12<br />
+ L 22<br />
+ 2L 1<br />
L 2<br />
cos β 1<br />
(Cosinussatz)<br />
Für das obere schiefwinklige Dreieck gilt<br />
x p2<br />
+ y p2<br />
= C 2 = L 12<br />
+ L 22<br />
+ 2L 1<br />
L 2<br />
cos β 2<br />
(Cosinussatz)<br />
und es ist auch<br />
β1 > 0<br />
β2 < 0<br />
(aber bei<strong>de</strong> haben <strong>de</strong>n gleichen Betrag!)<br />
und man kann die Gleichungen<br />
gleichsetzen:<br />
x p2<br />
+ y p2<br />
= C 2 = L 12<br />
+ L 22<br />
+ 2L 1<br />
L 2<br />
cos β 1<br />
= L 12<br />
+ L 22<br />
+ 2L 1<br />
L 2<br />
cos β 2<br />
Robotertechnik<br />
2 2<br />
( L L )<br />
⎛ 2 2<br />
⎜ x + y − +<br />
β = ±<br />
1<br />
1 arccos<br />
⎜ 2 L<br />
⎝<br />
1L2<br />
2<br />
⎞<br />
⎟<br />
⎟<br />
⎠<br />
VLRob.ppt<br />
Folie 67<br />
Nur für Lehrzwecke<br />
<strong>SCARA</strong>: <strong>Inverses</strong> <strong>Kinematisches</strong> <strong>Problem</strong> - 4<br />
y<br />
5. Schritt: α 1<br />
und α 2<br />
berechnen<br />
L 1<br />
α 2<br />
α 1<br />
γ<br />
C<br />
δ<br />
-δ<br />
L 1<br />
L 2<br />
L 2<br />
P(x,y)<br />
α 1<br />
= γ - δ<br />
α 2<br />
= γ + δ<br />
Mit <strong>de</strong>m Cosinussatz wird<br />
L 2 2 = L 1 2 + C 2 –2 CL 1<br />
cos δ<br />
⎛ 2 2 2 ⎞<br />
⎜L<br />
− L + C<br />
δ = arccos 1 2 ⎟<br />
⎜ 2 L C ⎟<br />
⎝<br />
1<br />
⎠<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
x<br />
Fazit:<br />
Der Weg <strong>de</strong>r „traditionellen Geometrie“ führt<br />
zum Ziel, ist aber<br />
• Recht aufwändig abzuleiten<br />
• Nicht übertragbar auf an<strong>de</strong>re<br />
Kinematiken<br />
• Führt bei komplexen Kinematiken<br />
zu umfangreichen „Kunstwerken“<br />
Bei mehr<strong>de</strong>utigen Lösungen besteht bei <strong>de</strong>r<br />
inversen Kinematik das <strong>Problem</strong>, welche <strong>de</strong>r<br />
Lösungen man in <strong>de</strong>r Steuerung auswählt:<br />
• Programmierer <strong>de</strong>s Anwendungsproblems<br />
wählt aus.<br />
• Vorherige Stellung als Entscheidungskriterium,<br />
z.B. die Winkel, die am<br />
nächsten liegen nehmen.<br />
• Hin<strong>de</strong>rnisse erkennen Den Fall <strong>de</strong>r<br />
Kollisionsvermeidung nehmen.<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 68<br />
Nur für Lehrzwecke
Übung: K‘-transformation mit konventioneller Geometrie<br />
z<br />
Aufgabe mit einfach zur<br />
rechnen<strong>de</strong>n dimensionslosen<br />
Zahlenwerten:<br />
Gelenk 2<br />
(Rotation)<br />
P(x p , y p , z p )<br />
y<br />
Gelenk 1<br />
(Translation)<br />
z p<br />
y p<br />
α<br />
d 3<br />
Gelenk 3<br />
(Translation)<br />
a) Direktes <strong>Problem</strong><br />
Gegeben:<br />
d 1 = 3, d 3 = 4, α = 30°<br />
Gesucht: Position von P<br />
Lösung:<br />
x P = 3,464<br />
y P = 2,0<br />
z P = 3<br />
b) <strong>Inverses</strong> <strong>Problem</strong>:<br />
Gegeben:<br />
x P , y P , z P , Werte wie a)<br />
Gesucht: d 1 , d 3 , α<br />
Lösung: siehe a)<br />
d 1<br />
x p<br />
x<br />
Festpunkt<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 69<br />
Nur für Lehrzwecke<br />
Aus drucktechnischen Grün<strong>de</strong>n leere Folie!<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 70<br />
Nur für Lehrzwecke
5. Koordinatentransformation<br />
• Grundlagen<br />
• Position und Orientierung eines Körpers im Raum<br />
• Rotationen<br />
• Homogene Koordinaten und Transformationen<br />
• Denavit-Hartenberg-Verfahren (direktes kinemat. <strong>Problem</strong>)<br />
• Beschreibung nach DH<br />
• Bezeichnungen nach DH<br />
• DH-Transformation für Translation und Rotation<br />
• Bestimmung <strong>de</strong>r DH-Parameter<br />
• Anwendung von DH auf Industrieroboter<br />
• DH am Beispiel eines <strong>SCARA</strong>-Roboters<br />
• Übungsaufgaben<br />
• <strong>Inverses</strong> kinematisches <strong>Problem</strong><br />
• Analytisches Verfahren von Paul<br />
• Numerische Verfahren<br />
• Beispiel: <strong>SCARA</strong><br />
• Übungsaufgaben<br />
• Singularitäten<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 71<br />
Nur für Lehrzwecke<br />
Position und Orientierung eines Körpers im Raum<br />
e<br />
p<br />
e = Einheitsvektoren<br />
e yK zK<br />
K<br />
e xK<br />
d K Es wird unterschie<strong>de</strong>n:<br />
• Bezugskoordinatensystem (base frame);<br />
fixiert, ortsfest,<br />
z.B. am Bo<strong>de</strong>n festgeschraubter Roboter<br />
• Körperkoordinatensystem (body base<br />
e zB<br />
frame); angesie<strong>de</strong>lt in einzelnen Körpern,<br />
e yB<br />
bei Robotern z.B. fixiert im Gelenk o<strong>de</strong>r im<br />
Schwerpunkt <strong>de</strong>s Arms o<strong>de</strong>r in „günstigen<br />
e xB geometrischen Punkten“<br />
B<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Nächster Schritt:<br />
Position und Orientierung bezogen auf Frame B unter<br />
zu Hilfenahme von Frame K <strong>de</strong>s Körpers beschreiben<br />
Robotertechnik<br />
P<br />
VLRob.ppt<br />
Folie 72<br />
Nur für Lehrzwecke
Rotation in kartesischen Koordinaten<br />
Generell gibt es drei Freiheitsgra<strong>de</strong> für die Orientierung im Raum und es<br />
wer<strong>de</strong>n meist zwei Verfahren zur Beschreibung <strong>de</strong>r Orientierung angewandt:<br />
•Euler-Winkel<br />
(Mechanik, …)<br />
• Roll, Pitch, Yaw (Rollen, Gieren, Nicken)<br />
(Schifffahrt, Luftfahrt)<br />
Ausgangssituation:<br />
z<br />
Mit R = Rotationsmatrix o<strong>de</strong>r Orientierungsmatrix<br />
(u i , v i , w i = x-y-z - Koordinaten <strong>de</strong>r Einheitsvektoren):<br />
w<br />
u<br />
v<br />
R<br />
⎛ux<br />
⎜<br />
= ⎜uy<br />
⎜<br />
⎝uz<br />
vx<br />
vy<br />
vz<br />
wx<br />
⎞<br />
⎟<br />
wy<br />
⎟<br />
w ⎟<br />
z ⎠<br />
(allgemein)<br />
x<br />
y<br />
R<br />
⎛ 1<br />
⎜<br />
= ⎜0<br />
⎜<br />
⎝0<br />
0<br />
1<br />
0<br />
0⎞<br />
⎟<br />
0⎟<br />
1⎟<br />
⎠<br />
(Ausgangssituation /<br />
Skizze)<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 73<br />
Nur für Lehrzwecke<br />
Rotation um die x-, y- und z-Achse<br />
Rotation um x:<br />
z<br />
α<br />
w<br />
u<br />
v<br />
α<br />
y<br />
x<br />
z<br />
w<br />
u v<br />
γ<br />
y<br />
x<br />
R (x, α)<br />
⎛ 1<br />
⎜<br />
= ⎜0<br />
⎜<br />
⎝0<br />
0<br />
cosα<br />
sinα<br />
0 ⎞<br />
⎟<br />
− sinα⎟<br />
cosα<br />
⎟<br />
⎠<br />
R (y, β)<br />
⎛ cosβ<br />
⎜<br />
= ⎜ 0<br />
⎜<br />
⎝−<br />
sinβ<br />
0<br />
1<br />
0<br />
sinβ<br />
⎞<br />
⎟<br />
0 ⎟<br />
cosβ⎟<br />
⎠<br />
γ<br />
⎛cos<br />
γ<br />
⎜<br />
= ⎜ sin γ<br />
⎜<br />
⎝ 0<br />
− sin γ<br />
cos γ<br />
0<br />
0⎞<br />
⎟<br />
0⎟<br />
1⎟<br />
⎠<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 74<br />
Nur für Lehrzwecke
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
VLRob.ppt<br />
Folie 75
Homogene Koordinaten in <strong>de</strong>r Robotertechnik<br />
d 1<br />
1<br />
p 1P<br />
P<br />
2<br />
p 2P<br />
P<br />
p 1P<br />
0<br />
p 0P<br />
Orte im Raum können vollständig<br />
beschrieben wer<strong>de</strong>n durch:<br />
d, p = Positionsvektor<br />
R = Rotationsmatrix<br />
d 2<br />
p 0P d 1<br />
1<br />
0 0 0<br />
p0P<br />
= d1+<br />
p1P<br />
0 0 1<br />
= d1+<br />
R1<br />
p1P<br />
In homogenen Koordinaten:<br />
0 0 1<br />
0 ⎛ R1<br />
d ⎞⎛<br />
1 p ⎞<br />
p<br />
1P<br />
0P = ⎜ ⎟⎜<br />
⎟<br />
0 1<br />
1<br />
⎝ ⎠⎝<br />
⎠<br />
0<br />
0 1<br />
r0P<br />
= T1<br />
r1P<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Hinweis:<br />
0R1 = Rotationsmatrix<br />
für Frame 1 bezogen<br />
auf Frame 0<br />
0<br />
In Vektorschreibweise:<br />
0 0 0 0<br />
p0P<br />
= d1+<br />
d2+<br />
p2P<br />
0 0 1 0 1 2<br />
= d1+<br />
R1<br />
d2+<br />
R1<br />
R 2 p2P<br />
In homogenen Koordinaten:<br />
0<br />
r 0P =<br />
Robotertechnik<br />
0 1<br />
T1<br />
T2<br />
2<br />
r2P<br />
VLRob.ppt<br />
Folie 77<br />
Nur für Lehrzwecke<br />
Homogene Transformationen<br />
Trans(x,y,z) = Verschiebung eines<br />
Punktes um x,y,z entlang <strong>de</strong>r<br />
jeweiligen Achse:<br />
Rotation um die y-Achse:<br />
Trans<br />
( x,y,z)<br />
⎛ 1<br />
⎜<br />
⎜0<br />
=<br />
⎜0<br />
⎜<br />
⎝0<br />
0<br />
1<br />
0<br />
0<br />
0<br />
0<br />
1<br />
0<br />
x⎞<br />
⎟<br />
y⎟<br />
z⎟<br />
⎟<br />
1⎠<br />
R ,<br />
( y β)<br />
⎛ cosβ<br />
⎜<br />
⎜ 0<br />
=<br />
⎜−<br />
sinβ<br />
⎜<br />
⎝ 0<br />
0<br />
1<br />
0<br />
0<br />
sinβ<br />
0<br />
cosβ<br />
0<br />
0⎞<br />
⎟<br />
0⎟<br />
0⎟<br />
⎟<br />
1⎠<br />
Rotation um die x-Achse:<br />
Rotation um die z-Achse:<br />
R ,<br />
( x α)<br />
⎛ 1<br />
⎜<br />
⎜0<br />
=<br />
⎜0<br />
⎜<br />
⎝0<br />
0<br />
cosα<br />
sinα<br />
0<br />
0<br />
− sinα<br />
cosα<br />
0<br />
0⎞<br />
⎟<br />
0⎟<br />
0⎟<br />
⎟<br />
1⎠<br />
R ,<br />
( z γ)<br />
⎛cos<br />
γ<br />
⎜<br />
⎜ sin γ<br />
=<br />
⎜ 0<br />
⎜<br />
⎝ 0<br />
− sin γ<br />
cos γ<br />
0<br />
0<br />
0<br />
0<br />
1<br />
0<br />
0⎞<br />
⎟<br />
0⎟<br />
0⎟<br />
⎟<br />
1⎠<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 78<br />
Nur für Lehrzwecke
Beschreibung nach Denavit - Hartenberg<br />
Begründung:<br />
• Bisher wur<strong>de</strong>n die Koordinatensysteme intuitiv<br />
gewählt<br />
• Es ist aber zweckmäßig, nach einem einheitlichen<br />
Schema beziehungsweise Verfahren vorzugehen<br />
• Vorteil: Verschie<strong>de</strong>ne Anwen<strong>de</strong>r kommen zu einer<br />
gleichen o<strong>de</strong>r zumin<strong>de</strong>st vergleichbaren<br />
Beschreibung <strong>de</strong>r Aufgabe<br />
Prinzip:<br />
• Es geht darum, von einem i-ten<br />
Koordinatensystem zu einem (i+1)-ten<br />
Koordinatensystem zu kommen<br />
• Man beschränkt die Freiheitsgra<strong>de</strong> <strong>de</strong>r<br />
Koordinatensysteme:<br />
- eine Drehachse<br />
- eine Linearachse<br />
(oft prismatische Achse genannt)<br />
Denavit, J., Hartenberg, R. S.: A kinematic notation for lower pair mechanisms<br />
based on Matrices. Journal of Applied Mechanics, vol. 77, pp. 215–221, June 1955.<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
Bei einem Roboter<br />
bestehen im Normalfall<br />
folgen<strong>de</strong> Möglichkeiten für<br />
zwei so genannte<br />
kinematische Paare:<br />
Gelenk i<br />
Gelenk i<br />
Glied i<br />
Drehachse<br />
Drehachse<br />
Linearachse<br />
Linearachse<br />
Gelenk i+1<br />
Form und Masse<br />
<strong>de</strong>r Glie<strong>de</strong>r wer<strong>de</strong>n<br />
abstrahiert<br />
Gelenk i+1<br />
Drehachse<br />
Linearachse<br />
Drehachse<br />
Linearachse<br />
VLRob.ppt<br />
Folie 79<br />
Nur für Lehrzwecke<br />
Bezeichnungen nach Denavit-Hartenberg<br />
Die Gelenkachsen von Gelenk (i) und Gelenk (i+1) fallen mit <strong>de</strong>n z-Achsen <strong>de</strong>r<br />
Koordinatensysteme (i-1) und (i) zusammen.<br />
Beispiel für Drehgelenke:<br />
Gelenk i<br />
q i Gelenk i+1<br />
q i+1<br />
Glied i<br />
z i-1<br />
K<br />
x i<br />
i<br />
α i<br />
a i<br />
z i<br />
y i-1<br />
a d<br />
i-1<br />
i<br />
q i<br />
K i-1<br />
x i-1<br />
y i<br />
Man erkennt:<br />
• a i und α i sind durch die<br />
Gelenkkonstruktionen festgelegt.<br />
• a i ist die gemeinsame Normale <strong>de</strong>r<br />
Drehachsen (z-Achsen), also <strong>de</strong>r<br />
kürzeste Abstand <strong>de</strong>r Achsen.<br />
• a i ist ein Abstand, und daher > 0<br />
• α i ist <strong>de</strong>r Winkel, um <strong>de</strong>n man die erste<br />
Achse z i drehen muss, damit sie parallel<br />
zur zweiten Achse z i+1 wird.<br />
• α i wird in <strong>de</strong>r Ebene senkrecht zur<br />
gemeinsamen Normalen a i gemessen.<br />
• Schaut man von <strong>de</strong>r Pfeilspitze von x i auf<br />
diese Ebene, erkennt man die positive<br />
Richtung von α i .<br />
• x i läuft kolinear zu a i , und seine Richtung<br />
geht von K i-1 weg nach K i .<br />
• Die y-Achsen ergänzen die<br />
Koordinatensysteme zum Rechtssystem.<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 80<br />
Nur für Lehrzwecke
Beschreibung <strong>de</strong>r Drehungen und <strong>de</strong>r Translationen - 1<br />
z i-1<br />
y i-1<br />
a i-1<br />
q i<br />
K i-1<br />
x i-1<br />
y i<br />
K i<br />
α i<br />
d i<br />
a i<br />
z i<br />
x i<br />
Es sind drei Schritte<br />
abzuarbeiten:<br />
1. Drehung um die Achse<br />
z i-1 um <strong>de</strong>n Winkel q i<br />
2. Translation K i-1 K i<br />
3. Drehung um die Achse x i<br />
um <strong>de</strong>n Winkel α i<br />
1.Drehung<br />
um qi<br />
2. Translation<br />
3. Drehung um<br />
αi<br />
⎛cos qi<br />
⎜<br />
⎜ sinqi<br />
⎜ 0<br />
⎜<br />
⎝ 0<br />
− sinqi<br />
cos qi<br />
0<br />
0<br />
0<br />
0<br />
1<br />
0<br />
0⎞<br />
⎟<br />
0⎟<br />
0⎟<br />
⎟<br />
1⎠<br />
,<br />
⎛ 1<br />
⎜<br />
⎜0<br />
⎜0<br />
⎜<br />
⎝0<br />
0<br />
1<br />
0<br />
0<br />
0<br />
0<br />
1<br />
0<br />
ai<br />
⎞<br />
⎟<br />
0 ⎟<br />
d ⎟<br />
i<br />
⎟<br />
1 ⎠<br />
und<br />
⎛ 1<br />
⎜<br />
⎜0<br />
⎜0<br />
⎜<br />
⎝0<br />
0<br />
cos αi<br />
sinαi<br />
0<br />
0<br />
− sinαi<br />
cos αi<br />
0<br />
0⎞<br />
0<br />
0<br />
1<br />
⎟ ⎟⎟⎟⎟ ⎠<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 81<br />
Nur für Lehrzwecke<br />
Beschreibung <strong>de</strong>r Drehungen und <strong>de</strong>r Translationen - 2<br />
Die Koordinatentransformation von (i-1) zu (i) ist dann das Produkt <strong>de</strong>r Matrizen:<br />
i−1<br />
Ti<br />
⎛cos qi<br />
⎜<br />
⎜ sinqi<br />
=<br />
⎜ 0<br />
⎜<br />
⎝ 0<br />
− sinqi<br />
cos qi<br />
0<br />
0<br />
0<br />
0<br />
1<br />
0<br />
0⎞<br />
⎛ 1<br />
⎟ ⎜<br />
0⎟<br />
⎜0<br />
⎟<br />
•<br />
0 ⎜0<br />
⎟<br />
⎜<br />
1⎠<br />
⎝0<br />
0<br />
1<br />
0<br />
0<br />
0<br />
0<br />
1<br />
0<br />
ai<br />
⎞ ⎛ 1<br />
⎟ ⎜<br />
0 ⎟ ⎜0<br />
⎟<br />
•<br />
d ⎜<br />
i 0<br />
⎟<br />
⎜<br />
1 ⎠ ⎝0<br />
0<br />
cos αi<br />
sinαi<br />
0<br />
0<br />
− sinαi<br />
cos αi<br />
0<br />
0⎞<br />
⎟<br />
0⎟<br />
0⎟<br />
⎟<br />
1⎠<br />
⎛cos qi<br />
⎜<br />
⎜ sinqi<br />
=<br />
⎜ 0<br />
⎜<br />
⎝ 0<br />
− sinqi<br />
cos qi<br />
0<br />
0<br />
0<br />
0<br />
1<br />
0<br />
0⎞<br />
⎛ 1<br />
⎟ ⎜<br />
0⎟<br />
⎜0<br />
⎟<br />
•<br />
0 ⎜0<br />
⎟<br />
⎜<br />
1⎠<br />
⎝0<br />
0<br />
cos αi<br />
sinαi<br />
0<br />
0<br />
− sinαi<br />
cos αi<br />
0<br />
ai<br />
⎞<br />
⎟<br />
0 ⎟<br />
d ⎟<br />
i<br />
⎟<br />
1 ⎠<br />
⎛cos qi<br />
⎜<br />
⎜ sinqi<br />
=<br />
⎜<br />
0<br />
⎜<br />
⎝ 0<br />
− sinqi<br />
cos αi<br />
cos qi<br />
cos αi<br />
sinαi<br />
0<br />
sinqi<br />
sinαi<br />
− cos qi<br />
sinαi<br />
cos α<br />
i<br />
0<br />
ai<br />
cos qi<br />
⎞<br />
⎟<br />
ai<br />
sinqi<br />
⎟<br />
d<br />
⎟<br />
i ⎟<br />
1<br />
⎠<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 82<br />
Nur für Lehrzwecke
Beschreibung <strong>de</strong>r Drehungen und <strong>de</strong>r Translationen - 3<br />
Anmerkungen:<br />
• Die Koordinatentransformation hängt von vier Parametern ab: a i , α i , d i , q i<br />
• Diese Parameter wer<strong>de</strong>n auch „link parameter“ genannt<br />
• a i und α i sind durch die maschinenbauliche Konstruktion <strong>de</strong>s (i)-ten Glie<strong>de</strong>s gegeben<br />
• q i und d i sind abhängig von <strong>de</strong>r Verbindung <strong>de</strong>r Glie<strong>de</strong>r (i-1) und (i) über das Gelenk (i)<br />
Fallunterscheidungen: (Deutung von q i )<br />
Gelenk (i) ist eine Drehachse:<br />
d i ist konstruktiv vorgegeben und konstant<br />
q i ist eine Gelenkkoordinate, d.h. im Beispiel <strong>de</strong>r Winkel zwischen <strong>de</strong>n<br />
Glie<strong>de</strong>rn (i-1) und (i)<br />
Gelenk ist eine Linearachse (Translation):<br />
d i ist variabel und wird dann als qi bezeichnet<br />
Der Winkel zwischen <strong>de</strong>n Glie<strong>de</strong>rn ist konstruktiv festgelegt, also konstant.<br />
Er wird dann ϑ i genannt.<br />
Damit folgt die Schreibweise <strong>de</strong>r vorherigen Koordinatentransformation<br />
für die Linearachse:<br />
⎛cos<br />
ϑi<br />
− sin ϑi<br />
cos αi<br />
sin ϑi<br />
sin αi<br />
ai<br />
cos ϑi<br />
⎞<br />
i−1<br />
Ti<br />
⎜<br />
⎜ sin ϑi<br />
=<br />
⎜ 0<br />
⎜<br />
⎝ 0<br />
cos ϑi<br />
cos αi<br />
sin αi<br />
0<br />
− cos ϑi<br />
sin αi<br />
cos αi<br />
0<br />
⎟<br />
ai<br />
sin ϑi<br />
⎟<br />
q ⎟<br />
i<br />
⎟<br />
1 ⎠<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 83<br />
Nur für Lehrzwecke<br />
Verallgemeinerung <strong>de</strong>r Beschreibung<br />
Die zuvor im Beispiel aufgestellten Koordinatentransformationen für die<br />
Drehungen und die Translationen kann man auch zusammenfassen (es<br />
han<strong>de</strong>lt sich dabei nur um eine an<strong>de</strong>re Sichtweise!):<br />
i−1<br />
Ti<br />
⎛cos<br />
ϑi<br />
⎜<br />
⎜ sinϑi<br />
=<br />
⎜ 0<br />
⎜<br />
⎝ 0<br />
− sinϑi<br />
cos αi<br />
cos ϑi<br />
cos αi<br />
sinαi<br />
0<br />
sinϑi<br />
sinαi<br />
− cos ϑi<br />
sinαi<br />
cos αi<br />
0<br />
ai<br />
cos ϑi<br />
⎞<br />
⎟<br />
ai<br />
sinϑi<br />
⎟<br />
d ⎟<br />
i<br />
⎟<br />
1 ⎠<br />
Und nun setzt man als Variable q i<br />
Für die Drehachse: ϑ i = q i<br />
Für die Linearachse: d i = q i<br />
Damit lassen sich dann alle vier möglichen<br />
beziehungsweise zulässigen Fälle betrachten:<br />
Gelenk i<br />
Drehachse<br />
Drehachse<br />
Linearachse<br />
Linearachse<br />
Gelenk i+1<br />
Drehachse<br />
Linearachse<br />
Drehachse<br />
Linearachse<br />
Technische Fachhochschule Berlin<br />
Fachbereich VI - Informatik und Medien<br />
Linnemann, SoSe 2008<br />
Robotertechnik<br />
VLRob.ppt<br />
Folie 84<br />
Nur für Lehrzwecke