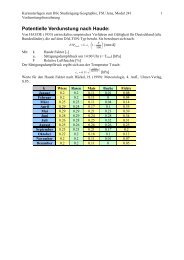
Hausarbeit - Friedrich-Schiller-Universität Jena

Friedrich – Schiller - Universität
Institut für Geographie
Wintersemester 2004/2005
Hausarbeit zum Hauptseminar:
Analyse und Modellierung räumlicher Daten
Leiter: Dr. Martin Herold
Thema:
Räumliche Autokorrelation und deskriptive Methoden
Verfasser:
Christian Pfeifer
Wanderslebenstr. 7, 07745 Jena
E-mail: christian_pfeifer@gmx.net
Abgegeben am 22.10.2004

Inhalt
1 Einleitung 2
2 Allgemeine deskriptive Methoden 2
2.1 Mittelwerte 2
2.1.1 Arithmetische Mittel 2
2.1.2 Median und Modus 3
2.2 Streuungsmaße 3
2.2.1 Standartabweichung und Varianz 3
2.2.2 Schiefe und Exzess 4
2.3 „Nearest Neighbor“-Analyse 4
2.4 Histogramm 5
2.5 Datenniveaus 6
2.6 Objektarten 7
3 Räumliche Autokorrelation 7
3.1 Hinführung 7
3.2 Das erste Gesetz der Geographie 8
3.3 Berechnung der räumliche Autokorrelation 10
3.3.1 Geary’s (c) Index 11
3.3.2 Moran’s (I) Index 12
3.4 Probleme 12
3.4.1 Datenherkunft 12
3.4.2 MAUP 13
3.5 Spatial Sampling 13
4 Schlussbemerkung 15
Literatur 15
1

1 Einleitung
Um herauszufinden wie bestimmte Eigenschaften im Raum verteilt sind bedarf es spezieller
statistischer Methoden, besonders dann, wenn die zu untersuchenden Eigenschaften in
Beziehung zum Raum oder zu anderen Merkmalen stehen. Um diese Beziehungen für den
Betrachter sichtbar zu machen werden diese durch deskriptive Methoden analysiert und in
Form einer einzigen oder weniger Zahlen ausgedrückt. In dieser Arbeit soll dabei ein
Hauptaugenmerk auf die Datenanalyse in Bezug auf die räumliche Autokorrelation gelegt
werden. Diese, soviel soll schon gesagt werden, beschäftigt sich mit der räumlichen
Beziehung zwischen Objekten und ihren Nachbarn. Oder wie MORAN schon 1948 schrieb
„The presence, absence, or characteristics of some spatial objects may sometimes have
significant impacts on the presence, absence, or characteristics of the neighboring objects.”
( LO & YEUNG 2002: 117)
Aber bevor auf diese spezielle deskriptive Methode der räumlichen Autokorrelation
eingegangen wird, sollen zuvor ausgewählte, grundlegende Verfahren und Sachverhalte der
traditionellen deskriptiven Statistik erläutert werden.
2 Allgemeine deskriptive Methoden
Die deskriptive bzw. beschreibende Statistik befasst sich mit der Analyse und Darstellung von
räumlichen und zeitlichen Daten. Die Methoden der deskriptiven Statistik haben das Ziel, die
oft großen Datenmengen mit nur wenigen Zahlen zu charakterisieren, so dass sie für den
Betrachter gut interpretierbar sind. Dabei zählt die Visualisierung der Daten, wie z.B. in einer
Karte, zu den besten Methoden bestimmte Muster in den Daten zu erfassen. Zu den
deskriptiven Methoden gehört der Mittelwert und die Streuung, welche nun kurz vorgestellt
werden (LO & YEUNG 2002: 350 & HELMSCHROT & FINK 2001).
2.1 Mittelwerte
Durch die Mittelwerte (engl. central tendency) wird das Zentrum der Verteilung
charakterisiert. Mittelwerte können u.a. durch das arithmetische Mittel, den Median oder den
Modus angeben werden (HELMSCHROT & FINK 2001).
2.1.1 Arithmetische Mittel
Das arithmetische Mittel berechnet man aus der Summe aller
Einzelwerte, dividiert durch die Gesamtzahl aller Stichprobenfälle
(siehe Formel 1). Man sollte diese Formel anwenden, wenn die
Formel 1: Mittelwert x m
Werte hauptsächlich um das arithmetische Mittel verteilt sind. Ist (HELMSCHROT & FINK 2001)
die Stichprobe zu heterogen (weicht zu sehr von der Glockenform
ab) bringt dieses Verfahren zu große Nachteile mit sich (HELMSCHROT & FINK 2001).
2

2.1.2 Median und Modus
Der Median ist der Wert, der die nach der Größe geordnete Verteilung in 2 gleichgroße
Bereiche teilt. Beispiel: Gegeben ist ein beliebige Zahlenreihe mit den Werten 1, 3, 5, 7, 66.
Der mittlere Wert also der Median ist hier 5.
Bei einer ungeraden Anzahl von Stichproben wird der Median von den beiden in der Mitte
stehenden Zahlen gebildet. Der Median hat den Vorteil, dass er sich im Gegensatz zum
arithmetischen Mittel nicht durch einzelne hohe Werte beeinflussen lässt.
Der Modus hingegen zeigt den am häufigsten vorkommenden Merkmalswert einer Datenreihe
oder einer Klasse auf (LO & YEUNG 2002: 351 & HELMSCHROT & FINK 2001).
2.2 Streuungsmaße
Die Streuung (engl.: dispersion) gibt an, wie weit die Merkmalswerte um das Zentrum verteilt
sind. Um die Streuung anzugeben gibt es vier gebräuchliche Möglichkeiten.
2.2.1 Standartabweichung und Varianz
Nach LO & YEUNG (2002: 351) ist die Standartabweichung die wichtigste Maßeinheit um die
Streuung zu charakterisieren. Um die Standartabweichung berechnen zu können, muss vorher
die Varianz gebildet werden. Denn die Standartabweichung ergibt sich, aus der Wurzel der
Varianz (siehe Fromel 3). Die Varianz selbst wird nach der Formel 2 berechnet. Hier muss die
Summe der quadrierten Abweichungen vom Mittelwert x m , durch die Gesamtzahl der
Elemente n dividiert werden.
Formel 3: Varianz s² (HELMSCHROT & FINK 2001)
Formel 2: Standartabweichung s
(HELMSCHROT & FINK 2001)
Die Standartabweichung gibt an, wie sich die Streuung einer Verteilung um den Mittelwert
verhält. Allerdings hat sie den Nachteil, dass man die Standartabweichungen zweier
verschiedener Stichproben nur vergleichen kann, wenn deren arithmetische Mittel in etwa
gleichgroß sind (LO & YEUNG 2002: 351 & HELMSCHROT & FINK 2001).
3

2.2.2 Schiefe und Exzess
Die Schiefe (engl.: skewness) wie der Exzess (engl.: kurtosis) sind Formenparameter, d.h. sie
geben Auskunft über die Form der Verteilung.
„Die Schiefe […] stellt ein Maß für die Symmetrie der Verteilung um das arithmetische
Mittel dar und errechnet sich…“ (HELMSCHROT & FINK 2001) aus der Differenz des
Mittelwert x m vom Median Me, welche durch die Standartabweichung s dividiert wird, wie in
Formel 4 abgebildet. Wenn die Form der Verteilung symmetrisch ist, dann hat die Schiefe g
einen Wert von 0, ist g größer als 0 handelt es sich um eine positive Schiefe, der Median ist
links vom Mittel. Bei einer negativen Schiefe hingegen ist g kleiner als 0 und der Median
rechts vom Mittel.
Formel 4: Schiefe g (HELMSCHROT & FINK 2001) Formel 5: Exzess Ez (HELMSCHROT & FINK 2001)
Der Exzess hingegen ist ein Maß für die Steilheit der Verteilung. So beschreibt er, ob die
Merkmalsverteilung spitz oder flach um das Zentrum verteilt ist. Berechnet wird er, wie in
Formel 5 aufgezeigt. Von einer spitzen Verteilung spricht man, wenn der Exzess Ez größer
als eins ist und damit steiler zuläuft als eine Normalverteilung. Keinen Exzess (Ez = 1) findet
man bei einer Normalverteilung vor. Ist der Exzess kleiner als eins (negativer Exzess) ist die
Verteilung flacher als eine Normalverteilung (LO & YEUNG 2002: 351).
2.3 „Nearest Neighbor“-Analyse
Bei der „Nearest Neighbor“-Analyse werden Verteilungsmuster von Punkten auf einer Fläche
untersucht. Dabei kann bestimmt werden, ob die Messpunkte regelmäßig, unregelmäßig oder
in Clustern (Gruppen) auftreten. „Diese Einordnung [in regelmäßig, unregelmäßig oder in
Clustern] erfolgt über das Messen der Distanzen zwischen gepaarten Datenpunkten. Gepaart
werden dabei die Punkte mit der geringsten räumlichen Distanz zueinander - die ‚Nearest
Neighbor’.“ (DUMFARTH & LORUP 2000)
Um Verwechslungen mit der räumliche Autokorrelation aus dem Weg zu gehen, muss klar
festgestellt werden, dass bei der „Nearest Neighbor“-Analyse nur die räumliche Verteilung
der Punkte bestimmt wird, nicht aber im Zusammenhang mit den Ausmaß der Werte, den
diese Punkte haben
4

Abbildung 1: Mögliche Verteilungsmuster (a) regelmäßig, (b) unregelmäßig, (c) gruppiert
(DUMFARTH & LORUP 2000)
Bei der „Nearest Neighbor“-Analyse gibt es einige Dinge zu beachten, um mögliche
Ungenauigkeiten und Fehlmessungen so gering wie möglich zu halten. Weil es notwendig ist,
die Punktdichte in dem Gebiet zu kennen, muss die Größe der Fläche, in dem die Analyse
durchgeführt werden soll, genau festgelegt werden. Ist nämlich die zu untersuchende Fläche
zu groß im Verhältnis zur Anzahl der Punkte, erhält man eine viel geringere Punktdichte als
wenn man für die gleiche Anzahl von Punkten eine kleineres Gebiet für die Untersuchung
verwendet.
Auch das Problem des Kanteneffektes (engl.: edge effect) sollte nicht vernachlässigt werden.
Das Problem liegt hier darin, dass es unter Umständen auch Punkte außerhalb der Grenzen
der Untersuchungsmatrix gibt, zu denen aber von den Punkten am Rande der Matrix keine
Distanz gemessen werden kann, obwohl diese am nächsten liegen. Um dies zu verhindern,
sollte auch eine Messung zu Punkten außerhalb der Untersuchungsmatrix zugelassen werden
(LO & YEUNG 2002: 357).
2.4 Histogramm
Neben der Karte ist das Histogramm
(siehe Diagramm 1) eine der verbreitesten
Möglichkeiten Daten visuell darzustellen.
Ein Histogramm zeigt an, wie viele
Merkmalsausprägungen in einer
bestimmten vorher festgelegten Klasse
sind. Dabei gibt die y-Achse Auskunft
über die Häufigkeit der Variable (z.B.:
Anzahl von Temperaturwerten) und die x-
Achse zeigt die Klassen, in denen die
Werte eingeordnet werden (z.B.: in der
Klasse 0-5°C liegen 3 Werte). Es liegt also
eine Klassenhäufigkeitsverteilung vor,
durch die man erkennen kann, wie sich die
Diagramm 1: Histogramm [rot] mit
Normalverteilung [schwarz] (DUMFARTH & LORUP 2000)
5

Werte über das gestammte Wertespektrum verteilen. Die wichtigste Form einer
Häufigkeitsverteilung ist die glockenförmige Normalverteilung. Diese ist so bedeutend, da
viele statistische Methoden auf Daten angewiesen sind, die aus einer normalverteilten
Grundgesamtheit kommen. Bei einer Normalverteilung liegt das arithmetisches Mittel und
Median nahe beieinander (oder sind gleich) und repräsentieren die Mitte der Datenmenge
(HELMSCHROT & FINK 2001).
2.5 Datenniveaus
Da bestimmte deskriptive Methoden nur bei Daten bestimmter Skalenart angewendet werden
können, sollen hier die verschieden Skalen kurz vorgestellt werden. Das Problem liegt hier in
dem Umstand, dass Daten verschiedenste Merkmalsausprägungen repräsentieren, die in
unterschiedlichsten Maßeinheiten gemessen werden. So kann ein Datensatz aus
Temperaturdaten bestehen, die in °C gespeichert werden oder aber die Entfernungen
repräsentieren, die in Metern gemessen werden. Dabei muss beachtet werden, dass man zwar
sagen kann, 2m sind doppelt so viel wie 4m, aber 10 °C sind nicht doppelt so warm wie 5°C,
weil die Maßeinheit Grad Celsius einen zufälligen Nullpunkt hat, im Gegensatz zu Kelvin
oder dem metrischen System (HELMSCHROT & FINK 2001).
• Nominalskalierte Daten sind mit Werten unterschiedlicher Merkmale besetzt und eine
Rangfolge der Merkmale kann nicht gebildet werden. Beispiele hierfür sind Namen,
Religionszugehörigkeit aber auch bei Ja-Nein-Fragen wie „Hat der Haushalt einen
PKW?“.
• Die Ordinalskala gilt für Werte, deren Merkmale in eine Rangfolge gebracht werden
kann und die Abstände zwischen benachbarten Werten sind nicht immer identisch.
Beispiele sind Erdzeitalter, Zensuren oder das Einkaufsverhalten (oft, regelmäßig,
selten).
• Bei intervallskalierten Daten sind die Abstände zwischen benachbarten Werten
identisch, aber es gibt keinen definierten Nullpunkt. Darunter fällt die schon oben
erwähnte Maßeinheit Grad Celsius, aber auch der Intelligenzquotient.
• Ratioskalen unterscheiden sich von der intervallskalierten nur in dem Punkt, dass hier
ein definierter Nullpunkt festgelegt ist. Dazu gehört die Angabe von Entfernung in
Metern, das Gewicht in Kilogramm oder das Einkommen in Euro.
(HELMSCHROT & FINK 2001)
6

2.6 Objektarten
Ähnlich wie bei den Skalenarten ist die Anwendung von statistischen Methoden nur an
bestimmte Objektarten gekoppelt (siehe Geary’s (c) Index ). Geographische Objekte werden
nach ihrer Topologieausdehnung, also der Art wie sie den Raum ausfüllen gemessen.
• Punkte haben keine dimensionale Ausbreitung, also auch keine Länge, Breite oder
Höhe. Punkte können verwendet werden um die räumliche Verteilung von
Ereignissen und deren Muster wiederzugeben.
• Linien haben genau eine Dimension, die Länge. Sie werden verwendet, um Distanzen
zu messen oder lineare Objekte darzustellen, beispielsweise Strassen.
• Flächenobjekte haben eine zwei dimensionale Ausdehnung, die Länge und Breite,
aber keine Höhe. Sie werden verwendet, um natürliche Objekte wie Felder oder
künstliche Objekte wie Bevölkerungsverteilungen darzustellen.
• Oberflächen und Volumen sind dreidimensional. Sie finden Verwendung bei der
Darstellung von natürlichen Objekten wie digitalen Geländemodellen oder bei
Phänomenen wie das Besucherpotential eines Einkaufszentrums.
• Zeit wird oft als eine weitere Dimension angesehen, kann aber nach LONGLEY et al.
(2002: 101) im GIS nur schwer simuliert werden.
Wichtig ist noch zu wissen, wie sich die einzelnen Dimensionen zueinander verhalten. So
kann man ein höher dimensionales Objekt auf eine niederes Herunterrechnen, aber nicht
umgekehrt. Wie man ein Objekt letztendlich im GIS darstellt, hängt auch von dem Maßstab
ab. „For example, on a less-detailed map of the world, New York is represented as zerodimensional
point. On a more-detailed map such as a road atlas it will be represented as twodimensional
point.” (LONGLEY et al. 2001: 101) In Wirklichkeit ist die Stadt aber dreidimensional
und kann als solche auch von bestimmten Softwaresystemen wiedergegeben
werden (LONGLEY et al. 2001: 101).
3 Räumliche Autokorrelation
3.1 Hinführung
Das Problem der traditionellen statistischen Analysen ist, dass es bei der Untersuchung von
Zusammenhängen, die eine stochastische Abhängigkeit aufweisen, zu fehlerhaften Resultaten
kommt. So sind Fehlschätzungen der Korrelation zwischen stochastisch abhängigen Variablen
möglich, wodurch Test- und Schätzverfahren verzerrte Ergebnisse liefern und
Fehlinterpretationen die Folge sind. Allerdings kommen stochastische abhängige Variablen in
der Statistik, sehr oft vor und ihre genaue Analyse ist meist von großem Interesse.
(BAHRENBERG et al. 2003²: 360-362) Stochastische Abhängigkeit heißt, dass bestimmte
statistische Ereignisse nicht unabhängig voneinander auftreten.
7

Die Ursache für das Unvermögen der traditionellen Statistik mit Daten umzugehen, die
stochastische Abhängig sind, liegt darin, dass sie auf Zufallsvariablen basiert. Darunter
versteht man, dass die verschiednen Datenwerte der Zufallsvariable rein zufällig zustande
kommen und somit unabhängig voneinander sind (ABLER et al. 1992: 154). Am Beispiel eines
Würfelexperiments soll dies verdeutlicht werden. Würfelt man eine 6 hat dies keinerlei
Einfluss auf den nächsten Würfeldurchgang. Die Wahrscheinlichkeit wieder eine 6 zu würfeln
ist bei jeden Durchgang gleich groß. Vorherige Ereignisse haben keinen Einfluss auf
nachfolgende Ereignisse.
„In Hinblick auf die räumliche Verteilung von Datenpunkten bedeutet dies, daß die
verschiedenen Werte einer Variablen unabhängig von ihrer räumlichen Position zustande
kommen. Erscheinungen wie Distanz der Werte zueinander, Nachbarschaft, Nähe, Richtung
und dergleichen haben also keinen Einfluß auf den Wert eines bzw. aller Datenwerte.“
(DUMFARTH & LORUP 2000) Dass dies aber nicht den Gegebenheiten der Realität entspricht,
ist leicht erkennbar und wird am Beispiel des Bodenmarktes deutlich. Denn dann würde die
räumliche Verteilung der Grundstückspreise keinerlei Muster aufzeigen, da ja alles
zufallsverteilt ist. Im Stadtzentrum beispielsweise würden sich willkürlich sehr teure
Grundstücke mit sehr billigen oder mittelteuren abwechseln.
Bei der Geostatistik geht man daher den Ansatz an, dass die Werte, die eine Variable
annehmen kann, durch eine Funktion gesteuert wird, weshalb man von regionalisierten
Variablen spricht. Das heißt, dass die Werte eines Gebietes bzw. einer Region einander
ähnlich sind, weil sie sich ja untereinander beeinflussen können und dass mit zunehmender
Entfernung die Ähnlichkeit abnimmt. Dies beschrieb W. TOBLER mit dem ersten Gesetz der
Geographie, welches im nächsten Abschnitt erläutert werden wird.
Weiterhin geht man davon aus, dass die Verbreitung eines Phänomens nur ausreichend mit zu
Hilfenahme von räumlichen Eigenschaften (z.B.: Distanz oder Nachbarschaft) erklärt werden
kann (DUMFARTH & LORUP 2000).
3.2 Das erste Gesetz der Geographie und mehr (und seine Folgen)
W. TOBER formulierte 1970 das erste gesetzt der Geographie und beschrieb somit das schon
seit langem bekannte Phänomen, das sich benachbarte Objekte oft ähnlicher waren als weit
entfernte. „The first law of geography is that everything is related to everything else, but near
things are more related than distant things.”(TOBLER 1970 in ABLER 1992: 155) Dieses Gesetz
der Geographie ist, so LONGLEY et al. (2001: 99), die allgemeinste Formulierung über die
Verteilung räumlicher Erscheinungen.
Mit seinem Gesetzt beschreibt TOBLER die räumliche Autokorrelation, also den Grad, mit
dem nahe und entfernte Dinge miteinander verbunden sind (LONGLEY et al. 2001: 99).
Die räumliche Autokorrelation ist eine Bezeichnung für die Abhängigkeit zwischen
benachbarten Orten, wie es überall auf der Erdoberfläche vorkommt. „In practice, the
8

existence of spatial autocorrelation means that if A and B are close together, what happens at
A is related to what happens at B, and vice-versa.”(ABLER et al 1992: 287) Obwohl es logisch
erscheint, dass Dinge die sich räumlich nahe sind, auch ähnliche Merkmale aufweisen, kann
der Umkehrschluss, dass sich die Merkmale von Objekten, die weit entfernt von einander
sind, stark unterscheiden, nicht so einfach gezogen werden. Für ABLER et al. (1992: 287) ist
vielmehr die Frage entscheidend, wie weit zwei Orte von einander entfernt sein müssen,
damit sich diese nicht gegenseitig beeinflussen, sie also unabhängig voneinander sind. Es soll
nur kurz erwähnt werden, dass der gleiche Umstand auf die Zeit bezogen zeitliche
Autokorrelation genannt wird (LONGLEY et al. 2001: 99).
Bei der Bestimmung der räumliche Autokorrelation sind die Lage der Objekte zueinander und
ihre Merkmalsausprägung die wichtigsten Faktoren. Dabei werden gleichzeitig die
Gemeinsamkeiten im Ort und in der Eigenschaft miteinander verglichen (siehe Abschnitt 3.3
Berechnung der räumlichen Autokorrelation). Wenn Objekte nahe beieinander liegen bzw.
benachbart sind und sie das gleichen Merkmal beinhalten, dann spricht man von einem
Muster mit positiver räumlichen Autokorrelation.
„Conversely, negative Spatial autocorrelation is said to exist when features which are close
together in space tend to be more dissimilar in attributes than features which are further apart
(in opposition to Tobler’s Law).“ (LONGLEY et al. 2001: 100,101) Eine räumliche
Autokorrelation ist nicht vorhanden, wenn die Merkmale unabhängig vom Ort sind (LONGLEY
et al. 2001: 101).
Abbildung 2: Typen der räumlichen Autokorrelation (LO & YEUNG 2002: 117)
An Abbildung 2 sind die drei wichtigsten Typen von räumliche Autokorrelationen aufgezeigt.
Die Klassifizierung richtet sich nach der relativen Verteilung räumlicher Objekte und ihrer
Nachbarn. Feld A zeigt die extremste Form positiver Autokorrelation zwischen benachbarten
Zellen. Hier liegen jeweils die schwarzen und weißen Zellen in einer homogenen Fläche
zusammen bzw. räumliche Objekte, die die gleichen Eigenschaften haben, liegen räumlich
nah beieinander. Das genaue Gegenteil, also eine extrem negative räumliche Autokorrelation,
zeigt das Feld C. Hier grenzen an jedes schwarze Feld jeweils nur weiße Felder und
9

Abbildung 3: Bevölkerungsverteilung in Kalifornien und Iowa (ABLER et al. 1992: 84)
umgekehrt. Eine zufällige räumliche Autokorrelation sieht man im Feld B. Dort gibt es keine
größeren Cluster von Objekten mit den gleichen Werten.( LONGLEY et al. 2001: 101 & LO &
YEUNG 2002: 117)
In Abbildung 3 sieht man ein praktisches Beispiel für die unterschiedliche Typen räumliche
Autokorrelation. Hier wird auch deutlich, dass weniger die durchschnittliche
Bevölkerungsdichte von Interesse ist (was auch in der traditionellen Statistik berechnet
werden kann), sondern dass es für eine Interpretation viel interessanter (aber auch
schwieriger) zu wissen ist, wo Ballungen und wo ländliche Gebiete sind. Beide Regionen sind
von der Fläche her in etwa gleich groß, haben aber eine vollkommen unterschiedliche
Bevölkerungsverteilung. In San Bernardino herrscht aufgrund des nur in wenigen Teilen
erreichbaren Grundwassers eine starke räumliche Autokorrelation der Bevölkerung. Im
Gegensatz dazu steht das Gebiet in Iowa, das nur eine schlechte räumliche Autokorrelation
aufweist, was u.a. auf die gleichmäßig vorkommenden Ressourcen zurückzuführen ist (ABLER
et al. 1992: 83).
3.3 Berechnung der räumliche Autokorrelation
Bei der Berechnung der räumliche Autokorrelation werden zwei Werte miteinander
verglichen. Erstens die Gleichwertigkeit der Attribute und zweitens die Ähnlichkeit des Ortes
der Objekte, welche mit den Attributen besetzt sind. Dabei hängt es von dem verwendeten
Datentyp ab, mit welcher Methode die Attribute miteinander verglichen werden können und
von dem Objekttyp,
10

wie die Nachbarschaft festgestellt werden kann (LONGLEY et al. 2001: 114). Zwei der
wichtigsten Methoden, die räumliche Autokorrelation anzugeben, ist der Geary’s (c) Index
und der Moran’s (I) Index (LO & YEUNG 2002: 351).
3.3.1 Geary’s (c) Index
Der von Geary entwickelte Index ist eine Maß zur Angabe der räumliche Autokorrelation für
Objekte mit intervallskalierten Attributdaten. Deshalb kann man diesen Index gut bei der
Analyse von Datenansammlungen verwenden, die von Erhebungsgebieten
(engl. census tracts) stammen.
Der Geary’s (c) Index misst die Ähnlichkeit der Werte von i und j (siehe Formel 6).
Die Variable z i entspricht dem Wert des Objektes c i . Die Ähnlichkeit des Ortes, wo sich i und
j befinden, wird durch die boolesche Variable w ij angegeben, wobei w ij = 1 ist, wenn sie
benachbart sind und wij = 0, wenn sie es nicht sind (LO & YEUNG 2002: 351,352). Aber das
ist nur eine von vielen Möglichkeiten, w ij zu definieren, denn w ij repräsentiert die
Nachbarschaftsbeziehungen und da diese je nach Aufgabe anders festgelegt werden können,
muss diese auch in der Formel entsprechend definiert werden
(BAHRENBERG et al. 2003²: 381-383). Daraus ergibt sich dann der Index (c) wie in Formel 7
beschrieben, wobei s ² die Varianz des Merkmale z i ist.
Wenn das Ergebnis von c = 1 ist, dann sind die Merkmale der Objekte unabhängig von ihrer
Lage verteilt. Der Index (c) ist kleiner als eins, wenn gleiche Merkmale an gleichen Orten
vorkommen, es also eine positive räumliche Autokorrelation gibt. Und schließlich kann (c)
auch größer als eins sein, wenn sich Merkmale und Lage der Objekte unterscheiden, also eine
negative räumliche Autokorrelation vorliegt (LO & YEUNG 2002: 351,352).
Formel 6: Berechnung des Geary’s
(c) Index (LO & YEUNG 2002: 351)
Formel 7: Berechnung des Geary’s (c) Index
(LO & YEUNG 2002: 351)
11

3.3.2 Moran’s (I) Index
Der Moran’s (I) Index hat starke Ähnlichkeit mit Geary’s Index mit dem Unterschied, dass
hier die Ergebnisse dem Betrachter wahrscheinlich logischer erscheinen. Denn hier stehen
positive Ergebnisse auch für eine positive räumliche Autokorrelation und negative für eine
negative räumliche Autokorrelation. Wenn der Index 0 ist, weist dies auf unabhängige
unkorrelierte Daten hin, mit zufälliger Anordnung.
Die Variablen in der unteren Formel 8 zur Berechnung des Index (I) werden fast genauso
definiert wie bei Geary’s (c) Index. Allerdings wird c ij nach der oberen Formel 8 beschrieben.
z i steht wieder für den Wert des Objektes i und j. Die Variable ist der Mittelwert, s²
entspricht der Varianz von z i . Die räumliche Nähe für i und j wird wieder durch w ij,
angegeben (LO & YEUNG 2002:352).
Moran’s and Gearie’s Index kann man nur bei
flächenhaften Objekten anwenden. Es gibt aber
Punkt, Linien und Rasterobjekte für die auch
über Umwege eine Berechnung der räumliche
Autokorrelation möglich ist.
Bei Punktdaten kann man beispielsweise die
Punkte in Flächen umwandeln und dann so die
oben erwähnten Indizes anwenden. Die
räumliche Autokorrelation zwischen
linienförmigen Objekte kann man berechen,
Formel 8: Berechnung des Moran’s (I) Index wenn die Linien Verbindungen zwischen
(LO & YEUNG 2002: 352)
Punkten repräsentieren, die mit Merkmalen
besetzt sind. So wird dann die
Merkmalsähnlichkeit von den Punktpaaren mit anderen Punktpaaren verglichen und die
räumliche Nähe wird dadurch gemessen ob es eine direkte Verbindung zwischen den
Punktpaaren gibt. Bei Rasterdaten wird einfach verglichen, ob einzelne Rasterzellen gleiche
Außengrenzen haben (LO & YEUNG 2002: 352).
3.4 Probleme
3.4.1 Datenherkunft
Ein allgemeines Problem, das viele Analysen betrifft, ist, dass man nicht weiß, ob die
Ergebnisse stimmen, weil man nicht sicher sein kann, dass die Daten, die diesen zu Grunde
liegen, korrekt sind. Mit den Worten von LONGLEY et al. (2001: 137) ausgedrückt: „
Uncertainties in data lead to uncertainties in the result of analysis.“ Die Ursache liegt u.a. in
der Generalisierung und Bündelung der rohen Ausgangsdaten (welche die Realität
widerspiegeln sollen), z.B.: wenn Krankheitsfälle nur pro Bezirk angegeben werden oder
12

Bevölkerungszahlen nur für ein bestimmtes Gebiet angeboten werden. Obwohl man die
Ursache für dieses Problem nicht beheben kann, ist es doch möglich, es genau zu
quantifizieren, um so zumindest die schlimmsten Effekte zu verringern. Die Probleme
kommen auch daher, weil in einen GIS Daten unterschiedlichster Herkunft, Maßstabes,
Detailgenauigkeit und Klassifizierung miteinander verschmelzt werden
(LONGLEY et al. 2001: 137).
3.4.2 MAUP
Das „modifiable areal unit problem“ (MAUP) tritt auf, wenn willkürlich festgelegte Grenzen
für die Berechnung von räumlichen Ereignissen genutzt werden. Dies tritt z.B. bei
Volkszählungsdaten auf, die in bestimmten Flächen angegeben werden, oder die Angabe des
Wahlergebnisses wird höchstens in der Größe von Stadtvierteln gemacht, nicht aber in der
von Einzelpersonen. Vom statistischen Standpunkt her sind diese Grenzen beliebig festgelegt
worden weil, „They do not necessarily consider with breaks in the data. Thus, changing the
boundaries of units […] can affect the appearance of the data.“ (HEYWOOD et al. 2002²: 125)
Deshalb ist es sehr problematisch, zwei Karten oder Datensätze miteinander zu vergleichen,
die denselben Ausschnitt zeigen, aber deren Flächeneinheiten sich unterscheiden (HEYWOOD
et al. 2002²: 125 & LONGLEY et al. 2001: 138).
3.5 Spatial Sampling
Als letztes soll noch kurz auf das spatial sampling eingegangen werden, da die durch das
sampling reduzierten Daten auch bei der Analyse der räumliche Autokorrelation verwendet
werden. Sampling ist ein Prozess, bei dem aus einem Feld mit vielen Objekten, einige wenige
herausgesucht werden. Dies ist nötig, da die reale Welt unendlich komplex ist, ein GIS aber
nicht unendlich viele Daten verarbeiten kann. Daher braucht es eine Reduzierung der Daten,
wie es durch das sampling geschieht. Die sampling Modelle (engl.: sampling scheme, siehe
Abbildung 4) bestimmen die räumliche Verteilung der einzelnen Stichprobenpunkte im
Untersuchungsgebiet (LONGLEY et al. 2001: 103).
• Das Feld A in Abbildung 4 zeigt eine einfache zufällige Stichprobe, also eine, in der
jeder Punkt die gleiche Wahrscheinlichkeit hatte, gezogen zu werden. Dieses Modell
hat den Vorteil, dass es statistisch völlig korrekt ist, aber es weist in der Praxis einige
Schwierigkeiten auf. So kann es vorkommen, das kleine, aber wichtige Bereiche
unterpräsentiert werden, es sei denn es handelt sich um eine sehr große Anzahl von
Stichproben.
• Bei einer systematischen Stichprobe wird der erste Punkt zufällig ermittelt und an
diesem dann die restlichen entlang eines festen Schemas ausgerichtet, wie in Feld B zu
sehen. Diese Methode ist einfach durchzuführen, kann aber bei Daten die periodischen
Änderungen unterliegen, starke Fehler verursachen.
13

• Eine strategische Zufallstichprobe findet man dann vor, wenn man das
Untersuchungsgebiet in bestimmte Teilgebiete gliedert und dann in jedem Teilgebiet
eine zufällige Stichrobe nimmt (siehe Abbildung 4, Feld C).Dieses Modell scheint am
geeignetsten, weil nur eine geringe Anzahl von Stichproben gezogen werden muss.
Allerdings leidet dieses Modell auch unter denselben Problemen wie die
Zufallsstichprobe.
• Das letzte hier aufgeführte sampling Modell zeigt ein strategisches, systematisches
und unangepasstes Modell. Wie der Name schon sagt, vereinigt es die
Vorgehensweise und auch Vorteile der drei vorher genannten Modelle (LO & YEUNG
2002: 118,119).
Zur Stichprobenanzahl lässt sich sagen, dass je heterogener räumliche Phänomene verteilt
sind, desto mehr Stichproben sollten genommen werden, um die ganze breite des Umfanges
zu erfassen. Und je homogener die Verteilung desto weniger Stichproben müssen genommen
werden. Zu beachten ist, dass aus Gründen der Repräsentativität eine gewisse Mindestanzahl
an Stichproben gesammelt werden müssen (LONGLEY et al. 2001: 118).
Abbildung 4: Vier geographische sampling Modelle (LO & YEUNG 2002: 118 )
14

4 Schlussbemerkung
Wie hoffentlich gezeigt werden konnte ist die Analyse räumlich korrelierter Daten eine
komplexe, aber aufschlussreiche Methodik mit vielfachen Anwendungsmöglichkeiten.
Trotzdem ist mir beim lesen der vielfältigen Literatur aufgefallen, dass immer wieder erwähnt
wird, dass die Methoden zur Analyse räumlichen korrelierter Daten nur schlecht oder gar
nicht in GIS integriert sind, wie auch LO & YEUNG (2002: 350) bemängeln. Lediglich mit
Idris32 so LO & YEUNG (2002: 350) ist es möglich räumlichen Autokorrelation mit den
Modul „AUTOCORR“ zu bestimmen. Hingegen bietet das weit verbreitet ArcInfo keine
direkte Unterstützung bei der Analyse von räumlichen Autokorrelation. Nur durch eine
Kopplung mit anderen Statistikprogrammen (z.B.: SPSS) kann diese Funktion implementiert
werden.
Bleibt zu hoffen, dass in Zukunft diesem Gebiet der Datenanalyse mehr Aufmerksamkeit
geschenkt wird, um deren Bedeutung gerecht zu werden.
Literatur
ABLER R.F., MARCUS G. M. & J. M. OLSEN (1992): Geography’s inner worlds, Pervasive
Themes in Contemporary American Geography. New Jersey.
BAHRENBERG G., GIESE E. & J. NIPPER (2003²): Statistische Methoden in der Geographie,
Bd. 2. Berlin, Stuttgart.
HEYWOOD I., CORNELIUS S. & S. CARVER (2002²): An Introduction to Geographical
Information Systems. Essex.
LO C. P. & A. K.W. YEUNG (2002): Concepts and Techniques of Geographic Information
Systems. New Jersey.
LONGLEY P. A., GOODCHILD M.F., MAGUIRE D. J. & D.W. RHIND (2001): Geographic
Information, Systems and Science. Chichester, New York.
Internetliteratur
HELMSCHROT J. & M. FINK (2001): Skript zum Proseminar Statistik,
www.geogr.uni-jena.de/~c8firma/Statistik/ (letzter Aufruf 2002)
DUMFARTH E. & E. J. LORUP (2000): Geostatistik I - Theorie und Praxis,
www.geo.sbg.ac.at/staff/lorup/lv/geostats2000/ (letzter Aufruf 21.10.04)
15