Exponentialfunktion und Logarithmus(funktion) - arthur

Exponentialfunktion und Logarithmus(funktion) 31
Exponentialfunktion und Logarithmus(funktion)
1. Exponentialfunktionen
Beispiel:
x
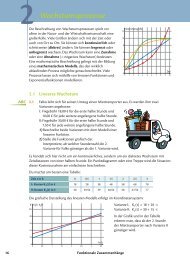
Die Graphen der Funktionen (1) f 1 :x7! 2 x (2) f 2 :x7! 1 x x
2
(3) f 3 :x7! 2 (4) f4 :x7! 3 sind über der Definitionsmenge
3
2
D ¼fxjx 2 R ^ð 3Þ4x43g in einem gemeinsamen Koordinatensystem
zu zeichnen!
Lösung:
x f 1 ðxÞ f 2 ðxÞ f 3 ðxÞ f 4 ðxÞ
3 0,125 8 3,375 0, _ 2 _ 9 _ 6
2 0,25 4 2,25 0, _ 4
1 0,5 2 1,5 0, 6 _
0 1 1 1 1
1 2 0,5 0, 6 _ 1,5
2 4 0,25 0, 4 _ 2,25
3 8 0,125 0, 2 _ 9 _ 6 _ 3,375
x
y = (
2
3 )
x
y = (
1
2 )
y
y = 2 x
x
y = (
3
2 )
– 3 – 2 – 1 0 1 2 3
x
Definition:
Exponentialfunktionen sind
Funktionen, die durch eine
Funktionsgleichung y ¼ a x
ða 2 R þ nf1gÞ 2) dargestellt werden
können. Die unabhängige Variable
x tritt somit als Exponent einer
konstanten positiven Basis auf.
Der Ausdruck a x ,a> 0 2) stellt für
jedes x 2 R einen eindeutig
bestimmten Zahlenwert dar. Er legt
somit eine Funktion f: x 7! a x fest.
Man beachte den Unterschied zur
Potenzfunktion:
Bei der Potenzfunktion f: x 7!x n
ist die Basis veränderlich.
Bei der Exponentialfunktion
f: x 7! a x ist der Exponent
veränderlich.
Einige Eigenschaften der Funktion x 7! a x ða 2 R þ nf1g; x 2 RÞ:
1 Definitionsmenge D ¼ R
2 Wertemenge W ¼ R þ
3 Die x-Achse ist Asymptote.
4 x 7! a x geht immer durch den Punkt Pð0 j 1Þ.
5 x 7! a x ist streng monoton wachsend füra> 1.
6 x 7! a x ist streng monoton fallend füra< 1.
7 x 7! a x und x 7! a x liegen symmetrisch bezüglich der y-Achse.
Die Bedeutung der Exponentialfunktion liegt vor allem im Bereich der
Naturwissenschaften und der Wirtschaft, wo mit ihrer Hilfe Wachstumsbzw.
Abnahmevorgänge beschrieben werden können: Zinseszinsen,
progressive und degressive Abschreibung, Bevölkerungs- und Pflanzenwachstum,
radioaktiver Zerfall von Atomkernen, Erwärmungs- und Abkühlungsprozesse
usw.
1) Füra¼ 1 ergibt sich die konstante Funktion y ¼ 1.
2) Die Einschränkung a > 0 ist notwendig, weil Potenzen mit rationalen Exponenten
nur für positive Basen erklärt sind.

32 Exponentialfunktion und Logarithmus(funktion)
Gemäß dem in der Außenspalte dargestellten Funktionsgraphen vermehrt
sich z. B. die Menschheit oder der Holzbestand eines Waldes. Selbst
Bakterien vermehren sich zunächst nach dieser Funktion. Vergleichen wir
den Graphen dieser Funktion mit der grafischen Veranschaulichung des
vorigen Beispiels, könnte man vermuten, dass diese „natürliche“
Exponentialfunktion die Basis 2 hat. Tatsächlich aber ist es nicht so
einfach, denn die Basis ist die sogenannte EULERsche Zahl
e ¼ 2; 718281828459045235360::: Die Zahl e 1) wurde nicht willkürlich festgelegt.
Vielmehr ist sie genau die Zahl, mit der man zahlreiche Naturgesetze
beschreiben kann.
Der Graph der Funktion mit der Gleichung
y ¼ e bx veranschaulicht für
b > 0 Zunahme, fürb< 0 Abnahme
von natürlichen Vorgängen.
Es genügt, wenn wir uns folgenden Näherungswert für e merken:
e ¼ 2;718
e ist — ähnlich wie p — keine periodische Dezimalzahl.
In der höheren Mathematik zählt die Exponentialfunktion x 7! e x zu den
wichtigsten Funktionen.
Einige historische Bemerkungen über Leonhard EULER:
Leonhard EULER (1707–1783) war der wahrscheinlich produktivste
Mathematiker, der je lebte. Das Verzeichnis seiner Werke umfasst rund 900
Titel, seine „Gesammelten Werke“, die seit 1907 herausgegeben werden,
umfassen derzeit mehr als 70 Bände und sind noch lange nicht abgeschlossen.
Leonhard EULER stammte aus einer Pastorenfamilie in Basel. Er studierte
bei Johann BERNOULLI (1667–1748), war von 1727–1741 an der Petersburger
Akademie der Wissenschaften, von 1741–1766 an der von
FRIEDRICH dem Großen gegründeten Berliner Akademie und ab 1766
wieder in Petersburg tätig. Außer mit zahlreichen Gebieten der Mathematik
beschäftigte sich EULER unter anderem mit Philosophie, Schiffsbau, Artillerie,
Astronomie, Kartografie, Optik und Musiktheorie. Beispielsweise
berechnete er für FRIEDRICH den Großen Lotterien und konstruierte Brunnen
mit Wasserspielen für den Schlosspark von Sanssouci. 1738 verlor
EULER nach einer schweren Infektion das Sehvermögen des rechten
Auges. 1771 erkrankte er auch am linken Auge schwer. Die letzten Jahre
seines Lebens war er beinahe blind.
Hier kamen ihm sein unfehlbares Gedächtnis und seine enorme Konzentrationsfähigkeit
zugute: Er diktierte seinen Gehilfen seine Arbeiten, die
sich vor allem durch ihre Klarheit und leichte Verständlichkeit auszeichneten.
Seine Lehrbücher prägten den noch heute üblichen Stil.
Aufgaben
84 Der Graph der folgenden durch ihre Funktionsgleichung gegebenen Funktion ist über der Definitionsmenge
D ¼fx 2 Rj 24x43g zu zeichnen:
a) y ¼ 3 x b) y ¼ 3 x c) y ¼ 3 jxj d) y ¼ 1
3 jxj
85 Text wie Aufgabe 84 fürD¼½ 3; 3Š:
a) y ¼ 4 x b) y ¼ 4 x c) y ¼ 4 jxj d) y ¼ p 1 ffiffiffi
jxj
n
4
86 Man berechne 1 þ 1 für a) n ¼ 1 b) n ¼ 10 c) n ¼ 99 d) n ¼ 1000 e) n ¼ 10000
n
n
Wir erkennen: Für wachsendes n nähert sich 1 þ 1 einer bestimmten Zahl. Diese Zahl heißt EULERsche
Zahl und wird mit dem Buchstaben e
n
bezeichnet.
1) e ist eine irrationale Zahl, d. h. sie kann nicht durch einen Bruch ganzer Zahlen
dargestellt werden. Ferner kann e auch nicht als n-te Wurzel ðn 2 N Þ einer
rationalen Zahl dargestellt werden. In diesem Zusammenhang sagen wir: e ist
eine transzendent irrationale Zahl.

Exponentialfunktion und Logarithmus(funktion) 33
87 Es sind die Funktionswerte y ¼ e x für nachstehende Argumente x zu berechnen, das Ergebnis ist auf 3
Dezimalstellen zu runden!
a) x ¼ 0;347 b) x ¼ 3;167 c) x ¼ 2;241 10 3 d) x ¼ 0;01273
88 Man zeichne a) x 7! e x b) x 7! e x für Š 2; 2½.
89 Nährstoffreiche Substanzen und feuchte Wärme von 20 C bis 37 C stellen günstige Lebensbedingungen
für Bakterien dar (z. B. Bakterien des Zahnbelags). Dabei vermehren sich diese durch Zweiteilung
etwa nach a) ¼ 20 min b) ¼ 0;5h c) ¼ 1h.
Man untersuche, wie viele solcher Lebewesen sich aus einer Bakterienzelle bei ungeänderten Umweltbedingungen
innerhalb eines Tages bilden können. (Gleitkommadarstellung!)
Anleitung: Die Vermehrung durch Zweiteilung führt auf folgende exponentielle Abhängigkeit der Anzahl
A: AðtÞ¼A 0 2 t ðA 0 .....Anzahl am Beobachtungsbeginn, AðtÞ .....Anzahl nach t Stunden).
Man beachte: ist jeweils die Zeit, nach der eine Verdopplung eintritt.
90 In einem # R ¼ 22 C warmen Zimmer liegt ein Grippekranker mit # K ¼ 38;5 CKörpertemperatur. Die
Prüfspitze des verwendeten Fieberthermometers erwärmt sich nach folgendem Gesetz:
# ¼ # K ð# K # R Þe t= ¼ 1;5 min, # in C, t in min
Auf welche Temperatur # ist das Thermometer nach a) 5 min b) 10 min angestiegen? Die Resultate sind
grafisch zu überprüfen.
91 Bei der embryonalen Entwicklung teilen sich die vorhandenen Zellen zunächst unabhängig voneinander.
Die Anzahl z der Zellen wächst dann nach dem Gesetz z ¼ 2 t , wobei t die Anzahl der Teilungsperioden
ist. Dieses Exponentialgesetz gilt aber nur bis etwa zur achten Teilungsperiode. Danach verändert sich
der Teilungsprozess und man kann dann nicht mehr von einem exponentiellen Wachstum sprechen.
Wie groß ist die Anzahl der Zellen nach jeder Teilungsperiode? t ¼ 1; ...; 8
92 Der Luftdruck p nimmt mit zunehmender Höhe (über Meeresspiegel) ab, und zwar nach der Formel
p ¼ p 0 e 0;13h (p in bar, h in km, p 0 ¼ 1;013 bar auf Meeresspiegelniveau; 1mbar = 1h Pa).
Wie groß sind demnach die durchschnittlichen Luftdruckwerte an folgenden geografischen Orten?
Ort
h in m
Bodensee (Vorarlberg) 396
Großglockner (Osttirol, Kärnten) 3797
Kufstein (Tirol) 499
Neusiedlersee (Burgenland) 115
Schneeberg (Niederösterreich) 2076
Sonnblick (Salzburg) 3105
Steyr (Oberösterreich) 310
Tamsweg (Salzburg) 1021
Turracher Höhe (Kärnten, Steiermark) 1783
Wien 171
Kilimandscharo (Tansania) 5895
Mt. Everest (Nepal) 8848

34 Exponentialfunktion und Logarithmus(funktion)
2. Was ist der „Logarithmus“?
log 3 5 ¼ x , 3 x ¼ 5
% - -
LINKS MITTE RECHTS
Logarithmus ¼ Exponent
Definition:
Jene Zahl x 2 R,für die a x ¼ b
ða 2 R þ nf1g; b 2 R þ Þ gilt, heißt
Logarithmus von b zur Basis a:
a x ¼ b , x ¼ log a b ¼ log a a x
Anhand der Definition und dem
Beispiel erkennen wir:
Das Potenzieren zur Basis a ist die
Umkehrung des Logarithmierens
zur Basis a
a log a x ¼ xfür alle x 2 R þ
Das Logarithmieren zur Basis a ist
die Umkehrung des Potenzierens
zur Basis a.
log a a x ¼ xfür alle x 2 R
Insbesondere gilt:
10 x ¼ b , x ¼ lg b
e x ¼ b , x ¼ ln b
3 x ¼ 5 — Wie groß ist x?
Eine schwierige Frage. Wir nehmen den Taschenrechner zur Hand und
versuchen dem x auf die Spur zu kommen, indem wir es jeweils zwischen
zwei rationale Zahlen einschließen:
1< x < 2 denn 3 1 ¼ 3 3 2 ¼ 9
1;4< x < 1;5 denn 3 1;4 ¼ 4;65554 3 1;5 ¼ 5;19615
1;42< x < 1;48 denn 3 1;42 ¼ 4;75896 3 1;48 ¼ 5;08323
Wir haben durch Probieren Intervalle gefunden, in denen x liegen muss.
Wir werden später einen Weg kennen lernen, wie man die Variable x in
Gleichungen dieser Art berechnen kann.
Offensichtlich besitzt eine Gleichung der Form a x ¼ bðb > 0Þ genau eine
Lösung x 2 R. Diese Zahl x heißt der „Logarithmus von b zur Basis a“.
Man schreibt x ¼ log a b.
Bezeichnungen: a heißt Basis, b heißt Numerus 1) , x nennt man Logarithmus.
Den Logarithmus berechnen heißt den Exponenten einer Potenz
bestimmen.
Beispiel:
Die folgenden Logarithmen sind mit Hilfe der Äquivalenz
x ¼ log a b , a x ¼ b zu bestimmen:
a) log 3 9 ¼ ? b) log 4 64 ¼ ? c) log 1
7 49 ¼ ? d) log 0;5 1
32 ¼ ?
Lösung:
a) log 3 9 ¼ 2, weil 3 2 ¼ 9 b) log 4 64 ¼ 3, weil 4 3 ¼ 64
c) log 1
7 49 ¼ 2, weil 7 2 ¼ 1 d) log 1
49
0;5 32 ¼ 5, weil 1 5¼
1
2 32
Das Logarithmieren ist eine Rechenoperation 3. Stufe.
Von besonderer Bedeutung sind die Logarithmen zur Basis 10. Sie werden
als dekadische Logarithmen, Zehnerlogarithmen oder BRIGGSsche
Logarithmen 2) bezeichnet. Wir vereinbaren für die dekadischen Logarithmen
die abkürzende Bezeichnung lg u („logarithmus generalis“) statt
log 10 u zu verwenden.
Nicht weniger wichtig sind die Logarithmen zur Basis e. Die Logarithmen
zur Basis e ¼ 2;718 ... heißen natürliche Logarithmen. Statt log e a
schreibt man ln a („logarithmus naturalis“).
Zur Bestimmung der Logarithmen verwendete man früher Logarithmentafeln
3) . Heute besitzt fast jeder Taschenrechner eine „Logarithmustaste“
bzw. eine „Logarithmusfunktion“.
Informieren Sie sich durch die Bedienungsanleitung Ihres Taschenrechners,
wie man den dekadischen und den natürlichen Logarithmus
bestimmt und wie man umgekehrt jeweils den Numerus ermittelt.
Anschließend sind die nachstehenden Beispiele mit Hilfe des Taschenrechners
nachzuvollziehen:
(1) lg3481 ¼ 3;5417 (2) ln 17 ¼ 2;8332
(3) 3;2534 ¼ lg 1792;25 (4) 1;9867 ¼ ln 7;2914
1) Mehrzahl: Numeri
2) Der englische Mathematiker Henry BRIGGS (1561–1630) führte 1617 die
Zehnerlogarithmen ein.
3) Siehe Seite 35.

Exponentialfunktion und Logarithmus(funktion) 35
Im 17. Jahrhundert erforderte die aufstrebende Seefahrt, dass für Navigationszwecke
komplizierte Berechnungen mit großer Genauigkeit in kurzer
Zeit durchgeführt wurden. So kam es zur Erfindung der Logarithmen, über
die der französische Mathematiker Marquis Pierre-Simon DE LAPLACE
(1749—1827) sagte: „Die Erfindung der Logarithmen kürzt monatelang
währende Berechnungen bis auf einige Tage ab und verdoppelt dadurch
sozusagen das Leben (der Rechner)“. Die dekadischen Logarithmen
wurden auf eine bestimmte Anzahl von Dezimalstellen berechnet 1) und in
Tabellen, sogenannten Logarithmentafeln festgehalten.
Eine Seite einer dekadischen Logarithmentafel:
Durch eine uns heute umständlich und zeitintensiv erscheinende
Vorgangsweise wurden zu den Numeri die zugehörigen dekadischen
Logarithmen aufgesucht und mit letzteren die entsprechenden — um eine
Stufe erniedrigten — Rechenoperationen durchgeführt. Auf dem gleichen
Prinzip (der Vereinfachung des praktischen Rechnens durch Erniedrigung
der Rechenstufe) beruht der logarithmische Rechenschieber. Bis vor einigen
Jahren gab es zum Rechenschieber und zur Logarithmentafel keine
Alternative. Erst durch die — mit der Weltraumtechnik in engem Zusammenhang
stehende — Erfindung der integrierten Schaltkreise wurde die
billige Massenproduktion von elektronischen Taschenrechnern ermöglicht.
Mit Hilfe des Taschenrechners wird die Rechenarbeit entscheidend reduziert.
Das Rechnen mit Logarithmen hat daher stark an Bedeutung verloren.
Aufgaben
1
93 a) log 2 64 ¼ ? b) log 3 243 ¼ ? c) log 4 8 ¼ ? d) log 1
5
pffiffiffiffiffiffi
¼ ?
125
94 a) log 1 0;5=? b) log 1 27 ¼ ? c) log 1
1 5p ffiffiffiffi ¼ ? d) log
3p ffiffiffiffiffi
1 25 ¼ ?
2
3
4 16
5
95 a) log 4
2
3 9 ¼ ? b) log 4 1 ¼ ? c) log 64
7 ¼ ? d) log 3 p1ffiffiffiffiffi
¼ ?
5
8 49 10 0;3
n
96 log 2 bfürb2 1; 2; 0;5; 1
16 ; p ffiffiffi ffiffiffi
o
2 ;
3p
4 ; 1
0;125 ; p ffiffiffiffiffiffi 1 ; 1 ffiffi
128 7p ; ffiffiffiffiffiffiffiffiffi 1
4
3p
1024
n
97 log 5 bfürb2 5; 1 5 ; 25; 1; 1
625 ; 0;04; p ffiffiffi ffiffiffiffiffiffiffiffi
5 ;
4p ffiffiffi o
125;
3p
5 ; 1
7p ffiffi
a log a x ¼ x; x 2 R þ
5
n
98 log 10 bfürb2 10; 1; 100; 1000; 10 6 ffiffiffiffiffi
; 0;01; 0;1;
4p ffiffiffiffiffiffiffiffi o
10 ;
3p
100; ffiffiffiffiffiffiffiffiffi
1
4p
1000
Bei den Aufgaben 99 bis 106 ist jeweils die Variable x zu berechnen!
99 a) log x 125 ¼ 3 b) log x 216 ¼ 3 c) log x
1
8 ¼ 3 d) log x 64 ¼ 3
100 a) log x
1
256 ¼ 8 b) log x 3 4 ¼ 1 c) log x 256 ¼ 2 d) log x 128 ¼ 7
101 a) log 2 x ¼ 10 b) log 3 x ¼ 2 c) log 4 x ¼ 1 2
d) log 5 x ¼ 3
102 a) log 0;2 x ¼ 1 b) log 6 x ¼ 3 c) log 1;125 x ¼ 1 d) log
7
3
1;5 x ¼ 2
103 a) x ¼ lg 43;53 b) lg x ¼ 1;5 c) x ¼ lg 0;1 d) lg x ¼ 3
104 a) lg x ¼ 1;2 b) x ¼ lg 25 c) lg x ¼ 0;1 d) lg x ¼ 1;105
105 a) x ¼ ln 54;52 b) ln x ¼ 3;9 c) x ¼ ln 0;2 d) ln x ¼ 5
106 a) ln x ¼ 173;5 b) x ¼ ln 49 c) ln x ¼ 1;4 d) ln x ¼ 5;123
1) Allgemein gültige Verfahren zum Berechnen von Logarithmen erfordern tiefe
mathematische Kenntnisse, auf die hier nicht eingegangen werden kann.

36 Exponentialfunktion und Logarithmus(funktion)
Es gilt:
log a a ¼ 1; weil a 1 ¼ a
log a 1 ¼ 0; weil a 0 ¼ 1
log a a n ¼ n; weil a n ¼ a n
1 Der Logarithmus eines Produkts
ist gleich der Summe der Logarithmen
der Faktoren.
2 Der Logarithmus eines Quotienten
ist gleich der Differenz aus
dem Logarithmus des Dividenden
und dem des Divisors.
3 Der Logarithmus einer Potenz ist
gleich dem Produkt aus ihrem
Exponenten und dem Logarithmus
der Potenzbasis.
4 Der Logarithmus einer Wurzel ist
gleich dem Quotienten aus dem
Logarithmus des Radikanden
und dem Wurzelexponenten.
3. Rechengesetze für Logarithmen
Für das Rechnen mit Logarithmen gelten nämlich folgende Rechengesetze:
1 log a ðu vÞ¼log a u þ log a v ðu > 0; v > 0; a > 0; a 6¼ 1Þ
z. B.: log 7 ð5 6 7Þ¼log 7 5 þ log 7 6 þ log 7 7 ¼ log 7 5 þ log 7 6 þ 1
2 log u
a v ¼ log a u log a v ðu > 0; v > 0; a > 0; a 6¼ 1Þ
z. B.: lg0;01 ¼ lg 1 ¼ lg 1 lg100 ¼ 0 2 ¼ 2
100
3 log a u r ¼ r log a u ðu > 0; a > 0; a 6¼ 1; r 2 RÞ
z. B.: log 3 3¼
3 3 log3 3 ¼ 3ðlog
5
5
3 3 log 3 5Þ¼3ð1 log 3 5Þ
4 log np ffiffiffi
a u ¼ 1
n log a u ðu > 0; a > 0; a 6¼ 1; n 2 N Þ
rffiffiffiffiffiffiffiffiffiffiffiffi
3 3
7
z. B.: log 6
a ¼ log 6 7
7 a ¼ 3 7 7 log a 6 7 ¼ 3 7 ðlog a 6 log a 7Þ
Durch Anwendung dieser Rechengesetze tritt
— an Stelle der Multiplikation die Addition,
— an Stelle der Division die Subtraktion,
— an Stelle des Potenzierens die Multiplikation und
— an Stelle des Wurzelziehens die Division.
Somit werden die Rechenoperationen der 3. Stufe auf Rechenoperationen
der 2. Stufe, die der 2. Stufe auf die der 1. Stufe zurückgeführt.
Beispiel:
Die folgenden Terme 1) sind mit Hilfe der Rechengesetze für Logarithmen (so weit wie möglich) additiv zu
zerlegen:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p
a) log a2 pb ffiffi
4
b) log a2 b 2
3
c) log 6x 3 x 2
c
10x
x 2 9
Lösung:
a) log a2 pb ffiffi
4
¼ 2log a þ 4 logb 1
c
2 log c
b) log a2 b 2 ða þ bÞða
¼ log bÞ ¼ logða þ bÞþlogða bÞ log2 log 5 logx
10x
2 5x
Man beachte: logða þ bÞ 6¼ log a þ log b (häufiger Fehler)!
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p
3 6x
c) log
3 x 2
¼ log 6x3 ðx 2Þ 1 1 2 3
h
i
¼
1
x 2 9
ðx þ 3Þðx 3Þ 3 log 6x3 þ 1 logðx 2Þ logðx þ 3Þ logðx 3Þ ¼
2
h
i
¼ 1 3 log 2 þ log 3 þ 3 log x þ 1 logðx 2Þ logðx þ 3Þ logðx 3Þ ¼
2
¼ 1 3 log 2 þ 1 3 log 3 þ logx þ 1 6 logðx 2Þ 1
3 logðx þ 3Þ 1 logðx 3Þ
3
1) Da es gleichgültig ist, welche Basis aus R þ nf1g dem Logarithmus zu Grunde
liegt, schreiben wir bei den Beispielen und Aufgaben statt „log a “ nur „log“.
Ferner vereinbaren wir, dass alle auftretenden Variablen so durch reelle Zahlen
ersetzt werden, dass die zugehörigen Logarithmen definiert sind.

Exponentialfunktion und Logarithmus(funktion) 37
Beispiel:
Die nachstehenden algebraischen Summen sind in den Logarithmus eines einzigen Terms zu verwandeln:
1
a) log u þ log
h
v ðlog w þ log xÞ
i
b) 3 log a logða bÞ
3
c) 4 log x 1
5 3 logðx yÞ þ 1 logðx þ yÞ
4
Lösung:
a) log u þ log v ðlog w þ log xÞ¼log uv
wx
b) 3 log a 1
3 logða bÞ¼log a3 logða bÞ 1 3 ¼ log a
3p ffiffiffiffiffiffiffiffiffi
3
a b
h
i
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
c) 4 log x 1
5 3logðx yÞ þ 1 logðx þ yÞ ¼ log x 4 5
log ðx yÞ 3 4p ffiffiffiffiffiffiffiffiffiffiffiffi x þ y ¼ log pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 4
4 5
ðx yÞ 3 4p x þ y
Nachdem wir die Rechengesetze für Logarithmen bereits erfolgreich angewendet
haben, wollen wir nun überlegen, warum diese Gesetze gelten.
Betrachten wir z. B. das Rechengesetz 1 (vgl. Außenspalte)
Wir haben den Logarithmus als Exponent einer Potenz definiert. Daher gilt
m ¼ log a u , u ¼ a m und n ¼ log a v , v ¼ a n .
Wir wenden die Rechenregel für die Multiplikation von Potenzen (vgl.
Außenspalte) an und erhalten u v ¼ a m a n ¼ a m þ n , m þ n ¼ log a ðu vÞ.
Die Gültigkeit der anderen Rechengesetze lässt sich mit ähnlichen Überlegungen
zeigen.
Aufgaben
1 log a ðu vÞ¼log a u þ log a v
Potenzen mit gleicher Basis werden
multipliziert, indem man die Basis
mit der Summe der Exponenten
potenziert:
a m a n ¼ a m þ n
Bei den folgenden Aufgaben sind die gegebenen Terme mit Hilfe der Rechengesetze für Logarithmen (so weit
wie möglich) additiv zu zerlegen:
107 a) log (abcd) b) log ab
cd
108 a) log 5a 12 3p ffiffiffi
b
b) log 12a 5 3p ffiffiffi
b
c) log a4 b 3
c 2
qffiffiffiffiffiffiffiffi
4
c) log a 3 b
c
pffiffi
a
d) log
b 5 c
rffiffiffiffiffiffiffi
d) log
xy p ffiffi
2 c
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
109 a) logða bÞ b) logða 4 b 4 Þ 3 c) log a2 þ b 2
d) log 16a 2 25b 2
a 2 b 2 2a
Bei den folgenden Aufgaben sind die gegebenen algebraischen Summen in den Logarithmus eines einzigen
Terms zu verwandeln:
110 a) log a log b þ log c b) log 3 þ log 4 log 2
111 a) 2 log a 3 log b þ 5 log c b) 2 log 3 þ 3 log 4 5 log 2
112 a) log 7 þ log a
1
2 log b þ 2log c b) log a 1
logðb cÞ
2
113 a) 2 log a log b þ 1 2 log x 3
5 log y b) 3 log x log y þ 3 4 log a 1
2 log b
114 a) 1
5 2 log x þ 6 5 log b 3
5 log 2 1
5 log a b) 1
11 3log a þ 5 4 log y 3
4 log 3 1
4 log x
h
i
115 a) 1
5 log x logðx þ yÞ þ3 log y 4 log xy b) 1 log a þ logða bÞ 2 log b þ 3 log ab
7 6 ½
Š

38 Exponentialfunktion und Logarithmus(funktion)
4. Logarithmusfunktionen
Wer kann sich möglichst viele der nebenstehend fotografierten Artikel
merken? 5 Minuten stehen zur Verfügung, dann ist das Buch wegzulegen
und alle Produkte, die im Gedächtnis haften geblieben sind, werden aufgeschrieben.
Gleichgültig wie gut oder schlecht man dabei abschneidet:
Umso weniger Waren man nennen kann, desto länger wird der Zeitpunkt
des Lernens zurückliegen.
Durch Experimente haben Psychologen festgestellt, dass die Anzahl der
erinnerten Objekte etwa logarithmisch mit der Zeit des Lernvorgangs
zunimmt. Die Veranschaulichung dieses Zusammenhangs erfolgt durch
eine sogenannte Logarithmusfunktion. Über Graph und Eigenschaften
der Logarithmusfunktion wollen wir in diesem Abschnitt sprechen.
Beispiele für Logarithmusfunktionen: x 7! log 2 x, x 7! lg x, x 7! ln x usw.
Definition:
Logarithmusfunktionen sind
Funktionen, die durch eine Funktionsgleichung
y ¼ log a x
ða 2 R þ nf1g; x 2 R þ Þ dargestellt
werden können.
Darstellung der Funktion x7!3 x und
ihrer Umkehrfunktion — vgl. nebenstehendes
Beispiel.
-
y
6-
y = 3 x
5-
4-
3-
2-
1-
-
y = x
y = log 3 x
-
-
-
-
-
–1 1 2 3 4 5 6
–1-
Die logarithmische Funktion
x 7! log a x ist die Umkehrfunktion
der Exponentialfunktion x 7! a x .
Aufgaben
x
Beispiel:
Zu der durch ihre Funktionsgleichung y ¼ 3 x gegebenen Funktion ist
die Umkehrfunktion zu berechnen.
Lösung:
Zur Wiederholung: Definitionsmenge und Wertemenge tauschen bei
der Umkehrung einer Funktion ihre Rollen, d.h. die Variablen x und y
sind zu tauschen. Die neue Gleichung wird anschließend — wenn
immer das möglich ist — nach y gelöst.
y ¼ 3 x ) Umkehrung: x ¼ 3 y
Um in der Gleichung x ¼ 3 y die Variable y explizit auszudrücken,
logarithmieren wir beide Seiten der Gleichung (vgl. Seite 40) und
wenden die Definition des Logarithmus an:
x ¼ 3 y , log 3 x ¼ log 3 3 y , log 3 x ¼ y log 3 3 log 3 3 ¼ 1 (!)
y ¼ log 3 x
Wir erkennen: Die logarithmische Funktion x 7! log 3 x ist die Umkehrfunktion
der Exponentialfunktion x 7! 3 x !
Einige Eigenschaften der Funktion x 7! log a x ða 2 R þ nf1g; x 2 R þ Þ:
1 Definitionsmenge D ¼ R þ
2 Wertemenge W ¼ R
3 Die y-Achse ist Asymptote.
4 x 7! log a x geht immer durch den Punkt Pð1 j 0Þ.
5 x 7! log a xfüra> 1 ist streng monoton wachsend, für0< a < 1 streng
monoton fallend.
6 x 7! log a x ist die Umkehrfunktion von x 7! a x .
116 Zu der durch ihre Funktionsgleichung a) y ¼ 2 x b) y ¼ 2 x c) y ¼ 5 x d) y ¼ 5 x gegebenen Funktion ist
die Umkehrfunktion zu berechnen!
117 Der Graph von a) y ¼ log 3 x b) y ¼ log 7 x ist durch Spiegelung des Graphen der zugehörigen Exponentialfunktion
an der Geraden x 7! x zu konstruieren.
118 Die logarithmische Funktion a) x 7! log 2 x b) x 7! ln 3x ist grafisch darzustellen.
119 Die folgenden natürlichen Logarithmusfunktionen sind grafisch darzustellen:
a) x 7! ln x b) x 7! ln 2x c) x 7! ln x d) x 7! ln 3x

Exponentialfunktion und Logarithmus(funktion) 39
5. Exponentialgleichungen
Exponentialgleichungen sind Gleichungen, bei denen die Variable im
Exponenten vorkommt.
Beispiele für Exponentialgleichungen: 2 x ¼ 2 5 , e xþ1 ¼ 4, 5 xþ2 ¼ 5 xþ2 usw.
Exponentialgleichungen mit Potenzen gleicher Basis a fðxÞ ¼ a gðxÞ
können einfach gelöst werden.
Beispiel:
Die Gleichung 23x
16 ¼ 2x ist in R zu lösen!
128
Lösung:
2 3x
2 4 ¼ 2x
2 7 , 23x 4 ¼ 2 x 7
3x 4 ¼ x 7 , 2x ¼ 3 , x ¼ 3 2
Potenzen mit gleicher Basis können
nur dann gleich sein, wenn auch ihre
Exponenten gleich sind:
a fðxÞ ¼ a gðxÞ , fðxÞ¼gðxÞ
ða 2 R þ nf1gÞ
z. B.: 3 x ¼ 3 4 , x ¼ 4
Probe:
T 3 L ¼ 2 9 2
2 16 ¼ p 1 ffiffiffiffi 1
¼ p ffiffi ¼ 1 p ffiffi
16 2 9 16 16 2 256 2
T 3 R ¼ 2 3 2
2 128 ¼ 1 p ffiffiffiffi ¼ 1 p ffiffi ¼ 1 p ffiffi
128 2 3 128 2 2 256 2
n o
Somit gilt: L ¼ 3
2
T L ¼ T R (w)
Exponentialgleichungen
mit verschiedenen Basen, aber gleichen Exponenten
a fðxÞ ¼ b fðxÞ können durch folgende Überlegung auf den obigen
Fall zurückgeführt werden:
fðxÞ¼
a fðxÞ ¼ b fðxÞ , afðxÞ
b ¼ 1 , a a 0,
fðxÞ¼0
fðxÞ b b
Beispiel:
2 2x 7 27 ¼ 3 2x 4 ist in N zu lösen!
Lösung:
2 2x 7 27 ¼ 3 2x 4
2 2x 7 3 3 ¼ 3 2x 4
2 2x 7 ¼ 3 2x 7
2x 7 ¼ 0
2x ¼ 7
x ¼ 7 2
Probe:
T 7 L ¼ 2 2 7 7
2 27 ¼ 2 0 27 ¼ 27
2
T 7 R ¼ 3 2 7 4
2 ¼ 3 3 ¼ 27
2
T L ¼ T R (w)
Im Hinblick auf die Grundmenge N gilt: L ¼fg
a fðxÞ ¼ b fðxÞ , fðxÞ¼0
ða; b 2 R þ ; a 6¼ bÞ
z. B.: 7 x ¼ 5 x , x ¼ 0

40 Exponentialfunktion und Logarithmus(funktion)
Eine Gleichung geht in eine äquivalente
Gleichung über, wenn
man beide Seiten der Gleichung
logarithmiert.
Logarithmieren ist eine Äquivalenzumformung,
da eine eindeutige
Umkehrung der Logarithmusfunktion
gegeben ist. (Im
Gegensatz dazu gibt es zur
quadratischen Funktion keine
eindeutige Umkehrung, sodass
Quadrieren keine Äquivalenzumformung
ist.)
Um Exponentialgleichungen zu lösen, die verschiedene Basen und
verschiedene Exponenten haben (z. B.: 2 xþ3 ¼ 5 x ), müssen beide Seiten
der Gleichung logarithmiert werden. Dies zeigen die nächsten Beispiele.
Beispiel:
Man löse in 3 x ¼ 4inR!
Lösung:
3 x ¼ 4 , lg 3 x ¼ lg 4 , x lg 3 ¼ lg4 $ x ¼ lg4
lg3
x 0;60206
0;47712 ) x 1;2619
Probe:
T L ð1;2619Þ¼3 1;2619 4
T R ¼ 4 T L ¼ T R (w) Es gilt: L ¼f1;2619g
Beispiel:
7 2x 4 x 2 ¼ 11 x ist in R zu lösen!
Lösung:
7 2x 4 x 2 ¼ 11 x , 2x lg 7 þðx 2Þ lg4 ¼ x lg11
2x lg 7 þ x lg 4 x lg 11 ¼ 2lg4
xð2lg7þ lg4 lg 11Þ¼2lg4
2lg4
x ¼
2lg7þlg 4 lg 11
x 1;20412
1;25086
x 0;96263
Probe:
T L ð0;96263Þ¼7 1;92526 4 1;03737 10;057
T R ð0;96263Þ¼11 0;96263 10;057
T L ¼ T R (w)
Es gilt:
L ¼f0;96263g
Aufgaben
Bei den folgenden Aufgaben ist die Lösungsmenge in R zu ermitteln!
120 a) 3 x ¼ 27 2 b) 2 2x ¼ 256 c) 7 3ðx 12Þ ¼ 1 d) 9 xþ3 ¼ 1
27
121 a) 5 3x þ 2
5 ¼ x 1 53 b) 75x þ 3
7 ¼ 1
c) 2 x 5 4 3xþ7 ¼ 16 4 d) 32x 1
¼ 27 3xþ13
2 þ 3x 7 2 5x 9
122 a) 2 x ¼ 3 b) 3 x ¼ 2 c) 3 x 1 ¼ 5 d) 5 xþ1 ¼ 3
x
123 a) 3 xþ1 ¼ 1
b) 9 xþ1 ¼ 81 c) 2 1 x ¼ 64 d) 4 2¼
16
27
25 625
124 a) 0;16 4 2 4x ¼ 5 2x 1 b) 5 xþ2 7 2x 0;5 x ¼ 5 x 7 2x 3
125 a) 2 3x 3 4 2xþ2 8 xþ1 ¼ 16 b) 2 2xþ3 4 1 2x ¼ 8 2xþ2

Exponentialfunktion und Logarithmus(funktion) 41
6. Logarithmische Gleichungen
Logarithmische Gleichungen sind Gleichungen, bei denen die Variable im
Numerus von einem Logarithmus vorkommt.
Beispiele für logarithmische Gleichungen: lgðx þ 100Þ¼0;30103,
log 3 10 log 3 5 ¼ log 3 x, lnðx 3 4Þ¼3lnðx 2Þ usw.
Durch Anwendung der Rechengesetze für Logarithmen versuchen wir, die
Gleichung auf die Form log a fðxÞ¼log a gðxÞ zu bringen.
Beispiel:
lgðx 2Þ lg x ¼ lgðx þ 3Þ lgðx þ 10Þ ist in R zu lösen!
Lösung:
Wir wenden das Rechengesetz 2 für Logarithmen an:
lg x 2
x
¼ lg x þ 3
x þ 10 , x 2 ¼ x þ 3
x x þ 10
ðx 2Þðx þ 10Þ¼xðx þ 3Þ
x 2 þ 8x 20 ¼ x 2 þ 3x
5x ¼ 20
x ¼ 4
Probe:
T L ð4Þ¼lg 2 lg 4 ¼ lg 0;5
T R ð4Þ¼lg 7 lg 14 ¼ lg 0;5 T L ¼ T R (w) ) L ¼f4g
Logarithmen mit gleicher Basis
können nur dann gleich sein, wenn
auch ihre Numeri gleich sind:
log a fðxÞ¼log a gðxÞ,fðxÞ¼gðxÞ
ða > 1; fðxÞ > 0; gðxÞ > 0Þ
2 log a u log a v ¼ log a
u
v
Wir wissen von der Definition des Logarithmus, dass die obige Gleichung
nur Sinn hat, wenn
(1) x 2 > 0 ) x > 2,
(2) x > 0,
(3) x þ 3 > 0 ) x > 3 und
(4) x þ 10 > 0 ) x > 10.
Daher ist die Gleichung nur fürx> 2 definiert.) D ¼fx j x 2 R ^ x > 2g
Beispiel:
ln 5x 5 4ln5x¼ ln 5 ist in R zu lösen!
Lösung:
Es ist als Grundmenge gegeben. Es gilt: D ¼ R þ
Wir wenden die Rechengesetze 2 und 3 für Logarithmen an:
ln 5x 5 4ln5x¼ ln 5
ln 5x5 ¼ ln 5
ð5xÞ 4
5x 5
5 4 x ¼ 5 4 x ¼ 5 4 ¼ 625
Probe:
T L ð625Þ¼33;798 32;189 ¼ 1;609
T R ð625Þ¼1;609 T L ¼ T R (w) ) L ¼f625g
2 log a u log a v ¼ log a
u
v
3 r log a u ¼ log a u r
Man überlege, warum die nebenstehende
logarithmische Gleichung für
x 2 R þ definiert ist.

42 Exponentialfunktion und Logarithmus(funktion)
Aufgaben
Bei den folgenden Aufgaben ist die Lösungsmenge in R zu ermitteln!
126 a) lgðx þ 3Þþlg2x ¼ lgðx þ 9Þþlgð2x 4Þ b) lnð3x 5Þþlnð15 8xÞ¼lnð6x 11Þþlnð7 4xÞ
127 a) lgðx þ 2Þ lgð3x 1Þ¼lgðx þ 5Þ lgð3x þ 1Þ b) lgðx þ 30Þ lgðx þ 10Þ¼lgðx þ 60Þ lgðx þ 20Þ
128 lgð5x 1Þ 0;60206 ¼ 0;47712 lg7 þ lgð9x þ 1Þ lg 3
129 a) lg x 5 lg x 2 ¼ lg 8 b) lg x 3 lg x 2 ¼ 2;38561
130 a) 5lgx 2lgx 2 ¼ 1;20412 b) 3lgx 5 5lgx 2 ¼ 1;50515
131 a) x lg 10 ¼ lg 100 b) x lg3 ¼ 0;95424 c) x lg 18 ¼ 17512
132 a) lnð5x þ 12Þþlnð5x 12Þ¼ln 81 b) lgð7x þ 2Þ lg 60 ¼ lgð7x 2Þ
133 a) lgð2x þ 5Þþ2 ¼ 2;9542 lgð2x þ 5Þ b) lgð3x þ 12Þþ0;60206 ¼ 2 lgð3x 12Þ
134 a) x lg x ¼ 1 b) x lg x ¼ 10 c) x lg x ¼ 10000
135 a) lgðx 1Þþlgð2 xÞ¼lgðx þ 2Þþlgðx 5Þ b) lgðx 3Þ lgð2x þ 7Þ¼lgð3x þ 1Þ lgðx 5Þ
136 a) lgðx þ 3Þ lgð3x 5Þ¼lgðx 1Þ lgð2x 6Þ b) lgðx 1Þþlgðx þ 2Þ¼lgð2x þ 1Þþlgðx 2Þ
137 a) 2lnðx þ 3Þ 3lnðx þ 2Þþlnðx þ 1Þ¼0 b) lgðx 3Þ¼0;90309 þ lgx lgðx þ 3Þ
Jost BÜRGI
John NAPIER
Einige historische Bemerkungen über Logarithmen:
Eine Methode, die jahrhundertelang in Verwendung stand, war das Rechnen
mit Logarithmen, die zunächst nicht als Exponenten von Potenzen
betrachtet wurden. Um einen brauchbaren Algorithmus zu erhalten,
musste man Logarithmentafeln mit geringer Schrittweite aufstellen. Der
Schweizer Uhrmacher Jost BÜRGI (1552–1632) entwickelte bereits Ende
des 16. Jahrhunderts als Hofastronom in Prag sogenannte „Progress-
Tabulen“. Johannes KEPLER (1571–1630) erkannte die Nützlichkeit
dieses neuen Hilfsmittels und überredete BÜRGI, diese zu drucken. In den
Wirren des 30-jährigen Krieges gingen die meisten Exemplare der 1620
erschienenen Tabellen verloren. Unabhängig von BÜRGI stellte der schottische
Baron John NAPIER (NEPER) (1550–1617) gleichfalls Logarithmentafeln
auf, die 1614 mit dem Titel „Mirifici Logarithmorum...“ in Edinburgh
veröffentlicht und rasch bekannt wurden. 1616 wurden sie ins Englische
übersetzt, 1617 lernte KEPLER sie kennen und war begeistert.
Sowohl BÜRGI als auch NAPIER nahmen als Basis der Logarithmen
Zahlen, die e (der Basis der natürlichen Logarithmen) bzw. 1=e nahe sind.
Als der englische Professor der Geometrie Henry BRIGGS (1560–1630)
von den NAPIERschen Logarithmen erfuhr, kontaktierte er NAPIER und
schlug ihm vor, als Basis 10 zu nehmen, und gemeinsam mit NAPIER
berechnete BRIGGS solche Tabellen, die nach dem Tod NAPIERS veröffentlicht
wurden. Die BRIGGSschen Tabellen wurden auf 14 Dezimalstellen
genau berechnet. Ende des 17. Jahrunderts erkannte man, dass die Logarithmusfunktion
die Umkehrfunktion der Exponentialfunktion ist. Wer heute
auf Knopfdruck mit dem Taschenrechner bzw. Taschencomputer den
Logarithmus einer Zahl berechnet, sollte sich wenigstens ungefähr vorstellen
können, was in seiner „Black Box“ vorgeht.