21 Knickbeanspruchung - Umwelt-Campus Birkenfeld

Umwelt-Campus Birkenfeld
Technische Mechanik III
21. Knickbeanspruchung
20. Kombinierte Beanspruchung
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
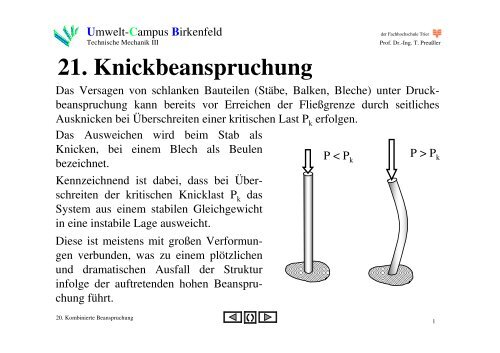
Das Versagen von schlanken Bauteilen (Stäbe, Balken, Bleche) unter Druckbeanspruchung
kann bereits vor Erreichen der Fließgrenze durch seitliches
Ausknicken bei Überschreiten einer kritischen Last P k erfolgen.
Das Ausweichen wird beim Stab als
Knicken, bei einem Blech als Beulen
P < P
bezeichnet.
k
P > P k
Kennzeichnend ist dabei, dass bei Überschreiten
der kritischen Knicklast P k das
System aus einem stabilen Gleichgewicht
in eine instabile Lage ausweicht.
Diese ist meistens mit großen Verformungen
verbunden, was zu einem plötzlichen
und dramatischen Ausfall der Struktur
infolge der auftretenden hohen Beanspruchung
führt.
1

Umwelt-Campus Birkenfeld
Technische Mechanik III
21.1 Kritische Last
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Die beim Knicken auftretende Instabilität wird anhand zweier gelenkig
miteinander verbundener starren Stäben hergeleitet, die axial belastet und seitlich
durch eine Feder gestützt werden.
Für das Kräftegleichgewicht am verformten System muss die Federkraft gleich
oder größer sein als die horizontalen Kraftkomponenten
F ≥ Px = 2⋅P⋅tanϕ
Mit F = k·∆y und ∆y = L/2·tanϕ folgt
L
2P⋅tanϕ ≤ k⋅
tanϕ
2
und damit die Bedingung
k⋅L
P ≤
4
für eine stabile Gleichgewichtslage.
∆y
ϕ
P
L/2
k
L/2
P·tanϕ
P
P
F
P·tanϕ
20. Kombinierte Beanspruchung
2

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Der Maximalwert von P wird als kritische Knicklast bezeichnet
P k
k⋅L
=
4
Für P < P k ist das System im stabilen Gleichgewicht, d. h. die Federkraft ist ausreichend,
um bei einer kleinen Auslenkung die Stäbe wieder in die Ausgangsposition
zu bringen.
Für P > P k wird das System instabil, d. h. die Stäbe
weichen zur Seite aus. Eine neue Gleichgewichtslage
wird erst bei großer Verformung am Anschlag
der Feder erreicht.
Ist P = P k , so befindet sich das System im indifferenten
Gleichgewicht, eine kleine Auslenkung bewirkt
eine horizontale Verschiebung des Gelenks,
ohne das dieses in die Ausgangsposition zurückkehrt.
P
Verzweigungspunkt
-ϕP k
ϕ
20. Kombinierte Beanspruchung
3

Umwelt-Campus Birkenfeld
Technische Mechanik III
21.2 Ideal belastete Druckstäbe
M b
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Betrachtet wird ein gerader, idealer Druckstab, der im Lastangriffspunkt geführt
und an seinem anderen Ende durch ein Gelenk gelagert ist.
Weicht der Stab unter der Wirkung der Druckkraft P seitlich aus, wirkt zusätzlich
zur Normalkraft das Lastmoment
P
P
M = P⋅
y
Nach der Biegetheorie wird das Biegemoment
durch die linearisierte Differential-
x
y
gleichung der Biegelinie beschrieben:
= −EI
⋅ y''
L
y
Hierbei ist y´´ die zweite Ableitung der
Durchbiegung, E ist der Elastizitätsmodul
und I das axiale Flächenträgheitsmoment.
Das Produkt E·I wird als Biegesteifigkeit
bezeichnet.
20. Kombinierte Beanspruchung
4

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Im einer stabilen Lage steht das Moment infolge der Last und das Biegemoment
im Gleichgewicht, es gilt M = M b und somit
oder
P⋅
y = −EI
⋅ y''
EI ⋅ y' ' + P⋅
y = 0
Dieser Ausdruck stellt eine homogene Differentialgleichung 2. Ordnung mit
konstanten Koeffizienten dar. Setzt man ω 2 = P/EI, lässt sich die Differentialgleichung
in die Form
2
y''
+ ω ⋅ y = 0
bringen, die auch bei Schwingungsproblemen auftritt. Es handelt sich um ein
sog. Eigenwertproblem. Die allgemeine (reelle) Lösung lautet:
y = C1 ⋅sin( ω⋅
x)
+ C2
⋅cos(
ω ⋅ x)
mit der Eigenkreisfrequenz ω und den Integrationskonstanten C 1 und C 2 , die an
die Randbedingungen noch anzupassen sind.
20. Kombinierte Beanspruchung
5

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Für das betrachtete System gilt, dass die seitliche Auslenkungen in den starren
Lagern gleich Null sein müssen:
y( x = 0) = 0
y( x = L)
= 0
= C1 ⋅sin( ω ⋅0)
+ C2
⋅cos(
ω ⋅0)
= 0 = 1
⇒ C 2
= 0
Die zweite Gleichung besitzt mehrer Lösungen. Für C 1 = 0 erhält man den
trivialen Fall, dass der Stab unter der Wirkung der Druckkraft nicht ausgelenkt
wird. Es handelt sich um die statische Gleichgewichtslage.
Ist C 1 ≠ 0, wird die Gleichung erfüllt, wenn
sin( ω ⋅ L)
=
0
⇒ C1 ⋅sin(
ω⋅
L)
= 0
bzw.
ω ⋅ L =
P
⋅ L = n⋅π
EI
für n = 0, 1, 2, ...
gilt.
20. Kombinierte Beanspruchung
6

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Aufgelöst nach der Druckkraft ergibt sich
2 2
n ⋅π
⋅ EI
P =
n = 0, 1, 2, ...
2
L
Den kleinsten Wert von P ≠ 0 erhält man für n = 1. Daraus folgt die kritische
Knicklast:
2
⋅ EI
P k
= π
2
L
Die zugehörige Knickform ergibt sich dann mit
π ⋅ x
y = C1
⋅sin(
)
L
wobei C 1 die max. Durchbiegung y(x=L/2) in der ausgelenkten Gleichgewichtslage
darstellt. Diese lässt sich nicht explizit angeben, ist aber meist so groß, dass
es zu plastischen Verformungen bzw. zum Versagen des Bauteils kommt.
Weitere Lösungen für n > 1 spielen in der Praxis keine Rolle, da die
zugehörigen Kräfte ein Vielfaches der kritischen Knicklast betragen.
20. Kombinierte Beanspruchung
7

Umwelt-Campus Birkenfeld
Technische Mechanik III
21.2.1 Eulersche Knickfälle
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Die kritische Last ist unabhängig von der Materialfestigkeit, sie hängt nur von
der Biegesteifigkeit und den Lagerungsbedingungen ab.
Führt man eine effektive Knicklänge L k ein, lässt sich die Knicklast für weitere,
erstmals von Euler (1707-1783) untersuchte Knickfälle angeben:
P
k
2
⋅ EI
= π P
L
2
k
Bei gegebener Last P lässt
sich die maximale Knicklänge
berechnen:
L k
= π ⋅
EI
P
Fall 1)
2)
P
3)
P
4)
P
L
Für die Knicksicherheit ist
S k = 3 ... 6 einzuhalten.
L k = L
L k = 2·L
L k = 0,5·L
L k = 0,7·L
20. Kombinierte Beanspruchung
8

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Beispiel 1: Rundstab
Gegeben: L = 8 m, d = 50 mm, E = 200000 N/mm 2
Gesucht: Knicklasten für die Knickfälle 1 - 4
Übung: Stab mit quadratischem Querschnitt
Gegeben: P = 1 kN, a = 24 mm, E = 200000 N/mm 2
Gesucht: Knicklängen für die Knickfälle 1 - 4
20. Kombinierte Beanspruchung
9

Umwelt-Campus Birkenfeld
Technische Mechanik III
Beispiel 2: Gelenkig abgestütztes Aluminium-Profil
Gegeben: I x = 61,2·10 6 mm 4 , I y = 23,2·10 6 mm 4 , P = 50 kN, E = 70000 N/mm 2
Gesucht: Max. Knicklänge und zul. Trägerlänge für eine Knicksicherheit S k = 2
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
P
L
x
z
y
20. Kombinierte Beanspruchung
10

Umwelt-Campus Birkenfeld
Technische Mechanik III
21.2.2 Knickspannung
Mit dem Schlankheitsgrad λ = L k /r ergibt sich schließlich
σ
π
λ
2
k
= E⋅(
/ )
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Die beim Knicken auftretende Spannung ergibt sich aus der Knicklast P k und der
Querschnittsfläche A des Profils
2
Pk
π ⋅ EI
σ
k
= =
2
A L ⋅ A
Mit dem Trägheitsradius
r =
I/A
2
k
k
lässt sich die kritische Knickspannung schreiben in der Form
2
π ⋅ E ⋅r
σ
k
=
L
2
2
π ⋅ E
=
( L / r)
k
2
Die kritische Knickspannung ist diejenige Spannung, bei der ein druckbeanspruchter
Stab durch Ausknicken versagt.
20. Kombinierte Beanspruchung
11

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Trägt man die Knickspannung über dem Schlankheitsgrad auf, ergibt sich eine
Hyperbel, die oberhalb der Proportionalitätsgrenze R p in die sog. Tetmajer-
Gerade übergeht und durch die Streckgrenze R e des Werkstoffs begrenzt wird.
Bei schlanken Stäben oberhalb des
Grenzschlankheitsgrades λ p tritt elastisches
Knicken auf.
Mittelschlanke Stäbe mit λ e < λ< λ p
aus zähem Werkstoff können durch
plastisches Knicken versagen.
Gedrungenen Stäbe versagen durch
Bruch oder Fließen.
Grenzschlankheitsgrade:
Stahl: λ p ≈ 90; λ e ≈ 25
Alu: λ p ≈ 60; λ e ≈ 15
σ k
λ p
2
R e
R p
Bruch
oder
Fließversagen
λ e
plast.
Knicken
Tetmajer-Gerade
Euler-Hyperbel:
⎛π
⎞
σ
k
= E⋅⎜
⎟
⎝ λ ⎠
elast. Knicken
λ
20. Kombinierte Beanspruchung
12

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Beispiel: Dimensionierung eines Stahlstabes
Gegeben: L = 2 m, P = 25 kN, E = 210000 N/mm 2
Gesucht: Durchmesser bei einer Knicksicherheit von S k = 3
A
y
P
S
x
L
α
B
20. Kombinierte Beanspruchung
13

Umwelt-Campus Birkenfeld
Technische Mechanik III
21.3 Real belastete Druckstäbe
mit der allgemeinen Lösung
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Bisher wurden ideal gerade Stäbe und zentrisch angreifende Kräfte angenommenen,
was in der Realität nicht zutrifft. Durch Maßungenauigkeiten kommt es
immer zu einer Exzentrizität e, die gleich zu Beginn der Belastung zu einem
zusätzlichen Biegemoment führt.
M b
= P⋅(
e + y)
P
P
Aus der Beziehung M = −EI·y´´ ergibt sich
die Differentialgleichung
P⋅( e + y)
= −EI
⋅ y''
und mit ω 2 = P/EI folgt
2 2
y''
+ ω ⋅ y + ω ⋅e
= 0
y = C1 ⋅sin( ω ⋅ x)
+ C2
⋅cos(
ω ⋅ x)
−e
L k
e
x
y
y
20. Kombinierte Beanspruchung
14

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Aus den Randbedingungen ergibt sich:
y( x = 0) = 0
y( x = Lk
) = 0 ⇒ C1
= C1 ⋅sin( ω ⋅0)
+ C2
⋅cos(
ω ⋅0)
−e
1−cos(
ω ⋅ Lk
)
= e⋅
sin( ω ⋅ L )
Mit den trigonometrischen Umformungen 1−cos(ω·L) = 2·sin 2 (ω·L/2) und
sin(ω·L) = 2·sin(ω·L/2)·cos(ω·L/2) folgt
C
1
2
2⋅sin
( ω ⋅ Lk
/ 2)
= e⋅
2⋅sin(
ω ⋅ L / 2) ⋅cos(
ω ⋅ L
k
20. Kombinierte Beanspruchung
k
k
sin( ω ⋅ Lk
= e⋅
/ 2) cos( ω ⋅ L
Einsetzen der Konstanten liefert die Biegelinie
⎡ sin( ω ⋅ L
⎤
k
/ 2)
y = e⋅⎢
⋅sin(
ω ⋅ x)
+ cos( ω ⋅ x)
−1⎥
⎣cos(
ω ⋅ Lk
/ 2)
⎦
k
C = e ⇒ 2
/ 2)
/ 2)
Die Durchbiegung y wird sehr groß, wenn der Nenner gegen Null strebt:
ω
cos k
⋅ Lk
= 0
2
15

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Die Gleichung wird erfüllt, wenn
ω k
⋅ L k
π
= n⋅
⇒ω
k
⋅ L k
= n⋅π
2 2
Für die erste Eigenform n = 1 folgt mit ω 2
2
⋅ EI
Pk
= π
k = P k /EI die kritische Knicklast
L
2
k
die mit den Euler-Formeln übereinstimmt.
Die maximale Durchbiegung des Stabes tritt aufgrund der symmetrischen
Belastung bei x = L k /2 auf. Einsetzen liefert
y
max
2
2
⎡sin
( ω ⋅ L
⎤ ⎡ 1 ⎤
k
/ 2) + cos ( ω ⋅ Lk
/ 2)
= e⋅⎢
−1⎥= e⋅⎢
−1⎥
⎣ cos( ω ⋅ L / 2) ⎦ ⎣cos(
ω ⋅ L k
/ 2)
k
⎦
Bei einer Annäherung der Exzentrizität e gegen Null geht auch die Durchbiegung
y max gegen Null. Bei Annäherung an die kritische Knicklast strebt aber
gleichzeitig der Klammerausdruck gegen unendlich, der Ausdruck wird unbestimmt,
der Grenzwert ist von Null verschieden.
20. Kombinierte Beanspruchung
16

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Wird die mit dem Trägheitsradius r = I/A normierte max. Durchbiegung y/r
über dem Verhältnis der Last zur kritischen Knicklast P/P k aufgetragen, nähert
sich die Verformung mit kleiner werdender bezogener Exzentrizität e/r asymptotisch
dem Verhalten des unrealistischen idealen Stabes an.
Mit steigender Exzentrizität
ergeben sich große Verformformungen
schon bei Lasten,
die deutlich unterhalb der
Knicklast liegen
Kommt es durch die Belastung
zum plast. Fließen, erreicht
die Verformungskurve
nicht mehr die Knicklast,
nach Überschreiten des
Maximalwertes verringert
sich die Lastkapazität.
20. Kombinierte Beanspruchung
P/P k Idealer Stab (e = 0)
0,02 0,1 0,2 0,4 0,7 1,0 1,5 e/r = 2
elastisch
plastisch
y max /r
17

Umwelt-Campus Birkenfeld
Technische Mechanik III
Beispiel: Exzentrisch belasteter Rechteckträger
Gegeben: a = 20 mm, b = 12 mm, e = 7 mm, L = 2 m, E = 200000 N/mm 2
Gesucht: Durchbiegung y max bei P = P k /2
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
P
L
z
y
a
x
b
20. Kombinierte Beanspruchung
18

Umwelt-Campus Birkenfeld
Technische Mechanik III
21.3.1 Druckspannungen
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Die Maximalspannung in einem exzentrisch belasteten Druckstab ergibt sich aus
der Überlagerung der axialen Last P und des Biegemoments M
P M σ = +
A W
wobei A die Querschnittsfläche und W das axialen Widerstandsmoment des
Profils darstellen. Mit M = P·(e + y max ) und y max = e ·(1/cos(ω·L k /2) -1) folgt
σ =
P
A
P⋅e
+
W ⋅cos(
ω ⋅ L
k
/ 2)
Beispiel: Exzentrisch belasteter Träger aus vorherigem Beispiel
Gegeben: P = 1450 N, a = 20 mm, b = 12 mm, e = 7 mm, L k = 1,4 m, ω = 0,0909 °/mm
Gesucht: Max. Druckspannung
A = a ⋅b
= 20⋅12
=
σ =
P
A
2
240mm
P ⋅e
+
W ⋅cos(ω⋅
L
k
/2)
=
2
2
W = a ⋅b
/ 6 = 20⋅12
/ 6 =
1450
240
480 mm
1450 ⋅7
+
480 ⋅cos(0,0909
⋅700)
3
= 53,6
N/mm
2
20. Kombinierte Beanspruchung
19

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
21.3.2 Sekantenformel
Setzt man mit dem maßgebenden Randabstand c des Profils W = I/c und berücksichtigt
den Trägheitsradius r = I/A, erhält man mit dem Schlankheitsgrad
λ = L k /r und ω 2 = P/EI die Sekantenformel
σ =
P ⎡
⋅⎢1
+
A ⎣ r
2
⋅cos(
e⋅c
⎤
⎥ ≤σ
P/
EA⋅λ
/ 2) ⎦
Da es sich dabei um eine transzendente
Gleichung handelt, die nicht explizit
nach der Last P aufgelöst werden kann,
lässt sich diese bei gegebener zul.
Spannung nur durch eine numerisches
Verfahren bestimmen.
zul
σ = P/A
σ zul = 250 MPa
e·c/r 2 = 0
0,05
0,1
E = 200000 MPa
Die Abbildung zeigt die Auswertung der Druckspannung P/A in Abhängigkeit
vom Schlankheitsgrad λ=L k /r für verschiedene bezogene Exzentrizitäten ec/r 2 .
0,2
0,3
0,5
1
2
5
σ k =E·( π/λ) 2
λ
20. Kombinierte Beanspruchung
20

Umwelt-Campus Birkenfeld
Technische Mechanik III
der Fachhochschule Trier
Prof. Dr.-Ing. T. Preußler
Beispiel: Exzentrisch belasteter Rechteckträger
Gegeben: a = 24 mm, b = 72 mm, e = 24 mm, L = 2,6 m, E = 200000 N/mm 2 , σ = 250 N/mm 2
Gesucht: Zul. Last P zul und max. Durchbiegung y max
P
L
z
a
x
b
y
Übung: Krit. Last für Knicken um y-Achse
20. Kombinierte Beanspruchung
21