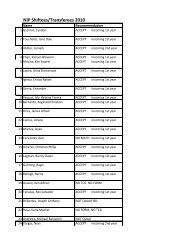
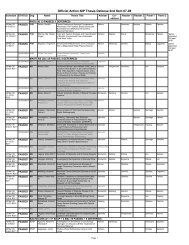
NIP REPORT January 2006- May 2007 - The UP College of Science ...

Importance of the project
The project is timely because it addresses a wide ranging topic that needs resolution, and whose
resolutions have immediate theoretical and practical consequences. Moreover, the availability of
technology needed in confirming our theory makes it even more timely. Its relevance ranges
from foundational issues like quantum measurement theory and interpretations of quantum
mechanics to technologically material issues like data analysis for ultracold atom time of fight
experiments and temporal aspects of quantum tunneling.
Relevance in quantum measurement theory: The eigenfunctions of the confined time of arrival
operators evolve such that the probability of finding the quantum particle at the arrival point is
maximum at their corresponding eigenvalues. In the limit of infinite confining length, the
eigenfunctions evolve to a Dirac delta at the arrival point at their eigenvalues. This dynamical
behavior offers a quantum mechanical picture of the arrival of a quantum particle. And this has a
direct bearing in the long standing quantum measurement problem. In standard quantum
mechanics, there are two known dynamics of a quantum system: The continuous unitary
evolution of the system under Schroedinger's equation, and the discontinuous non-unitary
evolution during quantum measurements. The discontinuity during quantum measurements is
known as wavefunction collapse and it has two distinct aspects: discontinuity in time or quantum
jump, and discontinuity in space or the appearance of particle. The quantum jump occurs when
measurement at some instant of time projects the initial state to another state. The particle
appears when the initial state spontaneously collapses to a state of point support during position
measurement, such as the scintillation on a screen. However, standard quantum mechanics has so
far failed to provide a consistent mechanism on the emergence of these discontinuities from its
own premises, leaving wavefunction collapse an ad hoc hypothesis. This is the well-known
quantum measurement problem (QMP). The QMP has been the source of endless debate on the
proper accounting of quantum mechanics. Existing different approaches to and interpretation of
quantum mechanics have been developed to address these discontinuities. Our quantum theory of
spacetime arrival, however, provides a framework in which the appearance of particles is not a
distinct discontinuity but in fact a consequence of the combined effect of quantum jump and
unitary Schroedinger evolution, reducing the QMP to half.
Relevance in interpretation of quantum mechanics: Because of our theory's implications on the
appearance of particles, it has heavy impact on the interpretation of quantum mechanics. The
majority of the proposed alternative interpretations and formulations of quantum mechanics have
been conjured to address, in particular, the appearance of the particle, for example, Bohmian
mechanics, non-linear quantum mechanics and spontaneous localization theory. In these
alternative formulations, the basic Schroedinger equation is supplemented with additional
features outside standard quantum mechanics to allow for the emergence of particles. The advent
of our theory raises issues against these formulations. Of importance is our theory giving
predictions that is distinct from the predictions of these alternative formulations of quantum
mechanics. Our theory then can play a decisive role in discriminating alternative formulations of
quantum mechanics from the standard formulation. However, our theory may potentially
disagree with the theory of decoherence in the description of particles. Decoherence theory
81