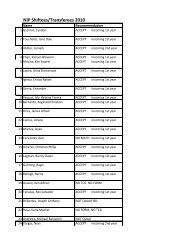
NIP REPORT January 2006- May 2007 - The UP College of Science ...

describes the appearance of particle as the destruction of quantum coherence that eliminates
quantum correlations between spatially separated pieces of the wavepacket. While decoherence
theory is yet to address the quantum arrival problem, it can already be read off from its foregoing
description that the collapse of the wavefunction occurs at the appearance of particle, in contrast
to our description that the collapse occurs right after the preparation of the initial state. However,
any disagreement between decoherence's description and our description needs resolution
because both are within standard quantum mechanics.
Relevance in interpretation of low temperature time of flight measurements: Much of the recent
advances in our understanding of low temperature physics, e.g. Bose-Einstein condensates and
ultracold atoms, has been made possible through time-of-flight measurements [Mo]. In
experiments involving trapped clouds of atoms or condensates, the measurement of the
temperature of the cloud is crucial for characterizing the properties of the traps. The temperature
can be inferred from the velocity distribution of the atoms, which in turn can be measured using
time-of-flight techniques. However, the interpretation of the results of the various time-of-flight
experiments have depended on the calculation of times based on classical trajectories. This
makes the interpretations of the results disputable in the domain of small atomic masses and low
temperatures (or low energy) where quantum mechanical effects are expected to have nonnegligible
aftereffects on the translational motions of the atoms involved. It is known that
existing theory of quantum time of arrival differ with the classical treatment in those regions. It
is this scenario that a full-fledge theory of quantum spacetime arrival is needed in the proper
interpretation of time-of-flights measurements. A correct theory of quantum arrival is then
necessary in the advancement of our knowledge in the low temperature domain.
Relevance in temporal aspects of quantum tunneling: Recently the orthodox interpretation of
quantum tunneling experiments has been critically evaluated and more controversy on the
already controversial quantum time tunneling problem is on the offing. At the heart of the latest
quantum tunneling conundrum is the proper interpretation of the Hartman effect, which,
according to current consensus, implies superluminal or greater-than-the-speed-of-light group
velocities. But it is now claimed that no one has in fact measured superluminal group velocities
in barrier tunneling, and that the purported experimental verifications of superluminal velocities
are misinterpretations of the data. The contention is on the exact physical nature of the group
delay or phase time. The majority opinion is that the phase time is a transit time, so that
superluminal tunneling follows naturally from Hartman effect. But recent thorough analyses
have put this interpretation into question. This then calls for a different theoretical approach to
quantum tunneling, an approach excluding explicit use of the phase time, to independently
confirm the existence or non-existence of superluminal tunneling. This is where quantum arrival
theories can come into play by considering quantum arrival in the transmitted channel. Since our
theory holds for arbitrary interaction potential and arbitrary arrival point, and relevant quantities
are computed via the spectral resolution of the time operator and the initial state alone, our
theory allows us to investigate the existence or non-existence of superluminal barrier tunneling
without the use of phase times.
Feasibility of an experiment: Trapping of ultracold atoms in lattice potentials (potentials
produced by counter propagating lasers) is already common. This makes it possible to design a
time of arrival experiments involving ultracold atoms under lattice potentials. Lattice potentials
82