Fourier Series and Partial Differential Equations Lecture Notes

Chapter 2. Fourier series 18
Theorem 2.2 (Convergence theorem) Let f be a periodic function with period 2π, with
f and f ′ piecewise continuous on (−π,π). Then the Fourier series of f at x converges to
the value 1
2 [f(x+)+f(x−)], i.e.
1
2 [f(x+)+f(x−))] = 1
2 a0 +
∞
[ancos(nx)+bnsin(nx)]. (2.53)
Note that if f is continuous at x, then f(x+) = f(x−) = f(x) so the Fourier series
converges to f(x).
n=0
Note that if a function is defined on an interval of length 2π, we can find the Fourier
series of its periodic extension and equation (2.53) will then hold on the original interval.
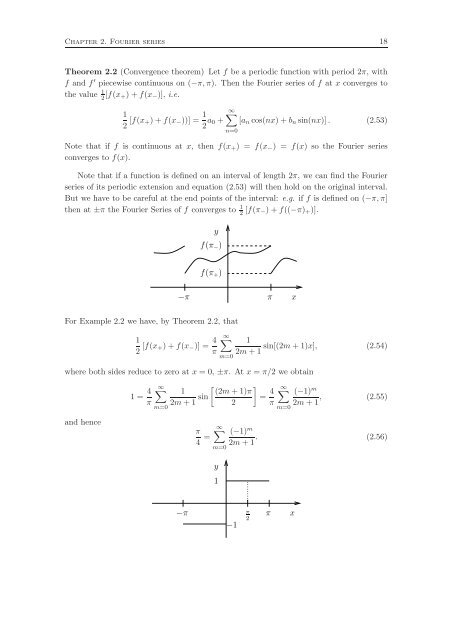
But we have to be careful at the end points of the interval: e.g. if f is defined on (−π,π]
then at ±π the Fourier Series of f converges to 1
2 [f(π−)+f((−π)+)].
−π
y
f(π−)
f(π+)
For Example 2.2 we have, by Theorem 2.2, that
1
2 [f(x+)+f(x−)] = 4
π
∞
m=0
π
x
1
sin[(2m+1)x], (2.54)
2m+1
where both sides reduce to zero at x = 0, ±π. At x = π/2 we obtain
and hence
1 = 4
π
∞ 1
2m+1 sin
(2m+1)π
2
m=0
−π
π
4 =
∞
m=0
y
1
= 4
π
∞
m=0
(−1) m
, (2.55)
2m+1
(−1) m
. (2.56)
2m+1
−1
π
2
π
x