The Discontinuous Conduction Mode Sepic and ´ Cuk Power

636 IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 44, NO. 5, OCTOBER 1997
(a) (b)
(c) (d)
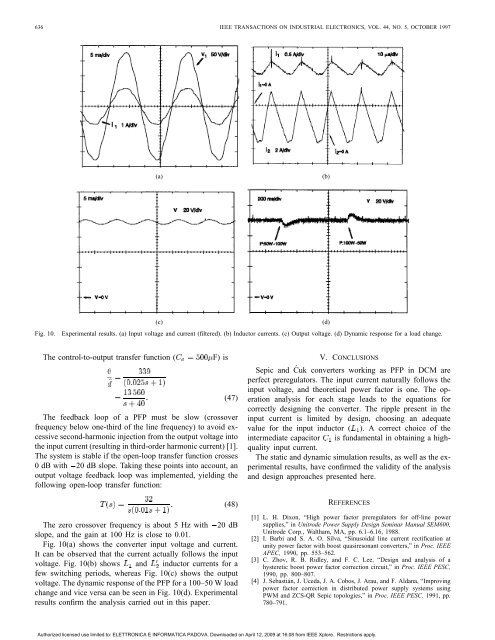
Fig. 10. Experimental results. (a) Input voltage and current (filtered). (b) Inductor currents. (c) Output voltage. (d) Dynamic response for a load change.
The control-to-output transfer function ( F) is
(47)
The feedback loop of a PFP must be slow (crossover
frequency below one-third of the line frequency) to avoid excessive
second-harmonic injection from the output voltage into
the input current (resulting in third-order harmonic current) [1].
The system is stable if the open-loop transfer function crosses
0 dB with 20 dB slope. Taking these points into account, an
output voltage feedback loop was implemented, yielding the
following open-loop transfer function:
(48)
The zero crossover frequency is about 5 Hz with 20 dB
slope, and the gain at 100 Hz is close to 0.01.
Fig. 10(a) shows the converter input voltage and current.
It can be observed that the current actually follows the input
voltage. Fig. 10(b) shows and inductor currents for a
few switching periods, whereas Fig. 10(c) shows the output
voltage. The dynamic response of the PFP for a 100–50 W load
change and vice versa can be seen in Fig. 10(d). Experimental
results confirm the analysis carried out in this paper.
V. CONCLUSIONS
Sepic and Ćuk converters working as PFP in DCM are
perfect preregulators. The input current naturally follows the
input voltage, and theoretical power factor is one. The operation
analysis for each stage leads to the equations for
correctly designing the converter. The ripple present in the
input current is limited by design, choosing an adequate
value for the input inductor ( ). A correct choice of the
intermediate capacitor is fundamental in obtaining a highquality
input current.
The static and dynamic simulation results, as well as the experimental
results, have confirmed the validity of the analysis
and design approaches presented here.
REFERENCES
[1] L. H. Dixon, “High power factor preregulators for off-line power
supplies,” in Unitrode Power Supply Design Seminar Manual SEM600,
Unitrode Corp., Waltham, MA, pp. 6.1–6.16, 1988.
[2] I. Barbi and S. A. O. Silva, “Sinusoidal line current rectification at
unity power factor with boost quasiresonant converters,” in Proc. IEEE
APEC, 1990, pp. 553–562.
[3] C. Zhov, R. B. Ridley, and F. C. Lee, “Design and analysis of a
hysteretic boost power factor correction circuit,” in Proc. IEEE PESC,
1990, pp. 800–807.
[4] J. Sebastián, J. Uceda, J. A. Cobos, J. Arau, and F. Aldana, “Improving
power factor correction in distributed power supply systems using
PWM and ZCS-QR Sepic topologies,” in Proc. IEEE PESC, 1991, pp.
780–791.
Authorized licensed use limited to: ELETTRONICA E INFORMATICA PADOVA. Downloaded on April 12, 2009 at 16:08 from IEEE Xplore. Restrictions apply.