Shared Gaussian Process Latent Variables Models - Oxford Brookes ...

2.7. GAUSSIAN PROCESSES 43
1.5
1
0.5
−3 −2 −1 −0.5 1 2 3
−1
−1.5
−2
−2.5
−3
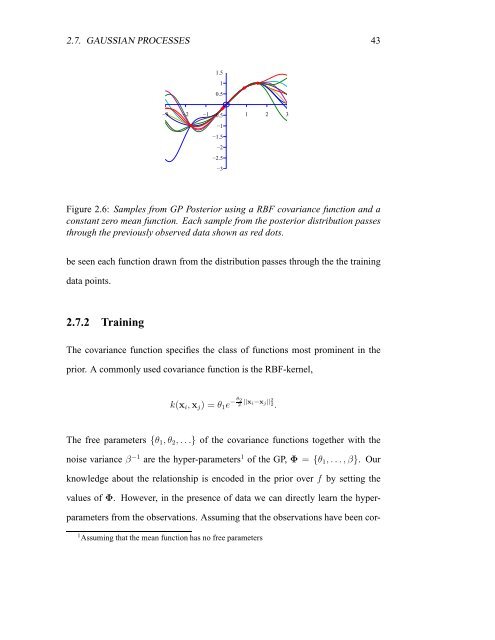
Figure 2.6: Samples from GP Posterior using a RBF covariance function and a
constant zero mean function. Each sample from the posterior distribution passes
through the previously observed data shown as red dots.
be seen each function drawn from the distribution passes through the the training
data points.
2.7.2 Training
The covariance function specifies the class of functions most prominent in the
prior. A commonly used covariance function is the RBF-kernel,
k(xi,xj) = θ1e − θ 2 2 ||xi−xj|| 2 2.
The free parameters {θ1, θ2, . . .} of the covariance functions together with the
noise variance β −1 are the hyper-parameters 1 of the GP, Φ = {θ1, . . .,β}. Our
knowledge about the relationship is encoded in the prior over f by setting the
values of Φ. However, in the presence of data we can directly learn the hyper-
parameters from the observations. Assuming that the observations have been cor-
1 Assuming that the mean function has no free parameters