11DIFFERENTIATION - Department of Mathematics

772 11 DIFFERENTIATION
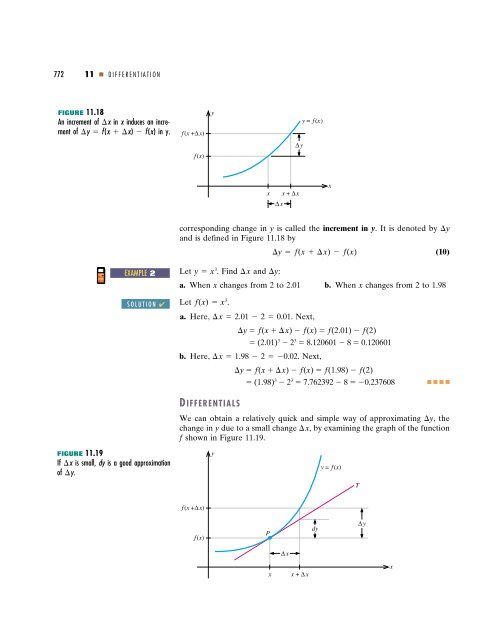
FIGURE 11.18
An increment of x in x induces an increment
of y f(x x) f(x) iny.
EXAMPLE 2
SOLUTION ✔
FIGURE 11.19
If x is small, dy is a good approximation
of y.
f(x +∆x)
f(x)
y
x x + ∆x
∆ x
∆ y
y = f(x)
corresponding change in y is called the increment in y. It is denoted by y
and is defined in Figure 11.18 by
y f(x x) f(x) (10)
Let y x3 . Find x and y:
a. When x changes from 2 to 2.01 b. When x changes from 2 to 1.98
Let f(x) x3 .
a. Here, x 2.01 2 0.01. Next,
y f(x x) f(x) f(2.01) f(2)
(2.01) 3 23 8.120601 8 0.120601
b. Here, x 1.98 2 0.02. Next,
y f(x x) f(x) f(1.98) f(2)
(1.98) 3 23 7.762392 8 0.237608
D IFFERENTIALS
We can obtain a relatively quick and simple way of approximating y, the
change in y due to a small change x, by examining the graph of the function
f shown in Figure 11.19.
f (x +∆x)
f(x)
y
P
∆ x
x x + ∆x
dy
x
y = f (x)
T
∆ y
x