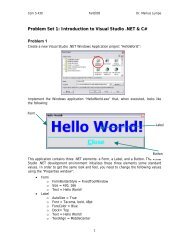
thesis - Faculty of Information and Communication Technologies ...

Chapter 5. Growth Dynamics
mean, median, or standard deviation. Unfortunately, these descriptive
statistics provide little useful information about the distribution
of the data, particularly if it is skewed, as is common with many software
metrics [21,55,118,223,270,299]. Furthermore, the typical longtailed
metric distributions makes precise interpretation with standard
descriptive statistical measures difficult.
Commonly used summary measures such as “arithmetic mean” and
“variance” capture the central tendency in a given data set. However,
where the distribution is strongly skewed, they become much less reliable
in helping understand the shape and changes in the underlying
distribution. Moreover, additional problems may arise due to changes
in both the degree of concentration of individual values and the population
size. Specifically, since these summary measures are influenced
by the population size which tends to increase in evolving software systems.
Descriptive statistics such as median and variance are also likely to be
misleading, given the nature of the underlying distribution. Specifically,
we found that the median measure does not change substantially over
time reducing its effectiveness when applied to understanding software
evolution. An example of this is illustrated in Figure 5.2, where the
median of three different metrics is shown for PMD. As can be seen
in the figure, the median value is very stable over a period of nearly
5 years of evolution. Though there is some change (to the median), in
absolute terms the value does not convey sufficient information about
the nature and dynamics of the evolution.
Additional statistics such as the skew, which measures the asymmetry
of the data, and kurtosis, which measures the peakedness of the
data, may be applied, but are ineffective for comparison between systems
with different population sizes as these measures are unbounded
and change depending on the size of the underlying population, making
relative comparisons ineffective [221]. Given this situation, it is not
surprising that metrics use in industry is not widespread [137]. This
situation is also not helped by the current generation of software metric
tools as many commercial and open source tools [47, 51, 196, 203,
94