A Toy Model of Chemical Reaction Networks - TBI - Universität Wien

46 CHAPTER 5. REACTION NETWORKS
Bipartite graph −→ Substrate graph
O 3
NO 3
NO 2
O 2
−→
O 3
NO 3
NO 2
O 2
−→
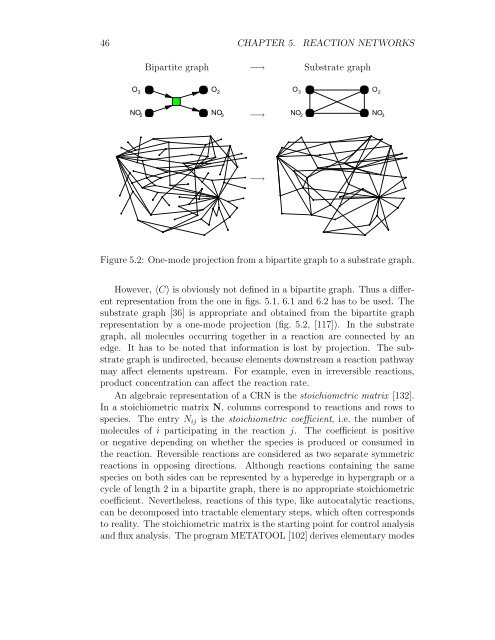
Figure 5.2: One-mode projection from a bipartite graph to a substrate graph.
However, 〈C〉 is obviously not defined in a bipartite graph. Thus a different
representation from the one in figs. 5.1, 6.1 and 6.2 has to be used. The
substrate graph [36] is appropriate and obtained from the bipartite graph
representation by a one-mode projection (fig. 5.2, [117]). In the substrate
graph, all molecules occurring together in a reaction are connected by an
edge. It has to be noted that information is lost by projection. The substrate
graph is undirected, because elements downstream a reaction pathway
may affect elements upstream. For example, even in irreversible reactions,
product concentration can affect the reaction rate.
An algebraic representation of a CRN is the stoichiometric matrix [132].
In a stoichiometric matrix N, columns correspond to reactions and rows to
species. The entry N ij is the stoichiometric coefficient, i.e. the number of
molecules of i participating in the reaction j. The coefficient is positive
or negative depending on whether the species is produced or consumed in
the reaction. Reversible reactions are considered as two separate symmetric
reactions in opposing directions. Although reactions containing the same
species on both sides can be represented by a hyperedge in hypergraph or a
cycle of length 2 in a bipartite graph, there is no appropriate stoichiometric
coefficient. Nevertheless, reactions of this type, like autocatalytic reactions,
can be decomposed into tractable elementary steps, which often corresponds
to reality. The stoichiometric matrix is the starting point for control analysis
and flux analysis. The program METATOOL [102] derives elementary modes