Download the PDF
Download the PDF
Download the PDF
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Instruments Insight<br />
Trusit Dave PhD, BSc, MCOptom, FAAO<br />
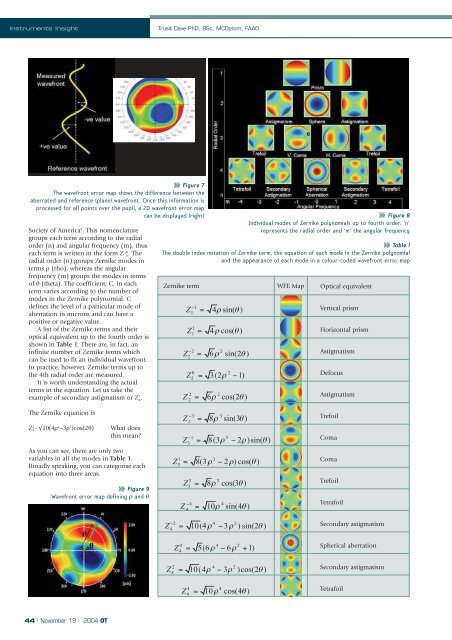
Figure 7<br />
The wavefront error map shows <strong>the</strong> difference between <strong>the</strong><br />
aberrated and reference (plane) wavefront. Once this information is<br />
processed for all points over <strong>the</strong> pupil, a 2D wavefront error map<br />
can be displayed (right) Figure 8<br />
Society of America 4 . This nomenclature<br />
groups each term according to <strong>the</strong> radial<br />
order (n) and angular frequency (m), thus<br />
each term is written in <strong>the</strong> form Z m n. The<br />
radial order (n) groups Zernike modes in<br />
terms ρ (rho), whereas <strong>the</strong> angular<br />
frequency (m) groups <strong>the</strong> modes in terms<br />
of θ (<strong>the</strong>ta). The coefficient, C, in each<br />
term varies according to <strong>the</strong> number of<br />
modes in <strong>the</strong> Zernike polynomial. C<br />
defines <strong>the</strong> level of a particular mode of<br />
aberration in microns and can have a<br />
positive or negative value.<br />
A list of <strong>the</strong> Zernike terms and <strong>the</strong>ir<br />
optical equivalent up to <strong>the</strong> fourth order is<br />
shown in Table 1. There are, in fact, an<br />
infinite number of Zernike terms which<br />
can be used to fit an individual wavefront.<br />
In practice, however, Zernike terms up to<br />
<strong>the</strong> 4th radial order are measured.<br />
It is worth understanding <strong>the</strong> actual<br />
terms in <strong>the</strong> equation. Let us take <strong>the</strong><br />
example of secondary astigmatism or Z 2 4.<br />
−1<br />
Z1 = 4ρ<br />
sin( θ )<br />
1<br />
Z1 = 4ρ<br />
cos( θ )<br />
−<br />
Z<br />
2 6 2<br />
2<br />
= ρ sin(2θ<br />
)<br />
0<br />
2<br />
Z2 = 3(2ρ<br />
−1)<br />
Z<br />
2 = 6ρ<br />
2 cos(2 θ )<br />
2<br />
Individual modes of Zernike polynomials up to fourth order. ‘n’<br />
represents <strong>the</strong> radial order and ‘m’ <strong>the</strong> angular frequency<br />
Table 1<br />
The double index notation of Zernike term, <strong>the</strong> equation of each mode in <strong>the</strong> Zernike polynomial<br />
and <strong>the</strong> appearance of each mode in a colour-coded wavefront error map<br />
Zernike term WFE Map Optical equivalent<br />
Vertical prism<br />
Horizontal prism<br />
Astigmatism<br />
Defocus<br />
Astigmatism<br />
The Zernike equation is<br />
Z 2 4 = √10(4ρ 4 −3ρ 2 )cos(2θ)<br />
What does<br />
this mean?<br />
As you can see, <strong>the</strong>re are only two<br />
variables in all <strong>the</strong> modes in Table 1.<br />
Broadly speaking, you can categorise each<br />
equation into three areas.<br />
Figure 9<br />
Wavefront error map defining ρ and θ<br />
−<br />
Z<br />
3 8 3<br />
3<br />
= ρ sin(3θ<br />
)<br />
−1<br />
3<br />
Z3 = 8(3ρ<br />
− 2ρ)sin(<br />
θ )<br />
1<br />
3<br />
Z3 = 8(3ρ − 2ρ)<br />
cos( θ )<br />
Z<br />
3 = 8ρ<br />
3 cos(3 θ )<br />
3<br />
−<br />
Z<br />
4 10 4<br />
4<br />
= ρ sin(4θ<br />
)<br />
−2<br />
4 2<br />
Z4 = 10(4ρ<br />
−3ρ<br />
) sin(2θ<br />
)<br />
0<br />
4 2<br />
Z4 = 5(6ρ<br />
− 6ρ<br />
+ 1)<br />
2<br />
4 2<br />
Z4 = 10(4ρ<br />
− 3ρ<br />
)cos(2θ<br />
)<br />
Z<br />
4 = 10ρ<br />
4 cos(4 θ )<br />
4<br />
Trefoil<br />
Coma<br />
Coma<br />
Trefoil<br />
Tetrafoil<br />
Secondary astigmatism<br />
Spherical aberration<br />
Secondary astigmatism<br />
Tetrafoil<br />
44 | November 19 | 2004 OT