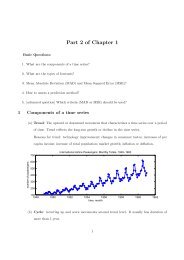
CHAPTER 2: Markov Chains (part 3)

we have
v = 1/(1 − β)
Actually, in this example we can calculate v and u directly.
Example A Maze A white rat is put into the maze
1 2 3
shock
4 5 6
7 8 9
shock
food
In the absence of learning, one might hypothesize that the rat would move through the maze
at random, i.e. if there are k ways to leave a compartment, then the rat would choose each
of them with equal probability 1/k. Assume that the rat makes one changes to some adjacent
compartment at each unit of time. Let X n be the compartment occupied at stage n. Suppose
that compartment 9 contains food and 3 and 7 contain electrical shocking mechanisms.
1. what is the transition probability matrix
P =
1 2 3 4 5 6 7 8 9
1 0 1/2 0 1/2 0 0 0 0 0
2 1/3 0 1/3 0 1/3 0 0 0 0
3 0 0 1 0 0 0 0 0 0
4 1/3 0 0 0 1/3 0 1/3 0 0
5 0 1/4 0 1/4 0 1/4 0 1/4 0
6 0 0 1/3 0 1/3 0 0 0 1/3
7 0 0 0 0 0 0 1 0 0
8 0 0 0 0 1/3 0 1/3 0 1/3
9 0 0 0 0 0 0 0 0 1
2. If the rat starts in compartment 1, what is the probability that the rate encounters food
before being shocked.
Let T = min{n : X n = 3 or X n = 7 or X n = 9}. Let u i = E(X T = 9|X 0 = i), i,e. the
probability that the rat absorbed by food. Note that there are 3 absorbing states 3, 7 and
9. It is easy to see that
u 3 = 0, u 7 = 0, u 9 = 1
2