Intensity-modulated radiotherapy by means of static tomotherapy: A ...

833 M. Oldham and S. Webb: Intensity-modulated radiotherapy 833
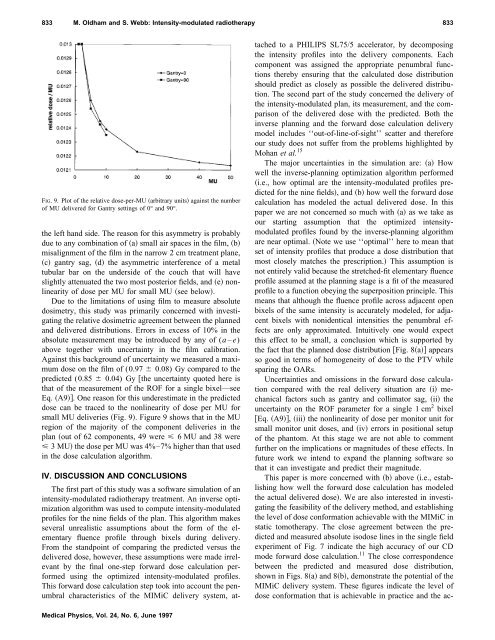
FIG. 9. Plot of the relative dose-per-MU arbitrary units against the number
of MU delivered for Gantry settings of 0° and 90°.
the left hand side. The reason for this asymmetry is probably
due to any combination of a small air spaces in the film, b
misalignment of the film in the narrow 2 cm treatment plane,
c gantry sag, d the asymmetric interference of a metal
tubular bar on the underside of the couch that will have
slightly attenuated the two most posterior fields, and e nonlinearity
of dose per MU for small MU see below.
Due to the limitations of using film to measure absolute
dosimetry, this study was primarily concerned with investigating
the relative dosimetric agreement between the planned
and delivered distributions. Errors in excess of 10% in the
absolute measurement may be introduced by any of (a – e)
above together with uncertainty in the film calibration.
Against this background of uncertainty we measured a maximum
dose on the film of (0.97 0.08) Gy compared to the
predicted (0.85 0.04) Gy the uncertainty quoted here is
that of the measurement of the ROF for a single bixel—see
Eq. A9. One reason for this underestimate in the predicted
dose can be traced to the nonlinearity of dose per MU for
small MU deliveries Fig. 9. Figure 9 shows that in the MU
region of the majority of the component deliveries in the
plan out of 62 components, 49 were 6 MU and 38 were
3MUthe dose per MU was 4%–7% higher than that used
in the dose calculation algorithm.
IV. DISCUSSION AND CONCLUSIONS
The first part of this study was a software simulation of an
intensity-modulated radiotherapy treatment. An inverse optimization
algorithm was used to compute intensity-modulated
profiles for the nine fields of the plan. This algorithm makes
several unrealistic assumptions about the form of the elementary
fluence profile through bixels during delivery.
From the standpoint of comparing the predicted versus the
delivered dose, however, these assumptions were made irrelevant
by the final one-step forward dose calculation performed
using the optimized intensity-modulated profiles.
This forward dose calculation step took into account the penumbral
characteristics of the MIMiC delivery system, attached
to a PHILIPS SL75/5 accelerator, by decomposing
the intensity profiles into the delivery components. Each
component was assigned the appropriate penumbral functions
thereby ensuring that the calculated dose distribution
should predict as closely as possible the delivered distribution.
The second part of the study concerned the delivery of
the intensity-modulated plan, its measurement, and the comparison
of the delivered dose with the predicted. Both the
inverse planning and the forward dose calculation delivery
model includes ‘‘out-of-line-of-sight’’ scatter and therefore
our study does not suffer from the problems highlighted by
Mohan et al. 15
The major uncertainties in the simulation are: a How
well the inverse-planning optimization algorithm performed
i.e., how optimal are the intensity-modulated profiles predicted
for the nine fields, and b how well the forward dose
calculation has modeled the actual delivered dose. In this
paper we are not concerned so much with a as we take as
our starting assumption that the optimized intensitymodulated
profiles found by the inverse-planning algorithm
are near optimal. Note we use ‘‘optimal’’ here to mean that
set of intensity profiles that produce a dose distribution that
most closely matches the prescription. This assumption is
not entirely valid because the stretched-fit elementary fluence
profile assumed at the planning stage is a fit of the measured
profile to a function obeying the superposition principle. This
means that although the fluence profile across adjacent open
bixels of the same intensity is accurately modeled, for adjacent
bixels with nonidentical intensities the penumbral effects
are only approximated. Intuitively one would expect
this effect to be small, a conclusion which is supported by
the fact that the planned dose distribution Fig. 8a appears
so good in terms of homogeneity of dose to the PTV while
sparing the OARs.
Uncertainties and omissions in the forward dose calculation
compared with the real delivery situation are i mechanical
factors such as gantry and collimator sag, ii the
uncertainty on the ROF parameter for a single 1 cm 2 bixel
Eq. A9, iii the nonlinearity of dose per monitor unit for
small monitor unit doses, and iv errors in positional setup
of the phantom. At this stage we are not able to comment
further on the implications or magnitudes of these effects. In
future work we intend to expand the planning software so
that it can investigate and predict their magnitude.
This paper is more concerned with b above i.e., establishing
how well the forward dose calculation has modeled
the actual delivered dose. We are also interested in investigating
the feasibility of the delivery method, and establishing
the level of dose conformation achievable with the MIMiC in
static tomotherapy. The close agreement between the predicted
and measured absolute isodose lines in the single field
experiment of Fig. 7 indicate the high accuracy of our CD
mode forward dose calculation. 11 The close correspondence
between the predicted and measured dose distribution,
shown in Figs. 8a and 8b, demonstrate the potential of the
MIMiC delivery system. These figures indicate the level of
dose conformation that is achievable in practice and the ac-
Medical Physics, Vol. 24, No. 6, June 1997