Quantum Field Theory

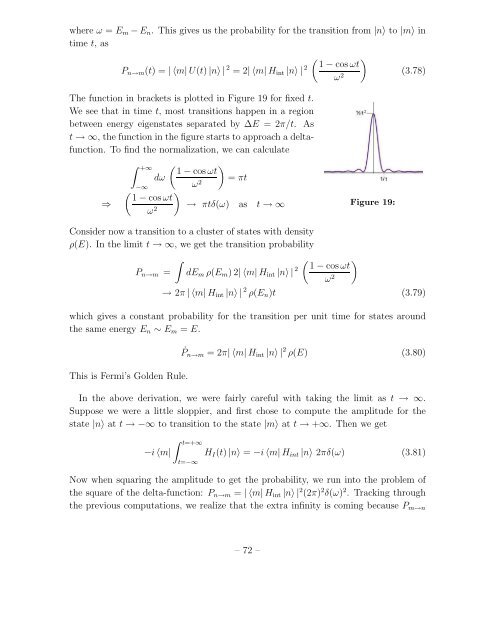
where ω = E m −E n . This gives us the probability for the transition from |n〉 to |m〉 intime t, as( ) 1 − cosωtP n→m (t) = | 〈m| U(t) |n〉 | 2 = 2| 〈m| H int |n〉 | 2 (3.78)ω 2The function in brackets is plotted in Figure 19 for fixed t.We see that in time t, most transitions happen in a regionbetween energy eigenstates separated by ∆E = 2π/t. Ast → ∞, the function in the figure starts to approach a deltafunction.To find the normalization, we can calculate⇒∫ +∞( ) 1 − cos ωtdω = πt−∞ ω( )21 − cosωt→ πtδ(ω) asω 2t → ∞Figure 19:Consider now a transition to a cluster of states with densityρ(E). In the limit t → ∞, we get the transition probability∫( ) 1 − cosωtP n→m = dE m ρ(E m ) 2| 〈m|H int |n〉 | 2 ω 2→ 2π | 〈m| H int |n〉 | 2 ρ(E n )t (3.79)which gives a constant probability for the transition per unit time for states aroundthe same energy E n ∼ E m = E.This is Fermi’s Golden Rule.˙ P n→m = 2π| 〈m|H int |n〉 | 2 ρ(E) (3.80)In the above derivation, we were fairly careful with taking the limit as t → ∞.Suppose we were a little sloppier, and first chose to compute the amplitude for thestate |n〉 at t → −∞ to transition to the state |m〉 at t → +∞. Then we get−i 〈m|∫ t=+∞t=−∞H I (t) |n〉 = −i 〈m|H int |n〉 2πδ(ω) (3.81)Now when squaring the amplitude to get the probability, we run into the problem ofthe square of the delta-function: P n→m = | 〈m| H int |n〉 | 2 (2π) 2 δ(ω) 2 . Tracking throughthe previous computations, we realize that the extra infinity is coming because P m→n– 72 –