Design and Simulation of Active Suspension System by Using Matlab

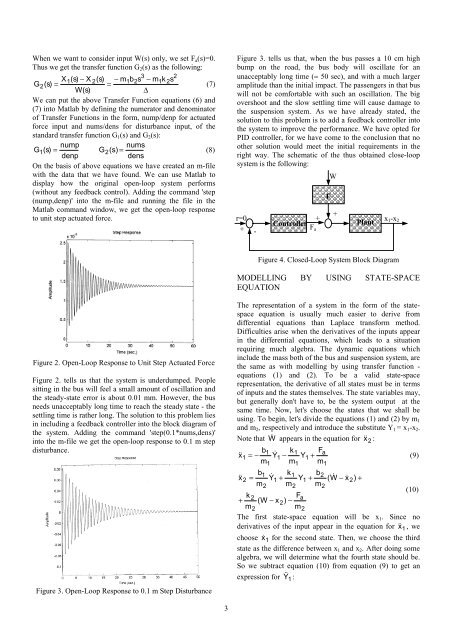
When we want to consider input W(s) only, we set F a (s)=0.Thus we get the transfer function G 2 (s) as the following:3 2X1(s)− X 2(s)− m1b2s− m1k2sG 2(s)==(7)W(s)∆We can put the above Transfer Function equations (6) and(7) into Matlab by defining the numerator and denominatorof Transfer Functions in the form, nump/denp for actuatedforce input and nums/dens for disturbance input, of thestandard transfer function G 1 (s) and G 2 (s):numpnumsG1 (s) = G2(s)=(8)denpdensOn the basis of above equations we have created an m-filewith the data that we have found. We can use Matlab todisplay how the original open-loop system performs(without any feedback control). Adding the command 'step(nump,denp)' into the m-file and running the file in theMatlab command window, we get the open-loop responseto unit step actuated force.Figure 3. tells us that, when the bus passes a 10 cm highbump on the road, the bus body will oscillate for anunacceptably long time (≈ 50 sec), and with a much largeramplitude than the initial impact. The passengers in that buswill not be comfortable with such an oscillation. The bigovershoot and the slow settling time will cause damage tothe suspension system. As we have already stated, thesolution to this problem is to add a feedback controller intothe system to improve the performance. We have opted forPID controller, for we have come to the conclusion that noother solution would meet the initial requirements in theright way. The schematic of the thus obtained close-loopsystem is the following:r=0 ++ControllerPlantx -x 1 2+ F-aFWFigure 4. Closed-Loop System Block DiagramMODELLING BY USING STATE-SPACEEQUATIONFigure 2. Open-Loop Response to Unit Step Actuated ForceFigure 2. tells us that the system is underdumped. Peoplesitting in the bus will feel a small amount of oscillation andthe steady-state error is about 0.01 mm. However, the busneeds unacceptably long time to reach the steady state - thesettling time is rather long. The solution to this problem liesin including a feedback controller into the block diagram ofthe system. Adding the command 'step(0.1*nums,dens)'into the m-file we get the open-loop response to 0.1 m stepdisturbance.Figure 3. Open-Loop Response to 0.1 m Step DisturbanceThe representation of a system in the form of the statespaceequation is usually much easier to derive fromdifferential equations than Laplace transform method.Difficulties arise when the derivatives of the inputs appearin the differential equations, which leads to a situationrequiring much algebra. The dynamic equations whichinclude the mass both of the bus and suspension system, arethe same as with modelling by using transfer function -equations (1) and (2). To be a valid state-spacerepresentation, the derivative of all states must be in termsof inputs and the states themselves. The state variables may,but generally don't have to, be the system output at thesame time. Now, let's choose the states that we shall beusing. To begin, let's divide the equations (1) and (2) by m 1and m 2 , respectively and introduce the substitute Y 1 = x 1 -x 2 .Note that W appears in the equation for x 2 :b1k1F ax 1 = − Y1 − Y1+(9)m1m1m1b1k1b2x2= Y1 + Y1+ (W− x2)+m2m2m2(10)k 2Fa+ (W − x2)−m2m2The first state-space equation will be x 1 . Since noderivatives of the input appear in the equation for x 1 , wechoose x 1 for the second state. Then, we choose the thirdstate as the difference between x 1 and x 2 . After doing somealgebra, we will determine what the fourth state should be.So we subtract equation (10) from equation (9) to get anexpression for Y 1 :3