Upgrade Report - Department of Informatics - King's College London

More documents

Recommendations

Info

5 GRAPH GENERATION MODELS 11Figure 4: Degree distribution of the triangle closing graph with random-random selection policy5.4 Triangle Closing ModelThis model was created based on the observation that most links in OSNs are local, no more than 2 hopsapart [36]. There are several variations of this model discussed but it all follows the idea that a vertex arrivesin the network and creates an edge to another vertex at random. Then it proceeds in forming additionallinks by selecting a vertex which is 2 hops away from it. The way the vertex is selected depends on a givenpolicy and there are several policies mentioned in.However it was suggested by Leskovec that the random neighbor of random neighbor policy is thesimplest one and worked surprisingly well when the generated graphs were compared to some real OSNswith respect to how each vertex directs edges to other vertices. While other policies, such as most activeneighbor of most active neighbor, may work better the increase in accuracy is marginal [36].The resulting degree distribution from the above generation model can be seen in Figure 4.5.5 Forest Fire ModelThis model, first proposed by Leskovec et al [39] is a model which is an intuitive model on how OSNs evolveover time. It is very similar to the triangle closing model when viewed from the perspective of the localityof new links. Additionally it has the advantages on not only generating degree distribution power-laws inboth directions but also in generating communities. Moreover the edge densification power-law [31] holdsfor each step of the generative process and the diameter decreases at each step.The method is as follows:• At each step we add a new vertex v and direct m edges to other vertices u 1 , · · · , u m selected UAR.We call these vertices ambassadors of v• Recursively for each new edge e i = (v, u n ) added we generate two random numbers x and y whichfollow a geometric distribution with meansrespectively. Where 0 ≤ p, r < 1.p1−p and• We obtain two sets of edges S 1 = {s 1 , · · · , s x } S 2 = {s x+1 , · · · , s x+y } where ∃e 1 = (u n , s i )∀s i ∈ S 1or ∃e 2 = (s j , u n )∀s j ∈ S 2rp1−rp
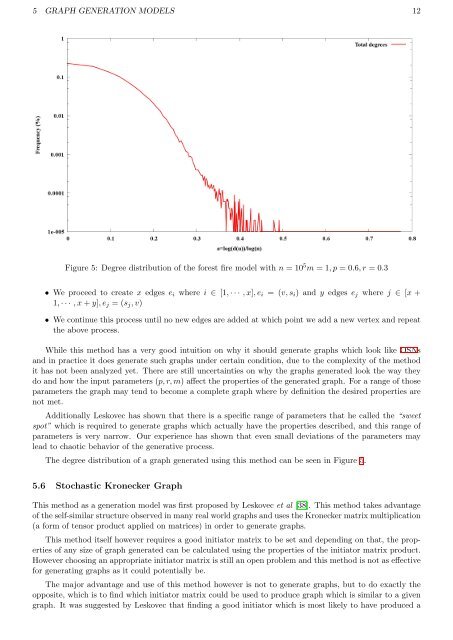
5 GRAPH GENERATION MODELS 12Figure 5: Degree distribution of the forest fire model with n = 10 5 m = 1, p = 0.6, r = 0.3• We proceed to create x edges e i where i ∈ [1, · · · , x], e i = (v, s i ) and y edges e j where j ∈ [x +1, · · · , x + y], e j = (s j , v)• We continue this process until no new edges are added at which point we add a new vertex and repeatthe above process.While this method has a very good intuition on why it should generate graphs which look like OSNsand in practice it does generate such graphs under certain condition, due to the complexity of the methodit has not been analyzed yet. There are still uncertainties on why the graphs generated look the way theydo and how the input parameters (p, r, m) affect the properties of the generated graph. For a range of thoseparameters the graph may tend to become a complete graph where by definition the desired properties arenot met.Additionally Leskovec has shown that there is a specific range of parameters that he called the “sweetspot” which is required to generate graphs which actually have the properties described, and this range ofparameters is very narrow. Our experience has shown that even small deviations of the parameters maylead to chaotic behavior of the generative process.The degree distribution of a graph generated using this method can be seen in Figure 5.5.6 Stochastic Kronecker GraphThis method as a generation model was first proposed by Leskovec et al [38]. This method takes advantageof the self-similar structure observed in many real world graphs and uses the Kronecker matrix multiplication(a form of tensor product applied on matrices) in order to generate graphs.This method itself however requires a good initiator matrix to be set and depending on that, the propertiesof any size of graph generated can be calculated using the properties of the initiator matrix product.However choosing an appropriate initiator matrix is still an open problem and this method is not as effectivefor generating graphs as it could potentially be.The major advantage and use of this method however is not to generate graphs, but to do exactly theopposite, which is to find which initiator matrix could be used to produce graph which is similar to a givengraph. It was suggested by Leskovec that finding a good initiator which is most likely to have produced a
Page 1 and 2: King’s College LondonDepartment o
Page 3 and 4: 7.5 Partitioned Preferential Attach
Page 5 and 6: List of Figures1 Erdós-Rényi Grap
Page 7 and 8: 2Part IIntroduction1 Online Social
Page 9 and 10: 4Part IIRelated Work4 Network prope
Page 11 and 12: 4 NETWORK PROPERTIES AND METRICS 6W
Page 13 and 14: 5 GRAPH GENERATION MODELS 8Figure 1
Page 15: 5 GRAPH GENERATION MODELS 10Figure
Page 19 and 20: 6 GRAPH SAMPLING AND CRAWLING 14on
Page 21 and 22: 6 GRAPH SAMPLING AND CRAWLING 16In
Page 23 and 24: 6 GRAPH SAMPLING AND CRAWLING 18{a(
Page 25 and 26: 7 GRAPH GENERATION 20(a) Constant m
Page 27 and 28: 7 GRAPH GENERATION 22Figure 9: Grow
Page 29 and 30: 7 GRAPH GENERATION 24Figure 10: Imp
Page 31 and 32: 8 EXISTING DATA SET ANALYSIS 26From
Page 33 and 34: 8 EXISTING DATA SET ANALYSIS 28From
Page 35 and 36: 9 GRAPH SAMPLING 30calls. We presen
Page 37 and 38: 9 GRAPH SAMPLING 32Figure 19: Real
Page 39 and 40: 9 GRAPH SAMPLING 34where b > 0 cons
Page 41 and 42: 9 GRAPH SAMPLING 36Theorem 3. For c
Page 43 and 44: 9 GRAPH SAMPLING 38Figure 22: Plots
Page 45 and 46: 9 GRAPH SAMPLING 40wide range of re
Page 47 and 48: 11 GRAPH SAMPLING 42In addition to
Page 49 and 50: 12 GRAPH GENERATION MODELS 4411.1.3
Page 51 and 52: 46Part VReferencesReferences[1] Dim
Page 53 and 54: REFERENCES 48[36] Jure Leskovec, La
Page 55 and 56: 50Part VIAppendixASampling Manufact
Page 57 and 58: A SAMPLING MANUFACTURED GRAPHS: BFS

Upgrade Report - Department of Informatics - King's College London

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?