Upgrade Report - Department of Informatics - King's College London

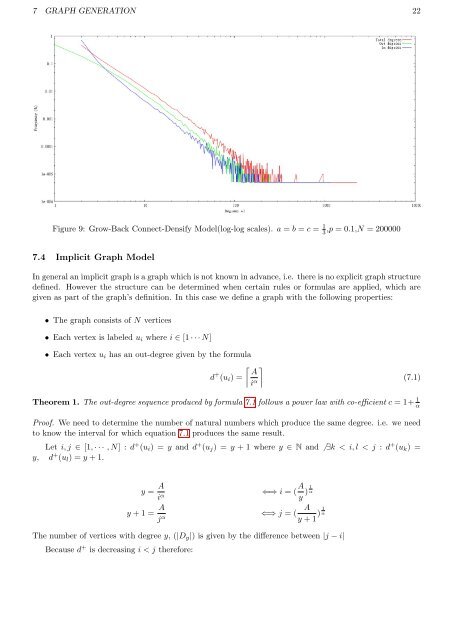
7 GRAPH GENERATION 22Figure 9: Grow-Back Connect-Densify Model(log-log scales). a = b = c = 1 3,p = 0.1,N = 2000007.4 Implicit Graph ModelIn general an implicit graph is a graph which is not known in advance, i.e. there is no explicit graph structuredefined. However the structure can be determined when certain rules or formulas are applied, which aregiven as part of the graph’s definition. In this case we define a graph with the following properties:• The graph consists of N vertices• Each vertex is labeled u i where i ∈ [1 · · · N]• Each vertex u i has an out-degree given by the formula⌈ ⌉ Ad + (u i ) =i α(7.1)Theorem 1. The out-degree sequence produced by formula 7.1 follows a power law with co-efficient c = 1+ 1 αProof. We need to determine the number of natural numbers which produce the same degree. i.e. we needto know the interval for which equation 7.1 produces the same result.Let i, j ∈ [1, · · · , N] : d + (u i ) = y and d + (u j ) = y + 1 where y ∈ N and ̸ ∃k < i, l < j : d + (u k ) =y, d + (u l ) = y + 1.y = A i α⇐⇒ i = ( A y ) 1 αy + 1 = A Aj α ⇐⇒ j = (y + 1 ) 1 αThe number of vertices with degree y, (|D y |) is given by the difference between |j − i|Because d + is decreasing i < j therefore: