- Page 1:
University Physics I: Classical Mec
- Page 5 and 6:
ii
- Page 7 and 8:
iv CONTENTS 1.6 Problems . . . . .
- Page 9 and 10:
vi CONTENTS 5.1 Conservative intera
- Page 11 and 12:
viii CONTENTS 7.7 Examples . . . .
- Page 13 and 14:
x CONTENTS 10.4 Examples . . . . .
- Page 15 and 16:
xii CONTENTS 13.2.1 Temperature and
- Page 17 and 18:
xiv CONTENTS they have read. Then,
- Page 19 and 20:
Chapter 1 Reference frames, displac
- Page 21 and 22:
1.2. POSITION, DISPLACEMENT, VELOCI
- Page 23 and 24:
1.2. POSITION, DISPLACEMENT, VELOCI
- Page 25 and 26:
1.2. POSITION, DISPLACEMENT, VELOCI
- Page 27 and 28:
1.2. POSITION, DISPLACEMENT, VELOCI
- Page 29 and 30:
1.2. POSITION, DISPLACEMENT, VELOCI
- Page 31 and 32:
1.2. POSITION, DISPLACEMENT, VELOCI
- Page 33 and 34:
1.3. REFERENCE FRAME CHANGES AND RE
- Page 35 and 36:
1.3. REFERENCE FRAME CHANGES AND RE
- Page 37 and 38:
1.4. IN SUMMARY 19 with a velocity
- Page 39 and 40:
1.5. EXAMPLES 21 1.5 Examples 1.5.1
- Page 41 and 42:
1.5. EXAMPLES 23 (twice what it was
- Page 43 and 44: 1.5. EXAMPLES 25 Note that I have d
- Page 45 and 46: 1.6. PROBLEMS 27 1.6 Problems Probl
- Page 47 and 48: 1.6. PROBLEMS 29 Problem 5 You are
- Page 49 and 50: Chapter 2 Acceleration 2.1 The law
- Page 51 and 52: 2.1. THE LAW OF INERTIA 33 This is
- Page 53 and 54: 2.2. ACCELERATION 35 2.2 Accelerati
- Page 55 and 56: 2.2. ACCELERATION 37 called “conc
- Page 57 and 58: 2.2. ACCELERATION 39 2.2.2 Motion w
- Page 59 and 60: 2.2. ACCELERATION 41 2.2.3 Accelera
- Page 61 and 62: 2.3. FREE FALL 43 proportional to t
- Page 63 and 64: 2.4. IN SUMMARY 45 4. Changes in ve
- Page 65 and 66: 2.5. EXAMPLES 47 which the rocket r
- Page 67 and 68: 2.6. PROBLEMS 49 (a) How far did yo
- Page 69 and 70: Chapter 3 Momentum and Inertia 3.1
- Page 71 and 72: 3.1. INERTIA 53 reliable, repeatabl
- Page 73 and 74: 3.1. INERTIA 55 3.1.2 Inertial mass
- Page 75 and 76: 3.2. MOMENTUM 57 the system is p i
- Page 77 and 78: 3.3. EXTENDED SYSTEMS AND CENTER OF
- Page 79 and 80: 3.4. IN SUMMARY 61 3.3.2 Recoil and
- Page 81 and 82: 3.5. EXAMPLES 63 3.5 Examples 3.5.1
- Page 83 and 84: 3.5. EXAMPLES 65 3.5.2 Collision in
- Page 85 and 86: 3.6. PROBLEMS 67 3.6 Problems Probl
- Page 87 and 88: Chapter 4 Kinetic Energy 4.1 Kineti
- Page 89 and 90: 4.1. KINETIC ENERGY 71 v 2i =0,v 1f
- Page 91 and 92: 4.1. KINETIC ENERGY 73 special case
- Page 93: 4.1. KINETIC ENERGY 75 This immedia
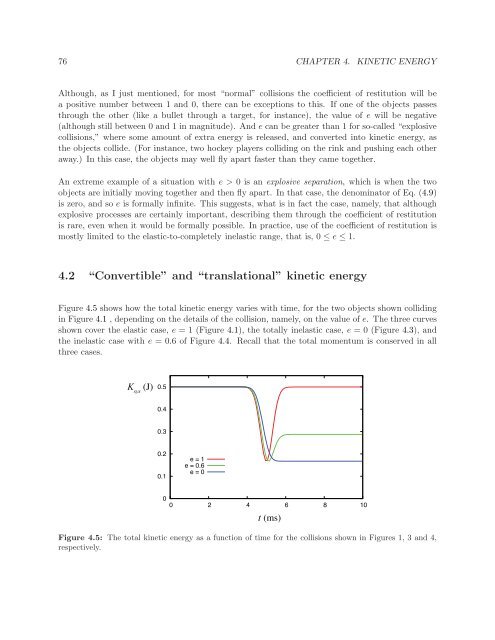
- Page 97 and 98: 4.2. “CONVERTIBLE” AND “TRANS
- Page 99 and 100: 4.3. IN SUMMARY 81 7. Besides the c
- Page 101 and 102: 4.4. EXAMPLES 83 On the other hand,
- Page 103 and 104: 4.4. EXAMPLES 85 K cm ′ = 1 2 (m
- Page 105 and 106: 4.5. PROBLEMS 87 (a) What is the in
- Page 107 and 108: Chapter 5 Interactions and energy 5
- Page 109 and 110: 5.1. CONSERVATIVE INTERACTIONS 91 T
- Page 111 and 112: 5.1. CONSERVATIVE INTERACTIONS 93 A
- Page 113 and 114: 5.1. CONSERVATIVE INTERACTIONS 95 d
- Page 115 and 116: 5.2. DISSIPATION OF ENERGY AND THER
- Page 117 and 118: 5.4. CONSERVATION OF ENERGY 99 leve
- Page 119 and 120: 5.5. IN SUMMARY 101 gravitational p
- Page 121 and 122: 5.6. EXAMPLES 103 5.6 Examples 5.6.
- Page 123 and 124: 5.6. EXAMPLES 105 problem involves
- Page 125 and 126: 5.7. ADVANCED TOPICS 107 where the
- Page 127 and 128: 5.8. PROBLEMS 109 5.8 Problems Prob
- Page 129 and 130: 5.8. PROBLEMS 111 here? Explain. (f
- Page 131 and 132: Chapter 6 Interactions, part 2: For
- Page 133 and 134: 6.1. FORCE 115 however, somewhat mo
- Page 135 and 136: 6.2. FORCES AND POTENTIAL ENERGY 11
- Page 137 and 138: 6.2. FORCES AND POTENTIAL ENERGY 11
- Page 139 and 140: 6.3. FORCES NOT DERIVED FROM A POTE
- Page 141 and 142: 6.3. FORCES NOT DERIVED FROM A POTE
- Page 143 and 144: 6.3. FORCES NOT DERIVED FROM A POTE
- Page 145 and 146:
6.5. IN SUMMARY 127 F s,1 n a F s,1
- Page 147 and 148:
6.6. EXAMPLES 129 6.6 Examples 6.6.
- Page 149 and 150:
6.6. EXAMPLES 131 pushes on the bra
- Page 151 and 152:
6.6. EXAMPLES 133 This is a huge di
- Page 153 and 154:
6.7. PROBLEMS 135 Problem 6 Draw a
- Page 155 and 156:
Chapter 7 Impulse, Work and Power 7
- Page 157 and 158:
7.2. WORK ON A SINGLE PARTICLE 139
- Page 159 and 160:
7.3. THE “CENTER OF MASS WORK”
- Page 161 and 162:
7.4. WORK DONE ON A SYSTEM BY ALL T
- Page 163 and 164:
7.4. WORK DONE ON A SYSTEM BY ALL T
- Page 165 and 166:
7.4. WORK DONE ON A SYSTEM BY ALL T
- Page 167 and 168:
7.4. WORK DONE ON A SYSTEM BY ALL T
- Page 169 and 170:
7.6. IN SUMMARY 151 which is equal
- Page 171 and 172:
7.7. EXAMPLES 153 7.7 Examples 7.7.
- Page 173 and 174:
7.7. EXAMPLES 155 To plot all this
- Page 175 and 176:
7.7. EXAMPLES 157 (a) The external
- Page 177 and 178:
7.8. PROBLEMS 159 Problem 5 A block
- Page 179 and 180:
Chapter 8 Motion in two dimensions
- Page 181 and 182:
8.1. DEALING WITH FORCES IN TWO DIM
- Page 183 and 184:
8.2. PROJECTILE MOTION 165 The over
- Page 185 and 186:
8.3. INCLINED PLANES 167 8.3 Inclin
- Page 187 and 188:
8.4. MOTION ON A CIRCLE (OR PART OF
- Page 189 and 190:
8.4. MOTION ON A CIRCLE (OR PART OF
- Page 191 and 192:
8.4. MOTION ON A CIRCLE (OR PART OF
- Page 193 and 194:
8.5. IN SUMMARY 175 As we shall see
- Page 195 and 196:
8.6. EXAMPLES 177 8.6 Examples You
- Page 197 and 198:
8.7. ADVANCED TOPICS 179 8.7 Advanc
- Page 199 and 200:
8.7. ADVANCED TOPICS 181 Now we jus
- Page 201 and 202:
8.7. ADVANCED TOPICS 183 Note that
- Page 203 and 204:
8.7. ADVANCED TOPICS 185 The cyan a
- Page 205 and 206:
8.8. PROBLEMS 187 (b) What is the w
- Page 207 and 208:
8.8. PROBLEMS 189 (e) The power is
- Page 209 and 210:
Chapter 9 Rotational dynamics Rotat
- Page 211 and 212:
9.2. ANGULAR MOMENTUM 193 9.2 Angul
- Page 213 and 214:
9.2. ANGULAR MOMENTUM 195 thing is
- Page 215 and 216:
9.3. THE CROSS PRODUCT AND ROTATION
- Page 217 and 218:
9.3. THE CROSS PRODUCT AND ROTATION
- Page 219 and 220:
9.4. TORQUE 201 momentum involves t
- Page 221 and 222:
9.4. TORQUE 203 wrenches). It is al
- Page 223 and 224:
9.5. STATICS 205 important in engin
- Page 225 and 226:
9.6. ROLLING MOTION 207 9.6 Rolling
- Page 227 and 228:
9.6. ROLLING MOTION 209 contact wit
- Page 229 and 230:
9.7. IN SUMMARY 211 (Note how I hav
- Page 231 and 232:
9.8. EXAMPLES 213 9.8 Examples This
- Page 233 and 234:
9.8. EXAMPLES 215 Solution The figu
- Page 235 and 236:
9.9. PROBLEMS 217 9.9 Problems Prob
- Page 237 and 238:
9.9. PROBLEMS 219 A 20-kg plank of
- Page 239 and 240:
Chapter 10 Gravity 10.1 The inverse
- Page 241 and 242:
10.1. THE INVERSE-SQUARE LAW 223 ne
- Page 243 and 244:
10.1. THE INVERSE-SQUARE LAW 225 it
- Page 245 and 246:
10.1. THE INVERSE-SQUARE LAW 227 in
- Page 247 and 248:
10.1. THE INVERSE-SQUARE LAW 229 an
- Page 249 and 250:
10.1. THE INVERSE-SQUARE LAW 231 el
- Page 251 and 252:
10.1. THE INVERSE-SQUARE LAW 233 10
- Page 253 and 254:
10.1. THE INVERSE-SQUARE LAW 235 Fr
- Page 255 and 256:
10.2. WEIGHT, ACCELERATION, AND THE
- Page 257 and 258:
10.2. WEIGHT, ACCELERATION, AND THE
- Page 259 and 260:
10.3. IN SUMMARY 241 shifted and/or
- Page 261 and 262:
10.4. EXAMPLES 243 10.4 Examples 10
- Page 263 and 264:
10.4. EXAMPLES 245 The diagram of t
- Page 265 and 266:
10.5. ADVANCED TOPICS 247 10.5 Adva
- Page 267 and 268:
10.6. PROBLEMS 249 10.6 Problems Pr
- Page 269 and 270:
10.6. PROBLEMS 251 an orbit around
- Page 271 and 272:
Chapter 11 Simple harmonic motion 1
- Page 273 and 274:
11.2. SIMPLE HARMONIC MOTION 255 is
- Page 275 and 276:
11.2. SIMPLE HARMONIC MOTION 257 Th
- Page 277 and 278:
11.2. SIMPLE HARMONIC MOTION 259 If
- Page 279 and 280:
11.2. SIMPLE HARMONIC MOTION 261 Th
- Page 281 and 282:
11.3. PENDULUMS 263 o θ l F t F G
- Page 283 and 284:
11.3. PENDULUMS 265 11.3.2 The “p
- Page 285 and 286:
11.4. IN SUMMARY 267 9. A simple pe
- Page 287 and 288:
11.5. EXAMPLES 269 (b) The amplitud
- Page 289 and 290:
11.5. EXAMPLES 271 AsshowninSection
- Page 291 and 292:
11.6. ADVANCED TOPICS 273 Figure 11
- Page 293 and 294:
11.6. ADVANCED TOPICS 275 the oscil
- Page 295 and 296:
11.7. PROBLEMS 277 (that is, with r
- Page 297 and 298:
Chapter 12 Waves in one dimension 1
- Page 299 and 300:
12.1. TRAVELING WAVES 281 Perhaps t
- Page 301 and 302:
12.1. TRAVELING WAVES 283 ξ 1 0.5
- Page 303 and 304:
12.1. TRAVELING WAVES 285 Comparing
- Page 305 and 306:
12.1. TRAVELING WAVES 287 waves, th
- Page 307 and 308:
12.2. STANDING WAVES AND RESONANCE
- Page 309 and 310:
12.2. STANDING WAVES AND RESONANCE
- Page 311 and 312:
12.3. CONCLUSION, AND FURTHER RESOU
- Page 313 and 314:
12.5. EXAMPLES 295 12.5 Examples 12
- Page 315 and 316:
12.5. EXAMPLES 297 However, if you
- Page 317 and 318:
12.6. ADVANCED TOPICS 299 12.6 Adva
- Page 319 and 320:
12.6. ADVANCED TOPICS 301 In the lo
- Page 321 and 322:
Chapter 13 Thermodynamics 13.1 Intr
- Page 323 and 324:
13.2. INTRODUCING TEMPERATURE 305 a
- Page 325 and 326:
13.2. INTRODUCING TEMPERATURE 307 m
- Page 327 and 328:
13.3. HEAT AND THE FIRST LAW 309 th
- Page 329 and 330:
13.3. HEAT AND THE FIRST LAW 311 ca
- Page 331 and 332:
13.4. THE SECOND LAW AND ENTROPY 31
- Page 333 and 334:
13.4. THE SECOND LAW AND ENTROPY 31
- Page 335 and 336:
13.4. THE SECOND LAW AND ENTROPY 31
- Page 337 and 338:
13.5. IN SUMMARY 319 13.5 In summar
- Page 339 and 340:
13.6. EXAMPLES 321 13.6 Examples 13
- Page 341 and 342:
13.7. PROBLEMS 323 13.7 Problems Pr