Apunte sobre perturbaciones singulares

4.1. PERTURBACIONES SINGULARES 1
4.1 Perturbaciones Singulares
Mientras que los métodos perturbacionales, como el de Linstedt-Poincaré, o los de promediación
de Krylov-Boguliubov se aplican a sistemas que dependen suavemente de un parámetro μ, en
esta sección se considera un problema mucho más complicado: la dependencia discontinua de
las propiedades del sistema en función de un parámetro ε. El esquema del problema típico de
perturbaciones singulares es
ẋ = f(t, x, z, ε),
εż = g(t, x, z, ε),
donde hacer ε =0causa un cambio abrupto en las propiedades dinámicas del sistema, pues la
ecuación diferencial εż = g(t, x, z, ε) degenera en la ecuación algebraica o trascendental
0=g(t, x, z, ε).
La esencia de la teoría es que la discontinuidad de las soluciones causada por las perturbaciones
singulares puede evitarse si se analizan en escalas de tiempo diferentes. Esta aproximación con
múltiples escalas de tiempo es un rasgo distintivo del método de las perturbaciones singulares.
4.2 El modelo típico de perturbaciones singulares
El modelo de perturbaciones singulares de un sistema dinámico es un modelo de estado donde las
derivadas de algunos estados están multiplicadas por un pequeño parámetro positivo ε :
ẋ = f(t, x, z, ε), (4.1)
εż = g(t, x, z, ε). (4.2)
Se supondrá que las funciones f y g son continuamente diferenciables en sus argumentos, para
t ∈ [0,t 1 ],x∈ X ⊂ R n ,x∈ Z ⊂ R m , donde X y Z son subconjuntos abiertos de R n y R m ,
respectivamente. Cuando se hace ε =0en (4.1) y (4.2) la dimensión del sistema cambia de m + n
a n porque la ecuación diferencial (4.2) degenera en
0=g(t, x, z, ε). (4.3)
Se dice que el modelo (4.1)-(4.2) está en la forma típica si (4.3) tiene k ≥ 1 raíces reales aisladas,
z = h i (t, x), i =1, 2,...,k, (4.4)
para cada t ∈ [0,t 1 ] ycadax ∈ X. Esta hipótesis asegura que a cada raíz de (4.3) corresponde un
modelo reducido bien definido, los que se obtienen sustituyendo (4.4) en (4.1), con ε =0, resultando
en
ẋ = f[t, x, h(t, x), 0] (4.5)
donde se ha suprimido el subíndice i de h; quedará claro del contexto cuál de las k raíces de (4.3) es
la que se está usando. El modelo reducido (4.5) se suele llamar modelo de estado casi estacionario
porque las variables z (cuya velocidad ż = g/ε puede ser muy elevada cuando ε es pequeño y g 6= 0)
puede converger rápidamente a alguna de las raíces de (4.3), que son puntos de equilibrio de (4.2);
el modelo (4.5) también se conoce como modelo lento. La propiedad de una doble escala de tiempo
rápido/lento de (4.1)-(4.2) será analizada en la siguiente sección.
Modelar un sistema físico en la forma de perturbaciones singulares puede no ser sencillo. No
siempre es evidente cómo elegir los parámetros que pueden considerarse “pequeños”. En muchas
aplicaciones, el conocimiento de los procesos físicos y de los componentes del sistema es de gran
ayuda. Los siguientes ejemplos muestran algunos casos típicos. En el primer ejemplo, el parámetro
ε es una pequeña constante de tiempo. Esta es la fuente más popular de modelos en perturbaciones

2
Fig. 4.1: Esquema electromecánico del sistema del Ejemplo 4.1.
singulares, y la que históricamente despertó el interés por este tipo de problemas. En el segundo
ejemplo se reformula el problema anterior para que el parámetro de perturbación sea adimensional.
Pequeñas constantes de tiempo, masas, capacitancias, y demás elementos “parásitos” que incrementan
el orden del modelo son muy comunes en el modelado de sistemas físicos; frecuentemente
estos elementos parásitos se ignoran o desprecian para reducir la complejidad del problema. El
tercer ejemplo se modela un circuito eléctrico que muestra que eliminar apriorielementos parásitos
puede tener graves consecuencias. El método de perturbaciones singulares legitimiza esta
simplificación ad hoc, y provee herramientas para mejorar los modelos que han sido simplificados
de más. En el cuarto ejemplo ε es el recíproco una ganancia elevada en un sistema realimentado, y
representa una fuente importante de modelos singularmente perturbados. En el diseño de sistemas
de control realimentado es muy frecuente el empleo de parámetros que se hacen tender asintóticamente
a infinito (también conocidos como parámetros de “alta ganancia”). Una aproximación
típica de tales sistemas es modelarlos en la forma de perturbaciones singulares. El quinto ejemplo,
si bien no está relacionado directamente con la técnica de perturbaciones singulares, muestra que
a veces una realimentación de alta ganancia puede desmejorar el desempeño del sistema. En el
sexto ejemplo el parámetro ε es una resistencia parásita en un circuito eléctrico. Despreciar este
elemento parásito reduce el orden del modelo pero de manera muy distinta al caso estudiado en
el primer ejemplo, y para expresarlo en la forma típica de perturbaciones singulares las variables
de estado se deben elegir cuidadosamente. Finalmente, en el séptimo ejemplo el parámetro ε es la
relación entre las frecuencias naturales de oscilación de la carrocería y de la rueda en un modelo
de la suspensión de un automóvil. La característica distintiva de este sistema es que no puede
expresarse en la forma típica sin escalar las variables de una forma dependiente de ε.
Ejemplo 4.1 Motor de corriente continua controlado por armadura
Un motor de corriente continua controlado por armadura (4.1) se puede modelar por el sistema de ecuaciones
de estado de segundo orden
J dω = ki,
dt
L di = −k ω − Ri+ u,
dt
donde i, u, R, y L son la corriente de armadura, tensión de alimentación, resistencia e inductancia, J
es el momento de inercia del a carga, ω es la velocidad angular, y ki y kw son el torque y la fuerza
contraelectromotriz, respectivamente, que se obtienen con una excitación de flujo constante. La primera
ecuación de estado es una ecuación mecánica de torque, y la segunda es la ecuación del transitorio eléctrico
en el circuitos de armadura. En general, la inductancia L es pequeña, y juega el rol del parámetro ε. Esto
significa que, con ω = x y i = z el modelo del motor está en la forma típica (4.1)-(4.2) con f(t, x, y, ε) =
f(t, ω,i,ε) =ki, y g(t, x, y, ε) =g(t, ω,i,ε) =−k ω − Ri+ u siempre que R 6= 0. Despreciando L, se
resuelve
0=g(t, x, y, 0) = −k ω − Ri+ u,
para obtener la únca raíz z = h(t, x)
i = u − kω
R .
El modelo lento se obtiene al sustituir la ecuación anterior en la ecuación del torque mecánico,
J ˙ω = − k2
R ω + k R u
que es el modelo habitual de primer orden del motor de corriente continua. 2

4.2. EL MODELO TÍPICO DE PERTURBACIONES SINGULARES 3
Fig. 4.2: Circuito eléctrico con diodo túnel. Esquemático (a) . Modelo linealizado (b) .
Ejemplo 4.2 Motor de corriente continua controlado por armadura (modelo adimensional)
En general es preferible reformular el modelo de manera que el parámetro ε resulte adimensional. A tal fin
se definen las variables adimensionales
ω r = ω Ω , i r = R kΩ i = i , u r = u
i 0 kΩ ,
ysereescribenlasecuacionesdeestadocomo
JR dω
k 2 Ω dt = R kΩ i, ⇒ T dω r
m
dt
= i r ,
L R di
R kΩ dt = − k
kΩ ω − R kΩ i + 1
kΩ u, ⇒ T di r
e
dt
= −ω r − i r + u r ,
donde T m = JR/k 2 es la constante de tiempo mecánica, y T e = L/R es la contante de tiempo eléctrica.
Como T m À T e , se elige T m como la unidad de tiempo: se define una nueva variable adimensional t r = t/T m
ysereescribenlasecuacionesdeestadocomo
dω r
dt r
= i r ,
T e di r
T m dt r
= −ω r − i r + u r.
Este escalado permite expresar el modelo en la forma típica, donde el parámetro ε es un parámetro adimensional
ε = Te
= Lk2
T m JR 2
que depende de las distintas constantes físicas del sistema. Además, desde el punto de vista del análisis, el
modelo adimensional es función de un único parámetro ε, mientras que el modelo del Ejemplo 4.1 intervienen
cuatro parámetros (J, k, L, R). 2
Ejemplo 4.3 Circuito eléctrico con diodo túnel
En el circuito eléctrico de la Fig. 4.2(a) el punto de polarización se elige de modo que el modelo de pequeña
señal del diodo túnel es una resistencia negativa en paralelo con una capacidad parásita de valor C d
[Fig. 4.2(b)]. Las ecuaciones de nodo del circuito son
dv 1
C d
dt − 1 v 1 + 1 v 1 − 1 v 2
R d R 2 R 2
= 0,
1
v 2 − 1 dv 2
v 1 + C 1
R 2 R 2 dt + i = 0,
iR 1 + di
dt L − v 2 = 0.
Como el capacitor parásito C d es pequeño se lo adopta como parámetro de perturbación, C d = ε. Eligiendo
como es usual las tensiones en los capacitores y la corriente en la inductancia como variables de estado,
x 1 = i, x 2 = v 2, z = v 1 se tiene que el modelo dinámico del sistema linealizado de pequeña señal es
⎛
⎛ ⎞
ẋ 1
⎝ ẋ 2
⎠ =
εż ⎜
⎝
− R 1
L 1
1
L 1
0
− 1 C 1
− 1
R 2 C 1
1
0
1
R 2
R 2 C 1
R 2 − R d
R 2R d
⎞
⎛
⎝
⎟
⎠
x 1
x 2
z
⎞
⎠ .

4
Fig. 4.3: Sistema con realimentación de alta ganancia. Modelo nominal (a) . Modelo reducido o lento (b) .
El modelo se puede normalizar eligiendo x 1r = i/i 0 ,x 2r = v 2 /(i 0 R 1 ),z r = v 1 /(i 0 R 1 ), y reescalando el
tiempo como t =(R 2 C 1 )t r . Se tiene entonces
⎛ dx 1r
⎞ ⎛
dt r
dx 2r
⎜ dt r
=
⎟
⎝
ε dz ⎠ ⎜
⎝
r
dt r
− τ 2
τ 1
τ 2
τ 1
0
− R2
R 1
−1 1
0 1
⎞
⎛
⎜
⎝
R
⎟
2
− 1
⎠
R d
donde τ 1 = L/R 1 , τ 2 = C 1 R 2 , y el parámetro de perturbación es ε = C d /C 1 . 2
Ejemplo 4.4 Realimentación de alta ganancia
El sistema de control que se muestra en la Fig. 4.3(a) tiene un lazo de realimentación interna para linealizar
el comportamiento del actuador, donde en general la ganancia k 1 del integrador es grande. La planta es un
sistema de una entrada y una salida (SISO) representado por el modelo de estado
ẋ p = Ax p + bu p ,
y = cx p .
donde los vectores x, b, c ylamatrizA tienen las dimensiones apropiadas. El actuador no lineal ψ(·)
pertenece al sector [0, ∞), es decir ψ(0) = 0, y ψ(y) > 0 para todo y 6= 0. Lasecuacionesdelsistemade
lazo cerrado son
ẋ p = Ax p + bu p,
1
˙u p = ψ(u − u p − k 2 cx p ).
k 1
Definiendo ε =1/k p ,x p = x, u p = z, el modelo toma la forma del modelo típico (4.1)-(4.2). Haciendo
ε =0, o k 1 →∞, se resuelve
ψ(u − u p − k 2 cx p )=0
para obtener
u p = u − k 2 cx p
que es la única raíz pues ψ(.) se anula sólo en el origen. El modelo reducido (o lento) es
ẋ p =(A − k 2bc)x p + bu,
que está representado por el diagrama bloque simplificado de la Fig. 4.3(b), donde todo el lazo interno se
reemplaza por una conexión directa. 2
En este caso, el empleo de un lazo de realimentación interno de alta ganancia permite linealizar el
actuador. La alta ganancia hace que el lazo interno sea rápido y que su salida u p copie la entrada
u − k 2 y casi instantáneamente. Sin embargo, algunas veces se obtienen resultados inesperados
como muestra el siguiente ejemplo (Sussmann y Kokotović, 1991; Sepulchre et al, 1997).
Ejemplo 4.5 Problemas de la realimentación con alta ganancia
El sistema no lineal
ẋ = − 1 2 (1 + ξ 2) x 3 , x(0) = x 0
x 1r
x 2r
z r
⎞
⎟
⎠

4.2. EL MODELO TÍPICO DE PERTURBACIONES SINGULARES 5
Fig. 4.4: Circuito eléctrico del Ejemplo 4.6 (a) . Modelo simplificado cuando R C =0.
está conectado en cascada con el sistema lineal dado por
˙ξ 1 = ξ 2
˙ξ 2 = u.
atravésdelavariableξ 2 . El origen x =0del subsistema no lineal es globalmente asintóticamente estable para
cualquier condición inicial x 0 si |ξ 2 (t)| < 1 para todo t. El estado ξ 2 del sistema lineal puede interpretarse
como una perturbación aditiva en el sistema no lineal, y su estructura induce a pensar que si ξ 2 tiende a cero
rápidamente, el término ξ 2 x 3 es “menos desestabilizante”. Se puede hacer que ξ 2 (t) decaiga velozmente
aplicando una realimentación lineal de estados u = −2aξ 1 − a 2 ξ 2 ,quecona>0 ubica los dos polos del
subsistema lineal en (−a) . Si a es grande, el decaimiento exponencial de ξ 1 (t) , ξ 2 (t) es rápido, y el análisis
“intuitivo” indica que cuanto mayor sea a más rápidamente ξ 2 (t) → 0, y entonces pareciera que el dominio
de atracción de la cascada (con la realimentación del subsistema lineal) crece a medida que a →∞.
Sin embargo esto no es lo que ocurre. La solución explícita del subsistema no lineal es
x (t) =
x 0
q
1+[t + R , x(0) = x 0 .
t
ξ 0 2 (τ) dτ]x2 0
Para que exista solución, el argumento del radical no debe anularse para ningún t>0, ya que en caso
contrario x (t) →∞para algún t finito. En particular, la salida ξ 2 (t) del sistema lineal con condiciones
iniciales ξ 1 (0) = 1, ξ 2 (0) = 0 es ξ 2 (t) =−a 2 te −at , que alcanza un máximo ξ 2M = −a/e en t p =1/a.
Para esta solución ξ 2 (t) la expresión de x (t) es
x (t) =
x 0
p
1+[t +(1+at)e
−at
− 1]x 2 0
yenparticular,parat = t p ,
x(t p )=
x 0
p .
1+(a
−1
+2e −1 − 1)x 2 0
Si la ganancia a es tal que
x 2 0
a>
x 2 0 (1 − (4.6)
2e−1 ) − 1
el radicando es negativo, lo que indica que x(t p ) no existe pues x(t) →∞antes de t p =1/a. De modo
que el comportamiento “intuitivo”, que sugería emplear valores elevados de a, en realidad empeora el
comportamiento haciendo que la solución explote antes de un tiempo t p = a −1 . También es evidente que
a medida que se eligen valores de a más elevados, el rango de condiciones iniciales x 0 admisibles debe
reducirse para evitar la desigualdad (4.6). En otras palabras, el tamaño del dominio de atracción se reduce
cuando a crece. 2
Ejemplo 4.6 Circuito eléctrico en paralelo
El circuito eléctrico de la Fig. 4.4(a) se puede modelar por las ecuaciones diferenciales
C ˙v 1 = 1 R (E − v 1) − ψ(v 1 ) − 1 (v 1 − v 2 ),
R C
C ˙v 2 = 1 1
(E − v2) − ψ(v2) − (v 2 − v 1).
R R C
Si se considera R C como el parámetro ε, hacer ε =0(reemplazar R C por un cortocircuito) es equivalente a
conectar los dos capacitores en paralelo; en un modelo bien formulado deberían quedar reemplazados por un

6
único capacitor equivalente y el modelo simplificado queda de primer orden. Para representar la reducción
de orden como una perturbación singular, se reescriben las ecuaciones de estado como
ε ˙v 1 =
ε
RC (E − v 1) − ε C ψ(v 1) − 1 C (v 1 − v 2 ),
ε ˙v 2 =
ε
RC (E − v 2) − ε C ψ(v 2) − 1 C (v 2 − v 1 ).
Si el modelo estuviese en la forma típica (4.1)-(4.2), tanto v 1 como v 2 deberían considerarse como las
variables z, y la condición (4.3) resultaría
v 1 − v 2 =0.
Las raíces de esta ecuación no están aisladas, que viola la hipótesis básica sobre las raíces de (4.3). En
consecuencia, la elección de v 1 y v 2 como variables de estado no permite expresar el modelo en la forma
típica. Sin embargo, eligiendo
x = 1 (v 2 1 + v 2 ), z = 1 (v 2 1 − v 2 ),
las ecuaciones de estado en las nuevas variables resultan
1
1
ẋ = (E − x) − [ψ(x + z)+ψ(x − z)],
RC
µ
2C
ε
εż = −
RC + 2
z −
ε [ψ(x + z) − ψ(x − z)].
C 2C
Ahora, la única raíz de g(t, x, z, ε) =0es z =0, que resulta en el modelo reducido
ẋ = 1
RC (E − x) − 1 C ψ(x).
Este modelo se representa en la Fig. 4.4(b), donde cada par de ramas equivalentes en paralelo se reemplaza
por una única rama. Para obtener ε como un parámetro adimensional, se normalizan x, z, y ψ como
x r = x E , z r = z E , ψ r (v) = R E ψ(Ev)
y se normaliza la variable temporal como t r
singulares en forma típica
= t/RC. Se obtiene entonces el modelo de perturbaciones
dx r
dt r
= 1− x r − 1 2 [ψ r (x r + z r )+ψ r (x r − z r )],
ε dz r
dt r
= −(ε +2)z r − ε 2 [ψ r(x r + z r ) − ψ r (x r − z r )],
donde el parámetro ε = R c/R es adimensional. 2
Ejemplo 4.7 Modelo de la suspensión de un automóvil
La Fig. 4.5(a) muestra un modelo del mecanismo de suspensión de un automóvil, donde m a,m c son las
masas del auto y de la rueda, k a y k r son las constantes elásticas del resorte del amortiguador y de la rueda,
b a es la constante de fricción viscosa del amortiguador, y F esunafuerzageneradaporunactuadorqueestá
presente en las suspensiones activas o semiactivas. Las distancias d a ,d r y d c son las elevaciones del autor,
la rueda y la superficie de la carretera, respectivamente, respecto de un punto de referencia. De acuerdo a
laleydeNewton,elbalancedefuerzasqueactúansobrem a y m r resulta en las ecuaciones
m a ¨da + b a( d ˙ a − d ˙ r)+k a(d a − d r) = F,
m r ¨dr + b a ( d ˙ r − d ˙ a )+k a (d r − d a )+k r (d r − d c ) = −F.
En un auto promedio, la frecuencia natural de oscilación de la rueda p k r/m r es alrededor de 10 veces la
frecuencia natural de oscilación del cuerpo del auto p k a /m a . Se define entonces el parámetro
s r
k a /m a ka m r
ε = = .
k r /m r k r m a
Este sistema masa-resorte es interesante porque no puede expresarse en la forma de perturbaciones singulares
típicas sin efectuar un escalamiento dependiente de ε. La rigidez de la rueda k r = O(1/ε 2 ) tiende a infinito
cuando ε → 0. Para que la energía potencial de la rueda k r (d r − d c ) 2 /2 quede acotada, el desplazamiento

4.3. PROPIEDADES TEMPORALES DEL MODELO TÍPICO 7
Fig. 4.5: Modelo de la suspensión de un automóvil. Modelo completo (a) y reducido (b) .
d r − d c debe ser de O(ε); esto es, el desplazamiento escalado (d r − d c )/ε debe permanecer finito. Además
de este escalamiento, se normalizan todas las variables para obtener un modelo adimensional. Las distancias
se dividen por un factor `, las velocidades por `pk
a /m a , las fuerzas por `k a yeltiempopor p m a /k a . En
consecuencia, para expresar el sistema en la forma de perturbaciones singulares típicas, se introducen las
variables lentas y rápidas
⎛
d a − d
⎞ ⎛
r
d r − d
⎞ c
ε
x = ⎜
⎝ d˙
r ⎟
a ma
⎠ , z = ε`
⎜
⎝ ˙
r ⎟
d r ma
⎠
` k a
` k a
y se considera que u = F/(k a`) es la entrada de control, w =(˙ d r /`) p m a /k a como una entrada de
perturbación, y t r = t p m a /k a como el tiempo normalizado. El modelo de perturbaciones singulares
resultante es
dx 1
= x 2 − z 2,
dt r
dx 2
= −x 1 − β(x 2 − z 2 )+u,
dt r
ε dz 1
dt r
= z 2 − w,
ε dz 2
dt r
= αx 1 − αβ(z 2 − x 2 ) − z − αu,
con
r
kam a
α = ,
k rm r
β = √ ba
. kam a
En los autos promedios, con suspensión pasiva, α ∈ [0.6, 1.2], β ∈ [0.5, 0.8], ε ∈ [0.08, 0.135]. Para el caso
de suspensiones activas o semiactivas, la constante de amortiguamiento puede reducirse porque la acción del
actuador se puede controlar de manera de proveer amortiguamiento adicional. Haciendo ε =0se obtiene
el modelo reducido
dx 1
dt r
= x 2 − w,
dx 2
dt r
= −x 1 − β(x 2 − w)+u,
que corresponde al modelo simplificado de un grado de libertad que se muestra en la Fig. 4.5(b). 2
4.3 Propiedades temporales del modelo típico
La respuesta ante estímulos externos de un sistema dinámico modelado con perturbaciones singulares
está caracterizada por la presencia de transitorios rápidos y lentos. La respuesta lenta

8
es aproximadamente la respuesta del sistema reducido (4.5), mientras que la diferencia entre esta
respuesta y la del modelo completo (4.1)-(4.2) es la respuesta rápida.
El problema típico de perturbaciones singulares se representa con el sistema de ecuaciones
ẋ = f(t, x, z, ε), x(t 0 )=x 0 (ε), (4.7)
εż = g(t, x, z, ε), z(t 0 )=z 0 (ε), (4.8)
donde las condiciones iniciales x 0 (ε), z 0 (ε) dependen suavemente de ε y t 0 ∈ [t 0 ,t 1 ). Las soluciones
del problema completo (4.7)-(4.8) se notarán como x(t, ε) y z(t, ε). Aldefinir el problema correspondiente
al modelo reducido (4.5), sólo se pueden especificar n condiciones iniciales; naturalmente,
se retiene el estado inicial de x para obtener el problema reducido
ẋ = f[t, x, h(t, x), 0], x(t 0 )=x 0 = x 0 (0). (4.9)
La solución de (4.9) se notará como ¯x(t). Como las variables z han sido excluidas del modelo
reducido y reemplazadas por su “estado casi estacionario” h(t, x), la única información que puede
obtenerse sobre z después de haber resuelto (4.9) es calcular
¯z = h[t, ¯x(t)]
que describe el comportamiento casi estacionario de z cuando x(t) =¯x(t). En contraste con el
comportamiento de la variable original z(t), que comienza en t 0 con un valor z(t 0 )=z 0 (ε), la
variable ¯z(t) de estado casi estacionario no es libre de tomar un valor arbitrario en t 0 , y puede
haber una gran diferencia entre su valor inicial ¯z(t 0 )=h[t 0 , ¯x(t 0 )] = h[t 0 ,x(t 0 )] = h(t 0 ,x 0 ) yel
estado inicial de la variable z, dado por z(t 0 )=z 0 (ε). Entonces ¯z(t) no puede ser una aproximación
uniforme de z(t, ε); lo mejor que puede esperarse es que la estimación
z(t, ε) − ¯z(t) =O(ε)
se verifiqueenunintervaloqueexcluyeat 0 , esto es, para t ∈ [t b ,t 1 ] donde t b >t 0 . Por otra parte,
es razonable pensar que la estimación
x(t, ε) − ¯x(t) =O(ε)
sea uniformemente válida para todo t ∈ [t 0 ,t 1 ], ya que
x(t 0 , ε) − ¯x(t 0 )=x 0 (ε) − x 0 (0) = O(ε).
Si el error z(t, ε) − ¯z(t) es realmente O(ε) sobre [t b ,t 1 ], entonces debe ser cierto que durante el
intervalo inicial [t 0 ,t b ] la variable z(t) se aproxima a ¯z(t). La velocidad de aproximación puede ser
alta, pues ż = g(·)/ε. De hecho, eligiendo ε =0en(4.2)sehacequeeltransitoriodez(t) sea
instantáneo si g(·) 6= 0. Evidentemente, para que z(t) converja a su estado casi estacionario ¯z(t)
deben satisfacerse ciertas condiciones de estabilidad. Para efectuar este análisis es más conveniente
efectuar el cambio de variables
y = z − h(t, x) (4.10)
que desplaza el estado de casi equilibrio z al origen. En las nuevas variables (x, y), el problema
completo es
ẋ = f[t, x, y+h(t, x), ε], x(t 0 )=x 0 (ε), (4.11)
εẏ = g[t, x, y+h(t, x), ε]−ε ∂h
∂t −ε∂h ∂x f[t, x, y+h(t, x), ε], y(t 0)=z 0 (ε)−h[t 0 ,x 0 (ε)]. (4.12)
El estado casi estacionario de (4.12) es y =0, que cuando se sustituye en 4.11 resulta en el modelo
reducido (4.9). Para analizar (4.12), debe tenerse en cuenta que εẏ puede ser finita aún cuando
ε → 0 e ẏ →∞. Por eso es conveniente cambiar la escala de tiempo,
ε dy
dt = dy
dτ , de donde dτ
dt = 1 ε , (4.13)

4.3. PROPIEDADES TEMPORALES DEL MODELO TÍPICO 9
eligiendo τ =0como el valor inicial en t = t 0 . La nueva variable temporal τ =(t − t 0 )/ε permite
“ampliar” el nivel de detalle, ya que cuando ε tiende a cero τ tiende a infinito aún cuando t sea
ligeramente mayor que t 0 (siempre que esta diferencia sea independiente de ε). En la escala de
tiempo τ (4.12) se expresa como
dy
= g[t, x, y + h(t, x), ε] − ε∂h
dτ ∂t − ε∂h ∂x f[t, x, y + h(t, x), ε], y(0) = z 0(ε) − h[t 0 ,x 0 (ε)]. (4.14)
Las variables t, x en la ecuación anterior varían lentamente, pues en la escala de tiempo τ están
dadas por
t = t 0 + ετ, x(t) =x(t 0 + ετ).
Hacer ε =0“congela” estas variables en t = t 0 y x = x 0 , y reduce (4.14) al sistema autónomo
dy
dτ = g[t 0,x 0 ,y+ h(t 0 ,x 0 ), 0], y(0) = z 0 (0) − h[t 0 ,x 0 (0)] = z 0 − h(t 0 ,x 0 ) (4.15)
que tiene un equilibrio en y =0. Si este punto de equilibrio es asintóticamente estable y si y(0)
pertenece a su dominio de atracción, es razonable esperar que la solución de (4.15) alcance un
entorno O(ε) del origen durante el intervalo de acercamiento rápido [t 0 ,t b ]. Después de este
intervalo, se necesita una propiedad de estabilidad que garantice que y(τ) permanezca cerca del
origen mientras que las variables (t, x) lentamente variantes evolucionan desde sus estados iniciales
(t 0 ,x 0 ). Para analizar esta situación se permite que los parámetros congelados tomen valores en
la región donde viven las variables (t, x) lentamente variantes. Se verá en el Capítulo 5 que si el
origen de (4.15) es exponencialmente estable, uniformemente en los parámetros congelados (t 0 ,x 0 ),
entonces permanece exponencialmente estable cuando estos parámetros se cambian por las variables
(t, x) lentamente variantes.
Si se supone que la solución ¯x(t) del problema reducido está definida para t ∈ [t 0 ,t 1 ], y ¯x(t) ∈ X ⊂
R n para algún conjunto abierto X. Se puede reescribir (4.15) como
dy
= g[t, x, y + h(t, x), 0] (4.16)
dτ
donde t ∈ [t 0 ,t 1 ] y x ∈ X se tratan como parámetros fijos. La ecuación (4.16) se denomina modelo
osistemadecapa límite. A veces esta definición se utiliza para designar a (4.15), aunque esto no
debe causar confusión porque (4.15) es una evaluación de (4.16) para un tiempo y un estado inicial
dados. La propiedad de estabilidad crucial para este problema es la estabilidad exponencial del
origen uniformemente en los parámetros “congelados”, que se define a continuación.
Definición 4.1 Estabilidad exponencial uniforme. El punto de equilibrio y =0del sistema
de capa límite
dy
= g[t, x, y + h(t, x), 0]
dτ
es exponencialmente estable, uniformemente para t ∈ [t 0 ,t 1 ],x∈ X si existen constantes positivas
k, γ y ρ 0 tal que sus soluciones satisfacen
ky(τ)k ≤ k ky(0)k e −γτ , para todo τ ≥ 0, (4.17)
yparatodoky(0)k < ρ 0 ,t∈ [t 0 ,t 1 ],x∈ X. 4
Aparte de unos pocos casos aislados donde la solución del problema de capa límite puede conocerse
en forma exacta, la verificación de la estabilidad exponencial del origen puede hacerse por
linealización o por análisis de Lyapunov. Para el caso de sistemas autónomos (i.e. cuando g no
depende de t), se puede demostrar que si los autovalores de la matriz Jacobiana
J = ∂g
∂y

10
satisfacen
½ ∙ ∂g
Re λ [t, x, h(t, x), 0]¸¾
≤−c

4.3. PROPIEDADES TEMPORALES DEL MODELO TÍPICO 11
uniformemente para t ∈ [t 0 ,t 1 ], donde ȳ(τ) es la solución del problema de capa límite (4.15).
Además, dado cualquier t b >t 0 , existe un ε ∗∗ ≤ ε ∗ tal que z(t, ε) y ¯z = h[t, ¯x(t)] verifican
z(t, ε) − h[t, ¯x(t)] = O(ε) (4.21)
uniformemente para t ∈ [t b ,t 1 ] yparatodoε < ε ∗∗ . 2
La demostración del Teorema se basa en las propiedades de estabilidad del modelo de capa límite
para probar que
ky(t, ε)k ≤ k 1 e − α ε (t−t0) + εδ.
Esta cota se utiliza en (4.11) para probar (4.19), lo que es plausible, ya que R t
0 e−αs/ε ds es O(ε).
La prueba concluye con un análisis de error de (4.12) en la escala de tiempo τ para probar (4.20)
y (4.21).
Ejemplo 4.8 Motor de corriente continua controlado por armadura
El motor de corriente continua controlado por armadura del Ejemplo 4.1 tiene como modelo típico
ẋ = z, x(0) = x 0,
εż = −x − z + u(t), z(0) = z 0 .
Se supone que u(t) =t para t ≥ 0, y se desea resolver las ecuaciones de estado para t ∈ [0, 1]. En este
ejemplo es evidente que
f(t, x, z, ε) = z,
g(t, x, z, ε) = −x − z + t.
El modelo reducido. Para calcular el modelo reducido se hace ε =0, yseresuelve(4.3),i.e. g(t, x, z, 0) = 0;
la única raíz es
z(t) =h(t, x) =−x + t.
Modelo de capa límite (4.16). Efectuando el cambio de coordenadas y = z − h(t, x), se tiene
Después de efectuar el reescalado temporal,
y = z + x − t.
dy
dτ
= g{t 0 ,x(t 0 ),y+ h[t 0 ,x(t 0 )], 0}
= −x(t 0 ) − {y + h[t 0 ,x(t 0 )]} + t 0
= −x 0 − y − h[t 0,x(t 0)] + t 0
= −y
Evidentemente, el modelo de capa límite es globalmente exponencialmente estable. Las condiciones iniciales
son y 0 = z 0 − h(t 0 ,x 0 )=z 0 + x 0
Problema reducido. Está dado por (4.9)
Soluciones. La solución del problema reducido es
ẋ = f[t, x, h(t, x), 0], x(t 0 )=x 0 ,
= −x + t, x(0) = x 0 .
¯x(t) =t − 1+(1+x 0 )e −t .
mientras que la solución rápida de estado casi estacionario está dada por
La solución del problema de capa límite es
¯z(t) = h[t, ¯x(t)] = −¯x(t)+t
= 1− (1 + x 0)e −t .
y(τ) =(x 0 + z 0 )e −τ .

12
Fig. 4.6: Lugar de las raíces para el sistema del Ejemplo 4.8.
De acuerdo al Teorema 1,
x(t, ε) − ¯x(t) = x(t, ε) − [t − 1+(1+x 0 )e −t ]=O(ε),
z(t, ε) − h[t, ¯x(t)] − ȳ(t/ε) = z(t, ε) − [1 − (1 + x 0)e −t ] − [(x 0 + z 0)e −t/ε ]=O(ε),
En este caso se puede calcular la solución exacta ya que el sistema es lineal. Se tiene que
x(t, ε) = t − 1+(1+x 0) e −t
2ε
2ρ
donde ρ = √ 1 − 4ε, y
= t − 1+(1+x 0 )e −t
2ε
z(t, ε) = 1+ e −t
2ε
2ρ
= 1+ e −t
2ε
2ρ
h(ρ − 1)e −kρ
2ε
¡
cosh
kρ
¢ e −t
2ε
2ε +
2ρ
−kρ
[(1 − ρ)+2x0 + z0(1 + ρ)] e 2ε
i
kρ
+(ρ +1)e 2ε + ε(1 − z e −t
2ε
0)
³e kρ
2ε
ρ
£
(1 + x0 )sinh ¡ kρ
2ε
−
e −t
2ε
2ρ
£
−(1 + z0 )ρ cosh ¡ ¢
kρ +(1+2x0 + z
2ε
0 )sinh ¡ ¢¤
kρ
2ε
z(t, ε) ∼ = 1 − (1 + x0)e −t +(x 0 + z 0)e − t−εt
ε − ε (1 + 2x 0 + z 0)
´
−kρ
+ e 2ε
¢
+2ε(1 − z0 )cosh ¡ ¢¤
kρ
2ε
[(1 + ρ)+2x0 + z0(1 − ρ)] e
kρ
2ε
Si ε ¿ 1 se puede aproximar ρ = √ 1 − 4ε ∼ = 1 − 2ε, y 1/ρ =1/ √ 1 − 4ε ∼ = 1+2ε, y entonces,
´
x(t, ε) ∼ = t − 1+(1+x0)e −t + ε (x 0 + z 0)
³e −t − e − t−εt
τ + O(ε 2 ),
³e −t − e − t−εt
τ
´
+ O(ε 2 ),
De la expresión de estas soluciones se observa que se verifican las predicciones del Teorema.
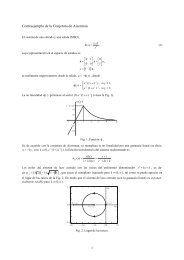
Como el sistema es lineal la doble escala de tiempo queda en evidencia a partir de los polos del sistema. En
este caso,
µ µ µ µ
ẋ 0 1 x 0
=
+ u(t)
ż −1/ε −1/ε z 1/ε
cuyos autovalores son
λ 1 = −1+√ 1 − 4ε
= −1 − ε − 2ε 2 − 5ε 3 + ···,
2ε
λ 2 = −1 − √ 1 − 4ε
= − 1 2ε
ε − ¡ −1 − ε − 2ε 2 − 5ε 3 + ···¢ .
Se observa que cuando ε → 0 el polo “lento” λ 1 tiende a (−1), mientras que el polo rápido λ 2 tiende a
(−∞). La Fig. 4.6 muestra el lugar de las raíces del sistema. 2
Ejemplo 4.9 Circuito eléctrico con diodo túnel
El modelo reducido del circuito adimensional del Ejemplo 4.3 se obtiene haciendo ε =0. Se tiene entonces
que
z r = h(t r ,x r )=−
R d
x 2r ,
R 2 − R d

4.3. PROPIEDADES TEMPORALES DEL MODELO TÍPICO 13
y entonces el modelo reducido es
⎛
⎜
⎝
dx 1r
dt r
dx 2r
dt r
⎞ ⎛
⎟
⎠ = ⎜
⎝
− τ 2
τ 1
τ 2
τ 1
− R 2
R 1
⎞
µ ⎟ x1r
R d ⎠
R 2 − R d
.
x 2r
Para encontrar el modelo de capa límite se efectúa el cambio de coordenadas y = z r − h(t r,x r) de donde
resulta
dy
dτ
= g[t r,x r,y+ h(t r,x r), 0]
= x 2r + R µ
2 − R d
y −
R d
R
d
x 2r =
R 2 − R d
µ
R2
Rd − 1
y.
Si R 2 >R d el modelo de capa límite es inestable: en estas condiciones el comportamiento del sistema
completo no puede estudiarse a partir del modelo reducido. Respecto de este último, la matriz característica
es Hurwitz (es decir, tiene todos sus autovalores con parte real negativa) si la traza es negativa y el
determinante positivo, i.e.
de donde resulta
τ = − τ 2
τ 1
+
R d
R 2 − R d
< 0, ∆ = τ 2
τ 1
µ
R2
R 1
−
R 2
R d
R
d
> 0
R 2 − R d
< < τ 2
.
R 1 R 2 − R d τ 1
Como R 1 ,R 2 , τ 1 , τ 2 son parámetros positivos, para que el modelo reducido sea estable es necesario que
al menos R 2 >R d . Esta condición es la de inestabilidad del modelo de capa límite; en consecuencia, el
comportamiento del sistema reducido no se aproxima al del sistema completo. Este ejemplo muestra que
despreciar aprioriel efecto de elementos parásitos puede tener serias consecuencias: en base al análisis con
el sistema “simplificado” (reducido) se puede pensar que el sistema “real” es estable cuando en realidad es
inestable. 2
Ejemplo 4.10 Realimentación de alta ganancia
El modelo de perturbaciones singulares del Ejemplo 4.4 es
ẋ = Ax + bz, x(0) = x 0,
εż = ψ[u(t) − z − k 2 cx], z(0) = z 0 ,
donde se supone que u(t) =1para t ≥ 0, y ψ(·) = arctan(·). La única raíz de (4.3)es
yelmodelodecapalímite(4.16)es
z(t) =h(t, x) =1− k 2 cx,
dy
=arctan(−y) =− arctan(y).
dτ
El Jacobiano es
J = ∂g
¯ = − 1 = −1,
∂y
¯y=0
1+y
¯¯¯¯y=0 2
que muestra que el origen del modelo de capa límite es localmente exponencialmente estable; también es
globalmente asintóticamente estable. Como el problema reducido
ẋ =(A − k 2 bc)x + b · 1, x(0) = x 0 ,
es lineal, es evidente que se satisfacen las hipótesis del Teorema 1, y entonces es válido aproximar las
soluciones de x(t, ε) ydez(t, ε) en función de los modelos reducidos y de capa límite, respectivamente. 2

14
Fig. 4.7: Modelo de capa límite para el sistema del Ejemplo 4.11: z 1 = h 1 (t, x) = −(1 + t)x (a);
z 2 = h 2 (t, x) =0(b) y z 3 = h 3 (t, x) =(1+t) (c) .
Ejemplo 4.11 Sistema no autónomo
Para el sistema no lineal y no autónomo
ẋ =(1+t) x2
,
z
x(0) = 1,
εż = −[z +(1+t)x]z[z − (1 + t)], z(0) = z 0,
al obtener el modelo reducido haciendo ε =0se encuentra que la ecuación
0=g(t, x, z, 0) = −[z +(1+t)x]z[z +(1+t)x]
tiene tres raíces aisladas
z 1 = −(1 + t)x, z 2 =0, z 3 =(1+t).
en la región t ≥ 0, x>k,donde 0

4.3. PROPIEDADES TEMPORALES DEL MODELO TÍPICO 15
con condiciones iniciales y(0) = z 0 + x 0 = z 0 +1. El origen y =0de este sistema el localmente
exponencialmente estable, pues
J = ∂g 1
¯ = −3y 2 +6y − = −2.
∂y
2¯¯y=0 ¯y=0
y su región de atracción está dada por las condiciones iniciales que satisfacen y(0) < 1, obienque
z 0 < 0.
• Para la raíz z 2 = h 2 (t, x) =0, el modelo de capa límite es
dy
= g2[t, x, y + h2(t, x), 0]
dτ
= −[y +(1+t)x]y[y − (1 + t)]
Un gráfico de la función del miembro derecho se muestra en la Fig. 4.7(b) que muestra que el origen
y =0es inestable. En consecuencia no se puede aplicar el Teorema 1.
• Para la raíz z 3 = h 3 (t, x) =1+t, el modelo de capa límite (4.16) es
dy
= g3[t, x, y + h3(t, x), 0]
dτ
= −[y +(1+t)+(1+t)x][y +(1+t)]y.
El gráfico de la función del miembro derecho se ilustra en la Fig. 4.7(c); de manera similar al primer
caso, se puede demostrar que el origen y =0es localmente exponencialmente estable. El modelo
reducido es
ẋ =(1+t) x2
¯ = x 2 , x(0) = 1,
z
¯z=(1+t)
que tiene como solución
¯x(t) = 1
1 − t ,
para todo t ∈ [0, 1). Aunque la solución tiene un tiempo de escape finito en t =1, el Teorema 1 sigue
siendo válido sobre un intervalo [0,t 1], donde t 1 < 1. El problema de capa límite con t =0,x=1es
dy
dτ = −(y +2)(y +1)y, y(0) = z 0 − h 3 (t 0 ,x 0 )=z 0 − 1,
que es localmente exponencialmente estable pues
J = ∂g3
∂y
¯ = −3y 2 − 6y − = −2
2¯¯y=0 ¯y=0
y su región de atracción está dada por las condiciones iniciales que satisfacen y(0) > −1, obienque
z 0 > 0.
De las tres raíces de (4.3) sólo dos de ellas,
z 1 = h 1(t, x) =−(1 + t)x
y
z 3 = h 3 (t, x) =1+t
permiten obtener modelos reducidos válidos. El teorema de Tikhonov (1) se aplica a la raíz h 1 (t, x) si
z 0 < 0 yalaraízh 3 (t, x) si z 0 > 0.
Las Fig. 4.8 ilustran los resultados de simulaciones para ε =0.1. La Fig. 4.8(a) muestralaevoluciónde
la solución exacta z(t, ε) y de la solución aproximada ¯z(t) para cuatro condiciones iniciales: z (1)
01 = −2,
z (1)
02 = −3/10 para el modelo reducido asociado a z1 y z(3) 01 =2,z(3) 02 =1/2 para el modelo reducido
asociado a z 3 . Lastrayectoriasmuestranclaramenteladoble escala de tiempo: comienzan con un rápido
transitorio de z(t, ε) desde z 0 hacia ¯z(t), y luego permanecen en un entorno de ¯z(t). Para la condición inicial
z (1)
02 = −3/10 la convergencia a ¯z(t) no se alcanza en el intervalo de tiempo que se muestra en la figura. El
mismo caso se muestra en la Fig. 4.8(b) sobre un intervalo de tiempo mayor, donde se observa que z(t, ε)
se aproxima a ¯z(t). En la Fig. 4.8(a) es evidente la aproximación asintótica O(ε) resultante del Teorema de
Tikhonov. 2

16
Fig. 4.8: Resultados de simulación del sistema del Ejemplo 4.11. Soluciones rápidas exactas z(t, ε) y
aproximadas ¯z(t) para ε =0.1 y cuatro condiciones iniciales distintas: z (1)
01 = −2, z(1) 02 = −0.3, z(3) 01 =2,
z (3)
02 = 0.5 (a) . Soluciones exactas z(t, ε), x(t, ε) y aproximadas ¯z(t), ¯x(t) para ε = 0.1, y x(0) = 2,
z(0) = z (1)
02 = −0.3 (b) .
4.4 Variedades rápidas y lentas
En esta sección se estudia el comportamiento en dos escalas de tiempo desde un punto de vista
geométrico, como trayectorias en R n+m . Una variedad k-dimensional en R n (1 ≤ k ≤ n)
es un objeto matemático bien definido. Para los finesdeesteapunteessuficiente pensar que
una variedad k-dimensional es la solución de una ecuación η(x) = 0, donde η : R n → R n−k
es suficientemente suave (esto es, varias veces continuamente diferenciable). Por ejemplo, el
círculo unitario {(x 1 ,x 2 ) ∈ R 2 : x 2 1 + x 2 2 = 1} es una variedad 1-dimensional en R 2 . La esfera
unitaria {(x 1 ,...,x n ) ∈ R n : P n
i=1 x2 i = 1} es una variedad (n − 1)-dimensional en R n .
Una variedad {η(x) = 0} es una variedad (positiva) invariante para el sistema ẋ = f(x) si
η[x(t 0 )] = 0 ⇒ η[x(t)] ≡ 0 para todo t ≥ t 0 . En otras palabras, si la condición inicial en t = t 0 está
sobre la variedad, la solución permanece sobre la variedad para todo t ≥ t 0 .
Para poder trabajar con variedades invariantes, se restringe el estudio al caso de sistemas autónomos,
y para simplificar la notación se supone que f(·) y g(·) son independientes de ε. Por lo tanto
se considera la siguiente forma más simple del problema de perturbaciones singulares (4.1)-(4.2):
ẋ = f(x, z), (4.22)
εż = g(x, z). (4.23)
Cuando ε =0,z= h(x) es una raíz aislada de 0=g(x, z) que satisface las hipótesis del Teorema
1. La ecuación z = h(x) describe una variedad n-dimensional en el espacio (m + n)-dimensional
de (x, z), y es una variedad invariante del sistema
ẋ = f(x, z), (4.24)
0 = g(x, z), (4.25)
pues una trayectoria de (4.24)-(4.25) que comienza en la variedad z = h(x) permanece en ella para
todo t ≥ t 0 para el cual la solución esté definida. El comportamiento sobre esta variedad queda
descrito por el modelo reducido
ẋ = f[x, h(x)].
El Teorema 1 demuestra que las trayectorias de (4.22)-(4.23), que comienzan en un entorno O(ε)
de z = h(x) permanecerán dentro de ese entorno.
Este comportamiento motiva la siguiente pregunta: ¿Existe un análogo de la variedad invariante
para el caso en que ε > 0? Resulta que, bajo las hipótesis del Teorema 1, existe una variedad
invariante para el sistema (4.22)-(4.23) que yace a una distancia O(ε) de la variedad z = h(x). La
idea es encontrar un invariante para (4.22)-(4.23) de la forma
z = H(x, ε) (4.26)

4.4. VARIEDADES RÁPIDAS Y LENTAS 17
donde H(·) es una función suficientemente suave de x ydeε. La expresión (4.26) define una
variedad n-dimensional, dependiente de ε, en el espacio (n + m) dimensional de (x, z). Para que
z = H(x, ε) sea una variedad invariante de (4.22)-(4.23), se debe verificar que
z(0, ε) − H[x(0, ε), ε] =0⇒ z(t, ε) − H[x(t, ε), ε] ≡ 0
para todo t ∈ J ⊂ [0, ∞), donde J es cualquier intervalo sobre el cual existe la solución [x(t, ε),
z(t, ε)]. Diferenciando ambos miembros de (4.26) respecto del tiempo, multiplicando por ε ysustituyendo
ẋ, εż y z por (4.22), (4.23) y (4.26), respectivamente, se obtiene la condición de la
variedad
0=g[x, H(x, ε)] − ε ∂H f[x, H(x, ε)] (4.27)
∂x
que H(x, ε) debe satisfacer para todo x en la región de interés, y para todo ε ∈ [0, ε 0 ]. En ε =0la
ecuación diferencial a derivadas parciales (4.27) degenera en
0=g[x, H(x, 0)],
que muestra que H(x, 0) = h(x). Como 0=g(x, z) puede tener más de una raíz aislada z = h(x)
se debe buscar un invariante para (4.22)-(4.23) en un entorno de cada raíz. Se puede demostrar
que existe un ε ∗ > 0 y una función H(x, ε) que satisface la condición de la variedad (4.27) para
todo ε ∈ [0, ε ∗ ] ytalque
H(x, ε) − h(x) =O(ε)
para x acotados. La variedad invariante z = H(x, ε) se denomina la variedad lenta para (4.22)-
(4.23). A cada variedad lenta corresponde un modelo “lento”
ẋ = f[x, H(x, ε)] (4.28)
que describe exactamente el comportamiento en esa variedad.
En la mayoría de los casos no se puede resolver exactamente la condición de la variedad (4.27),
pero se puede aproximar H(x, ε) arbitrariamente tan cerca como se desee utilizando una serie de
Taylor en un entorno de ε =0. El procedimiento se basa en sustituir en (4.27) una serie de Taylor
para H(x, ε),
H(x, ε) =H 0 (x)+εH 1 (x)+ε 2 H 2 (x)+···
y calculando H 0 (x), H 1 (x), etc. igualando los coeficientes de la misma potencia en ε. Esto requiere
que las funciones f(·), g(·) sean continuamente diferenciables en sus argumentos un número
suficiente de veces. Es evidente que H 0 (x) =H(x, 0) = h(x). La ecuación para H 1 (x) es
∂g[x, h(x)]
∂z
H 1 (x) = ∂h f[x, h(x)],
∂x
y tiene solución única si el Jacobiano ∂g/∂z en z = h(x) es no singular, situación que queda
implícita por la condición (4.18) impuesta a los autovalores. Lasecuacionescorrespondientesa
términos de orden superior también resultan lineales y resolubles si el Jacobiano ∂g/∂z es no
singular.
Para introducir la noción de una variedad “rápida”, se examinan (4.22)-(4.23) en la escala de
tiempo τ = t/ε. En ε =0,x(τ) ≡ x(0), mientras que z(τ) evoluciona según
∂z
∂τ = g[x(0),z]
aproximándose al equilibrio z = h[x(0)]. Este comportamiento describe trayectorias (x, z) en R n+m ,
que, para cada x(0) yacenenlavariedad“rápida”F x definida por x = x(0) = constante, y
rápidamente descienden a la variedad z = h(x). Para ε > 0 pero pequeño, las variedades rápidas
son foliaciones de soluciones aproximándose rápidamente a la variedad lenta.

18
Fig. 4.9: Esquema del plano de fase del Ejemplo 4.12. Modelo aproximado para ε =0(a) yexactopara
ε =0.1 (b) .
Ejemplo 4.12 Sistema de segundo orden
El sistema de segundo orden
ẋ = −x + z,
εż = arctan(1− z − x),
tiene un punto de equilibrio en (x, z) =(1/2, 1/2). Para ε =0, la única raíz de 0=g(x, z) = arctan(1 −
z − x) es z = h(x) =1− x, que es la variedad lenta. El modelo lento es entonces
ẋ = −2x +1,
que tiene un punto de equilibrio en x =1/2. Por lo tanto las trayectorias sobre la variedad lenta se dirigirán
hacia el punto P =(1/2, 1/2), como muestra la Fig. 4.12(a). Las variedades rápidas para ε =0son paralelas
al eje z, y las trayectorias se dirigen hacia la variedad lenta z =1− x. Con esta información es posible
construir un boceto aproximado del plano de fase del sistema. Por ejemplo, una trayectoria que comience en
el punto A se moverá verticalmente hasta colisionar con la variedad lenta z =1− x en el punto B. Desde
B la trayectoria se desliza sobre la variedad lenta hacia el punto de equilibrio P. De manera similar, para
una condición C, la trayectoria sigue una línea vertical hasta el punto D, y luego se desplaza hacia el punto
de equilibrio sobre la variedad lenta. Para ε 6= 0pero pequeño, el plano de fase del sistema será similar al
obtenido para ε =0, como se aprecia en la Fig. 4.12(b) calculada para ε =0.1. 2
Ejemplo 4.13 Sistema de van der Pol
La ecuación de van der Pol
d 2 y
− μ(1 − y 2 ) dy + y =0,
dt 2 1
dt 1
cuando μ À 1 se puede expresar en la forma típica de perturbaciones singulares efectuando el cambio de
coordenadas
x = − 1 dy
+ y − 1 μ dt 1 3 y3 , z = y,
escalando la variable temporal como t = t 1/μ, ydefiniendo ε =1/μ 2 :
ẋ = z,
εż = −x + z − 1 3 z3 .
Con el auxilio de otras herramientas estudiadas en el curso, se conoce que la ecuación de van der Pol tiene
un ciclo límite estable (aplicando el teorema de Poincaré-Bendixon), y que la amplitud de ese ciclo límite
es aproximadamente igual a 2 (en el sistemas de coordenadas y-ẏ), al menos para μ pequeño (ε grande)
utilizando los métodos de promediación de Krylov-Boguliubov o perturbacionales de Linstedt-Poincaré. El
enfoque basado en las perturbaciones singulares permite tener una estimación más precisa de la ubicación
del ciclo límite, aunque en otras coordenadas.
Para ε =0, lasraícesaisladasz = h(x) de 0=g(x, z) resultan de
0=−x + z − 1 3 z3 .

4.4. VARIEDADES RÁPIDAS Y LENTAS 19
Fig. 4.10: OsciladordevanderPol. Variedadlentaz = h(x) para ε =0(a) y esquema aproximado del
plano de fase (b) .
La curva −x + z − 1 3 z3 =0, la variedad “lenta” para ε =0, semuestraenlaFig.4.10(a). Parax

20
Fig. 4.11: Trayectorias en el plano de fase del oscilador de van der Pol para ε =0.1.
AB o CD, a las que se aproximan casi verticalmente. Una vez sobre la variedad lenta, las trayectorias se
mueven hacia la curva cerrada EBFCE, si no están ya sobre ella, y quedarán ciclando allí. El ciclo límite
exacto del oscilador de van der Pol estará ubicado en un entorno O(ε) de esta curva cerrada. El plano de
fase de la Fig. 4.11, calculado para ε =0.1 confirmaestapredicción.
El estudio simplificado (con ε =0) permite estimar fácilmente el período de la oscilación de la solución
periódica. La curva cerrada EBFCE tiene dos lados rápidos (BF y CE) ydoslentos(EB y FC).
Despreciando la duración de los transitorios rápidos (de B a F ydeC a E), se puede estimar el período de
la oscilación T = t EB + t FC. El intervalo de tiempo T EB puede estimarse a partir del modelo reducido
ẋ = z
0 = −x + z − 1 3 z3
Diferenciando la segunda ecuación respecto de t e igualando las expresiones para ẋ se obtiene la ecuación
diferencial
ż =
z
1 − z 2
de modo que
t EB =
Z tB
t E
dt =
z B Z=1
z E =2
(1/z − z) dz
= lnz − (1/2)z 2¯¯1 = −(1/2) − ln 2 + 2 = (3/2) − ln 2.
2
El intervalo de tiempo t FC puede calcularse de manera similar, y por la simetría del problema, t EB = t FC . Por
lo tanto el período aproximado de la oscilación del sistema de van der Pol es T =3−2ln2para ε pequeños.
Este período está calculado para el modelo escalado expresado en la forma típica de perturbaciones singulares,
donde la variable temporal está escalada por μ. Para el sistema en las variables originales, el período de
oscilación está dado aproximadamente por
T 1 =(3− 2ln2)μ
para μ grande. 2

4.5. PERTURBACIONES SINGULARES EN SISTEMAS LINEALES 21
4.5 Perturbaciones singulares en sistemas lineales
Cuando los sistemas singularmente perturbados son lineales, los resultados se pueden expresar en
función del espectro (conjunto de autovalores) de ciertas matrices. En esta sección se tratará con
sistemas de la forma
à ! à !à !
ẋ A11 A 12 x
=
(4.29)
εż A 21 A 22 z
donde x ∈ R n , y ∈ R m y las matrices A ij tienen dimensiones compatibles. Si se hace ε =0en
(4.29), la segunda ecuación resulta
0 = g(x, z) =A 21 x + A 22 y. (4.30)
Si A 22 no es singular las raíces de 0 = g(x, z) son aisladas, y además únicas. Entonces se puede
despejar y de (4.30),
z = −A −1
22 A 21x. (4.31)
Sustituyendo (4.31) en (4.29) se obtiene el sistema reducido
ẋ =(A 11
+ A 12 A −1
22 A 21)x. (4.32)
El resultado principal de esta sección es el Teorema 2 (abajo); previamente es conveniente definir
algunos términos. La matriz característica del sistema reducido (4.32) es
A 0 = A 11 + A 12 A −1
22 A 21. (4.33)
El espectro de la matriz A 0 (el conjunto de autovalores de A 0 ) se nota Λ = {λ 1 ,...,λ n }, donde
los autovalores repetidos aparecen tantas veces como sea su multiplicidad. El espectro de A 22 se
notará como Γ = {γ 1 ,...γ m }.
Si una matriz cuadrada tiene todos sus autovalores con parte real no nula se denomina hiperbólica;
se dice que es Hurwitz si todos tienen parte real negativa.
Teorema 2 Cotas sobre los autovalores. En el sistema lineal de perturbaciones singulares
(4.29) se supone que A 22 es no singular, y A 0 es la matriz definida por (4.33). Entonces, dado
δ > 0 existe un ε 0 > 0 tal que los m + n autovalores α 1 ,...,α m+n de la matriz
à !
A11 A 12
A ε =
(4.34)
A 21 /ε A 22 /ε
satisfacen las cotas
|α i − λ i | < δ, para i =1,...n, (4.35)
¯
¯εαi − γ i−n¯¯ < δ, para i = n +1,...n+ m. (4.36)
(donde los λ 1 ,...,λ n son los autovalores de A 0 , y γ 1 ,...,γ m son los autovalores de A 22 )para
cualquier 0 < |ε| < ε 0 . 4
Prueba. Para calcular los autovalores de A ε es conveniente aplicar una transformación de similaridad
T sobre A ε de modo que la matriz resultante T −1 A ε T resulte triangular a bloques. Una
tal matriz T está dada por
T =
Ã
In
!
M ε
0 m×n I m
con T −1 =
Ã
In
!
−M ε
.
0 m×n I m
Se debe buscar entonces una matriz M ε tal que
à !à !à ! à !
In −M ε A11 A 12 In M ε Fε 0 n×m
=
0 m×n I m A 21 /ε A 22 /ε 0 m×n I m G ε H ε
(4.37)

22
Expandiendo el triple producto matricial en el miembro izquierdo de (4.37) se encuentra que para
que el bloque 1,2 del producto sea cero la matriz M ε debe satisfacer
A 11 M ε + A 12 − 1 ε M εA 21 M ε − 1 ε M εA 22 = 0. (4.38)
Cuando ε → 0 algunos términos (4.38) tienden a infinito;paraevitaresteproblemasesuponeque
M ε tiene la forma
M ε = εP ε . (4.39)
Sustituyendo en (4.38) y simplificando, se encuentra que P ε debe verificar
εA 11 P ε + A 12 − εP ε A 21 P ε − P ε A 22 = 0. (4.40)
Esta ecuación está bien definida cuando ε → 0; en efecto, haciendo ε =0en (4.40) se obtiene
A 12 − P 0 A 22 = 0, (4.41)
que puede resolverse para P 0 por la hipótesis de no singularidad de A 22 . Se tiene entonces
P 0 = A 12 A −1
22 .
Si ε 6= 0, (4.40) es cuadrática en P ε . Sin embargo, como los coeficientes en (4.40) son continuos en
ε, se puede concluir que para ε suficientemente pequeño existe una solución P ε de (4.40) que es
próxima a P 0 , P ε = P 0 + O(ε), aunque no necesariamente es la única solución de (4.40). Se elige
alguna de estas soluciones P ε ysedefine M ε como en (4.39). Expandiendo (4.37) se obtiene
Ã
Fε
Como se ha visto más arriba,
!
0 n×m
=
G ε H ε
y entonces de (4.42), se encuentra que
Ã
A11 − 1 ε M εA 21
1
ε A 21
0 n×m
1
ε A 21M ε + 1 ε A 22
P ε = P 0 + O(ε) =P ε = A 12 A −1
22 + O(ε),
!
(4.42)
y
F ε = A 11 − 1 ε M εA 21 = A 11 − P ε A 21
= A 11 − A 12 A −1
22 A 21 + O(ε)
= A 0 + O(ε), (4.43)
H ε = 1 ε A 21M ε + 1 ε A 22 = 1 ε A 22 + A 21 P ε
= 1 ε A 22 + A 21 A 12 A −1
22
+ O(ε) (4.44)
Como la matriz en (4.42) es triangular en bloques, el espectro de A ε es la unión del espectro de
F ε con el espectro de H ε . Cuando ε → 0, es evidente de (4.43) que F ε → A 0 , yporlotantoel
espectro de F ε se aproxima al de A 0 , o, en otras palabras, se verifica la cota (4.35). Finalmente,
para ε → 0, el término A 22 /ε de (4.44) domina sobre los demás términos (A 22 es no singular) y
por lo tanto se satisface la cota (4.36). 2
Los autovalores de la matriz A ε son los modos naturales del sistema completo (4.29). Las desigualdades
(4.35)-(4.36) implican que, cuando ε → 0, nautovalores de A ε convergen a los autovalores
de A 0 , y los restantes m autovalores tienden a infinito, asintóticamente como γ i /ε. Este fenómeno
se observa en el Ejemplo 4.8 y la Fig. 4.6. Si λ i es un autovalor de A 0 con multiplicidad r i ,

4.5. PERTURBACIONES SINGULARES EN SISTEMAS LINEALES 23
exactamente r i autovalores de A ε convergen a λ i ; lo mismo ocurre con los autovalores γ i con
multiplicidad s i de A 22 .
Si todos los autovalores de A ε tienen parte real negativa, la solución del problema completo (4.29)
tienden a 0 cuando t →∞para cada condición inicial; se dice que el sistema (4.29) es asintóticamente
estable. Por otra parte, si alguno de los autovalores de A ε tiene parte real positiva, la
norma de las soluciones de (4.29) tienden a infinito cuando t →∞para casi todas las condiciones
iniciales; se dice entonces que el sistema es inestable.
El siguiente Teorema es un corolario del Teorema 2.
Teorema 3 Estabilidad de sistemas lineales de perturbaciones singulares
Dada la matriz A ε (4.34) característica del sistema completo (4.29) y suponiendo que la matriz
A 22 es no singular, las siguientes afirmaciones son equivalentes:
1. Existe un ε 0 > 0 tal que A ε es Hurwitz para 0 < ε < ε 0 .
2. Las matrices A 0 y A 22 son Hurwitz. 4
En el léxico de perturbaciones singulares la matriz A 22 representa la dinámica rápida, mientras
que la matriz A 0 representa la dinámica lenta. El razonamiento detrás de esta terminología puede
explicarse aproximadamente como sigue.
Si tanto A 0 como A 22 son Hurwitz, para cada ε suficientemente pequeño y positivo se define M ε
como la solución de (4.38) tal que M ε = εP ε → A 12 A −1
22 cuando ε → 0. Se define un nuevo vector
de estados
à ! à à !Ã
wε x I Mε x
= T =
(4.45)
z z!
0 I z!
donde la variable w ε = x − M ε z. La expresión (4.37) muestra que la dinámica del nuevo vector de
estado está gobernada por
! Ã !Ã !
Ãẇε Fε 0 n×m wε
=
ż G ε H ε z
o, en forma expandida,
ẇ ε = F ε w ε ,
(4.46)
ż = G ε w ε + H ε z.
De manera análoga al escalado temporal (4.13) efectuado en la Sección 4.3, se define la variable
temporal “rápida” τ =(t − t 0 )/ε, ysedefinen las funciones ¯z(τ), ¯w ε (τ) como
¯z(τ)= z(ετ + t 0 ), ¯w ε (τ)= w ε (ετ + t 0 ).
que son versiones escaladas en tiempo por un factor ε de z(·) y w(·). Se observa que
d¯z(τ)
= ε dz(t)
¯ .
dτ dt
¯t=ετ+t0
Con este cambio de la variable independiente, las ecuaciones de sistema (4.46) se pueden escribir
como
dw ε (t)
dt
= F ε w ε (4.47)
d¯z(τ)
dτ
= εH ε¯z(τ)+εG ε ¯w ε (τ). (4.48)
Estas ecuaciones permiten comprender mejor el comportamiento temporal de las funciones w ε (t)
y ¯z(τ). La ecuación (4.47) muestra que la respuesta temporal de w ε (t) es independiente de las
condición inicial z 0 = z(t 0 ) y depende solamente de la condición inicial w ε (t 0 ). Como M ε → 0

24
cuando ε → 0, se observa de (4.45) que w ε (t 0 ) tiende a x(t 0 ) cuando ε → 0. Por otra parte, (4.48)
muestra que ¯w ε (τ) actúa como una entrada al sistema cuya salida es ¯z(τ). Si w ε (t 0 )=0, para
todo t ≥ t 0 ,entonces su versión escalada ¯w ε (τ) ≡ 0 para todo τ ≥ 0, y (4.48) se simplifica a
d¯z(τ)
= εH ε¯z(τ).
dτ
De (4.44) se nota que εH ε → A 22 cuando ε → 0. Por lo tanto, a medida que ε → 0 la variable
¯z(τ) luce aproximadamente como
¯z(τ) =¯z(0)e A22τ .
Si w ε (t 0 ) 6= 0, entonces de (4.47),
w ε (t) =w ε (t 0 )e F ε(t−t 0 ) ∼ = wε (t 0 )e A 0(t−t 0 ) , (4.49)
pues F ε → A 0 cuando ε → 0. Entonces, si ε es muy pequeño, para estudiar el comportamiento de
(4.48) se puede considerar que ¯w ε (τ) como un vector constante ¯w ε (τ) =w ε (t 0 ) para todo τ ≥ 0
en la escala de tiempo del sistema rápido. Notando que según (4.42) εG ε = A 21 , la solución
aproximada de (4.48) es entonces 1
¯z(τ) ∼ = e
A 22 τ [¯z(0) + A −1
22 A 21 ¯w ε (0)] − A −1
22 A 21 ¯w ε (0)
∼= e A22t/ε [¯z(0) + A −1
22 w ε(t 0 )] − A −1
22 A 21w ε (t 0 ) (4.50)
La ecuación (4.50) muestra porqué la variable z se suele denominar variable de estado rápida,
y también que la dinámica “rápida” está determinada por la matriz A 22 . Como muestra (4.47)
cuando ε → 0 la matriz M ε → 0, y el vector w ε → x, lo que justifica la denominación de x como
variable de estado lenta, y su evolución temporal está regida por la matriz A 0 como muestra (4.49).
Ejemplo 4.14 Circuito eléctrico con diodo túnel
Para el sistema del Ejemplo 4.3, se tiene que x =(x 1,x 2) t , z =z,
⎛
− R ⎞
1 1
µ Ã !
A 11 = ⎜
L 1 L 1
⎝
− 1 − 1 ⎟
⎠ , A R2 − R 0 µ
d
22 =
, A 12 = 1 , A 21 = 0
R 2 R d
C 1 R 2 C
R
1
2C 1
y
A 0 = A 11 + A 12A −1
22 A 21 =
⎛
⎜
⎝
− 1 C 1
− R1
L 1
1
−
⎞
L 1
⎟
1
(R 2 − R d )C 1
⎠ .
1
R 2
Se puede verificar que A 0 es Hurwitz si R 2 >R d . Sin embargo, en estas condiciones la matriz de la dinámica
rápida A 22 > 0, i. e. A 22 no es Hurwitz. Aplicando el Teorema 3 se concluye que si 0

4.6. REFERENCIAS 25
4.6 Referencias
H. K. Khalil, Nonlinear Systems, 3ra ed., Prentice-Hall, Upper Saddle River, 2002.
R. Sepulchre, M. Janković, P. Kokotović, Constructive Nonlinear Control, Springer-Verlag, London,
1997, p. 154.
H. J. Sussmann, P. Kokotović, “The Peaking Phenomenon and the Global Stabilization of Nonlinear
Systems”, IEEE Trans. Aut. Control, 36, 4, August 1991, pp. 424-440.
M. Vidyasagar, Nonlinear System Analysis, Prentice-Hall, Englewood Cliffs, New Jersey, 1993.