Pruebas no paramÃ©tricas para comparar curvas de supervivencia ...

More documents

Recommendations

Info

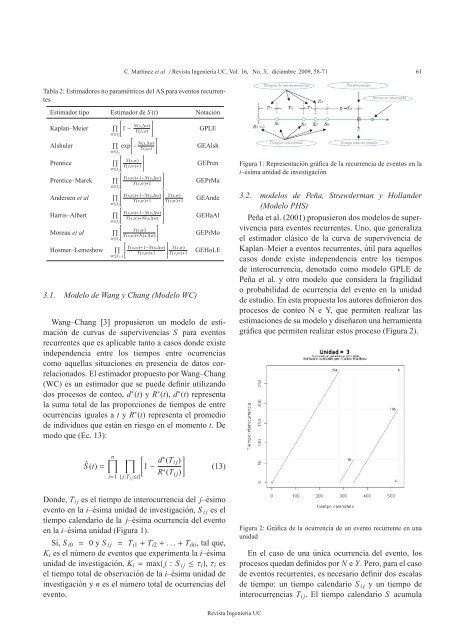
C. Martínez et al / Revista Ingeniería UC, Vol. 16, No. 3, diciembre 2009, 58-71 61Tabla 2: Estimadores no paramétricos del AS para eventos recurrentesEstimador tipo Estimador de S (t) Notación[ ]∏Kaplan–Meier1− N(s,∆w)Y(s,w)GPLEw≤t j[ ]∏Alshulerexp− N(s,∆w)Y(s,z)GEAlshw≤t j[ ]∏ Y(s,w)PrenticeY(s,w)+1GEPrenw≤t j[ ]∏ Y(s,w)+1−N(s,∆w)Prentice–MarekY(s,w)+1GEPrMaw≤t j[ ]∏ Y(s,w)+1−N(s,∆w) Y(s,w)Andersen et alY(s,w)+1 Y(s,w)+1GEAndew≤t j[ ]∏ Y(s,w)+1−N(s,∆w)Harris–AlbertY(s,w)+N(s,∆w)GEHaAlw≤t j[ ]∏ Y(s,w)Moreau et alY(s,w)+N(s,∆w)GEPrMow≤t j[ ]∏ Y(s,w)+1−N(s,∆w) Y(s,w)Hosmer–LemeshowY(s,w)+1 Y(s,w)+1GEHoLEw≤t j−13.1. Modelo de Wang y Chang (Modelo WC)Wang–Chang [3] propusieron un modelo de estimaciónde curvas de supervivencias S para eventosrecurrentes que es aplicable tanto a casos donde existeindependencia entre los tiempos entre ocurrenciascomo aquellas situaciones en presencia de datos correlacionados.El estimador propuesto por Wang–Chang(WC) es un estimador que se puede definir utilizandodos procesos de conteo, d ∗ (t) y R ∗ (t), d ∗ (t) representala suma total de las proporciones de tiempos de entreocurrencias iguales a t y R ∗ (t) representa el promediode individuos que están en riesgo en el momento t. Demodo que (Ec. 13):Figura 1: Representación gráfica de la recurrencia de eventos en lai–ésima unidad de investigación3.2. modelos de Peña, Strawderman y Hollander(Modelo PHS)Peña et al. (2001) propusieron dos modelos de supervivenciapara eventos recurrentes. Uno, que generalizael estimador clásico de la curva de supervivencia deKaplan–Meier a eventos recurrentes, útil para aquelloscasos donde existe independencia entre los tiemposde interocurrencia, denotado como modelo GPLE dePeña et al. y otro modelo que considera la fragilidado probabilidad de ocurrencia del evento en la unidadde estudio. En esta propuesta los autores definieron dosprocesos de conteo N e Y, que permiten realizar lasestimaciones de su modelo y diseñaron una herramientagráfica que permiten realizar estos proceso (Figura 2).Ŝ (t)=n∏∏i=1{ j:T i j ≤t}[1− d∗ (T i j )R ∗ (T i j )](13)Donde, T i j es el tiempo de interocurrencia del j–ésimoevento en la i–ésima unidad de investigación, S i j es eltiempo calendario de la j–ésima ocurrencia del eventoen la i–ésima unidad (Figura 1).Sí, S i0 = 0 y S i j = T i1 + T i2 +...+T iki , tal que,K i es el número de eventos que experimenta la i–ésimaunidad de investigación, K i = max{ j : S i j ≤τ i },τ i esel tiempo total de observación de la i–ésima unidad deinvestigación y n es el número total de ocurrencias delevento.Figura 2: Gráfica de la ocurrencia de un evento recurrente en unaunidadEn el caso de una única ocurrencia del evento, losprocesos quedan definidos por N e Y. Pero, para el casode eventos recurrentes, es necesario definir dos escalasde tiempo: un tiempo calendario S i j y un tiempo deinterocurrencias T i j . El tiempo calendario S acumulaRevista Ingeniería UC
62 C. Martínez et al / Revista Ingeniería UC, Vol. 16, No. 3, diciembre 2009, 58-71los tiempos de interocurrencias T en cada una de lasunidades bajo estudio. Los procesos N e Y se definencomo: N(s, t) e Y(s, t). Donde, N(s, t) representa elnúmero de eventos observados en el período calendario[0, s] con tiempos de interocurrencias menores e igualesa t e Y(s, t) representa el número el número deeventos observados en el período calendario [0, s] contiempos de interocurrencias mayores e iguales1 a t.De modo que, si N i (s, t) es el número de eventosobservados en el período calendario [0, s] con tiemposde interocurrencias menores e iguales a t para la i–ésima unidad de investigación, Y i (s, t) será el númerode eventos observados en el período calendario [0, s]con tiempos de interocurrencias mayores e iguales a t,en cada unidad bajo estudio (Ec. 14 a 16).N(s, t)=Y(s, t)=Y(s, t)=n∑N i (s, t)i=1on∑ ∑K ii=1j=1{ }I T i j ≤ t(14)n∑Y i (s, t) (15)i=1{ Kin∑i=1∑j=1{ } { }}I T i j ≥ t + I τ i − S iKi ≥ t(16)De esta manera, el estimador generalizado del límite–producto de Kaplan–Meier propuestos por Peña et al.(2001), quedo definido como (Ec. 17):∏[Ŝ (t)= 1− N(s,∆w) ]Y(s, w)w≤t(17)(18)El otro modelo propuesto por es el modelo de fragilidaddonde se asume que existe una variable aleatoria nomedible o variable latente que representa el grado deheterogeneidad entre las unidades de los grupos enestudio, la cual se asume independiente de la censura.El termino fragilidad se entiende como heterogeneidadindividual, debido a que existen unidades que tienenmayor probabilidad de experimentar el evento queotros. Este es conocido como modelo de fragilidadmultiplicativa y si se asume que la variable de fragilidadsigue una distribución gamma con parámetros de formay escala iguales a α. Si para cada unidad existeuna variable de fragilidad no observable y positiva,digamos Z i ; tal que, para cada momento t la función desupervivencia condicionada que definida en la Ec. 19:tS (t/Z i = z)=[S 0 (t)] z o S (t/Z i = z)=e −z ∫λ 0 (u)0 du(19)Donde,λ 0 (t) es la función de riesgo base y S 0 (t) esla función de supervivencia basal. Con, Z 1 , Z 2 ,...,Z ncomo las variables de fragilidad de las unidades,se asumen idénticamente distribuidas con una ciertadistribución común H para todas ellas. En el modeloFRMLE, H se distribuye gamma con parámetros deforma y escala iguales aα. La función S del modeloFRMLE se puede expresar como (Ec. 20):[ ] ααS (t)=(20)α+∧ 0 (t)Donde,∧ 0 (t) es la función de riesgo base acumulada.3.3. Otros modelos para análisis de supervivenciacon eventos recurrentesMartínez–Borges (2008) propusieron un conjuntode modelos no paramétricos del AS con eventosrecurrentes. Propuestas que se fundamentan en eltrabajo de Peña et al. (2001), quienes derivaron elestimador GPLE para eventos recurrentes, a partirde los estimadores clásicos Nelson–Aalen y Kaplan–Meier. Los autores del estimador GPLE diseñarondos procesos contadores a los que denotaron, con lasiguiente notación: N(s,t) y Y(s,t). La Tabla 2 ilustralos modelos propuestos por Martínez–Borges (2008).4. Pruebas clásicas del análisis de supervivencia4.1. IntroducciónEl objetivo de la comparación en el AS es similara aquellos procedimientos diseñados para compararestadísticos provenientes de muestras independientes,como la prueba t, la prueba de los signos, la pruebano paramétrica de los rangos signados de Wilcoxon(1945), la prueba U de Mann–Whitney (1947), laprueba de Kruskal–Wallis (1952), la prueba ponderadade Cochran (1954) y la prueba de análisis de varianzade dos o más vías. Todas estas pruebas de comparaciónse utilizan para evaluar diferencias entre estadísticosque han sido estimados basados en la información quese obtiene de subgrupos poblaciones independientesentre si. Sin embargo, en el AS sucede un fenómeno queno es considerado en estas pruebas que es la censura.Esta es la razón que imposibilita la aplicación directaRevista Ingeniería UC
Page 1 and 2: REVISTA INGENIERíA UC, VOL. 16, NO
Page 3: 60 C. Martínez et al / Revista Ing
Page 7 and 8: 64 C. Martínez et al / Revista Ing

Pruebas no paramÃ©tricas para comparar curvas de supervivencia ...

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?