Koko lehti - Matematiikkalehti Solmu - Helsinki.fi

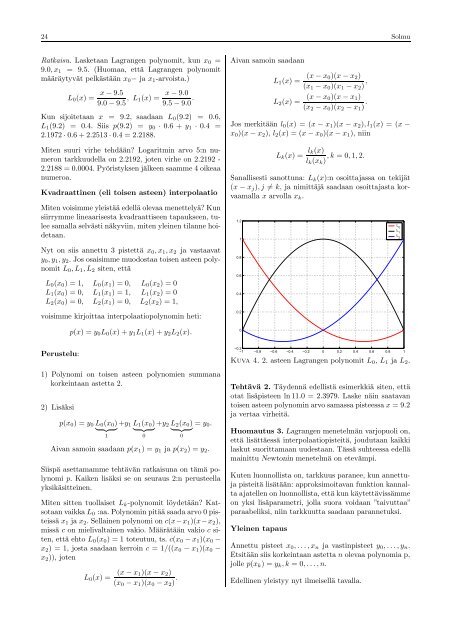
24 SolmuRatkaisu. Lasketaan Lagrangen polynomit, kun x 0 = Aivan samoin saadaanL 0 (x) = (x − x 1)(x − x 2 )(x 0 − x 1 )(x 0 − x 2 ) . Edellinen yleistyy nyt ilmeisellä tavalla.9.0, x 1 = 9.5. (Huomaa, että Lagrangen polynomitmääräytyvät pelkästään x 0 − ja x 1 -arvoista.)L 0 (x) = x − 9.59.0 − 9.5 , L 1(x) = x − 9.09.5 − 9.0 .L 1 (x) = (x − x 0)(x − x 2 )(x 1 − x 0 )(x 1 − x 2 ) ,L 2 (x) = (x − x 0)(x − x 1 )(x 2 − x 0 )(x 2 − x 1 ) .Kun sijoitetaan x = 9.2, saadaan L 0 (9.2) = 0.6,L 1 (9.2) = 0.4. Siis p(9.2) = y 0 · 0.6 + y 1 · 0.4 =2.1972 · 0.6 + 2.2513 · 0.4 = 2.2188.Miten suuri virhe tehdään? Logaritmin arvo 5:n numerontarkkuudella on 2.2192, joten virhe on 2.2192 -Jos merkitään l 0 (x) = (x − x 1 )(x − x 2 ), l 1 (x) = (x −x 0 )(x − x 2 ), l 2 (x) = (x − x 0 )(x − x 1 ), niinL k (x) = l k(x), k = 0, 1, 2.l k (x k )2.2188 = 0.0004. Pyöristyksen jälkeen saamme 4 oikeaanumeroa.Kvadraattinen (eli toisen asteen) interpolaatioSanallisesti sanottuna: L k (x):n osoittajassa on tekijät(x − x j ), j ≠ k, ja nimittäjä saadaan osoittajasta korvaamallax arvolla x k .Miten voisimme yleistää edellä olevaa menettelyä? Kunsiirrymme lineaarisesta kvadraattiseen tapaukseen, tuleesamalla selvästi näkyviin, miten yleinen tilanne hoi-1.2L 0L 1detaan.L 21Nyt on siis annettu 3 pistettä x 0 , x 1 , x 2 ja vastaavaty 0 , y 1 , y 2 . Jos osaisimme muodostaa toisen asteen polynomit0.8L 0 , L 1 , L 2 siten, että0.6L 0 (x 0 ) = 1, L 0 (x 1 ) = 0, L 0 (x 2 ) = 0L 1 (x 0 ) = 0, L 1 (x 1 ) = 1, L 1 (x 2 ) = 00.4L 2 (x 0 ) = 0, L 2 (x 1 ) = 0, L 2 (x 2 ) = 1,0.2voisimme kirjoittaa interpolaatiopolynomin heti:p(x) = y 0 L 0 (x) + y 1 L 1 (x) + y 2 L 2 (x).Perustelu:0−0.2−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1Kuva 4. 2. asteen Lagrangen polynomit L 0 , L 1 ja L 2 .1) Polynomi on toisen asteen polynomien summanakorkeintaan astetta 2.Tehtävä 2. Täydennä edellistä esimerkkiä siten, ettäotat lisäpisteen ln 11.0 = 2.3979. Laske näin saatavan2) Lisäksitoisen asteen polynomin arvo samassa pisteessa x = 9.2ja vertaa virheitä.p(x 0 ) = y 0 L 0 (x 0 ) +y 1 L 1 (x 0 ) +y 2 L 2 (x 0 ) = y 0 .} {{ } } {{ } } {{ } Huomautus 3. Lagrangen menetelmän varjopuoli on,100että lisättäessä interpolaatiopisteitä, joudutaan kaikkiAivan samoin saadaan p(x 1 ) = y 1 ja p(x 2 ) = y 2 . laskut suorittamaan uudestaan. Tässä suhteessa edellämainittu Newtonin menetelmä on etevämpi.Siispä asettamamme tehtävän ratkaisuna on tämä polynomip. Kaiken lisäksi se on seuraus 2:n perusteellaKuten luonnollista on, tarkkuus paranee, kun annettujapisteitä lisätään: approksimoitavan funktion kannal-yksikäsitteinen.ta ajatellen on luonnollista, että kun käytettävissämmeMiten sitten tuollaiset L k -polynomit löydetään? Katsotaanvaikka L 0 :aa. Polynomin pitää saada arvo 0 pisteissäon yksi lisäparametri, jolla suora voidaan ”taivuttaa”paraabeliksi, niin tarkkuutta saadaan parannetuksi.x 1 ja x 2 . Sellainen polynomi on c(x−x 1 )(x−x 2 ),missä c on mielivaltainen vakio. Määrätään vakio c siten,Yleinen tapausettä ehto L 0 (x 0 ) = 1 toteutuu, ts. c(x 0 − x 1 )(x 0 −x 2 ) = 1, josta saadaan kerroin c = 1/((x 0 − x 1 )(x 0 − Annettu pisteet x 0 , . . . , x n ja vastinpisteet y 0 , . . . , y n .x 2 )), jotenEtsitään siis korkeintaan astetta n olevaa polynomia p,jolle p(x k ) = y k , k = 0, . . . , n.