Linee di trasmissione ordinarie - circuito equivalente e parametri ...
Linee di trasmissione ordinarie - circuito equivalente e parametri ...
Linee di trasmissione ordinarie - circuito equivalente e parametri ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>Linee</strong> <strong>di</strong> TX or<strong>di</strong>narie – rappresentazione circuitale (1/2)<br />
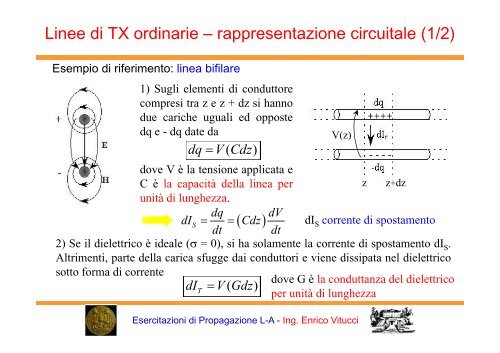
Esempio <strong>di</strong> riferimento: linea bifilare<br />
1) Sugli elementi <strong>di</strong> conduttore<br />
compresitrazez+dzsihanno<br />
due cariche uguali ed opposte<br />
dq e-dq date da<br />
dq = V ( Cdz)<br />
V(z)<br />
dove V è la tensione applicata e<br />
Cèla capacità della linea per<br />
unità <strong>di</strong> lunghezza.<br />
z z+dz<br />
dq<br />
dV<br />
dI S<br />
( Cdz<br />
)<br />
dt<br />
dt<br />
dI corrente <strong>di</strong> spostamento<br />
S<br />
2) Se il <strong>di</strong>elettrico è ideale (σ = 0), si ha solamente la corrente <strong>di</strong> spostamento dI S .<br />
Altrimenti, parte della carica sfugge dai conduttori e viene <strong>di</strong>ssipata nel <strong>di</strong>elettrico<br />
sotto forma <strong>di</strong> corrente<br />
dove G è la conduttanza del <strong>di</strong>elettrico<br />
dIT<br />
= V ( Gdz)<br />
per unità <strong>di</strong> lunghezza<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
<strong>Linee</strong> <strong>di</strong> TX or<strong>di</strong>narie – rappresentazione circuitale (2/2)<br />
3) Inoltre la superficie ABCD in<strong>di</strong>cata in figura è attraversata da un flusso <strong>di</strong><br />
induzione magnetica (flusso concatenato con la linea ABCD):<br />
( )<br />
dΦ=<br />
I Ldz<br />
dove I è la corrente che fluisce nella “spira”<br />
ABCD ed L rappresenta la induttanza per<br />
unità <strong>di</strong> lunghezza.<br />
V(z)<br />
V(z+dz)<br />
dV<br />
i<br />
dI<br />
Ldz dt<br />
( )<br />
= dV i tensione auto-indotta<br />
σ = ∞<br />
4) Se i conduttori sono ideali ( ), si ha solamente la tensione auto-indotta dV i .<br />
Altrimenti, la tensione cala ulteriormente lungo la <strong>di</strong>rezione z, a causa della<br />
resistenza it non nulla <strong>di</strong> dei conduttori:<br />
dove R è la resistenza dei conduttori<br />
dVC<br />
= V ( z + dz) − V ( z) = ( Rdz)<br />
I<br />
per unità <strong>di</strong> lunghezza<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
<strong>Linee</strong> <strong>di</strong> TX or<strong>di</strong>narie – <strong>circuito</strong> <strong>equivalente</strong><br />
I(z)<br />
R dz<br />
L dz<br />
I(z+dz)<br />
V(z)<br />
G dz<br />
C dz<br />
V(z+dz)<br />
z<br />
z+dz<br />
In generale, V e I funzione della coor<strong>di</strong>nata assiale (z) e del tempo!<br />
L, C, G, R <strong>parametri</strong> primari della linea (per unità <strong>di</strong> lunghezza)<br />
Modello a <strong>parametri</strong> <strong>di</strong>stribuiti<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Parametri concentrati vs <strong>parametri</strong> <strong>di</strong>stribuiti (1/2)<br />
• In linea teorica, è possibile anche una descrizione a <strong>parametri</strong> concentrati<br />
delle linee <strong>di</strong> <strong>trasmissione</strong>: basta schematizzare la linea come una<br />
cascata <strong>di</strong> quadripoli, a patto <strong>di</strong> <strong>di</strong>mensionare la lunghezza <strong>di</strong> ciascun<br />
quadripolo in modo che sia rispettata la con<strong>di</strong>zione <strong>di</strong> quasi-stazionarietà.<br />
Δ Δ Δ<br />
• Talemodelloèperòvalidosoloin una banda <strong>di</strong> frequenza superiormente<br />
limitata [0 , f MAX<br />
].<br />
v p<br />
• Infatti, deve essere sod<strong>di</strong>sfatta la con<strong>di</strong>zione Δλ min<br />
, con<br />
λ<br />
min<br />
=<br />
f max<br />
• La con<strong>di</strong>zione <strong>di</strong> quasi-stazionarietà si può ritenere in pratica sod<strong>di</strong>sfatta<br />
se risulta KΔ < λ min con K abbastanza grande.<br />
• Ad esempio, se si assume K=10 deve essere:<br />
Δ <<br />
1<br />
min<br />
10 λ Δ<br />
max<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Parametri concentrati vs <strong>parametri</strong> <strong>di</strong>stribuiti (2/2)<br />
• Nota la massima frequenza <strong>di</strong> lavoro ammissibile, è imme<strong>di</strong>ato ricavare il<br />
parametro Δ , e da esso il numero minimo <strong>di</strong> quadripoli in cascata con<br />
max<br />
cui è necessario schematizzare la linea affinché il modello a <strong>parametri</strong><br />
concentrati sia valido:<br />
n<br />
⎡ <br />
⎤<br />
= int ⎢ ⎥<br />
⎣Δ<br />
max ⎦<br />
essendo int[ ] il numero intero imme<strong>di</strong>atamente<br />
superiore alla quantità entro le parentesi<br />
• Si noti che questo è in ogni caso un modello approssimato, mentre il<br />
modello a <strong>parametri</strong> <strong>di</strong>stribuiti è un modello rigoroso (si può ricavare<br />
<strong>di</strong>rettamente dalle eq. <strong>di</strong> Maxwell, senza fare approssimazioni).<br />
• Inoltre, il modello a <strong>parametri</strong> <strong>di</strong>stribuiti non ha limitazioni in frequenza.<br />
Infatti, esso si può immaginare come il limite del modello a <strong>parametri</strong><br />
concentrati ti quando la lunghezza dei quadripoli <strong>di</strong> <strong>di</strong>venta infinitesima.<br />
it i<br />
Essendo Δ =dz , la con<strong>di</strong>zione <strong>di</strong> quasi-stazionarietà risulta sod<strong>di</strong>sfatta<br />
anche per , cioè per f →∞.<br />
λ → max<br />
min<br />
0<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
<strong>Linee</strong> <strong>di</strong> TX in regime sinusoidale<br />
Si consideri ora una linea alimentata con una tensione sinusoidale ad una<br />
frequenza f=ω/2π. In regime sinusoidale, tensioni e correnti vengono<br />
sostituite dalle rispettive grandezze complesse rappresentative ti (fasori).<br />
Si è visto che me<strong>di</strong>ante il modello a <strong>parametri</strong> <strong>di</strong>stribuiti si può<br />
schematizzare la linea come una cascata <strong>di</strong> quadripoli <strong>di</strong> lunghezza<br />
infinitesima:<br />
it i<br />
Z dz Z dz Z dz Z dz<br />
Y dz Y dz Y dz Y dz<br />
Si ha quin<strong>di</strong>:<br />
• V=V(z) e I=I(z)<br />
• Z = R +jωL<br />
• Y=G+jωC<br />
Fasori funzione solo <strong>di</strong> z<br />
Impedenza serie (per unità <strong>di</strong> lunghezza)<br />
Ammettenza parallelo (per unità <strong>di</strong> lunghezza)<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Equazioni dei telefonisti<br />
Dal <strong>circuito</strong> <strong>equivalente</strong> in regime sinusoidale si deduce:<br />
I(z)<br />
( +<br />
) ( ) ( ) ( )<br />
( ) ( ) ( ) ( )<br />
⎧⎪<br />
dV = V z + dz − V z =−<br />
Zdz I z<br />
⎨<br />
⎪⎩ dI = I z + dz − I z =− Ydz V z<br />
V(z) Ydz<br />
Zdz<br />
I(z+dz)<br />
V(z+dz)<br />
e <strong>di</strong>videndo per dz:<br />
⎧<br />
dV<br />
= −ZI<br />
⎪ dz<br />
⎪<br />
dI<br />
= −YV<br />
⎪⎩ dz<br />
Equazioni dei telefonisti<br />
⎨<br />
⎪<br />
f ’<br />
Le equazioni dei telefonisti sono l’<strong>equivalente</strong> circuitale delle equazioni<br />
<strong>di</strong> Maxwell, per le linee <strong>di</strong> TX. Ai fini della trattazione svolta per le linee,<br />
esse sostituiscono completamente le eq. <strong>di</strong> Maxwell.<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Equazioni dei telefonisti: risoluzione (1/2)<br />
Per risolvere le equazioni dei telefonisti occorre <strong>di</strong>saccoppiarle. A tal fine<br />
si derivi la prima rispetto a z:<br />
d 2 V<br />
dz 2<br />
= - Z dI<br />
dz<br />
Ricavando dI/dz dalla seconda e sostituendolo nella equazione<br />
precedente si ottiene:<br />
d 2 V<br />
2 - ZY V = 0 Equazione dei telegrafisti<br />
dz<br />
L’integrale generale <strong>di</strong> questa equazione è del tipo:<br />
+<br />
V() z = V 0 e<br />
- ZY z +<br />
- V0 e<br />
ZY z<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Equazioni dei telefonisti: risoluzione (2/2)<br />
Derivando la precedente soluzione e sostituendola nella seconda<br />
equazione dei telefonisti, si ottiene la soluzione in termini <strong>di</strong> correnti:<br />
I(z) = - 1 dV(z) Y<br />
=<br />
V + - ZY z Y<br />
0 e -<br />
Z dz Z Z<br />
V 0<br />
- e<br />
ZY z<br />
Si osservi che tutte le quantità presenti in tali soluzioni sono complesse.<br />
I due termini presenti nelle soluzioni hanno il significato <strong>di</strong> onde <strong>di</strong><br />
tensione e <strong>di</strong> corrente che si propagano in <strong>di</strong>rezione assiale,<br />
rispettivamente nella <strong>di</strong>rezione delle z positive e delle z negative. Tali<br />
onde hanno una costante <strong>di</strong> propagazione (assiale):<br />
Γ = α + jβ = ZY =<br />
( R + jω L) ⋅ ( G + jω C) ; α,β ∈ R<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
<strong>Linee</strong> <strong>di</strong> TX: <strong>parametri</strong> secondari (1/2)<br />
Elevando al quadrato ambo i membri e uguagliando parti reali e<br />
immaginarie si ottiene:<br />
⎧ α 2 - β 2 = RG - ω 2 LC<br />
⎨<br />
⎩ 2αβ = ω( CR + LG)<br />
einfinesiricavanoleespressioni<strong>di</strong>α e β in funzione dei <strong>parametri</strong><br />
primari i della linea:<br />
α =<br />
β =<br />
1<br />
( R 2 + ω 2 L 2<br />
)( G 2 + ω 2 C 2<br />
) - ( ω 2 LC - RG<br />
)<br />
2<br />
1<br />
2<br />
( R 2 + ω 2 L 2 )( G 2 + ω 2 C 2 ) + ( ω 2 LC - RG)<br />
α costante <strong>di</strong> attenuazione; β costante <strong>di</strong> fase<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
<strong>Linee</strong> <strong>di</strong> TX: <strong>parametri</strong> secondari (2/2)<br />
Si definisce inoltre la grandezza:<br />
Z c<br />
=<br />
Z<br />
Y<br />
=<br />
R +<br />
G +<br />
jωL<br />
j ω C<br />
Impedenza caratteristica della linea<br />
α, β e Zc sono detti <strong>parametri</strong> secondari della linea (<strong>di</strong>pendono dai<br />
<strong>parametri</strong> primari C, L, G, R).<br />
Le soluzioni delle eq. dei telefonisti si possono quin<strong>di</strong> riscrivere così:<br />
+ Γ Γ +<br />
⎧<br />
+ -Γz - Γz + - V (z ) = V0 e + V0 e = V (z ) + V (z )<br />
⎪<br />
⎨<br />
= V +<br />
0<br />
-Γz -<br />
V ⎪ I(z) e - 0 e Γz = I + (z ) - I - (z )<br />
⎩<br />
Z c<br />
Z c<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Onda progressiva e regressiva (1/4)<br />
V + (z), I + (z)<br />
V - (z), I - (z)<br />
Onda progressiva<br />
Onda regressiva<br />
Nel dominio dei tempi V + ha la forma:<br />
V<br />
V<br />
+<br />
+<br />
0<br />
( z<br />
, t<br />
)<br />
Re<br />
= Re V<br />
{<br />
+ - Γz<br />
jω<br />
t<br />
e e<br />
}<br />
0<br />
{ e e }<br />
-α<br />
z j( ω t - β z + ∠ V )<br />
+ -α<br />
z<br />
= V<br />
0<br />
e cos(<br />
ω t −<br />
β z +<br />
∠<br />
V<br />
0<br />
+<br />
0<br />
=<br />
=<br />
)<br />
V +<br />
t 0<br />
t 0 + Δt<br />
α +<br />
λ/2<br />
2<br />
z<br />
Si tratta <strong>di</strong> una sinusoide che si propaga<br />
nella <strong>di</strong>rezionei positiva ii dell'asse z<br />
attenuandosi esponenzialmente in ragione<br />
del termine e -αz .<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Onda progressiva e regressiva (2/4)<br />
La costante <strong>di</strong> fase β è legata alla velocità <strong>di</strong> propagazione dell’onda nel<br />
mezzo trasmissivo.<br />
ω t ± βz<br />
Equazione dei fronti d’onda:<br />
Differenziando:<br />
Velocità <strong>di</strong> propagazione dei fronti d’onda: d<br />
v<br />
p<br />
ω dt ± β dz<br />
= cost<br />
= 0<br />
dz ω<br />
= = = λ<br />
f Velocità <strong>di</strong> fase<br />
dt<br />
β<br />
v p è per definizione una grandezza positiva, e quin<strong>di</strong> assume il medesimo<br />
valore anche per la componente regressiva.<br />
La costante <strong>di</strong> attenuazione α è invece dovuta alle per<strong>di</strong>te, cioè alle non<br />
idealità <strong>di</strong> <strong>di</strong>elettrico e conduttori: infatti se nella espressione <strong>di</strong> α si pone<br />
R = G = 0 si ottiene α =0.<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Onda progressiva e regressiva (3/4)<br />
Lungo un tronco <strong>di</strong> linea <strong>di</strong> lunghezza l’onda progressiva subisce uno<br />
sfasamento temporale in ritardo (e la regressiva in anticipo) pari a:<br />
τ = <br />
v p<br />
essendo v p la velocità <strong>di</strong> fase dell’onda. τ prende il nome <strong>di</strong> tempo <strong>di</strong><br />
transito (o <strong>di</strong> ritardo <strong>di</strong> fase) del tronco <strong>di</strong> linea considerato. Lo<br />
sfasamento angolare nelle stesse con<strong>di</strong>zioni è invece:<br />
<br />
β = 2π = ωτ<br />
λ<br />
β <br />
prende anche il nome <strong>di</strong> lunghezza elettrica del tronco <strong>di</strong> linea (<br />
la lunghezza geometrica)<br />
<br />
è<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Onda progressiva e regressiva (4/4)<br />
• La generica soluzione in termini <strong>di</strong> tensione e corrente è quin<strong>di</strong> costituita<br />
dalla combinazione (o sovrapposizione), secondo opportuni coefficienti, <strong>di</strong><br />
un'onda progressiva e <strong>di</strong> un'onda regressiva.<br />
• L’onda regressiva nasce per effetto <strong>di</strong> una <strong>di</strong>somogeneità nella struttura:<br />
tipicamente, la linea viene terminata e chiusa su <strong>di</strong> un monoporta (carico),<br />
il quale “riflette in<strong>di</strong>etro” parte della potenza che incide su <strong>di</strong> esso.<br />
• Le ampiezze delle onde <strong>di</strong> tensione e <strong>di</strong> corrente sono legate tra loro<br />
tramite Z C , similmente a quanto avviene nel caso a costanti concentrate.<br />
• Le costanti V 0+ eV 0- definiscono il regime elettrico che si instaura all’interno<br />
della linea. Il loro valore è determinato una volta che siano note le<br />
con<strong>di</strong>zioni <strong>di</strong> alimentazione e <strong>di</strong> carico della linea.<br />
• Se |V 0- |>0, la sovrapposizione delle componenti progressiva e regressiva<br />
da’ origine ad un’onda stazionaria.<br />
• Se V 0- =0 Regime d’onda puramente progressiva<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Carico<br />
Nella pratica, una linea non si estende mai indefinitamente da z = - ∞ a<br />
z=+∞.<br />
La linea verrà cioè interrotta in una certa sezione, detta sezione <strong>di</strong> carico<br />
in cui verrà connessa ad un monoporta <strong>di</strong> impedenza Z L , che costituisce<br />
appunto il carico.<br />
I(z) ()<br />
. . . V(z)<br />
Z L<br />
z z = 0<br />
Per como<strong>di</strong>tà l'origine del sistema <strong>di</strong> riferimento verrà posto al carico, per<br />
cui tutte le sezioni della linea corrisponderanno a z negative.<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Impedenza e coefficiente <strong>di</strong> riflessione (1/3)<br />
Ci si ponga nella generica sezione <strong>di</strong> ascissa z. Si definisce coefficiente<br />
<strong>di</strong> riflessione ρ(z) alla ascissa z il rapporto:<br />
ρ(z) = V- z<br />
V + z<br />
()<br />
() = V<br />
-<br />
0<br />
e<br />
Γz<br />
V 0<br />
+ e<br />
-Γz<br />
Si definisce inoltre impedenza Zi(z) in una generica sezione il rapporto<br />
Z i (z) = V(z)<br />
I(z)<br />
che rappresenta l'impedenza del monoporta che si vede “guardando a<br />
destra” della sezione considerata (verso il carico).<br />
Al carico (z=0) si ha<br />
ρ L = ρ(0) = V 0 -<br />
⇒ ρ(z) = ρ L e 2Γz<br />
V 0<br />
+<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Impedenza e coefficiente <strong>di</strong> riflessione (2/3)<br />
Sulla sezione <strong>di</strong> carico (z=0) l’impedenza risulta:<br />
V + + V -<br />
Z L = Z i (0) = Z C V 0 + V 0<br />
V 0<br />
+ - V0<br />
-<br />
Confrontando le espressioni <strong>di</strong> ρ L e<strong>di</strong>Z L si può ricavare facilmente il<br />
legame fra le 2 grandezze:<br />
Z L = Z 1 + ρ L C oppure ρ<br />
1 - ρ L = Z L - Z C<br />
L Z L + Z C<br />
In modo analogo, si ricava il legame fra impedenza e coefficiente <strong>di</strong><br />
riflessione sulla generica sezione z:<br />
( ) Z i (z) = Z 1 + ρ(z)<br />
C e ρ(z) = Z i (z) - Z C<br />
1 - ρ(z)<br />
Z i (z) + Z C<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Impedenza e coefficiente <strong>di</strong> riflessione (3/3)<br />
Dalla prima delle 2 equazioni precedenti, ricordando che vale la relazione<br />
2 z<br />
ρ = ρ e Γ e sostituendo l’espressione <strong>di</strong> ρ L in funzione <strong>di</strong> Z c e Z L , si<br />
L<br />
ricava facilmente che:<br />
Z i (z) = Z Z L cosh(Γz) - Z C senh(Γz)<br />
C Z C cosh(Γz) - Z L senh(Γz)<br />
Tale relazione è estremamente utile perché permette <strong>di</strong> esprimere Z i (z),<br />
cioè il rapporto tra tensione e corrente nella generica sezione me<strong>di</strong>ante i<br />
<strong>parametri</strong> caratteristici della linea (Z C e Γ) e del carico (Z L ).<br />
Infine, le soluzioni i delle eq. dei telegrafisti ti si possono esprimere in funzione <strong>di</strong> ρ L :<br />
+<br />
( ) (<br />
−Γz<br />
Γz)<br />
0 ρL<br />
⎧ V z = V e + e<br />
⎪<br />
⎨ +<br />
V<br />
⎪<br />
−Γ<br />
I z = e −ρLe<br />
⎪⎩ ZC<br />
0<br />
( ) (<br />
z Γz)<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Regime elettrico <strong>di</strong> una linea <strong>di</strong> TX (1/2)<br />
La conoscenza del carico Z L consente <strong>di</strong> determinare facilmente ρ L ,cioè<br />
il rapporto V 0- /V 0+ .<br />
Per determinare esattamente V<br />
-<br />
0 e V 0+ , occorre conoscere, oltre al<br />
carico, le con<strong>di</strong>zioni <strong>di</strong> alimentazione della linea.<br />
In generale, una linea <strong>di</strong> lunghezza finita sarà alimentata nella sezione<br />
z =− me<strong>di</strong>ante una rete attiva, cioè un opportuno generatore.<br />
<br />
G<br />
(V G , Z G )<br />
Z L<br />
z = − z =<br />
0<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Regime elettrico <strong>di</strong> una linea <strong>di</strong> TX (2/2)<br />
Supponendo <strong>di</strong> poter schematizzare tale generatore me<strong>di</strong>ante un<br />
generatore ideale <strong>di</strong> tensione V G connesso in serie ad una impedenza Z G<br />
(impedenza interna del generatore), si avrà che:<br />
Associando tale equazione alla:<br />
V( − ) + Z I( − )<br />
= V<br />
G<br />
G<br />
V ( − ) = Z ( − ) I ( − ) = Z I<br />
( −<br />
<br />
)<br />
i<br />
si ottiene un sistema che può agevolmente essere risolto nelle incognite V ( −)<br />
e<br />
I<br />
( −<br />
)<br />
(si ricor<strong>di</strong> che V G e Z G sono termini noti, mentre Z IN può essere ricavata<br />
facilmente a partire dall’impedenza <strong>di</strong> carico Z L , anch’essa nota).<br />
NoteV ( − ) e I( −)<br />
, si determinano facilmente le costanti V 0+ eV 0- e quin<strong>di</strong><br />
le tensioni e le correnti in ogni sezione della linea, cioè si determina il<br />
regime elettrico della linea.<br />
IN<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Adattamento in uniformità (1/3)<br />
Un caso <strong>di</strong> notevole interesse pratico è quello in cui non è presente l'onda<br />
riflessa: regime d'onda puramente progressiva.<br />
Perché tale con<strong>di</strong>zione sia verificata deve risultare:<br />
Ricordando che<br />
ρ<br />
−<br />
( z<br />
)<br />
0<br />
ρL<br />
= 0 ∀z ⇒ V = 0 ⇒ = 0<br />
ρ<br />
L<br />
=<br />
Z<br />
Z<br />
L<br />
L<br />
− Z<br />
+ Z<br />
C<br />
C<br />
Z L<br />
= Z C<br />
(con<strong>di</strong>zione <strong>di</strong> adattamento in uniformità)<br />
La con<strong>di</strong>zione <strong>di</strong> adattamento corrisponde cioè ad una proprietà della<br />
linea e del carico: quando essi sono tali che Z L = Z C la con<strong>di</strong>zione <strong>di</strong><br />
adattamento è verificata ed il carico non "riflette" parte dell’ onda incidente<br />
all'in<strong>di</strong>etro, bensì la assorbe completamente.<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Adattamento in uniformità (2/3)<br />
Ricordando che<br />
ρ<br />
( z)<br />
si ricava anche che in adattamento<br />
=<br />
i<br />
( )<br />
( )<br />
Z z − Z<br />
Z z +<br />
Z<br />
i<br />
C<br />
C<br />
( ) ≡ = ∀z<br />
Z z Z Z<br />
i C L<br />
cioè in ogni sezione si "vede" sempre la stessa impedenza che coincide<br />
con la impedenza <strong>di</strong> carico e con la impedenza caratteristica della linea.<br />
In con<strong>di</strong>zioni <strong>di</strong> adattamento le soluzioni delle equazioni dei telefonisti<br />
<strong>di</strong>ventano<br />
+<br />
+ -Γz Γ + V (z) = V 0 e = V (z) I(z) = V 0<br />
e -Γz = I + (z)<br />
Z C<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Adattamento in uniformità (3/3)<br />
da cui si ricava imme<strong>di</strong>atamente:<br />
V(z) ( ) =Z C ⋅ I(z)<br />
Quando una linea <strong>di</strong> <strong>trasmissione</strong> è adattata, cioè è in regime <strong>di</strong> onda<br />
puramente progressiva, V ed I sono proporzionali secondo uncoefficiente<br />
i complesso che non <strong>di</strong>pende dalla sezione e coincide con l'impedenza<br />
caratteristica della linea. In regime d'onda puramente progressiva, vale<br />
quin<strong>di</strong> in ogni sezione una relazione analoga alla legge <strong>di</strong> Ohm.<br />
Questo risultato si poteva ricavare anche <strong>di</strong>rettamente dalla relazione<br />
Z i (z) = V(z)<br />
I(z)<br />
( )<br />
Z z ≡ Z<br />
ricordando che in adattamento risulta .<br />
i<br />
C<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Potenza complessa (1/5)<br />
La potenza complessa in generica sezione della linea è:<br />
1 * P C (z) = V(z) I (z) = P + jQ<br />
2<br />
dove I*(z) in<strong>di</strong>ca il complesso coniugato <strong>di</strong> I(z); inoltre<br />
P = Re{ P C }<br />
èlapotenza attiva che attraversa la generica sezione nel verso positivo<br />
all'asse z. Analogamente<br />
{ }<br />
Q = Im P C<br />
è la potenza reattiva.<br />
Esprimendo l’impedenza Z i (z) nel seguente modo:<br />
Z i ( z) = R i ( z) + j X i ( z)<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Potenza complessa (2/5)<br />
si ha:<br />
⎧<br />
P = Re⎨<br />
1 2 Z i I I * ⎫<br />
⎬<br />
⎩ ⎭ = 1 2 R i I 2<br />
⎧<br />
Q = Im ⎨<br />
1 2 Z i I I * ⎫<br />
⎬<br />
⎩ ⎭ = 1 2 X i I 2<br />
Si può <strong>di</strong>mostrare che la con<strong>di</strong>zione per avere il trasferimento della<br />
massima potenza al carico è la con<strong>di</strong>zione <strong>di</strong> adattamento in potenza<br />
Z *<br />
L = Z C<br />
Nel caso <strong>di</strong> linea priva <strong>di</strong> per<strong>di</strong>te (R = G = 0) la con<strong>di</strong>zione <strong>di</strong> adattamento<br />
in potenza coincide con quella <strong>di</strong> adattamento in uniformità, dovendo<br />
essere:<br />
*<br />
R L =R C = RC C<br />
In applicazioni <strong>di</strong> telecomunicazioni è molto più importante l'adattamento<br />
in uniformità perchè non si vuole trasferire potenza bensì informazione.<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Potenza complessa (3/5)<br />
Si consideri ora una linea adattata (in uniformità). Le onde <strong>di</strong> tensione e <strong>di</strong><br />
corrente assumono la forma:<br />
⎧ + −Γ z + − ( α<br />
+ jββ<br />
) z<br />
V ( z)<br />
= V0 e = V0<br />
e<br />
⎪<br />
⎨ + +<br />
V0 −Γz<br />
V0<br />
( α jβ)<br />
z<br />
− +<br />
⎪ ( ) = =<br />
⎪⎩<br />
I z Z<br />
e C Z<br />
e<br />
C<br />
La potenza complessa che attraversa una generica sezione della linea è:<br />
2<br />
1 1<br />
V<br />
+<br />
∗<br />
0<br />
−2α<br />
z<br />
−2α<br />
z<br />
Pc<br />
( z) = V ( z) I ( z) = e = Pc<br />
( z = 0)<br />
⋅e<br />
2 2 Z c<br />
Quin<strong>di</strong>, un’onda elettromagnetica che si propaga lungo una linea <strong>di</strong> <strong>trasmissione</strong><br />
<strong>di</strong> lunghezza<br />
<br />
subisce, per effetto delle per<strong>di</strong>te nei conduttori e nel <strong>di</strong>elettrico,<br />
un’attenuazione in potenza pari a:<br />
A<br />
( 0<br />
)<br />
( )<br />
Pc<br />
= =<br />
P<br />
c<br />
e<br />
2α<br />
<br />
Esprimendo l’attenuazione in dB si ha:<br />
( ) 10log 2α<br />
<br />
10log 2 α<br />
( / )<br />
AdB = e = ⋅ e adB m⋅<br />
10 10<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
( )<br />
Potenza complessa (4/5)<br />
a dB/<br />
m èl’attenuazione specifica, cioèl’attenuazione che il segnale subisce<br />
lungo un tronco <strong>di</strong> linea <strong>di</strong> lunghezza 1 m, espressa in dB:<br />
( )<br />
⎡ Pc<br />
z = 0<br />
⎤<br />
2α<br />
a( dB/ m)<br />
= 10log10 ⎢ ⎥ = 10log10 e = α ⋅20log10<br />
e<br />
8.686⋅α<br />
⎢⎣Pc<br />
( z = 1 m)<br />
⎥⎦<br />
Nei collegamenti su portante fisico, vale una formula <strong>di</strong> <strong>trasmissione</strong> analoga<br />
all’equazione <strong>di</strong> Friis per i collegamenti ra<strong>di</strong>o in spazio libero. Si ha:<br />
P TX<br />
A<br />
G<br />
P RX<br />
RX<br />
( ) = ( ) + ( ) − ( )<br />
P dBW P dBW G dB A dB<br />
TX<br />
dove G rappresenta il guadagno g <strong>di</strong> tratta, cioèlasommadeiguadagni g <strong>di</strong> potenza<br />
degli amplificatori, mentre A è l’attenuazione in potenza che il segnale subisce per<br />
effetto delle per<strong>di</strong>te ohmiche nei conduttori (primariamente) e delle per<strong>di</strong>te nel<br />
<strong>di</strong>elettrico (secondariamente).<br />
Esercitazioni <strong>di</strong> Propagazione L-A - Ing. Enrico Vitucci
Potenza complessa (5/5)<br />
‣ La formula <strong>di</strong> <strong>trasmissione</strong> della tratta ra<strong>di</strong>o è del tutto analoga, cambia solamente il<br />
significato delle grandezze A e G, che in questo caso sono rispettivamente<br />
l’attenuazione <strong>di</strong> spazio libero e la somma dei guadagni g delle antenne.<br />
Si noti che le per<strong>di</strong>te ohmiche dovute alla natura imperfetta dei conduttori possono<br />
dar luogo ad attenuazioni estremamente elevate, anche in spezzoni <strong>di</strong> linea <strong>di</strong><br />
<strong>trasmissione</strong> non eccessivamente lunghi!<br />
necessità <strong>di</strong> sta<strong>di</strong> <strong>di</strong> amplificazione interme<strong>di</strong>.<br />
Esempio: si consideri una linea in aria, in cui, alla frequenza f = 560 MHz, risulta<br />
α=0,115 m -1 e β=11,7 m -1 .Sihaα/β