Circuitos de Corrente Alternada (CA) - DEMAR

Circuitos de Corrente Alternada (CA)
Circuitos resistivos e capacitivos
Introdução
Neste capítulo, faremos a análise de circuitos de corrente alternada (abreviado por CA
ou AC, em inglês), que são os circuitos constituídos por componentes alimentados por fontes
de tensão ou corrente alternada.
Em contraste com a corrente contínua CC, que tem amplitude constante, a corrente
alternada CA tem amplitude dependente do tempo. Na maioria dos casos segue a forma de
uma onda senoidal ou harmônica. Na sua origem, o sinal senoidal é produzido no gerador
elétrico através da movimentação de uma bobina de cobre dentro de um campo magnético,
causando a indução de uma tensão CA. A freqüência é de 60 ciclos/s (Hz), podendo existir
também sistemas de geração em 50 Hz. À partir da tensão CA são obtidas os outros tipos de
tensões/correntes elétricas que, doravante serão denotados por sinais.
Tipos de Sinais
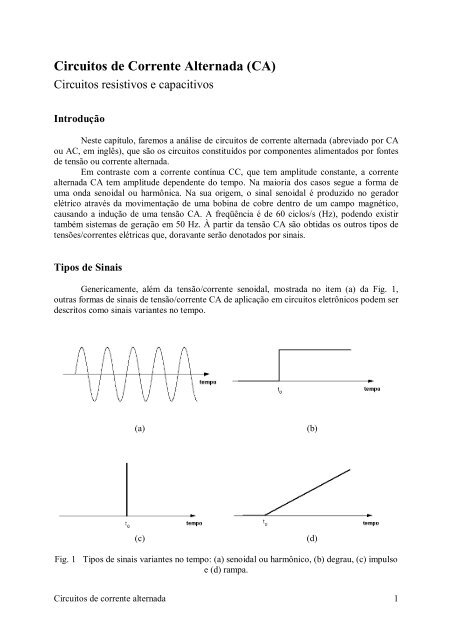
Genericamente, além da tensão/corrente senoidal, mostrada no item (a) da Fig. 1,
outras formas de sinais de tensão/corrente CA de aplicação em circuitos eletrônicos podem ser
descritos como sinais variantes no tempo.
(a)
(b)
(c)
(d)
Fig. 1 Tipos de sinais variantes no tempo: (a) senoidal ou harmônico, (b) degrau, (c) impulso
e (d) rampa.
Circuitos de corrente alternada 1

Sinal Senoidal
O sinal senoidal, também conhecido por sinal harmônico, é freqüentemente
encontrado em sinais de alimentação de energia, por causa das características do sistema de
geração e transmissão de energia elétrica. Uma onda senoidal com amplitude e freqüência
característicos são as informações que um sinal senoidal possui. A Fig. 2 apresenta um sinal
de tensão senoidal, com amplitude V p e período T. A relação entre o período T e a freqüência
f é determinado pela expressão:
1
f = (1)
T
Por questão de normalização, define-se a freqüência angular ω como:
ω = 2 πf
(2)
V
V p
0
0
π
2
π
3 π 2 π
2
ω t
-V p
T = período
Fig. 2 Sinal senoidal
Um sinal de tensão senoidal (conforme convenção da Fig. 2) pode ser descrito pela
expressão:
V = Vp sen ωt
(3)
Uma outra quantidade que está relacionada com o tipo de sinal senoidal é o ângulo de
fase, que corresponde à diferença na escala de tempo entre duas ondas senoidais de mesma
freqüência, como mostra a Fig. 3.
Se considerarmos o ângulo de fase φ na equação da tensão senoidal, resulta:
V = Vp sen( ωt
+ φ)
(4)
Circuitos de corrente alternada 2

V
V 1 V 2
0
ω t
φ
Fig. 3 Ângulo de fase φ entre dois sinais de tensão de mesma freqüência.
Forma Complexa de Representação da Onda Senoidal
Por questão de conveniência, a representação matemática da equação (4) pode ser
ampliada para a forma complexa:
V = V e
p
j( ωt+φ)
= V [cos( ωt
+ φ)
+ jsen( ωt
+ φ)]
p
(5)
na qual j = −1
.
Diagrama Fasorial
A representação gráfica de sinais senoidais de mesma freqüência com diferença de
fase é feita através do diagrama de Argand, utilizado para representar quantidades numéricas
do conjunto dos números complexos.
Im {V}
| V |sen φ
V | |
0
φ
- φ
| V | cos φ
Re {V}
- | V | sen φ
| V |
Fig. 4 Diagrama fasorial
representando no plano
complexo as componentes
real (Re) e imaginária (Im) da
tensão harmônica V.
Circuitos de corrente alternada 3

Circuito Resistivo CA
i
V
S
R
Fig. 5 Circuito resistivo
Sendo a tensão de alimentação expressa como:
V
S
= V sen ωt
p
ao aplicar a lei de Ohm ao resistor, V = Ri, resulta:
VS
i =
R
Vp
= sen ωt
R
A potência, calculada pela expressão P = Vi, fornece a seguinte expressão:
P = V i
p
p
pela qual, como sen 2 ωt ≥ 0, a potência instantânea P(t) será sempre ≥ 0, como mostra o
gráfico da potência da Fig. 6.
Da Matemática, temos a relação:
1
sen 2 x =
2
sen
2
ωt
( 1−
cos2x)
de onde se conclui que a forma da potência instantânea terá uma freqüência dobrada em
relação às freqüências da tensão e corrente instantâneas e, inversamente, o período da
potência será metade do período da tensão e da corrente instantâneas, como pode ser
observado nos gráficos da Fig. 6.
Circuitos de corrente alternada 4

V S
V p
0
0
__ π π 3__
π 2π
5__
π 3π
7__
π 4π
2
2
2
2
9__
π 5π
2
ω t
-V p
i
V p / R
0
0 __ π
2
π
3__
π 2π
5__
π 3π
7__
π 4π
9__
π 5π
2
2
2
2
ω t
-V p / R
P
V p
i p
V p
i p ____
2
0
0
__ π π 3__
π 2π
5__
π 3π
7__
π 4π
2
2
2
2
9__
π 5π
2
ω t
Fig. 6 Diagramas de tensão, corrente e potência versus tempo para o circuito resistivo puro.
A potência média P m é calculada pela fórmula:
de modo que a potência média do circuito resistivo vale
T
1
P
m
= ∫ P(t) dt
(7)
T
0
2π
1
2
Pm = Vpi
p
sen ωt.dωt
=
2π
∫
0
V i
p
2
p
Na forma complexa,
V
jωt
S
= Vpe
, obtendo-se a partir da lei de Ohm:
Circuitos de corrente alternada 5

VS
i =
R
Vp
= e
R
j ω t
=
i
p
e
jωt
de modo que o resistor como elemento de circuito CA não introduz defasagem entre a tensão
e a corrente. A Fig. 6 mostra que as curvas de tensão e corrente para o resistor estão em fase,
isto é, φ = 0. A Fig. 7 apresenta o diagrama fasorial para a tensão e a corrente.
i
V
Fig. 7 Fasores representando a tensão e a corrente sobre o resistor.
Capacitância
A capacitância elétrica é a medida da capacidade de armazenamento de cargas
elétricas por um dispositivo (Fig. 8) e é definida pela equação:
na qual:
ε – permitividade elétrica do meio material entre as placas (C/V.cm)
d – distância entre as placas do capacitor (cm)
A - área da placa (cm 2 )
A
C = ε
(8)
d
A
d
Fig. 8 Placas planas paralelas para o cálculo da capacitância.
Para materiais isolantes, também chamado de materiais dielétricos, a permitividade é
expressa em termos da permitividade no vácuo ε 0 (= 8,854.10 -12 C/V.m) multiplicada pela
constante dielétrica do material κ:
ε = ε0 κ
(9)
A constante dielétrica κ também é chamada permissividade relativa ε r .
A Tabela 1 apresenta a constante dielétrica e a rigidez dielétrica, que é a medida da
tensão elétrica que um material isolante é capaz de suportar sem conduzir corrente, para
diversos materiais isolantes.
Circuitos de corrente alternada 6

TABELA 1 – Constante dielétrica e rigidez dielétrica para alguns materiais isolantes
Material
Alumina Al 2 O 3 (99,9%)
Alumina (99,5%)
Berília BeO (99,5%)
Cordierita
Nylon 66 reforçado com 33%
de fibra de vidro (seco)
Nylon 66 reforçado com fibra
de vidro (50% umidade)
Poliéster
Constante dielétrica
κ
10,1
9,8
6,7
4,1-5,3
3,7
7,8
3,6
Rigidez dielétrica
(kV/mm)
9,1
9,5
10,2
2,4-7,9
20,5
17,3
21,7
A unidade de capacitância no SI é o farad (F), geralmente sendo utilizado frações
desta quantidade como µF (10 -6 F), nF (10 -9 F) e até pF (10 -12 F).
Capacitores
Capacitores são disponíveis em diversos tipos e valores. O valor da capacitância é
determinado pela constante dielétrica do material, da sua espessura e da área dos eletrodos. As
técnicas construtivas também diferem, dependendo do material dielétrico empregado. A Fig. 9
apresenta alguns arranjos construtivos empregados na fabricação de capacitores.
METAL
DIELÉTRICO
DIELÉTRICO
FOLHA
METÁLICA
DIELÉTRICO
Fig. 9 Arranjos construtivos para capacitores
As simbologias utilizadas para representar esquematicamente os capacitores estão
mostradas na Fig. 10.
Circuitos de corrente alternada 7

- +
- +
Fig. 10 Símbolos para o capacitor.
A Fig. 11 apresenta os principais tipos de capacitores comerciais e a Tabela 2 lista as
suas propriedades. Os maiores valores de capacitância são aqueles para os capacitores
eletrolíticos
ADVERTÊNCIA
Risco de
explosão !
Capacitores eletrolíticos não podem ser
ligados com terminais de polaridade
invertida, sob risco de explodirem !
Fig. 11 Tipos de capacitores
Circuitos de corrente alternada 8

TABELA 2 – Propriedades de capacitores comerciais
Tipo Material dielétrico Faixa de capacitância Tensão máxima
Variável ar 5 a 500 pF 500 V
Cerâmico Titanato de bário 1000 pF a 1 µF 2000 V
Óleo Papel com óleo 0,01 a 1 µF 10000 V
Mica Mica 100 a 5000 pF 10000 V
Filme
Eletrolítico
- Tântalo
- Alumínio
Chip
Mylar, Teflon,
poliestireno,
policarbonato
0,01 a 50 µF 1000 V
Óxido de tântalo
Óxido de alumínio
0,01 a 3000 µF
0,1 a 100000 µF
*
*
cerâmica
* A máxima tensão que pode ser aplicada a um capacitor eletrolítico depende do valor da capacitância. Por
exemplo, para 100.000 µF, uma tensão de 3 V pode danificar o capacitor, enquanto que para 100 µF, o
mesmo tipo de capacitor pode suportar 400 V.
Internamente, dependendo da sua construção, o capacitor apresenta resistências e
indutâncias, que interferem no comportamento do capacitor em função da freqüência de
trabalho. A Fig. 13 apresenta o circuito equivalente real de um capacitor, no qual as
resistências representam a fuga de corrente, isto é, a perda de carga por caminhos de baixa
resistência no interior e na superfície do capacitor, e a indutância L representa a variação da
corrente de fuga. Como a capacitância e a corrente de fuga são diretamente proporcionais à
área do capacitor, a resistência R P é inversamente proporcional à capacitância. Os fabricantes
geralmente classificam seus capacitores pelo produto de R P e C, em unidades de ohms ×
farads ou megohms × microfarads. Se convertermos o produto à unidade básica, veremos que,
1volt
1coulomb
1 ohm×
1 farad =
⋅ = 1 segundo
1coulomb / segundo 1volt
A quantidade definida pelo produto R P C é denominado tempo de fuga de corrente do
capacitor; quanto maior o seu valor, melhor será a capacidade do capacitor armazenar a carga.
A Tabela 3 apresenta os valores de tempo de fuga para diversos materiais dielétricos
comumente empregados na confecção de capacitores comerciais.
I L
R
S
V CC
C
L
C
R
P
Fig.13 Circuito equivalente do capacitor
Circuitos de corrente alternada 9

TABELA 3 – Tempos de fuga de corrente para alguns materiais dielétricos
Material MΩ × µF (25 o C)
Teflon
2.10 6
Poliestireno
1.10 6
Policarbonato
2.10 5
Mylar
1.10 5
Vidro
1.10 3 a 1.10 5
Mica
1.10 3 a 1.10 5
Papel
1.10 3 a 1.10 5
Cerâmica
1.10 3 a 1.10 5
Eletrolítico
10 a 1000
Analisando-se os valores da Tabela 3, pode-se concluir que um capacitor de
poliestireno é muito superior ao capacitor de papel, com base nos valores de tempo de fuga.
Naturalmente, o custo do capacitor é diretamente proporcional ao tempo de fuga, como
também ao valor da capacitância.
Análise de circuito com capacitor ideal
Um circuito contendo uma fonte de tensão senoidal acoplado a um capacitor ideal, isto
é, que contém somente capacitância, é mostrado na Fig. 14.
i
V
S
C
Fig. 14 Circuito com capacitor ideal
Sendo a tensão de alimentação expressa como
V
S
= V sen ωt
e sabendo que a
equação que relaciona a tensão V com a carga do capacitor q na forma q = CV, vem que:
i =
dq
dt
=
dV
C
dt
=
d
C
dt
V sen ωt
= ωCV
cosωt
o
Mas, cosω
t = sen( ωt
+ 90 ) , de mod que podemos re-escrever a equação para a corrente
instantânea como:
i(t) = ωCVp
sen( ωt
+ 90
p
o
)
p
p
Circuitos de corrente alternada 10

Dessa expressão, pode-se observar que a corrente está “adiantada” 90 o em relação à
tensão e o ângulo de fase φ = 90 o .
A potência, calculada pela expressão P = Vi, fornece a seguinte expressão:
P = ωCV
2
p
1
sen ωt.cosωt
= ωCV
2
2
p
sen 2ωt
A Fig. 15 mostra as formas de onda para a tensão, corrente e potência para o circuito
capacitivo puro. Pode-se observar novamente que a forma de onda da potência instantânea
tem uma freqüência que é o dobro da freqüência da tensão e corrente instantâneas.
V S
V p
0
0
__ π π 3__
π 2π
5__
π 3π
7__
π 4π
2
2
2
2
9__
π 5π
2
ω t
-V p
i
ωCV p
0
0 __ π
2
π
3__
π 2π
5__
π 3π
7__
π 4π
9__
π 5π
2
2
2
2
ω t
-ωCV p
P
2
ωCV
____ p
2
0
0
__ π π 3__
π 2π
5__
π 3π
7__
π 4π
2
2
2
2
9__
π 5π
2
ω t
2
ωCV
____ p
2
Fig. 15 Diagramas de tensão, corrente e potência versus tempo para o circuito capacitivo.
Circuitos de corrente alternada 11

A potência média pode ser calculada para meio ciclo (neste caso, π/2), a partir da
equação
T / 2
π / 2
1
1 1 2
2
P
m
= P(t).dt
CVp
sen 2 t.dt 2fCVp
T / 2
∫ = ω ω =
π / 2
∫
.
2
0
0
Na forma complexa, sendo a tensão expressa como
determinada pela equação
i = CdV / dt
, obtém-se:
V
S
jωt
= Vpe
e sendo a corrente
Na forma inversa,
i =
d
C
dt
V e
p
V S
jωt
= jωCV e
p
jωt
1 j
= i = − i
jωC
ωC
= jωCV
S
Esta equação mostra a vantagem de se adotar a forma complexa, pelo fato de explicitar
a relação algébrica da tensão com a corrente por uma constante de proporcionalidade –j/ωC,
tal como a lei de Ohm expressa a relação da tensão com a corrente com a resistência como
constante de proporcionalidade para circuitos resistivos. De fato, a constante –j/ωC é
fisicamente análoga à resistência, e é denominada de impedância capacitiva Z C e tem
dimensão de resistência (ohm):
Z C
j
= − (Ω)
ωC
A Fig. 16 apresenta a representação gráfica dos fasores de tensão e corrente para o
capacitor, com ângulo de fase φ = 90 o .
i
φ = 90 o
V
Fig. 16 Fasores representando a tensão e a corrente sobre o capacitor.
Uma outra forma de representar os fasores é a chamada forma polar, pela qual a tensão
V S é apresentada com o seu valor eficaz V ef e o ângulo de fase φ como:
V V ∠φ
(10)
S
= ef
O valor eficaz V ef ou valor quadrático médio (rms – root mean square) de uma
quantidade V S é definido pela expressão:
Circuitos de corrente alternada 12

T
1 2
V
ef
= Vrms
= ∫ Vs
dt
(11)
T
Para uma tensão senoidal V S = V p sen ωt, o valor eficaz pode ser calculado como:
0
V
ef
2π
1
= V
2π
∫
0
2
p
sen
2
ωtdt
=
V
p
2
≅ 0,707V
p
Para efeito de comparação, vamos calcular o valor médio da tensão, V m , calculado
sobre meio-ciclo:
V
m
T
2
π
2 1
= VSdt
T
∫ =
π∫
0
0
2Vp
Vp
sen ωt
=
π
≅ 0,637V
p
Assim, a relação entre os valores de pico V p , o valor eficaz V ef e o valor médio V m ,
para uma função senoidal, é:
V = 1,414V = 1,571V
p
ef
m
O diagrama da Fig. 17 ilustra a comparação entre os valores característicos de uma
onda senoidal.
V
V p
0,707 V p
0,637 V p
V p Vpp
V V
m ef
0
ω t
-V p
Fig. 17 Relações entre os valores característicos para uma onda senoidal.
Circuito RC série
Faremos agora a análise de circuitos contendo um resistor em série com um capacitor,
conforme mostra a Fig. 18.
Circuitos de corrente alternada 13

R
V i
Fig. 18 Circuito RC em série
+
-
i
C
Dependendo de onde será conectado o terminal de saída da tensão, o circuito RC série
recebe o nome de circuito RC integrador ou diferenciador, ou então, respectivamente, circuito
filtro passa-baixa e circuito filtro passa-alta.
Circuito RC Integrador
Na forma esquemática mais conveniente.
V
i
R
i
C
V
o
Fig. 19 Circuito RC esquemático
Aplicando a lei de Kirchhoff ao circuito da Fig. 19:
na qual:
e
V i
= Ri + q / C
(12)
i = dq / dt
(13)
V o
= q / C
(14)
Re-escrevendo (12) na forma diferencial:
dq q Vi
+ =
(15)
dt RC R
Esta equação diferencial possui soluções dependentes da função V i , que analisaremos
para os principais casos.
Circuitos de corrente alternada 14

Resposta ao Degrau
Consideremos a função V i como a função degrau, definida matematicamente como:
⎧ 0,
t ≤ 0
Vi = ⎨
(16)
⎩V
S , t > 0
o que representa uma excitação constante V 0 a partir do instante inicial t = 0. O gráfico da
Fig. 20 apresenta a função degrau.
Vi
V
S
0 t = 0
t
Fig. 20 Gráfico da função degrau
Em t = 0, a carga acumulada no capacitor é igual a zero e a equação diferencial pode
ser integrada como:
q
dq 1
=
∫ ( CV − q ) RC
0
S
t
∫
0
dt
(17)
A solução da integral da equação (6) é dada por:
que, rearranjada em termos de q(t), resulta em:
t
− q t
n( CVS
− q)
0 = RC
(18)
S
0
−t
/ RC
( − e )
q( t ) = V C 1 (19)
A corrente i é calculada a partir da derivada de (19), de modo que:
dq V S −t
/ RC
i = = e
(20)
dt R
De (19) também pode-se calcular a tensão V o :
V
o
−t
/ RC
( − e )
q
= = VS
1 (21)
C
Circuitos de corrente alternada 15

O termo exponencial apresenta o denominador RC, cuja dimensão é de tempo. O
produto RC representa a constante de tempo para o circuito resistor-capacitor e significa o
tempo que um capacitor leva para atingir 0,632V S (= 1 - 1/e) da tensão em regime
estacionário durante o carregamento. Se o circuito estiver descarregando, a constante de
tempo RC representa o tempo que leva para a tensão atingir 36,8% do seu valor inicial.
As Figuras 21 e 22 apresentam as curvas de tensão e corrente em função do tempo
normalizado pela constante RC, durante o carregamento do capacitor. Se considerarmos V 0
como a tensão em regime estacionário (para t → ∞), na Fig. 21, para t = RC, o valor da tensão
normalizada será V/V 0 = 0,632; para t = 2RC, V/V 0 = 0,865, isto é, a tensão será 86,5% da
tensão V 0 ; em t = 3RC, V/V 0 = 0,95; em t = 4RC, V/V 0 = 0,982 e em t = 5RC, V/V 0 = 0,993,
isto é, a tensão terá atingido 99,3% do valor estacionário.
1,0
Tensão normalizada V/V 0
0,8
0,632
0,6
0,4
0,2
0,0
0 1 2 3 4 5 6 7
tempo em constante RC (s)
Fig. 21 Curva de tensão em função do tempo para o circuito RC integrador.
1,0
Corrente normalizada, i/i 0
0,8
0,6
0,4
0,368
0,2
0,0
0 1 2 3 4 5 6 7
tempo em constante RC (s)
Fig. 22 Curva da corrente em função do tempo para o circuito série RC.
Circuitos de corrente alternada 16

Filtro Passa-Baixa (Resposta Senoidal)
Como visto anteriormente, a resposta de um circuito RC à excitação senoidal produz
um sinal de tensão defasado 90 o em relação à corrente. Se aplicarmos a análise na forma
fasorial, teremos a impedância:
Z = R + jX C
(22)
na qual, para um circuito RC
X C
= −1 / ωC
é denominada reatância capacitiva, de modo que
Z
j
= R −
(23)
ωC
Em notação polar,
Z = | Z | ∠ − arctg (| X C | / R ) = | Z | ∠ − arctg ( 1 / ωRC ) (24)
2
2
2
na qual | Z | = R + 1/
ω C é chamada amplitude da impedância. Sendo a tensão de
excitação dada por:
i V ef
na qual V ef é o valor da tensão de excitação eficaz.
A corrente é calculada por:
o
V = ∠0
(25)
Vi
I =
Z
o
V1 ∠0
=
(26)
| Z | ∠ − arctg (| X | / R )
C
na qual as equações (24) e (25) foram usadas. Re-escrevendo a equação (26) na forma polar:
Vef
I = ∠arctg(|
X C | / R )
(27)
| Z |
A impedância do capacitor é definida como:
1 o
ZC
= ∠ − 90
(28)
ωC
pela qual, podemos calcular a tensão de saída V out como:
o
[ | X ∠ − ]
⎡Vef
⎤
Vo = IZC
= ⎢ ∠arctg(|
X C | / R ) ⎥ ⋅ C | 90
⎣|
Z |
⎦
Circuitos de corrente alternada 17

| X C |Vef
o
= ∠ − 90 + arctg (| X C | / R )
(29)
| Z |
Resumindo, a amplitude da tensão de saída é:
e o ãngulo de fase φ:
Vef
| X C |
Vo =
| Z |
(30)
o ⎛ 1 ⎞
φ = −90 + arctg ⎜ ⎟
⎝ ωRC
⎠
(31)
Para analisarmos a resposta do circuito RC à excitação senoidal é conveniente
expressarmos a razão entre a amplitude da tensão de saída V out e a amplitude da tensão de
entrada V in :
V
V
o
i
=
R
1
ωC
1
=
2
2 2 2
+ ω R C +
2 2
ω
C
1
1
(32)
Esta razão é denominada ganho de tensão do circuito e é utilizada para avaliar o
desempenho de circuitos. Tomando-se os valores R = 1 kΩ e C = 1 µF, foram calculados os
valores mostrados na Tabela 4. O gráfico do ângulo de fase φ versus a freqüência angular ω é
mostrada na Fig. 23, enquanto que a Fig. 24 apresenta o gráfico do ganho de tensão versus ω.
Este circuito, com estas características, é chamado filtro passa-baixa, porque ele deixa passar
sinais de baixa freqüência com pequena ou nenhuma atenuação. À medida que a freqüência, a
atenuação aumenta consideravelmente.
TABELA 4 Resposta em freqüência para o filtro passa-baixa.
R = 1 kΩ, C = 1 µF
ω (rad/s) f (Hz) log ω φ (graus) V o /V i log(V o /V i )
1 0,16 0 -0,06 1 0,00000
10 1,6 1 -0,57 0,99995 -0,00002
100 15,9 2 -5,71 0,99504 -0,00216
200 31,8 2,3 -11,31 0,98058 -0,00852
1000 159,2 3 -45,00 0,70711 -0,15051
10000 1591,5 4 -84,29 0,0995 -1,00216
50000 7957,7 4,7 -88,85 0,0200 -1,69906
100000 15915,5 5 -89,48 0,0100 -2,00002
500000 79577,5 5,7 -89,89 0,0020 -2,69897
1000000 159154,9 6 -89,94 0,0010 -3,00000
Circuitos de corrente alternada 18

0
-10
Ângulo de fase, φ (graus)
-20
-30
-40
-50
-60
-70
-80
-90
0 1 2 3 4 5 6
log ω
Fig. 23 Ângulo de fase versus freqüência angular para o filtro passa-baixa.
0
log ω C
= 3
-1
-1
log(V o
/V i
)
-2
-2
-3
-3
0 1 2 3 4 5 6
log ω
Fig. 24 Ganho de tensão versus freqüência angular para o filtro passa-baixa.
A freqüência na qual R = |X C | é chamada freqüência de corte, f C :
f C
1
= (33)
2πRC
Para o circuito analisado, f C = 159,2 Hz
Circuito RC Diferenciador
O circuito RC série também pode ser utilizado como circuito diferenciador,
arranjando-se o resistor e o capacitor segundo o esquema ilustrado na Fig. 25.
Circuitos de corrente alternada 19

C
V
i
V
o
i
R
Fig. 25 Circuito RC diferenciador
Neste circuito, a tensão V o é determinada pela tensão sobre o resistor:
V o = Ri
(34)
Se considerarmos o estímulo da função degrau, a equação (15) combinada com a
equação (16) resultará em:
V
o
S
−t
/ RC
= V e
(35)
que corresponde a um decaimento exponencial da tensão com o incremento de tensão do
degrau. Observe que este comportamento é o inverso do circuito integrador, calculado na
equação (21). A Fig. 26 apresenta o gráfico da curva de tensão V o em função do tempo
normalizado para o circuito diferenciador.
1,0
0,8
Tensão normalizada V/V 0
0,6
0,4
0,2
0,0
0 1 2 3 4 5 6 7
tempo em constante RC (s)
Fig. 26 Curva de tensão em função do tempo para o circuito RC diferenciador.
Filtro Passa-Alta (Resposta Senoidal)
O circuito da Fig. 25 também é utilizado como filtro passa-alta, isto é, um filtro que
atenua os sinais de baixa freqüência. Para este circuito, a tensão V out , calculada sobre o
resistor em notação fasorial polar, é descrita por:
Circuitos de corrente alternada 20

o
[ R∠
]
⎡Vef
⎤
Vo
= IR = ⎢ ∠arctg(|
X C | / R ) ⎥ ⋅ 0
⎣|
Z |
⎦
VS
R
= ∠arctg(|
X C | / R )
(36)
| Z |
A amplitude do ganho é expressa como:
V
V
o
i
=
R
R
=
ωRC
2 1 2 2 2
+ ω R C +
2 2
ω
C
1
(37)
e o ãngulo de fase φ:
⎛|
X
φ = arctg ⎜
⎝ R
| ⎞ ⎛ ⎞
⎟ = arctg ⎜ ⎟
⎠ ⎝ ωRC
⎠
C 1
(38)
A freqüência de corte é a mesma para o circuito integrador, ou seja
f C
= 1 / 2πRC
=
159 Hz. A resposta do filtro passa-alta para R = 1 kΩ e C = 1 µF está apresentado na
Tabela 5, enquanto que as curvas de resposta em freqüência do ganho de tensão e do ângulo
de fase estão mostradas, respectivamente, nas Figuras 27 e 28.
Observar que as curvas para o filtro passa-alta são imagens invertidas das curvas para
o filtro passa-baixa. A interseção das curvas de ganho de tensão com o eixo x conduz ao
mesmo valor da freqüência de corte f C , como tinhamos observado no cálculo analítico. Isto
significa que o dimensionamento de um filtro RC passa-baixa ou passa-alta pode ser feita
simplesmente conhecendo-se os valores de R e C.
Considere a possibilidade de inserir um filtro passa-baixa em série com um filtro
passa-alta, como ilustrado na Fig. 29. Dependendo dos valores de resistência e capacitância
empregado nos dois filtros, podemos estabelecer uma faixa de freqüências na qual o sinal de
saída será levemente atenuado e fora dessa faixa o sinal será fortemente atenuado. A este tipo
de filtro dá-se o nome de filtro passa-faixa ou filtro passa-banda.
TABELA 5 Resposta em freqüência para o filtro passa-alta.
R = 1 kΩ, C = 1 µF
ω (rad/s) f (Hz) log ω φ (graus) V o /V i log(V o /V i )
1 0,16 0 89,94 0,001 -3,00000
10 1,6 1 89,43 0,010 -2,00002
100 15,9 2 84,29 0,0995 -1,00216
200 31,8 2,3 78,69 0,1961 -0,70749
1000 159,2 3 45,00 0,7071 -0,15051
10000 1591,5 4 5,71 0,9950 -0,00216
50000 7957,7 4,7 1,15 0,9998 -0,00008
100000 15915,5 5 0,57 0,99995 -0,00002
500000 79577,5 5,7 0,11 1,00000 0
1000000 159154,9 6 0,06 1,00000 0
Circuitos de corrente alternada 21

0
log ω C
= 3
-1
-1
log(V o
/V i
)
-2
-2
-3
-3
0 1 2 3 4 5 6
log ω
Fig. 27 Ganho de tensão versus freqüência angular para o filtro passa-alta.
90
80
Ângulo de fase, φ (graus)
70
60
50
40
30
20
10
0
0 1 2 3 4 5 6
log ω
Fig. 28 Ângulo de fase versus freqüência angular para o filtro passa-alta.
Filtro Passa-Banda (Resposta Senoidal)
Se combinarmos um circuito RC passa-baixa em série com um circuito RC passa-alta,
teremos um circuito RC que desempenha o papel de um filtro passa-banda, conforme mostra
a Fig. 29. A característica de um filtro passa-banda é o de atenuar a amplitude do sinal cuja
freqüência esteja fora da banda passante, isto é, das freqüências que estejam abaixo da
freqüência de atenuação do circuito do filtro passa-alta e acima da freqüência de atenuação do
circuito do filtro passa-baixa.
Circuitos de corrente alternada 22

R
C
V in
V out
C
R
Fig. 29 Circuito do filtro passa-banda.
Circuitos de Corrente Alternada
Circuitos indutivos
Indutância
A indutância elétrica é a medida da capacidade de armazenamento de corrente elétrica
por um dispositivo, geralmente com formato de bobina (Fig. 30), conhecido também como
indutor. A indutância é definida pela equação:
na qual:
L = φ
(40)
i
L – indutância da bobina (henry = H)
φ – fluxo magnético que atravessa a área interna da bobina (Wb = T.m 2 )
i – corrente que percorre as espiras da bobina (A)
Indução magnética
→
B
i
i
Linhas de fluxo magnético
Fig. 30 Esquema do indutor.
Circuitos de corrente alternada 23

A equação (40) é válida para indutores com núcleo de ar, para os quais a
permeabilidade magnética é constante e igual a µ 0 = 4π.10 -7 T.m/A. No caso de indutores com
núcleo magnético, a indutância é calculada a partir da derivada do fluxo pela corrente:
dφ
L = (41)
di
O elemento de circuito indutor opera sob a ação de corrente ou tensão variável, que
produzem um campo magnético variável
(a)
(b)
Fig. 31 Símbolos para o indutor (a) com núcleo de ar e (b) com núcleo de ferro.
A equação (41) pode se re-escrita como:
de modo que,
dφ
dt
L = ⋅
(42)
dt di
d φ di = L
dt dt
(43)
Sabendo-se pela lei de Faraday do Eletromagnetismo que a variação de fluxo no
tempo induz uma diferença de potencial V no circuito elétrico, a equação (43) pode ser escrita
como:
di
V = L
(44)
dt
A potência de um circuito contendo um indutor pode ser calculada como:
2
di 1 di
P = Vi = Li = L
(45)
dt 2 dt
A energia armazenada na forma de campo magnético no indutor pode ser calculada
tomando-se a corrente i = 0 em t = 0 até a corrente i no instante t qualquer:
t
i
di
1 2
E = Li dt = Li di = Li
(46)
∫ dt ∫ 2
0
0
Circuitos de corrente alternada 24

Transformador de tensão
O transformador é um elemento de circuito constituído por dois indutores acoplados
magneticamente por um núcleo de material ferromagnético, através do qual a energia de um
indutor é transferido a outro. As suas principais aplicações são para a elevação ou redução da
tensão ou corrente, com mínima dissipação de energia por envolver prioritariamente campo
magnético (campo não-dissipativo). Para as aplicações eletrotécnicas (50/60 Hz), geralmente
o núcleo é de ferro puro ou de ligas de ferro, especialmente de Fe-Si por apresentar baixas
perdas histeréticas. Para aplicações em altas freqüências o núcleo é constituído de material de
alta resistividade elétrica, como os ferritas, de modo a minimizar as perdas por correntes
parasitas.
A Fig. 32 mostra os símbolos do transformador com núcleo de ar e com núcleo de
ferro.
Fig. 12
(a)
Símbolo para o transformador (a) com núcleo de ar e (b) com núcleo de ferro.
(b)
Devido à importância de transformadores em circuitos eletrônicos e de
instrumentação, faremos o cálculo das relações entre tensão e corrente para um transformador.
Um transformador é um dispositivo magnetoelétrico constituído por dois enrolamentos
(um primário, o outro secundário) conectados magnéticamente pelo núcleo de material
magnético, conforme mostra a Fig. 33.
A C
: Área de seção transversal do núcleo
i 1
i 2
N
V V
1
2
2
Primário
Secundário
N
1
: Número de espiras
: Comprimento do circuito magnético
C
Fig. 33 Transformador com núcleo de ferro.
Para o cálculo das relações de tensão e corrente no transformador, consideremos
inicialmente a lei de Ampère:
Circuitos de corrente alternada 25

¢ ¢
H ⋅ d = i
∫ ¡
C
(47)
Admitindo H constante em £ C , então o campo magnético produzido pelo indutor 1
pode ser calculado à partir da integral de (47) como sendo:
N1i1
H = (48)
C
£
O fluxo magnético induzido no núcleo de ferro é dado por:
φ = B .A = µ H.A C
(49)
O fluxo magnético produzido pelo indutor 1:
µ N i A
φ = 11
C
(50)
£ C
Derivando o fluxo no tempo:
dφ
µ N A di
= 1 C ⋅ 1
dt C dt
£
(51)
de modo que:
di 1 = C
dt µ
£
N1AC
dφ
⋅
dt
(52)
Se considerarmos a resistência elétrica do condutor desprezível, então:
di
V = L⋅
1
1
dt
= L ⋅
£ C
µ N1AC
dφ
⋅
dt
(53)
Considerando que a indutância de um toróide pode ser calculada como:
2
µ N A
L = C
(54)
C
£
que, substituindo em (53), resulta na equação:
Circuitos de corrente alternada 26

dφ
V 1 = N 1 ⋅
(55)
dt
Embora esta equação tenha sido calculada para um núcleo toroidal, ela pode ser
generalizada para qualquer geometria de núcleo, contanto que o fluxo enlaçado pelo núcleo
não sofra espraiamento e seja constante em C .
A tensão induzida no indutor 2 será gerada pela variação do fluxo magnético dφ/dt no
circuito magnético. Para calculá-la, vamos utilizar a lei de Faraday.
∫
m
dφ
E ⋅ d =
(56)
¢ dt
¡ ¢
onde m é o comprimento de uma espira no circuito 2.
Considerando que o circuito magnético possui elevada permeabilidade, ou seja,
dφ d d
φ1 = φ2
= φ e, consequentemente, 1 φ φ
= 2 =
dt dt dt
, de modo que:
ou seja,
N
dφ
E ⋅ d = V = N ⋅
∫ 2 2
(57)
¢ dt
2 ¡ ¢
m
dφ
V 2 = N 2 ⋅
(58)
dt
À partir das equações (55) e (58), podemos escrever a relação entre as tensões V 2 e V 1 :
V 2 N =
2
(60)
V1
N1
Para o cálculo da relação entre as correntes i 2 e i 1 ., podemos considerar que o fluxo
nos dois indutores é aproximadamente idêntico, de modo que:
da qual vem que:
ou seja:
µ N1 i1
AC
µ N 2i2
AC
=
(61)
C
C
N 1i1
= N2i2
(62)
i2
N1
=
i1
N 2
(63)
Circuitos de corrente alternada 27

As equações (60) e (63) são empregadas para o cálculo de um transformador ideal, isto
é, um transformador para o qual:
(a) O fluxo da bobina secundária é totalmente enlaçado pelo fluxo na bobina primária;
(b) Não há perdas no ferro e nem nos condutores;
(c) O núcleo não está saturado e a sua permeabilidade magnética é linear com relação ao
campo magnético H.
Podemos observar que quando o número de espiras no primário é maior do que no
secundário, o transformador abaixa a tensão e eleva a corrente no secundário e vice-versa.
Circuitos RL
O elemento de circuito indutor é comumente empregado juntamente com o resistor
como filtro para sinais de alta freqüência em analogia com os circuitos RC e também na
modelagem de circuitos de potência como motores , geradores e transformadores, acoplados a
cargas resistivas.
R
V i
L
i
Fig. 34
Circuito RL em série
A equação que descreve o circuito da Fig. 34 pode ser expressa como:
di
Ri + L = V i
(64)
dt
Para obtermos a solução da equação diferencial ordinária (64), vamos estabelecer dois
tipos de estímulo em V i : a função degrau e a função senoidal. Enquanto no primeiro tipo de
estímulo vamos resolver analiticamente (64), no segundo tipo, o tratamento será o mesmo
aplicado para o circuito RC senoidal, isto é, solução por fasores.
Resposta do circuito RL série ao degrau.
Novamente, consideremos a função V i como
matematicamente como:
a função degrau, definida
Circuitos de corrente alternada 28

⎧ 0, t ≤ 0
Vi = ⎨
(65)
⎩VS
, t > 0
o que representa uma excitação constante V 0 a partir do instante inicial t = 0. O gráfico da
Fig. 35 apresenta a função degrau.
Vi
V
S
0 t = 0
t
Fig. 35
Gráfico da função degrau
Em t = 0, a corrente aplicada ao circuito é armazenada no indutor na forma de campo
magnético, em analogia à carga acumulada no capacitor no circuito RC. A equação diferencial
(64) pode ser integrada por separação de variáveis, como:
cuja solução é dada por:
na qual:
i
∫ di =
∫
⎛ Vs
⎞
⎜
0 ⎝ R
− i⎟
⎠
t
0
−t
/ τ
( 1 − e )
R
L
dt
(66)
Vs
i =
(67)
R
L
τ =
(68)
R
é a constante de tempo do circuito RL. A tensão sobre o indutor é calculada a partir da
equação:
di
dt
− / τ
V = =
t
L
L VSe
(69)
As Figuras 36 e 37 apresentam as curvas de corrente normalizada (i/i 0 , onde i 0 = V S /R)
e de tensão sobre o indutor normalizada (V L /V S ) versus tempo normalizado (t/τ). A resposta
do circuito RL é semelhante à do circuito RC para um estímulo na forma degrau. Entretanto,
algumas diferenças cumpre enfatizar: primeiro, a corrente vai de zero até o valor em regime,
pois quando a tensão degrau é aplicada, i = 0 e di/dt = máximo; segundo, a força eletromotriz
induzida sobre o indutor (V L ) é alta no início mas, à medida que V L diminui, a corrente
aumenta e, concomitantemente, di/dt decresce (pois, V L = Ldi/dt). Ambas as curvas
apresentam comportamento exponencial (crescimento na corrente e decaimento na tensão).
Circuitos de corrente alternada 29

No circuito RL, a constante de tempo τ = L/R determina a taxa de crescimento e de
decaimento da curva exponencial, de maneira análoga à constante τ = RC no circuito RC.
1,0
0,8
Corrente normalizada, i/i 0
0,6
0,4
0,2
0,0
0 1 2 3 4 5 6 7
tempo em constante τ = L/R
Fig. 36 Curva de corrente normalizada em função do tempo t/τ para o circuito RL em série.
1,0
Tensão normalizada, V L
/V S
0,8
0,6
0,4
0,2
0,0
0 1 2 3 4 5 6 7
tempo em constante τ = L/R
Fig. 37 Curva de tensão normalizada sobre o indutor para o circuito RL em série.
Resposta do circuito RL série à excitação senoidal.
O circuito RL comporta-se como um circuito divisor de tensão dependente da
freqüência. Para uma corrente de excitação senoidal (i L = i 0 sen ωt), a tensão V L sobre o
indutor aumenta com a freqüência, pois:
Circuitos de corrente alternada 30

V
di
o
= L = ωLi
0
cosωt
= ωLi
0
sen( ωt
90 )
(70)
dt
L
+
Esta equação estabelece que a tensão está adiantada 90 o em relação à corrente. Este
comportamento é exatamente o oposto ao do circuito capacitivo, no qual a tensão está
atrasada 90 o em relação à corrente.
A reatância indutiva X L é definida como:
X L
= ωL
(71)
A impedância de um indutor ideal é expressa como:
Z
L
= jX = jωL
(72)
L
que é representado em notação fasorial como:
Z
L
90
o
= X
L∠
(73)
Para um circuito RL em série, podemos desenvolver as expressões para o ganho de
tensão e para o ângulo de fase de maneira análoga ao circuito RC. Se o fasor de tensão V in for
expresso como:
e a impedância do circuito RL como:
V
o
in
= V1∠0
2 2
Z = R + jX = R + X ∠arctg(X
/ R)
(74)
L
L
L
Aplicando a expressão:
V
V = ZI ⇒ I = , resulta:
Z
V1 I = ∠ − arctg(X
L
/ R)
(75)
2 2
R + X
L
Como no circuito RC em série, a tensão de saída no circuito RL pode ser lida de duas
formas distintas: sobre o resistor (circuito integrador) e sobre o indutor (circuito
diferenciador), conforme mostrado na Fig. 38.
Circuitos de corrente alternada 31

V
in
L
V
out
V
in
R
V
out
i
R
i
L
(a)
Fig.38
Circuito RL (a) integrador e (b) diferenciador.
(b)
Quando a tensão é lida sobre o resistor, o ganho de tensão do circuito é dado por:
V
V
R
in
R R
R
= = ∠ − arctg(X
L
/ R) =
∠ − arctg( ωL / R) (76)
Z
2 2
2 2 2
R + X
R + ω L
L
A amplitude do ganho é calculada como:
e o ângulo de fase por:
V
V
R
in
R
= (77)
2 2 2
R + ω L
φ = −arctg(
ωL / R)
(78)
Quando a tensão é lida sobre o indutor, o ganho de tensão se torna:
V
V
L
in
ZL
X
L
o
ωL
o
= = ∠90
− arctg(X
L
/ R) =
∠90
− arctg( ωL / R) (79)
Z
2 2
2 2 2
R + X
R + ω L
L
A amplitude do ganho é calculada como:
e o ângulo de fase por:
V
V
L
in
=
ωL
(80)
2 2 2
R + ω L
φ = 90 o − arctg( ωL / R)
(81)
A potência consumida num indutor ideal é zero porque, como no caso do capacitor, o
ângulo de fase entre a tensão e a corrente é de 90 º . Para um indutor real, a potência consumida
é calculada a partir da resistência elétrica do fio utilizado no enrolamento da bobina.
Circuitos de corrente alternada 32

Como a reatância indutiva é dependente da freqüência e como um indutor real possui
resistência, uma propriedade denominada fator de qualidade Q de um indutor é definida e é
expressa como:
X
L
Q = (82)
R
Quanto maior o fator de qualidade para uma dada freqüência, menor será a resistência
elétrica da bobina.
Circuitos LC
Os circuitos LC são comumente empregados em filtros de alta freqüência e também
em circuitos sintonizados, principalmente em transmissão de sinais de rádio-freqüência. Eles
apresentam como principal característica a ressonância, isto é, a capacidade de amplificar um
sinal a uma dada freqüência de sintonia, daí o fato de serem largamente utilizados em
circuitos de recepção de sinais de rádio, nos quais os sinais fora da freqüência de ressonância
são filtrados e o sinal na freqüência de ressonância é ampliado.
Existem dois tipos de circuitos LC: série e paralelo. Ambos os circuitos são
constituídos por um capacitor e um indutor. A Fig. 39 apresenta os circuitos LC série e
paralelo.
L
C
L
C
(a) (b)
Fig. 39
Circuitos LC (a) série e (b) paralelo.
A ressonância ocorre quando as reatâncias indutiva e capacitiva forem iguais,
X L = X C , ou seja,
1
1
L
ω
2
ω = ⇒ =
(83)
ωC
LC
Para uma dada combinação de L e C, isto ocorrerá somente em uma única freqüência,
que pode ser calculada de (83), sabendo que f = ω/2π:
Circuitos de corrente alternada 33

f 0
1
= (84)
2π
LC
Chamamos de ressonância ou freqüência de ressonância, a freqüência de oscilação
própria do circuito. A física do processo de ressonância pode ser explicada em termos simples
através dos circuitos esquemáticos desenhados na Fig. 40.
Vamos supor que, inicialmente, uma tensão seja aplicada entre os terminais do
capacitor. Quando isto ocorrer, o capacitor se carregará (Fig. 40a). A energia armazenada no
capacitor na forma de energia elétrica U E é expressa como:
1
2
2
U
E
= CV
(85)
Consideremos, agora que o capacitor está carregado, que a tensão de alimentação seja
removida. Quando a tensão for retirada, o capacitor terá o potencial V, que conectado a um
indutor descarregado, tenderá a anular o potencial elétrico, gerando uma corrente através do
indutor (Fig. 40b). Esta corrente induzirá um campo magnético quando circular pelo indutor.
Quando o potencial no capacitor for zerado, toda a energia do circuito estará armazenada no
indutor na forma de energia magnética U B (Fig. 40c):
1
2
2
U
B
= Li
(86)
Quando a corrente cessar, o campo magnético começará a diminuir, criando assim por
indução nas espiras do indutor, uma corrente contrária à que lhe criou. Esta corrente carregará
o capacitor com polaridade contrária a anterior. Observe o sentido das setas das linhas
equipotenciais elétricas no capacitor nas Fig. 40d e 40e. Quando o campo magnético se findar,
a corrente deixará de circular e o capacitor estará carregado (Fig. 40e).
Novamente, o processo de descarga do capacitor e de carga do indutor é retomado
(Fig. 40f e 40g) e continuará assim, indefinidamente. Este tipo de circuito oscilador recebe o
nome de circuito tanque, pois os elementos capacitor e indutor agem como reservatórios de
energia. Na prática, circuitos LC são ideais, pois capacitores e indutores reais possuem perdas
e a dissipação da energia na forma de calor levará ao consumo da energia fornecida pela fonte
externa no início do processo.
Se medíssemos a variação de tensão sobre o capacitor ou o indutor veríamos um sinal
alternado de forma senoidal e freqüência própria de ressonância. Em freqüências inferiores e
superiores à freqüência de ressonância, a impedância do circuito LC série (Fig. 40a) aumenta,
enquanto que a corrente diminui. Da mesma forma, próximo ou igual à freqüência de
ressonância, a impedância diminui e a corrente aumenta.
Em circuitos ressonantes paralelo (Fig. 40b), próximo à freqüência de ressonância, a
impedância aumenta e a corrente diminui. No caso contrário, ou seja, quando a freqüência
estiver distante da freqüência de ressonância, a corrente aumentará e a resistência diminuirá.
Circuitos de corrente alternada 34

Fig. 40 Ciclo de oscilação de um circuito LC não-dissipativo. Os gráficos de barra
representam a energia magnética (U B ) e elétrica (U E ) armazenada, respectivamente, no
indutor e no capacitor (Halliday, 1993).
O grau com que estas mudanças ocorrem com freqüências superiores e inferiores a de
ressonância é uma medida de “habilidade” do circuito de separar (discriminar) freqüências.
Essa habilidade é calculada através do fator de qualidade do circuito, e que pode ser calculado
para circuitos indutivos e capacitivos:
X
Q =
L
ou
R
XC
Q = (87)
R
Acrescentando-se um resistor em série com o circuito série, ou em paralelo com o
circuito paralelo, aumenta-se a faixa de passagem ou, em outras palavras, diminui-se o Q.
Referências bibliográficas
DIEFENDERFER, A.J. Principles of electronic instrumentation. Philadelphia, PA: Sauders
College Publishing, 1979.
HALLIDAY, D., RESNICK, R., WALKER, J. Fundamentals of physics – Extended with
modern physics. New York: John Wiley, 1993.
Circuitos de corrente alternada 35