Die Boltzmann Verteilung

Die Boltzmann Verteilung
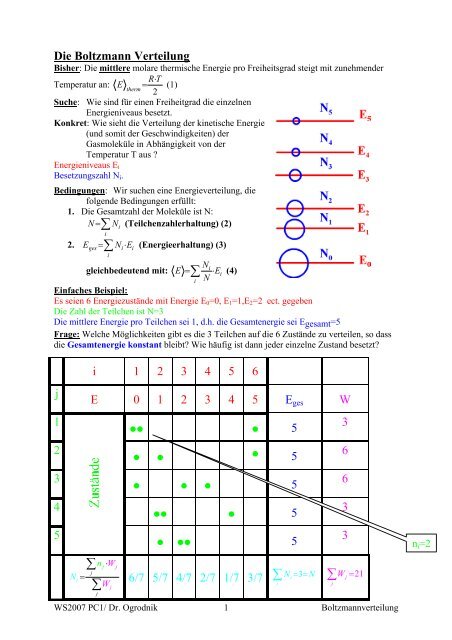
Bisher: Die mittlere molare thermische Energie pro Freiheitsgrad steigt mit zunehmender
R⋅T Temperatur an: E = (1)
therm 2
Suche: Wie sind für einen Freiheitgrad die einzelnen
Energieniveaus besetzt.
Konkret: Wie sieht die Verteilung der kinetische Energie
(und somit der Geschwindigkeiten) der
Gasmoleküle in Abhängigkeit von der
Temperatur T aus ?
Energieniveaus Ei
Besetzungszahl Ni.
Bedingungen: Wir suchen eine Energieverteilung, die
folgende Bedingungen erfüllt:
1. Die Gesamtzahl der Moleküle ist N:
N=∑ Ni(Teilchenzahlerhaltung)
(2)
i
2. Eges = ∑ Ni⋅Ei(Energieerhaltung) (3)
i
Ni
gleichbedeutend mit: E = ∑ ⋅Ei(4)
i N
Einfaches Beispiel:
Es seien 6 Energiezustände mit Energie E0=0, E1=1,E2=2 ect. gegeben
Die Zahl der Teilchen ist N=3
Die mittlere Energie pro Teilchen sei 1, d.h. die Gesamtenergie sei Egesamt=5
Frage: Welche Möglichkeiten gibt es die 3 Teilchen auf die 6 Zustände zu verteilen, so dass
die Gesamtenergie konstant bleibt? Wie häufig ist dann jeder einzelne Zustand besetzt?
j
1
2
3
4
5
N
i
=
i 1 2 3 4 5 6
E 0 1 2 3 4 5 Eges W
∑
n ⋅W
•• • 5
• • • 5
• • • 5
•• • 5
• •• 5
j
j
∑ Wj
j
j
6/7 5/7 4/7 2/7 1/7 3/7 ∑
i
i 3
N = = N
WS2007 PC1/ Dr. Ogrodnik 1 Boltzmannverteilung
∑
j
3
6
6
3
3
W = 21
j
nj=2

INFOBOX: Wahrscheinlichkeitsrechnung (Kombinatorik):
Wieviele Realisierungsmöglichkeiten W gibt es, jeweils die drei unterscheidbaren
Teilchen auf N Zellen einer Zeile (Zeilenummer j) der obigen Tabelle zu verteilen?
2. Zeile (j=2): Die möglichen Reihenfolgen mit der drei Teilchen angeordenet werden
kann=Zahl der Permutationen = 3!
Analog ist die 3. Zeile zu behandeln
1. Zeile (j=1): Es gibt drei Möglichkeiten die drei Moleküle anzuordnen
(die Reihenfolge innerhalb einer Zelle spielt keine Rolle, denn es kommt nur auf die
Tatsache an, dass das eine oder andere Teilchen eine bestimmte Energie hat, nicht aber in
welcher Reihenfolge wir die Teilchen gleicher Energie notiert haben )
Zahl aller Permutationsmöglichkeiten N !
=
Zahl Permutationsmöglichkeiten n ! innerhalb jeder Zelle n !
n1!=2!=2 n3!=0!=1 n5!=1!=1
Analog Zeile 4 und 5.
i
3x2=6 Möglichkeiten
= Zahl der
Permutationsmöglichkeiten
W2=N!
Um die gesamte Verteilung zu erhalten, muss man nun "lediglich" die Zahl der Teilchen in
den Zellen der ersten Spalte jeweils mit der Zahl der Realisierungsmöglichkeiten Wj
multiplizieren und zusammenaddieren, dann die Zahl aller Teilchen in der 2. Spalte mit Wi
gewichten und so fort.
WS2007 PC1/ Dr. Ogrodnik 2 Boltzmannverteilung
∑
i
i
3 Möglichkeiten
N !
W1
=
n ! ⋅n ! ⋅n
!:.... ⋅n
!
=
1
N !
n !
∏
i
i
2 3
3! 6
= = = 3
2!0!0!0!0!1 ⋅ ⋅ ⋅ ⋅ ! 2
m

Für obiges Beispiel erhalten wir:
1. Spalte (Energie 0): 2. Spalte (Energie 1):
2⋅ W = 2⋅ 3
1
1⋅ W = 6
2
1⋅ W = 6
0
0
∑
2
= 6+ 6+ 6+ 0+ 0= 18
Diese Besetzungswahrscheinlichkeit kann noch auf die Gesamtzahl der
Realisationsmöglichkeiten ∑ Wj
normiert werden und ist in der letzten Zeile
j
0
1⋅ W = 6
zusammengetragen.
Wir bekommen folgende Besetzungswahrscheinlichkeit als Funktion der Energie:
Suche nach der am häufigsten vorkommenden Anordnung
Natürlich ist die Statistik dieser Verteilung von nur 3 Teilchen noch sehr schlecht. Bei einer
sehr großen Zahl von Teilchen (10 23 !) wird diese extrem genau. Andererseits ist es nicht
möglich, wie oben, alle denkbaren Kombinationen durchzuspielen.
Ansatz: Da hilft uns folgende Überlegung weiter: Es gibt viele Anordnungsmuster, die sich
sehr ähnlich sind und sehr häufig vorkommen (viele Permutationsmöglichkeiten haben).
Als Gegenbeispiel betrachten wir den extrem unwahrscheinlichen Fall, dass ein Teilchen die
gesamte Energie trägt, und alle anderen 10 23 Teilchen keine kinetische Energie haben (erste
Zeile in der Tabelle: ein Teilchen ist im letzten rechten Kasten, alle anderen sind im ersten
N !
linken Kasten). Für diesen Fall ist W1= = N
( N −1!
)
Der andere Extremfall wäre wenn jeder Zustand nur einfach besetzt wäre. Da gilt: W2 = N!
WS2007 PC1/ Dr. Ogrodnik 3 Boltzmannverteilung
2
0
2⋅ W = 2⋅ 3
1
1⋅ W = 6
∑
2
= 0+ 6+ 0+ 6+ 6= 18

W N !
= = − 1! wahrscheinlicher!!!
W1N Gehen wir vom zweiten Fall aus und besetzen nur eine Zelle doppelt, so erhalten wir:
N !
W 3=
2!
2
Der zweite Fall wäre um den Faktor ( N )
Suche nach dem maximalen W
Es stellt sich heraus, dass es bei sehr großen Zahlen genügt, das Verteilungsmuster mit den
meisten Permutation zu finden, ( das wäre die am häufigsten vorkommende Zeile in obiger
Tabelle). Sie ist representativ für die gesamte Verteilung (die übrigen Verteilungsmuster sind
entweder sehr ähnlich, und damit ebenfalls sehr häufig, oder unterschieden sich signifikant
und kommen dann sehr selten vor, und tragen zur Verteilung praktisch nicht bei).
Wir wollen also die Anordnung finden, für die Zahl der Permutationsmöglichkeiten W
maximal wird.
N !
Wir gehen aus von: W =
∏ Ni
!
i
(5).
Bei den großen Werten von N und Ni mit denen wir es zu tun haben, ist es nützlich den
Logarithmus von (5) zu nehmen, und davon das Maximum zu suchen:
⎛ ⎞
ln( W) = ln( N!) − ln ⎜∏ Ni! ⎟=
ln( N!) −∑ln
( Ni!
) (6)
⎝ i ⎠
i
Das maximale W bzw. das maximale ln(W) finden wir, wenn die Ableitung von W nach einer
kleinern Veränderung der Verteilung gleich Null wird. Da ln(W) eine Funktion vieler
Variabler Ni ist betrachten wir das vollständige Differenzial
( W) ( W)
∂ln d ln ( W ) =
∂N1 ∂ln
⋅ dN1+ ∂N2
⋅ dN2+
....... und setzen dies gleich Null.
∂ ln( N !) ⎛∂ln( N !) ⎞!
i
Aus (6) erhalten wir somit: d ln( W ) = dN + ∑⎜
⋅ dNi
⎟=
0 (7)
∂N i ⎝ ∂Ni⎠
dN=
0
da N konst.!
Mit der Stirling´schen Formel ln( x!) ≈x⋅ln( x) − x (für große x) können wir uns der
mathematisch unhandlichen Fakultäten entledigen und erhalten für (7):
∂{ Ni⋅ln( Ni) −Ni}
dln( W) = ∑ ⋅ dNi=
0 (8)
i ∂Ni
Wir können nun die einzelnen Therme der Summe in (8) ableiten:
⎡∂{ Ni⋅ln( Ni) } ∂{
Ni}
⎤ ⎧
⎢ − ⎥dNi=
⎨ln( Ni) ⎣ ∂Ni ∂Ni ⎦ ⎩
∂N ln( ) 1
i ∂ Ni
⋅ ln( Ni) + Ni⋅
∂Ni ∂Ni
1
Ni
und erhalten somit für (8):
∑ ln( Ni) ⋅ dNi=
0 (10)
i
1 ⎫
+ Ni⋅ −1⎬dNi
(9)
Ni
⎭
0
Wir können nun auch die Bedingung 1 und 2 in differentieller Form fassen:
WS2007 PC1/ Dr. Ogrodnik 4 Boltzmannverteilung

Die Teilchenzahlerhaltung (2) N = ∑ Ni = konst!
ist gleichbedeutend mit: 0
i
∑ dN i = 0 (11)
i
∑ ⇒ dE = 0⇒
Ebenso die Energieerhaltung: (3) E = N ⋅ E = konst!
ges i i
i
(Beachte: da die Zustandsenergien fest sind dE i = 0)⇒
∑ dNi⋅ Ei=
0 (12)
i
dN = ⇒
Es müssen nun alle drei Bedingungen (10), (11) und (12) gleichzeitig erfüllt werden.
„Methode der unbestimmten Lagrange´schen Multiplikatoren“
Mit dieser Methode kann die gleichzeitige Erfüllung von mehreren unabhängigen
Bedingungen mathematisch gewährleistet werden. Nach dieser Methode werden obige
Zusatzbedingungen (10) und (11) mit vorerst unbekannten Faktor α bzw. β (das sind die
Lagrange´schen Multiplikatoren) multipliziert und anschließend zu Bedingung (12) addiert:
α⋅ 0+ β⋅ 0+ 0= α⋅ dN + β⋅
dN ⋅ E + ln( N ) ⋅ dN = 0
∑ ∑ ∑ oder:
i i i i i
i i i
∑ { α+ β⋅ Ei+ ln( Ni) } ⋅ δNi=
0 (13)
i
Einschub: Zum „Beweis“ sei hier ein einfaches Beispiel gerechnet:
Ges.: Welches Rechteck ergibt bei konstant gehaltenem Umfang die größte Fläche?
Ansatz: Fläche: A= xy ⋅ (14)
Umfang: U= 2x+ 2y
(15)
Wir suchen das Maximum von A ⇒ δ A= x⋅ δ y+ y⋅ δx=
0 (16)
Umfang konstant ⇒ δU= 2δx+ 2δ y=
0 (17)
Mit dem unbestimmten Multiplikator α fassen wir (16) und (17) zusammen:
δA+ α⋅ δU= x⋅ δ y+ y⋅ δx+ α⋅ 2δx+ 2δ y = 0
( )
δx und δy Terme zusammengefasst: ( ) ( )
y+ 2α ⋅ δx+ x+ 2α δ y=
0 (18)
Wir betrachten x und y als Größen die unabhängig voneinander variiert werden.
Dann ist (18) nur dann erfüllt, wenn beide Terme unabhängig Null sind, d.h. wenn
( y+ 2α) = 0 und ( x+ 2α) = 0.
Daraus folgt unmittelbar: x=y.
Ergebnis: Ein Quadrat hat bei vorgegebenem Umfang die größte Fläche.
Auf Gleichung (13) angewandt bedeutet dies, dass jeder der Summenterme unabhängig Null
sein muss:
α + β ⋅ Ei+ ln( Ni)
für alle Werte von i.
Nach Ni aufgelöst erhält man:
Ei
Nie e β α − ⋅ −
= ⋅ (19)
Ni
Man kann nun (19) in (4): E = ∑ ⋅Eieinsetzen
und die mittlere Energie berechnen, die
i N
R⋅T 1
laut Gl. (1) ergeben muss. Daraus folgt, dass β = (20)
2
R⋅T WS2007 PC1/ Dr. Ogrodnik 5 Boltzmannverteilung
ges

Betrachten wir nur das Verhältnis der Besetzungszahlen zweier Energieniveaus Ei und Ei, so
kürzt sich der konstante Faktor e -α heraus und man erhält:
( Ei−Ej) N −
i RT ⋅ = e (21) Boltzmannfaktor
N
j
Der Boltzmannfaktor ist ein zentrales Ergebnis der statistischen Thermodynamik und wurde
anhand von puren statistischen Überlegungen abgeleitet.
Der Boltzmannfaktor gibt das Verhältnis der Besetzungswahrscheinlichkeiten zweier
Zustände unterschiedlicher Energie an. Ist Ei>Ej (der Zustand i liegt oberhalb von j), dann ist
der Quotient Ni/Nj < 1, d.h. der höher gelegene Zustand ist weniger stark besetzt als der
energetisch tiefere.
Fall: T→0: der Exponent geht → -∞, d.h. die e - Funktion geht gegen 0, d.h. der unteres
Zustand ist ausschließlich besetzt.
Fall: T→∞: der Exponent geht → 0, d.h. die e - Funktion geht gegen 1, d.h. beide Zustände
sind im Grenzfall maximal gleich besetzt.
Beachte: Ni ist immer kleiner als Nj. Es gibt im thermischen Gleichgewicht keine sogenannte
Besetzungszahlinversion (Ni>Nj). Diese benötigt man z.B. um Laseremission zu erzielen.
Die gesamte Verteilungsfunktion ergibt sich, wenn man den Boltzmannfaktor auf die Summe
aller Besetzungszahlen normiert:
Ei
−
RT ⋅ Ni e
i = = E j ∑ N j
−
RT ⋅
j ∑e
j
f
Boltzmannverteilung
Die Zustandssumme: Der Summenterm im Nenner heißt die molekulare Zustandssumme.
Sie gibt an wie viele Zustände insgesamt bei einer bestimmten Temperatur für ein Molekül
thermisch zugänglich sind. Um sie berechnen zu können muss man die Energien Ej aller
Zustände kennen. Die statistische Mechanik beschäftigt sich damit, wie man diese
Zustandssumme für die verschiedenen Freiheitsgrade berechnen kann. Ist die Zustandssumme
einmal ermittelt, dann lassen sich aus ihr alle thermodynamischen Funktionen einfach
berechnen.
WS2007 PC1/ Dr. Ogrodnik 6 Boltzmannverteilung