Kraftgrößenverfahren

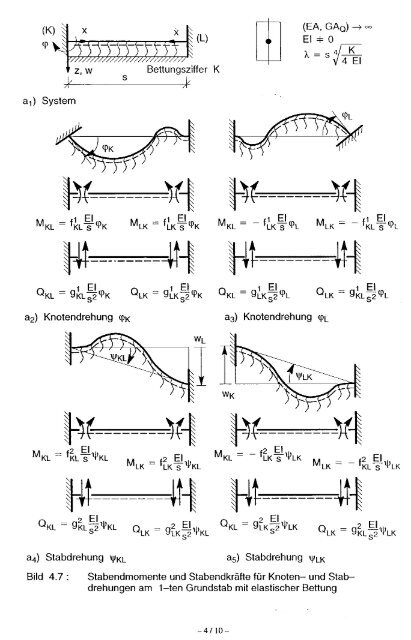
Stabendmomente nach Theorie I. Ordnung für das Drehwinkelverfahren
Grundstab 1
Belastung+Biegelinie Stabendmomente Momentenverlauf
Knotenverdrehung φ K
M
EI
4
s
KL
φ K
EI
MLK
-2 φ
s
K
Knotenverdrehung φ L
EI
M 2
s
KL
φ L
EI
MLK
- 4 φ
s
L
Stabverdrehung ψ KL
EI
s
M
EI
6 ψ
s
MKL
-6 ψKL
LK
KL
Stabverdrehung ψ LK
EI
s
EI
s
MKL -6 ψ LK
MLK
6 ψ
LK
ps²
ps²
Streckenlast
M KL
- M LK
-
12
12
Temperaturdifferenz
M
KL
α
-EI
T
ΔT
h
h
M
LK
α
-EI
T
ΔT
h
h
Einzellast
M KL
-Fsαβ²
M LK
-Fsαβ²
Einzelmoment
M KL
M 2β 3β²
M LK
M 2α 3α²

Stabendmomente nach Theorie I. Ordnung für das Drehwinkelverfahren
Grundstab 2
Belastung+Biegelinie Stabendmomente Momentenverlauf
Knotenverdrehung φ K
M
EI
3
s
KL
φ K
Knotenverdrehung φ L
M
LK
EI
- 3
s
φ
L
Stabverdrehung ψ KL
M
EI
- 3
s
KL
ψ KL
Stabverdrehung ψ LK
M
EI
3
s
LK
ψ LK
Streckenlast
M KL
ps²
-
8
Temperaturdifferenz
M
KL
- 1.5 EI
αTΔTh
h
Einzellast
M KL
1 1
Fsα
β
β ²
2 2
Einzelmome nt
M KL
1 3
M
β ²
2 2

Berechnung von Einflusslinien für Kraftgrößen an
statisch unbestimmten Systemen mit dem
Kraftgrößenverfahren
Berechnung der Einflusslinien für statisch Überzählige
(vgl. Buch Tragwerke 2)
Die Berechnung der Einflusslinie kann für jede beliebige statisch Überzählige X j des
gewählten SGS erfolgen.
Satz: Die Einflusslinie n X km einer statisch Überzähligen entsteht als Biegelinie des
Lastgurtes infolge der Kraftgrößeneinwirkung X j = 0 β kj (j = a, b, .., i, ..n).
Die Einflusslinie ergibt sich aus der Überlagerung der Einflusslinien der einzelnen
Zustände der statisch Überzähligen.
X j
statisch Überzählige
k Ort der gesuchten Einflussgröße
n Grad der statischen Unbestimmtheit
0 β kj Elemente der Matrix 0 β
Matrix 0 β negative Inverse der Matrix 0 δ
Berechnungsverfahren: Für eine Einflusslinie einer Kraftgröße an der Stelle k
1. Wahl eines SGS, das die gesuchte(n) Einflussgröße(n) als statisch
Überzählige besitzt
2. Berechnung der Matrix 0 δ
3. Berechnung der Matrix 0 β = - ( 0 δ -1 )
Es sind 2 verschiedene Wege möglich, um die Einflusslinie zu bestimmen. Der
Zeitpunkt der Superposition unterscheidet beide Algorithmen.
Lösungsweg A
4.A Ermittlung der n Biegelinien (jedes
Einheitszustandes) infolge X j = 1
(Biegelinie entspricht der EL)
5.A Superposition der Biegelinien der
Einzelzustände
n X km = 0 β k1 * 0 δ m1 + 0 β k2 * 0 δ m2 + …+ 0 β kn * 0 δ mn
Lösungsweg B
4.B Belastung des SGS mit
X 1 = 0 β k1 , X 2 = 0 β k2 ,… X n = 0 β kn
(Superposition der Belastung)
5.B Berechnung der Biegelinie
(Biegelinie entspricht der EL)
Diese Methode eignet sich vorrangig für die Bestimmung verschiedener Einflusslinien
eines Systems.
1

Alternative:
Berechnung von Einflusslinien gemäß dem Satz von Land
Satz von Land:
Die Einflusslinie für eine Kraftgröße an der Stelle k entsteht als Biegelinie des
Lastgurtes, wenn man am Ort k der gesuchten Einflusslinie die Kraftgröße durch ein
Gelenk aus der kraftschlüssigen Bindung befreit und im Gelenk die zur Kraftgröße
arbeitskonforme Weggröße „-1“ einprägt.
Die Berechnung der Einflusslinie ist als Lastfall eingeprägter Weggrößen
(Wegsprung) zu betrachten.
vgl. Arbeitsblatt: Berechnung statisch unbestimmter Systeme unter der Einwirkung
von eingeprägten Weggrößen
Der Berechnungsgang wird maßgeblich von der Wahl des SGS bestimmt.
1. Variante: Kombinierte Gelenkmethode
Eine der statisch Überzähligen X i im SGS entspricht der gesuchten Einflussgröße. An
dieser Stelle wird gemäß des Satzes von Land der arbeitskonforme Wegsprung von
„-1“ eingeführt.
am Ort der gesuchten Einflussgröße δ i = −1
für alle andere „Gelenke“ gilt der Gelenkschluss d. h. δ i = 0
δ 10 , δ 20 , .. δ i0 = 0
2. Variante: Getrennte Gelenkmethode
Das SGS wird so gewählt, dass keine der statisch Überzähligen der gesuchten
Einflussgröße entspricht.
für alle eingeführten Gelenke gilt der Gelenkschluss, d.h. δ i = 0
die Größen δ 10 , δ 20 , .. δ i0 sind zu bestimmen
Die Ermittlung der Größen δ 10 , δ 20 , .. δ i0 kann erfolgen mit
a) PVK
z. B. Einflusslinie der Querkraft im Punkt k, gemäß Satz von Land ist an der
Stelle k der Wegsprung von „-1“ als Belastung einzuprägen, n = 2-fach
statisch unbestimmt δ 20
δ 1 Q k
* ∆w
0 δ 1 Q *( −1)
0
20
* +
2 k 0
=
b) Polplan
20
* + k 2
=
Nach Lösung des Gleichungssystems und Superposition der Lösung wird die
Biegelinie ermittelt (PVK mit Reduktionssatz, ω-Verfahren, etc.).
2

Ermittlung der geometr. Unbestimmheit
1. System gedanklich in einzelne Staäbe unterteilen, die durch Auflager oder
Geometriesprünge begrenzt werden.
(1)
(2)
(3)
2.
Anordnen von Drehfesseln an den markanten Punkten, an denen weder die Verdrehung
noch das Moment bekannt ist.
2 Drehfesseln
3. Prüfen am Gelenkwerk (Momentengelenke an den markanten Punkten bzw. Stabendpunkten
einfügen), ob dann das System verschieblich ist und ggf. durch Anordnen von Wegfesseln
unverschieblich machen.
B2S
B2S
B2S
beachte: EA
∞
1 Wegfessel erforderlich
(unterschiedliche Anordnung
möglich)
B2S
3GR
4.
Der Grad der geometr. Unbestimmheit ergibt sich als die Summe aller Fesseln.
3 fach geometr.
unbestimmt

Kraftgrößenverfahren (KGV)
1. Bestimmung des Grades der statischen Unbestimmtheit
Abzählkriterium, Aufbauprinzip
2. Wahl eines statisch bestimmten Grundsystems (SGS) / Hauptsystems
(HS) und Festlegung der statisch Überzähligen X i , i=1,...,n
kein kinematisch verschiebliches System oder Teilsystem entwickeln
möglichst wenig gemeinsame „Momentenflächen“ einzelner Zustände,
Ziel: geringer Aufwand beim PVK
3. Ermittlung der Schnitt- und Auflagergrößen der Lastzustände am
SGS/HS
N XL , Q XL , M XL , … N XV , Q XV , M XV „0“-Zustand: „N 0 “, „Q 0 “und „M 0 “
4. Ermittlung der Schnitt- und Auflagergrößen der n Einheitszustände am
SGS/HS
X i =1: N xi, Q xi , M xi
„1“, „2“, …, „n“-Zustände: z. B.: „N 1 “, „Q 1 “und „M 1 “ etc.
5. Bestimmung aller Klaffungen (Gelenkverformungen) der Lastzustände
sowie der n Einszustände mit dem PVK
L
N
xk
QxiQxk
M
xk ΔT
1⋅δ ik
= ∫{
N
xi[
+ αTT]
+ + M
xi[
+ αT
]} dx +
EA GA EI h
−
∑
L
C
Li
0
⋅c
Lk
−
∑
w
M
wi
ϕ
wk
Q
∑
n
N
ni
c
N
n
nk
+
∑
m
M
mi
c
M
m
mk
6. Aufbau und Lösung des Systems der Elastizitätsgleichungen
δ = δ
i
i0
+ X
⇒ Beispiel
1
* δ
11
+ ... + X
n
* δ
in
= 0
Cramersche Regel:
Ist A eine quadratische (n,n)-Matrix mit | A | ≠ 0, so ist
δ = δ
1
2
⎡δ
⎢
⎣δ
11
21
10
δ = δ
20
+ X
1
+ X
1
* δ
1
2
11
* δ
δ12
⎤ ⎡ X
⎥ *
δ
⎢
22 ⎦ ⎣X
21
+ X
2
+ X
2
* δ
12
* δ
22
⎤ ⎡−
δ10
⎤
⎥ = ⎢ ⎥
⎦ ⎣−
δ
20 ⎦
= 0
= 0
das LGS A * x r = b r eindeutig lösbar. Für die Lösungen
x r = (x 1 , x 2 , … , x n ) gilt:
x i = | A i | / | A | , für i = 1, 2, … , n
wobei A i die (n,n)-Matrix ist, die aus A entsteht, indem
r
man die i-te Spalte von A durch b ersetzt.
7. Ermittlung der wirklichen Schnitt- und Auflagergrößen durch
Superposition
z. B. M ges = M 0 + X 1 *M 1 + ….. + X n *M n

Berechnung statisch unbestimmter Systeme unter der
Einwirkung von eingeprägten Weggrößen
Beispiele:
- Auflagerverdrehung ∆ φ
- Stützensenkung u z , u x
- Winkelsprung ∆φ
- Verschiebungssprung ∆ u z , ∆ u x
Es gilt die Polplankinematik, d. h. eingeprägte Weggrößen bewirken keine
Schnittgrößen am statisch bestimmten System. Statisch bestimmte Systeme sind in
der Lage sich zwangsfrei zu verformen.
Erfassung des Lastfalls „eingeprägte Verschiebung“ im Kraftgrößenverfahren
Der Berechnungsgang wird maßgeblich von der Wahl des SGS bestimmt.
1. Variante:
Einführung der statisch unbestimmten Größen X i als arbeitskonforme Größe zur
eingeprägten Weggröße.
δ 10 , δ 20 , .. δ i0 = 0
aber δ i = δ an Orten eingeprägter Verschiebungen δ arbeitskonform zur Unbekannten
X i bzw. δ i = 0 sonst
2. Variante:
Das SGS wird so gewählt, dass keine der statisch Unbestimmten arbeitskonform zu
eingeprägten Verschiebungsgrößen wirkt.
δ i = 0
Die Ermittlung der Größen δ 10 , δ 20 , .. δ i0 kann erfolgen mit
a) PVK
b) Polplan

Ausnutzung der Symmetrieeigenschaften des Systems
Berechnung am halben System
Gruppenlasten
1. Berechnung am halben System
Vorraussetzung:
Es muss ein symmetrisches System vorliegen, dass entweder eine symmetrische
oder antimetrische Belastung aufweist. Eine beliebige Belastung kann mittels einer
Belastungsumordnung (BU-Verfahren) in symmetrische und antimetrische
Lastanteile aufgeteilt werden.
Gemäß der vorliegenden Belastungsform (symmetrisch oder antimetrisch) wird das
das halbe System mit den entsprechenden Randbedingungen in der
Symmetrieachse entwickelt. Die Berechung erfolgt am halben System.
Für die Berechnung am halben System wird auf das Arbeitsblatt „Symmetrie“
verwiesen.
2. Berechnung mittels Gruppenlasten
Bei der Berechnung symmetrischer Tragwerke nach dem Kraftgrößenverfahren mit
Gruppenlasten bleibt die Anzahl der Unbekannten n stets erhalten.
Es gilt: n = n symm + n anti
Ferner gilt für die Anzahl der Unbekannten der symmetrischen und antimetrischen
Zustände:
Kraftgrößenverfahren
Symmetrie Antimetrie
n n
n symm
≥ n anti
≤
2 2
Vorgehensweise mit Gruppenlasten:
1. SGS muss symmetrisch sein
2. Anzahl der Gruppenzustände == Grad der statischen Unbestimmtheit
3. Gruppen so wählen, dass sie paarweise (2 Kraftgrößen) symmetrisch bzw.
antimetrisch sind
4. das Einfügen eines Gelenks (statisch Überzählige) in der Symmetrieachse
bildet mit dieser Kraftgröße einen Gruppenzustand, der entweder symmetrisch
oder antimetrisch ist
5. Die Überlagerung von symmetrischen und antimetrischen Zuständen ergibt Null

3. Gegenüberstellung der Verfahren
Berechnung am halben System
Vorteile:
Bei antimetrischer Belastung kann die
statische Unbestimmtheit entschieden
verringert sein
Berechnung mittels Gruppenlasten
Nachteil:
Das Verfahren ist weniger anschaulich.
Nachteile:
Die Belastung muss entweder
symmetrisch oder antimetrisch sein,
um die Symmetriebedingungen
anwenden zu können.
Eine Zerlegung einer beliebigen Last in
symmetrischen und antimetrischen
Anteil nach dem
Belastungsumordnungsverfahren ist
möglich. Jedoch gehen die Vorteile
aufgrund dieser Berechnung aufgrund
eines symmetrischen und
antimetrischen Berechnungsgang
verloren.
Vorteil:
Die Belastung muss nicht symmetrisch
sein.
Durch eine Entkopplung der
symmetrischen und antimetrischen
Einheitszustände wird das
Gleichungssystem vereinfacht. Dieses
Verfahren ist auch auf unsymmetrische
begrenzt anwendbar.