Lehrveranstaltung Statik der Baukonstruktionen IV - Fachgebiet ...

Technische Universität Berlin
Fachgebiet Statik der Baukonstruktionen
Prof. Dr.–Ing. Rudolf Harbord
Lehrveranstaltung
Statik der Baukonstruktionen IV
– Flächentragwerke –
Berlin ⋅ März 2003

Inhaltsverzeichnis Seite
Literatur 5
Teil 1: Flächentragwerke
1.1 Einführung 1 / 1
1.2 Begleitende Literatur 1 / 4
1.3 Statische Modelle 1 / 5
1.4 Vorgehensweisen und Berechnung 1 / 7
1.5 Anwendungsbeispiele 1 / 10
1.5.1 Wandscheibe 1 / 11
1.5.2 Flach– und Pilzdecke 1 / 17
1.5.3 Behälter 1 / 23
1.5.4 Faltwerk 1 / 30
1.6 Erkenntnisse 1 / 35
Teil 2: Bezeichnungen
2.1 Indexschreibweise 2 / 1
2.2 Geometrische Größen 2 / 3
2.3 Einwirkungsgrößen 2 / 4
2.4 Zustandsgrößen 2 / 5
2.5 Arbeitskonforme Größen 2 / 6
Teil 3: Scheibentheorie
3.1 Einführung 3 / 1
3.2 Voraussetzungen der Scheibentheorie 3 / 1
3.3 Berechnungsgrößen der Scheibentheorie 3 / 3
3.4 Grundgleichungen der Scheibentheorie 3 / 5
3.4.1 Gleichgewicht 3 / 5
3.4.2 Verträglichkeit 3 / 7
3.4.2.1 Kinematischer Verzerrungszustand 3 / 7
3.4.2.2 Materieller Verzerrungszustand 3 / 9
3.4.2.3 Berechnungsgleichungen 3 / 12
– 1 –

– 2 –
Seite
3.4.3 Bilanz 3 / 13
3.4.4 Randbedingungen 3 / 13
3.5 Lösungswege der Scheibentheorie 3 / 16
3.5.1 Gemischte Formulierung in Weg– und Kraftgrößen 3 / 16
3.5.2 Gleichgewichtsformulierung in Weggrößen 3 / 17
3.5.3 Verträglichkeitsformulierung in Kraftgrößen 3 / 18
3.6 Lösungsmethoden der Scheibentheorie 3 / 20
3.7 Beispiel zum Verfahren von Schleeh 3 / 23
Teil 4: Plattentheorie
4.1 Einführung 4 / 1
4.2 Voraussetzungen der Plattentheorie 4 / 1
4.3 Berechnungsgrößen der Plattentheorie 4 / 2
4.4 Grundgleichungen der Plattentheorie 4 / 4
4.4.1 Gleichgewicht 4 / 4
4.4.2 Verträglichkeit 4 / 6
4.4.2.1 Kinematischer Verzerrungszustand 4 / 7
4.4.2.2 Materieller Verzerrungszustand 4 / 9
4.4.2.3 Berechnungsgleichungen 4 / 12
4.4.3 Bilanz 4 / 13
4.4.4 Randbedingungen 4 / 13
4.5 Lösungswege der Plattentheorie 4 / 18
4.6 Lösungsmethoden der Plattentheorie 4 / 19
4.6.1 Analytische Integration der Plattengleichung 4 / 19
4.6.2 Ritz–Verfahren 4 / 25
4.7 Beispiel zum Ritz–Verfahren 4 / 28

Teil 5: Schalentheorie
– 3 –
Seite
5.1 Einführung 5 / 1
5.2 Technische Schalenformen 5 / 8
5.2.1 Einfluß der Schalenform 5 / 8
5.2.2 Klassifikation von technischen Schalenformen 5 / 10
5.2.3 Anwendungen im konstruktiven Ingenieurbau 5 / 14
5.3 Zur baustatischen Berechnung von Rotationsschalen 5 / 18
5.3.1 Allgemeines 5 / 18
5.3.2 Membranlösung 5 / 19
5.3.3 Biegelösung 5 / 24
5.3.4 Beispiel Wasserbehälter 5 / 30
5.4 Membrantheorie von Allgemeinen Schalen 5 / 38
5.4.1 Kräftegleichgewicht 5 / 39
5.4.2 Kovariante Ableitung und Krümmung 5 / 40
5.4.3 Rotationsschalen 5 / 45
Teil 6: Gitterrostmethode (GRM)
5.4.3.1 Allgemeine Rotationsschalen 5 / 45
5.4.3.2 Kugelschale 5 / 48
5.4.3.3 Lastfall Innendruck einer Vollkugel 5 / 53
6.1 Baustatischer Lösungsansatz mit Gitterrosten 6 / 1
6.2 Scheibe und Fachwerk 6 / 2
6.2.1 Einleitung 6 / 2
6.2.2 Querschnittsflächen der Gitterroststäbe 6 / 4
6.2.3 Scheibenbeispiel Kragarm: Verschiebungen 6 / 18
6.2.4 Ermittlung der Scheibenkräfte 6 / 22
6.2.5 Scheibenbeispiel Kragarm: Spannungen 6 / 37
6.2.6 Stab–Querschnittsflächen für beliebige Querdehn–
zahlen 6 / 42

– 4 –
Seite
6.3 Platte und Rahmenwerk 6 / 48
6.3.1 Einleitung 6 / 48
6.3.2 Trägheitsmomente der Gitterroststäbe 6 / 50
6.3.3 Beispiel: Konvergenzverhalten von Platten–
Gitterrostelementen 6 / 52
6.3.3.1 Quadratische Platte 6 / 52
6.3.3.2 Rechteckige Platte 6 / 57
6.4 Hinweise zur Benutzung von Programmen 6 / 61
6.4.1 Allgemeines 6 / 61
6.4.2 Genauigkeit 6 / 61
6.4.3 Berechnung einer Aussteifungsschale 6 / 64
Teil 7: Finite–Element–Methode (FEM)
7.1 Einführung 7 / 1
7.2 Geometrische Definition von finiten Elementen auf Flächen 7 / 2
7.3 Topologie von finiten Elementen auf Flächen 7 / 3
7.4 Finite Plattenelemente 7 / 6
7.4.1 Geometrie und Ansätze 7 / 6
7.4.2 Diskretisierung auf Element– und Systemebene 7 /11
7.4.3 Überprüfung der Konvergenz 7 /12
7.4.4 Einfaches Anwendungsbeispiel 7 /14
7.5 Finite Scheibenelemente 7 /18
7.5.1 Geometrie und Ansätze 7 /18
7.5.2 Diskretisierung 7 /20
7.5.3 Überprüfung der Konvergenz 7 /21
7.5.4 Anwendungsbeispiel 7 /23

Literatur
/ 1 / Girkmann, K.: Flächentragwerke, sechste Auflage.
Springer–Verlag (1963).
/ 2 / Flügge, W.: Statik und Dynamik der Schalen, dritte Auflage.
Springer–Verlag (1962).
/ 3 / Mang, H.: Flächentragwerke. Beitrag in: Der Ingenieurbau,
Rechnerorientierte Baumechanik, S. 1–139.
Verlag Ernst & Sohn (1995).
/ 4 / Basar, Y., Krätzig, W. B.: Mechanik der Flächentragwerke.
Vieweg–Verlag (1985).
/ 5 / Eschenauer, H., Schnell, W.: Elastizitätstheorie I (Grundlagen, Scheiben und
Platten) und II (Schalen).
BI–Wissenschaftsverlag (1981).
/ 6 / Schleeh, W.: Bauteile mit zweiachsigem Spannungszustand
(Scheiben).
Beton–Kalender II (1983), S. 713–848.
/ 7 / Pieper, K., Martens, P.: Durchlaufende vierseitig gestützte Platten im
Hochbau. Vorschlag zur vereinfachten Berech–
nung.
Beton– und Stahlbetonbau (1966), S. 158–162.
/ 8 / Markus, G.: Theorie und Berechnung rotationssymmetrischer
Bauwerke, zweite Auflage.
Werner–Verlag (1976).
/ 9 / Grasser, E., Thielen, G.: Hilfsmittel zur Berechnung der Schnittgrößen und
Formänderungen von Stahlbetontragwerken.
2. überarbeitete Auflage. Deutscher Ausschuß für
Stahlbeton (DAfStb), Heft 240,
Beuth Verlag (1978).
/10/ Zimmer, A., Groth, P.: Elementmethode der Elastostatik.
R. Oldenburg–Verlag (1970).
/11/ Knothe, K, Wessels, H.: Finite Elemente.
Springer–Verlag (1991).
/12/ Harbord, R.: Statik der Baukonstruktionen III
– Rechnerorientierte und nichtlineare Statik von
Stabtragwerken. Manuskript zur Lehrveranstal–
tung, TU Berlin (1996).
/13/ Harbord, R.: Statik der Baukonstruktionen, Vertiefung I:
Finite–Elemente–Methoden in der Baustatik und
Baudynamik. Manuskript zur Lehrveranstaltung,
TU Berlin (1997).
– 5 –

14/ Isler, H.: Schalen. Katalog.
Hrsg.: E. Ramm, E. Schunk, Universität Stuttgart.
Karl Krämer Verlag, Stuttgart (1989).
/15/ Straub, H.: Die Geschichte der Bauingenieurkunst.
Birkhäuser Verlag (1992).
/16/ Pflüger, A.: Elementare Schalenstatik, fünfte Auflage.
Springer–Verlag (1981).
/17/ Franz, G.: Konstruktionslehre des Stahlbetons.
Zweiter Band: Tragwerke.
Springer–Verlag (1969).
/18/ Bomhard, H., Kraemer, U.,
Mainz, J.: Wiederaufbau der Kongreßhalle Berlin
– Konstruktion und Bau.
Bauingenieur 61 (1986), S. 569–576.
/19/ Schlaich, J., Schober, H.: Netzkuppeln aus Glas.
VDI–Jahrbuch (1994), S. 238–260.
/20/ Czerny, F.: Tafeln für Rechteckplatten.
Beton–Kalender I (1996), S. 277.
/21/ Stiglat, K., Wippel, H.: Massive Platten.
Beton–Kalender I (1997), Seite 283.
/22/ Werkle, H.: Finite Elemente in der Baustatik.
Vieweg–Verlag (1995).
/23/ Krätzig, W.B., Basar, Y.: Tragwerke 3. Theorie und Anwendung der
Methode der finiten Elemente.
Springer–Verlag (1997).
– 6 –

Teil 1: Flächentragwerke
1.1 Einführung
Die Lehrveranstaltung Statik der Baukonstruktionen IV – kurz Statik IV – ist zwischen
Grundfach– und Vertiefungsstudium angeordnet. Sie richtet sich an Studentinnen und
Studenten, die bereits die Lehrveranstaltungen Statik I bis III des Grundfachstudiums
erfolgreich abgeschlossen haben und die anstreben, sich verstärkt in eine statisch–konstruktive
Richtung zu vertiefen.
Ziel der Veranstaltung ist es, Bauingenieurstudenten in die Grundlagen von Flächentragwerken
einzuführen. Das sind statische Modelle bzw. Systeme, die man als
Scheiben, Platten, Schalen und Faltwerke bezeichnet. Im Vergleich zu Stabtragwerken,
die in den Lehrveranstaltungen Statik I bis III behandelt werden, gestaltet sich die
statische Betrachtung von Flächentragwerken erheblich komplizierter, da die Beanspruchung,
ausgedrückt durch Kraft– und Wegzustände, nun von zwei Ortskoordinaten
abhängt und die baustatische Beschreibung daher zwangsläufig auf partielle Differentialgleichungen
(DGL) führt. Einerseits steigt der mathematische Aufwand dadurch erheblich
an und andererseits sind für technisch interessante Anwendungsfälle nur eine
begrenzte Anzahl von analytischen Lösungen bekannt. Um sich diesem Umstand anpassen
zu können, sind zwei stark unterschiedliche Vorgehensweisen zur Behandlung
von Flächentragwerken entstanden.
1. Die Vorgehensweise mit baustatischen Methoden: Sie zielt darauf ab, Flächentragwerke
in anschaulicher Weise durch Stabtragwerke zu ersetzen; z.B. Scheiben
durch Fachwerke und Platten durch Trägerroste oder noch einfacher, Scheiben
durch einen Dreibock und Platten durch ein gekreuztes Balken– bzw.
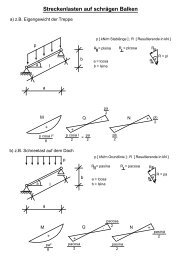
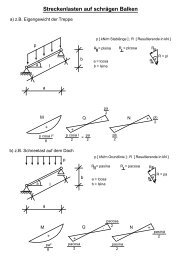
Trägerpaar (Bild 1.1). Solche einfachen Modelle sind immer dann von Nutzen,
wenn es um Scheiben und Platten im Ingenieurhochbau geht, die einen Großteil
der praktischen Ingenieuraufgaben umfassen. Sie sind in den technischen Regelwerken
verankert, z.B. der DIN 1045 und stellen im Zusammenhang mit begleitenden
konstruktiven Maßnahmen ein wichtiges Werkzeug des praktisch tätigen
Ingenieurs dar.
2. Die Vorgehensweise mit mathematisch orientierten Methoden: Sie zielt darauf ab,
entweder die DGL der Flächentragwerke unmittelbar analytisch bzw. numerisch
zu integrieren oder die schwachen Formen der DGL – in der Baustatik als Arbeitsgleichungen
(AGL) des Prinzips der virtuellen Weggrößen (PvW) und des
Prinzips der virtuellen Kraftgrößen (PvK) bekannt – zu nutzen, um Näherungs–
lösungen zu ermitteln. Am Ende dieses Weges steht heute die Methode der finiten
Elemente, kurz Finite–Elemente–Methode (FEM), die in Form von FE–Programmen
ein mächtiges Werkzeug für Ingenieure darstellt, wenn es darum geht,
Lösungen für Flächentragwerke zu finden, z.B. im Anwendungsbereich des
Brücken– und Industriebaus, wo die einfachen baustatischen Methoden ihre Gültigkeit
verlieren.
– 1 / 1 –

Höhe
Wandscheibe
Auflager
Länge
Randlast
Druckstab Druckstab
Dreibock
Zugstab
a) Lastabtragung in einer Wandscheibe durch einen Dreibock
Breite
Länge
– 1 / 2 –
Gelenkige Lagerung
Flächenlast
Platte
b) Lastabtragung in einer Platte durch gekreuzte Balken
Mittelfläche
der Platte
Gekreuzte Balken
Dicke
Mittelfläche
der Scheibe
Bild 1.1 : Einfache Modelle zur Erfassung der Scheiben– und Plattenwirkung
Dicke

Für beide Vorgehensweisen sind genauere Kenntnisse der Theorie der Flächentragwerke
erforderlich, um sie anwenden zu können. Im Fall der baustatischen Methoden,
um eine Abschätzung darüber zu erhalten, welche konstruktiven Maßnahmen erforderlich
sind, um die Defizite von vereinfachten Berechnungen auszugleichen und im Fall
der mathematischen Methoden, z.B. der FEM, um die Sicherheit im Umgang mit FE–
Programmen zu erhöhen.
Die Lehrveranstaltung Statik IV ist in sieben Teilabschnitte gegliedert. Im Teil 1 wird
eine Übersicht über die methodische Vorgehensweise angegeben, und es werden statische
Systeme von Scheiben, Platten, Schalen und Faltwerken vorgestellt. Im Teil 2 erfolgt
die Definition der verwendeten Bezeichnungen am Beispiel eines Ausschnitts aus
einem drei–dimensionalen Kontinuum. Im Rahmen der gesamten Veranstaltung kommt
konsequent die Indexschreibweise zur Anwendung. Einerseits, um die Schreibarbeit
radikal zu verkürzen und andererseits, um die Ähnlichkeiten in der Struktur der Grundgleichungen
zwischen Stab– und Flächentragwerken aufzeigen zu können. Gerade mit
Hilfe dieser Darstellungsform gelingt es in besonders einfacher Weise, das noch un–
bekannte Tragverhalten der Flächentragwerke – Scheibe, Platte, Schale – aus dem
bereits bekannten Tragverhalten der zugeordneten Stabtragwerke – Stab, Balken,
Bogen – zu erkennen und damit einer anschaulichen, also mehr einer ingenieur– als
mathematischen Deutung zugänglich zu machen. Allein dieser Aspekt rechtfertigt
schon die Mühe, die es für Ingenieure i.a. bedeutet, sich in diese moderne Notation einarbeiten
zu müssen, die im Vergleich zur klassischen Darstellungsform zumindest für
Bauingenieure doch sehr mathematisch erscheint. Das ist sie aber ganz und gar nicht,
da Tensoren für Physiker und daher auch für Ingenieure ein ”natürliches Werkzeug” darstellen,
um naturwissenschaftliche Phänomene zu beschreiben.
In den Teilen 3 und 5 werden die Grundlagen der Scheiben–, Platten– und Schalen–
theorie behandelt. Ziel ist es, die sogenannten Scheiben–, Platten– und Schalengleichungen
abzuleiten und analytische Lösungsmöglichkeiten zu diskutieren. Der
Schwerpunkt liegt dabei ganz deutlich bei den Scheiben und Platten. Sie sind aus der
Sicht der Praxis als die wichtigsten Vertreter der Flächentragwerke anzusehen. Die Behandlung
der Schalen beschränkt sich auf die Darstellung des Einflusses der geometrischen
Form und das Aufzeigen von Lösungswegen zur Berechnung von Rotations–
und Membranschalen.
Zum Abschluß werden in den Teilen 6 und 7 Verfahren zur anwendungsorientierten
Berechnung von Scheiben und Platten behandelt. Im Teil 6 die Gitterrost–Methode
(GRM), die zur Gruppe der baustatischen Lösungsmethoden gehört. Durch eine anschauliche
Betrachtung, die von einer strengen statisch–geometrischen Analogie zwischen
Flächen– und Stabtragwerken ausgeht, wird gezeigt, daß sich Scheiben wie
Fachwerke und Platten wie liegende Rahmenwerke bzw. Trägerroste verhalten. Damit
besteht u.a. die Möglichkeit, die aussteifende Wirkung von Scheiben und Platten unmittelbar
in statische Systeme von Stabtragwerken zu integrieren, ohne dabei gleich auf
finite Elemente zurückgreifen zu müssen.
– 1 / 3 –

Finite–Elemente–Methoden gehören zur Gruppe der numerischen Methoden. Es sind
im verstärkten Umfang Betrachtungen aus dem Bereich der analytischen und numerischen
Mathematik erforderlich, um Scheiben– und Plattenelemente zu entwickeln.
Zwar ist es nicht unbedingt notwendig, daß Anwender der FEM die theoretischen
Grundlagen der Methode in allen Einzelheiten beherrschen. Es ist aber unabdingbar,
daß Anwender zumindest das Elementverhalten abschätzen können, um Ergebnisse
zu erzielen, die aus baustatischer Sicht mit der Qualität von Scheiben– und Platten–
lösungen übereinstimmen. Im Teil 7 werden daher einfache Scheiben– und Plattenelemente
vorgestellt, die wie das Verfahren der Stabsteifigkeiten (VdS) aus Statik III auf
dem PvW beruhen. Eine weitergehende systematische Darstellung der FEM erfolgt
im Rahmen der Lehrveranstaltung Vertiefung I /13/, wobei vor allem eine Betrachtung
der Methode aus baustatischer und baudynamischer Sicht im Vordergrund des Interesses
steht.
1.2 Begleitende Literatur
Zur Thematik der Flächentragwerke liegt eine umfangreiche Literatur vor. Zu den Klassikern
gehören die Lehrbücher von Girkmann /1/ und Flügge /2/, die auch heute noch
sehr aktuell sind, wenn es darum geht, sich in die physikalischen und mathematischen
Gegebenheiten von Flächentragwerken einzulesen. Sie behandeln ausschließlich analytische
Lösungsverfahren. Die mathematische Dominanz ist relativ groß. Als eine
moderne Kurzform dieser Lehrbücher ist der Beitrag von Mang in /3/ zu werten, der
in knapper Form alles wesentliche präsentiert, was konstruktive Bauingenieure über
Flächentragwerke wissen müssen.
In dem Lehrbuch von Basar und Krätzig /4/ kommt durchgängig die Indexschreibweise
zur Anwendung, die in vereinfachter Form auch in Statik IV verwendet wird. Dieses
Lehrbuch, das die Mechanik der Flächentragwerke einheitlich vom Standpunkt gekrümmter
Flächen aus behandelt, stellt daher an den Leser zwangsläufig sehr hohe mathematische
Ansprüche. Es wird aber trotzdem als Hintergrundlektüre empfohlen, weil
es ein sehr modernes Konzept zur Behandlung von Flächentragwerken darstellt, auf
das u.a. die FEM der Flächentragwerke beruht. Das Lehrbuch von Eschenauer und
Schnell /5/, das in kurzer, aber durchaus vollständiger Form die Grundlagen der Scheiben,
Platten und Schalen behandelt, kann ebenfalls als begleitende Lektüre empfohlen
werden. Ein besonderer Vorteil dieses Lehrbuchs ist, daß es neben der klassischen
Darstellungsform auch die Indexschreibweise verwendet und somit das Verständnis für
die Indexschreibweise erhöht.
Die Abhandlungen von Schleeh /6/, Pieper, Martens /7/, Markus /8/ und Grasser,
Thielen /9/ sind dagegen vorrangig als Tabellenwerke zu nutzen. Sie sind von prak–
tischem Wert, wenn es darum geht, Untersuchungen von Flächentragwerken per
Handrechnung vorzunehmen. Im Rahmen von Statik IV stellen sie z.B. ein wichtiges
Hilfsmittel dar, um Übungen durchführen und Hausaufgaben anfertigen zu können.
– 1 / 4 –

In der Abhandlung Elementmethode der Elastostatik von Zimmer und Grothe /10/ werden
Modelle der GRM vorgestellt und Anwendungen zur Lösung von praktischen Ingenieuraufgaben
gezeigt. Auf dem Gebiet der Konstruktionsberechnung mit Element–
methoden repräsentiert sie den Stand der Technik zu Beginn der 70er Jahre.
Zwischenzeitlich ist die in /10/ propagierte Konzeption methodisch überholt. Aus heutiger
Sicht liegt ihr Wert vor allem in der auf Anschauung begründeten Vorgehensweise.
Für konstruktive Bauingenieure ist die Abhandlung /10/ daher nach wie vor lesenswert.
Das Lehrbuch Finite Elemente von Knothe und Wessels /11/ repräsentiert dagegen den
Stand der Technik der 90er Jahre. Trotz der Beschränkung auf Weggrößenele–
mente ist es als Eingangslektüre in die Problematik der FEM sehr zu empfehlen, da
es alle wesentlichen Schritte der Methode sowohl auf Element– als auch auf System–
ebene sehr ausführlich behandelt. Die Vorgehensweise in /11/ ist mit dem VdS aus der
Statik III /12/ vergleichbar. Sie ist aber allgemeiner, weil neben Stab– zusätzlich auch
Flächentragwerke betrachtet werden. Im Rahmen der Statik–Lehrveranstaltungen geschieht
dies in voller Allgemeingültigkeit erst in der nachfolgenden Vertiefung I: Finite–
Elemente–Methode in der Baustatik und Baudynamik, in der dann auch moderne gemischt–hybride
Elementkonzepte vorgestellt werden /13/.
1.3 Statische Modelle
Tragwerke sind, wie es der Name sehr treffend ausdrückt, der tragende Teil von Bauwerken.
Entwurf, Konstruktion und rechnerischer Nachweis in Form einer statischen
Berechnung sind Tätigkeiten, die in der Baupraxis konstruktiv ausgebildete Bauingenieure
wahrnehmen.
Im Rahmen des Entwurfprozesses sind vor allem zwei Maßnahmen von dominanter Bedeutung:
Die Entwicklung einer tragenden Konstruktion, die immer im Mittelpunkt des
Interesses stehen sollte und die Modellierung des zugehörigen statischen Systems, das
die Grundlage der statischen Berechnung bildet, um das Tragverhalten von Bauwerken
rechnerisch nachvollziehen zu können.
Bei der Modellierung von statischen Systemen sind die physikalischen Zustände im
Tragwerk so wirklichkeitsnah wie möglich, dabei aber so einfach wie nötig abzubilden.
Diese Vorstellung ist als oberstes Gebot bei der Lösung dieser sehr anspruchvollen Ingenieuraufgabe
zu beachten. Sie läßt sich immer dann umsetzen, wenn man mit eindeutig
definierten statischen Modellen arbeitet, die beim Lastabtrag spezielle Aufgaben
erfüllen.
Wichtige Einflußparameter zur Klassifizierung von statischen Modellen sind
– die geometrische Form der tragenden Bauteile
und
– die Art und Weise, wie Einwirkungen tragende Bauteile beanspruchen.
– 1 / 5 –

Alle Bauteile sind im Hinblick auf ihre geometrische Form immer als dreidimensionale
Gebilde anzusehen. Trotzdem werden sie im statischen System nur in Ausnahmefällen
auch in allen drei Dimensionen erfaßt. Für die Mehrzahl der Anwendungsfälle reicht es
aus, Tragwerke als Stabtragwerke zu modellieren. Dies trifft immer dann zu, wenn zwei
Abmessungen eines Bauteils, nämlich die des Querschnitts im Vergleich zur dritten Abmessung,
der Länge klein ausfallen. Dabei können die einzelnen Bauteile auf einer
Linie, in einer Ebene oder im Raum angeordnet und gelenkig oder biegesteif miteinander
verbunden sein. Ergibt sich aus der Einwirkung lediglich eine Beanspruchung in
Richtung der Stabachsen, bezeichnet man die statischen Modelle bei Anordnung auf
einer Linie als (Druck– Zug)–Stäbe und bei Anordnung in einer Ebene oder im Raum
als Fachwerke. Erfolgt die Einwirkung dagegen senkrecht zur Stabachse, bezeichnet
man die statischen Modelle als Balken oder Rahmenwerke. Sind die Stabachsen nicht
gerade sondern gekrümmt, werden die statischen Modelle als Bogenwerke bezeichnet.
Der Übergang von den Stab– zu den Flächentragwerken ist dadurch gekennzeichnet,
daß nun zwei Abmessungen eines Bauteils, nämlich die Länge und Höhe oder die
Länge und Breite als dominant zu betrachten sind, während die dritte Abmessung, die
Dicke im Vergleich dazu deutlich kleiner ausfällt, vgl. (Bild 1.1). Der Übergang zwischen
Stab– und Flächentragwerken ist fließend. Ob eine stabförmige Modellierung eines
Bauteils ausreicht oder ob bereits eine Erfassung als Flächentragwerk erforderlich ist,
muß daher von Fall zu Fall in Abhängigkeit der speziell vorliegenden Bedingungen entschieden
werden.
Treten die Einwirkungen parallel zur Fläche auf, bezeichnet man das statische Modell
als Scheibe (Bild 1.2), die eine flächige Erweiterung des statischen Modells (Druck–
Zug)–Stab darstellt. Treten die Einwirkungen dagegen senkrecht zur Fläche auf, bezeichnet
man das statische Modell als Platte (Bild 1.3), die eine flächige Erweiterung
des statischen Modells Balken darstellt. Ist die Fläche zusätzlich gekrümmt und treten
Einwirkungen parallel und senkrecht oder nur parallel oder nur senkrecht zur Fläche
auf, erhält man das statische Modell einer Schale (Bild 1.4).
Neben Scheibe, Platte und Schale ist noch das statische Modell Faltwerk (Bild 1.5)
zu definieren. Faltwerke sind als Zwischenstufe zwischen ebenen und gekrümmten
Flächentragwerken anzusehen. Sie bestehen aus räumlich angeordneten Scheiben
und Platten, die man als Falten bezeichnet. Die Falten sind entlang der Kanten, an denen
die ebenen Teilflächen der Falten zusammenstoßen, gelenkig oder biegesteif miteinander
verbunden. Aus baustatischer Sicht verhalten sich Faltwerke wie Schalen, die
an Stelle einer stetigen eine unstetige Geometrie aufweisen.
Der Übergang von den Flächen– zu den Volumentragwerken ist dadurch gekennzeichnet,
daß nun alle drei Abmessungen eines Bauteils in gleicher Größenordnung auf–
treten. Eine weitere Klassifizierung ist dann nicht mehr möglich. In der statischen Berechnung
zur Ermittlung der Kraft– und Wegzustände sind alle drei Abmessungen unabhängig
voneinander zu erfassen. Im Bauwesen spielen dreidimensionale statische
Modelle i.a. nur eine untergeordnete Rolle. Wenn sie vorkommen, so fast ausschließlich
im Bereich des Grundbaus, um den Lasteintrag in den Baugrund genauer zu unter–
suchen. Der Baugrund unter dem Faltwerk im (Bild 1.5) ist z.B. dreidimensional abgebildet,
um die Wechselwirkung zwischen Bodenplatte und Baugrund in die statische
Berechnung mit einzubeziehen, vgl. hierzu die (Bilder 1.5.1 und 1.5.2).
– 1 / 6 –

1.4 Vorgehensweisen und Berechnung
Das Ziel einer statischen Berechnung von Tragwerken ist es, die Beanspruchung S
(stress) zu ermitteln, um sie mit der Beanspruchbarkeit R (resistance) vergleichen zu
können. Es ist nachzuweisen, daß
S d / R d ≤ 1 (1.1)
uneingeschränkt für alle kritischen Punkte im Tragwerk gilt. Der Index d (design) gibt
an, daß der Nachweis für Bemessungswerte zu erfolgen hat.
In der Regel sind die Beanspruchungen mit den Bemessungswerten der Einwirkungen
zu bestimmen. Die Klassifizierung der Beanspruchung in den statischen Modellen von
Bauteilen oder Tragwerken ist in (Tabelle 1.1) angegeben. Für Stab– und Flächentragwerke
ist eine eindeutige physikalische Zuordnung möglich. In (Druck– Zug)–Stäben
tritt ein eindimensionaler und in Scheiben ein zweidimensionaler Dehnungszustand auf,
während sich in Balken ein eindimensionaler und in Platten ein zweidimensionaler Biegezustand
einstellt. Bei Bögen und Schalen kommt es durch die stetige Systemverkrümmung
zu einer Kopplung der Dehn– und Biegebeanspruchung, die sich wegen der
unstetigen Systemkrümmung auch bei Faltwerken einstellt. Bei Volumentragwerken ist
dagegen immer von einem dreidimensionalen Beanspruchungszustand auszugehen,
der Dehn– und Biegeanteile enthält. Es hängt vorrangig vom Einwirkungszustand ab,
welcher Anteil sich als dominant erweist.
In Abhängigkeit vom gewählten Nachweisverfahren kann die Bedingung (1.1) als
Spannungsnachweis, als Schnittgrößennachweis, als Bauteilnachweis oder als Tragwerksnachweis
erfüllt werden. Berechnungsgrundlage im Rahmen von Statik IV sind
ausschließlich linear–elastische Theorien, so daß die Ermittlung der Zustandsgrößen
– Schnittgrößen und zugehörige Verschiebungen und Verdrehungen – im Mittelpunkt
des Interesses steht. Lösungswege und Lösungsmethoden zur Ermittlung von Zustandsgrößen
sind in (Tabelle 1.2) angegeben.
Es sind immer die Grundgleichungen abzuleiten, die das Gleichgewicht und die Verträglichkeit
von Flächentragwerken in Form von DGL beschreiben. Grundgleichungen sind
Definitionsgleichungen des Tragverhaltens. Im Rahmen der Stabstatik kommen z.B.
das Schnittprinzip, die Mohr–Analogie, das Kraftgrößenverfahren und das Weggrößenverfahren
zum Einsatz, um die direkte Integration der DGL zu vermeiden. Für Flächentragwerke
sind solche anschaulichen Verfahren nur für spezielle Sonderfälle bekannt,
so daß die Lösungswege zur Ermittlung der Zustandsgrößen auf Vorgehensweisen beruhen,
die entweder unmittelbar von der DGL selbst oder von der zugeordneten AGL,
also der schwachen Form der Differentialgleichungen ausgehen.
– 1 / 7 –

Stabtragwerke (1D)
Stab
Balken
Bogen
Fachwerke,
Rahmen–
werke
Statische Modelle
Flächentragwerke (2D) Volumentragwerke (3D)
Scheibe
Platte
Schale
Faltwerke
Tabelle 1.1 : Klassifizierung der Beanspruchung in statischen Modellen
– 1 / 8 –
Keine weitere
Klassifizierung
möglich !
Klassifizierung der Beanspruchung
Dehnung Biegung Dehnung und Biegung
Stabtragwerke
Stab
Balken
Bogen
Flächentragwerke mit polygonartiger Begrenzung
Scheibe
Platte
Schale
Flächentragwerke mit rotationssymmetrischer Begrenzung
Kreisscheibe
Volumentragwerke
Kontinuum
Kreisplatte
Rotationsschale

Baustatische Methoden
Scheiben:
Verfahren von
Schleeh.
Ermittlung von Zustandsgrößen
Ableitung der Grundgleichungen
Lösungswege
Differentialgleichungen (DGL) Arbeitsgleichungen (AGL)
Reduzierung der Grundgleichungen
zu integrierbaren DGL–Systemen
bzw. einer DGL von hoher Ordnung.
Lösungsmethoden
Tabelle 1.2 : Lösungswege und Lösungsmethoden zur Ermittlung von Zustandsgrößen
– 1 / 9 –
Indirekte Integration der Grund–
gleichungen zu AGL durch
Anwendung der Prinzipe der virtuellen
Weg– und Kraftgrößen.
Analytische Methoden Numerische Methoden
Allgemein Speziell DGL AGL DGL AGL
Gitterrost–
methode
(GRM),
einfache Stab–
und Balken–
modelle.
Platten:
Verfahren von
Pieper/Martens.
Schalen:
KGV für zu–
sammenge–
setzte Rota–
tionsschalen.
Direkte
Integration,
Reihen–
ansätze.
Ritz,
Trefftz,
Galerkin,
Fehler–
quadrat–
ausgleich.
Einflußflächen
Differenzen–
verfahren,
Mehrstellen–
verfahren,
Kollokation.
Finite–
Element–
Methode
(FEM),
Rand–
Element–
Methode
(REM).

Bei den Lösungsmethoden zur Durchführung von Zahlenberechnungen ist zwischen
baustatischen, analytischen und numerischen Methoden zu unterscheiden. In der Baupraxis
kommen wegen des zunehmenden Rechnereinsatzes fast nur noch numerische
Methoden zum Einsatz. Im Rahmen dieser Klasse ist die FEM /11/ von absoluter Dominanz.
Trotzdem sind die baustatischen und analytischen Methoden nicht ohne Bedeutung.
Baustatische Methoden, wie z.B. das Verfahren von Schleeh /6/ für Scheiben oder
das Verfahren von Pieper/Martens /7/ sind vor allem im Rahmen von Kontrollbe–
rechnungen oder statischen Prüfungen nach wie vor beliebt. Das Gleiche gilt für das
Kraftgrößenverfahren von zusammengesetzten Rotationsschalen, das sich im Zusammenhang
mit den Markus–Tabellen /8/ als ein geeignetes Verfahren erweist, um FE–Ergebnisse
von Behältern zu überprüfen.
Von besonderem Interesse ist die GRM /10/. Sie ersetzt in statisch gleichwertiger Weise
u.a. Scheiben durch Fachwerke und Platten durch liegende Rahmenwerke bzw. Trägerroste.
Sie erreicht zwar bei weitem nicht die Leistungsfähigkeit der FEM, zeichnet sich
aber im Vergleich zur FEM durch eine besonders große baustatische Anschaulichkeit
aus. Schon allein aus didaktischen Gründen sollte man daher auf die Vorstellung dieser
Methode nicht verzichten. Vor allem dann nicht, wenn es vorrangig darum geht, Bau–
ingenieurstudenten in die Grundlagen der Statik der Flächentragwerke einzuführen.
Aber auch zur Absicherung einfacher Stab– und Balkenmodelle ist die GRM hervor–
ragend geeignet.
Gleiches gilt auch für die analytischen Methoden. Sie haben zwar keinen unmittelbaren
Anwendungswert, ihre Kenntnis ist aber unabdingbar, um das Tragverhalten von
Flächentragwerken im Detail zu verstehen, vgl. z.B. /1/, /2/ und /3/.
Aus der Vielzahl der Lösungsmethoden werden im Rahmen von Statik IV nur einzelne
Methoden genauer behandelt. Dies sind
– bei Scheiben das Verfahren von Schleeh, die GRM und die FEM,
– bei Platten Reihenansätze, das Ritz–Verfahren, die GRM und die FEM
sowie
– bei Schalen das KGV für zusammengesetzte Rotationsschalen und die Mem–
brantheorie von allgemeinen Schalen.
1.5 Anwendungsbeispiele
Es sind vorrangig theoretisch orientierte Betrachtungen erforderlich, um Grundlagen,
Lösungswege und Lösungsmethoden zur Berechnung von Flächentragwerken abzuleiten.
Zuvor werden aber vier charakteristische Anwendungsbeispiele vorgestellt, nämlich
eine Scheibe, eine Platte, eine Schale und ein Faltwerk, um den praktischen Nutzen
dieser Betrachtungen zu verdeutlichen. Alle Berechnungen werden mit dem FE–Programm
GEMAS des Fachgebiets Statik der Baukonstruktionen durchgeführt, indem
ausschließlich gemischt–hybride Elementvarianten implementiert sind /13/. Die maßgeblichen
Ergebnisse sind entweder als Höhenstreifen oder Trajektorien in der Fläche
der betrachteten Tragwerke oder als Schnitte dargestellt.
– 1 / 10 –

1.5.1 Wandscheibe
Das erste Beispiel ist eine Wandscheibe aus Stahlbeton. Das Berechnungssystem ist
im (Bild 1.2) dargestellt. Die Konstruktion ist 33.70 m lang und 11.00 m hoch. Die Dicke
schwankt zwischen 0.50 und 1.00 m. Sie ist nur in einem Teilbereich auf Pfählen gegründet,
so daß sich links und rechts von der Pfahlgründung große Auskragungen ergeben,
vgl. (Bild 1.2). Im Berechnungssystem wird die Pfahlgründung, die aus 20 Bohrpfählen
von 0.60 m Durchmesser und 9.00 m Länge besteht, durch Vertikal– und
Horizontalfedern erfaßt. Die Steifigkeit der Vertikalfedern ist pro Pfahl zu berechnen. Sie
beträgt C V = EA Pfahl / L Pfahl ≈ 10 6 kN/m. Für die Horizontalfedern sind 30% von diesem
Wert anzunehmen. Es gilt C H = 0.3 C V.
Wandscheiben dienen vorrangig zur Aussteifung von großen Gebäuden und nachrangig
zur Ableitung großer Vertikallasten in den Baugrund. Das System im (Bild 1.2) ist
z.B. als Querscheibe in einem Krankenhaus angeordnet. Die einwirkenden Vertikallasten
sind zu resultierenden Einzellasten zusammengefaßt. Die genauen Angriffspunkte
sind in Abhängigkeit der vorgegebenen Abmessung zu schätzen.
Die Elementierung der Wandscheibe (Bild 1.2) erfolgt mit 961 finiten Vierecks–
Scheibenelementen. Dadurch ergeben sich 1063 gemeinsame Knotenpunkte. Die
Knotenpunkte sind Informationsträger der Verschiebungen u 1 (cm) und u 2 (cm) , die
sich infolge der Einwirkungen in Längs (X 1 bzw. X)– und Höhenrichtung (X 2 bzw. Y)
einstellen. Die Höhenstreifen der vertikalen Verschiebungskomponente u 2 in der
verformten Fläche sind im (Bild 1.2.1) dargestellt. Durch die ausschließlich vertikale
Lastrichtung fallen die Werte der horizontalen Verschiebungskomponente u 1 sehr klein
aus. Auf eine Darstellung wird daher verzichtet.
Die Elemente sind Informationsträger der Kräfte n 11 (kN/cm), n 22 (kN/cm) und
n 12 = n 21 (kN/cm), die sich infolge der Einwirkungen in der Scheibe einstellen. Die
Kraft n 11 tritt in allen Querschnitten Höhe × Dicke entlang der Längskoordinate X 1
auf und die Kraft n 22 in allen Querschnitten Länge × Dicke entlang der Höhenkoordinate
X 2 . Ihre Verteilung in der unverformten Fläche in Form von Höhenstreifen ist in den
(Bildern 1.2.2 und 1.2.3) dargestellt. n 11 ist auf die Höhe und n 22 auf die Länge der
Wandscheibe bezogen. Die Kräfte n 12 = n 21 erfassen die Wechselwirkung zwischen
diesen Richtungen, die sich aus dem flächigen Verhalten von Scheiben ergibt. Dieser
Effekt stellt im Vergleich zur Theorie der (Druck– und Zug)–Stäbe das eigentliche Neue
der Scheibentheorie dar und ist ohne Kenntnis dieser Theorie nicht zu erklären. Die Verteilung
der Kräfte n 12 = n 21 in der unverformten Fläche in Form von Höhenstreifen ist
im (Bild 1.2.4) dargestellt.
Die erzielten Ergebnisse sind aus baustatischer Sicht plausibel. Mit Hilfe von (Bild 1.2.1)
kann der Verschiebungszustand kontrolliert und mit Hilfe der (Bilder 1.2.2 bis 1.2.4) die
Bemessung der Wandscheibe durchgeführt werden.
– 1 / 11 –

– 1 / 12 –
4. m
1.50 m
X 2 (Y), u 2
3. m
4. m
11. m 9. m Bild 1.2 : Wandscheibe
0.60 m
2700 kN
240 kN
0.90 m
13.70 m
1.60 m
Dicke t = 0.50 m
600 kN
0.50 m
0.50 m
4000 kN
1900 kN
1500 kN
1490 kN
1560 kN
4.70 m 3.20 m 12.60 m
5.00 m 15.00 m
1100 kN
640 kN
470 kN
Dicke t = 0.70 m
640 kN
20 Bohrpfähle,Durchmesser 0.60 m, L = 9.00 m
n 22
33.70 m
n 21 = n 12
n 12
Dicke t = 1.00 m
n 11
Stahlbeton :
E = 3 ⋅ 107 kN/m2 ,
ν = 0.20.
3500 kN
X 1 (X), u 1
10.20 m 3. m
6. m
2. m 3. m

– 1 / 13 –
Y
Z
X
Bild 1.2.1 : Wandscheibe. Verschiebung u2 (cm).
2.51+00
2.28+00
2.05+00
1.82+00
1.59+00
1.37+00
1.14+00
9.11–01
6.83–01
4.56–01
2.28–01
1.95–04

– 1 / 14 –
Y
Z X
�������������������������������������������������������
1.05+02
8.30+01
6.07+01
3.84+01
1.61+01
–6.21+00
–2.85+01
–5.08+01
–7.31+01
–9.55+01
–1.18+02
–1.40+02

– 1 / 15 –
Y
Z
X
Bild 1.2.3 : Wandscheibe. Verteilung von n22 (kN/cm).
4.23+01
3.20+01
2.16+01
1.12+01
8.49–01
–9.52+00
–1.99+01
–3.03+01
–4.06+01
–5.10+01
–6.14+01
–7.18+01

– 1 / 16 –
Y
Z X Bild 1.2.4 : Wandscheibe. Verteilung von n12 = n21 (kN/cm).
2.79+01
2.29+01
1.78+01
1.28+01
7.79+00
2.76+00
–2.26+00
–7.29+00
–1.23+01
–1.73+01
–2.24+01
–2.74+01

1.5.2 Flach– und Pilzdecke
Das zweite Beispiel ist eine Flach– und Pilzdecke aus Stahlbeton. Der Berechnungsausschnitt,
der ein Eckfeld sowie Rand– und Innenfelder umfaßt, ist im (Bild 1.3) dargestellt.
Die regelmäßige Spannweite der Plattenfelder zwischen den Stützenreihen beträgt
in X 1 – Richtung 10.00 m und in X 2 – Richtung 8.00 m. Die Dicke der Platte soll
durchgängig 0.25 m betragen. Zusätzliche Verstärkungen im Bereich der Stützen,
auch Pilzköpfe genannt, beeinflussen das Verformungsverhalten zwar sehr günstig,
sind aus bautechnischen Gründen i.a. aber unerwünscht. Punktgestützte Platten ohne
Pilzköpfe bezeichnet man als Flachdecken. Geeignete baupraktische Näherungs–
verfahren zur Berechnung von Flach– und Pilzdecken sind /9/ zu entnehmen. Der
Anwendungsbereich dieser Verfahren ist aber auf regelmäßige Stützenraster beschränkt,
also Systemen, die hinsichtlich der Konfiguration mit dem System im (Bild 1.3)
übereinstimmen.
Mit der FEM können dagegen Systeme wie im (Bild 1.3), aber auch beliebig berandete,
gestützte und belastete Flach– und Pilzdecken berechnet werden. Die Elementierung
des Systems im (Bild 1.3) als punktgestützte Flachdecke erfolgt mit 2279 finiten Vierecks–
Plattenelementen, so daß sich 2376 gemeinsame Knotenpunkte ergeben. Für
den Lastfall Eigengewicht ist die Durchbiegung u 3 (m) im (Bild 1.3.1) dargestellt. Die
Verteilung der Biegemomente m 11 (kN/m) und m 22 (kN/m) in Form von Höhenstreifen
ist in den (Bildern 1.3.2 und 1.3.3) dargestellt und die Verteilung des Torsionsmoments
m 12 = m 21 (kNm/m) im (Bild 1.3.4).
Die Welligkeit im Verlauf der Durchbiegung (Bild 1.3.1) ist eine Folge der Punktstützung.
Die Biegemomente m 11 (Bild 1.3.2) und m 22 (Bild 1.3.3) können dagegen in relativ
regelmäßige Gurt– und Feldstreifen unterteilt werden. Die Gurtmomente treten im Stützenbereich
und die Feldmomente dazwischen auf. Diese Unterteilung ist als ein charakteristisches
Merkmal von Flach– und Pilzdecken zu werten. Die Vorgabe von Gurt– und
Feldstreifen bildet daher oft die Grundlage von Näherungslösungen, vgl. z.B. /9/. Die
Bezugsfaser ist wegen der nach oben gerichteten X 3 – Koordinate auf der oberen Plattenseite
angeordnet, vgl. (Bild 1.3). Diese Zuordnung ist bei der Betrachtung der Ergebnisbilder
zu beachten. Für die Gurtmomente ergeben sich zwar positive und für die Feldmomente
negative Werte. Die Lage der Bewehrung ändert sich dadurch aber nicht. Im
Stützenbereich tritt bei positivem Moment an der Plattenoberseite Zug auf, und im Feldbereich
tritt bei negativem Moment an der Plattenunterseite Zug auf, die Bewehrung
muß also im Gurtstreifen oben und im Feldstreifen unten liegen.
Im (Bild 1.3.4) ist die antimetrische Verteilung der Torsionsmomente besonders deutlich
zu erkennen. Die Werte sind in der unmittelbaren Nähe der Stützen größer als im Feld,
weil die Punktstützung die freie Durchbiegung in Richtung der beiden Plattenspann–
weiten stark behindert. Als Reaktion darauf kommt es zu einer starken Verwindung der
Plattenfläche. Dies führt zu Torsionsmomenten, die als zusätzliche Bemessungsgrößen
das eigentlich Neue der Plattentheorie darstellen.
– 1 / 17 –

Freier
Rand
H
X 2 (Y)
a 2
2
Freier Rand
a 2
a 1
2 a 1
r 1 L 11 L 12 L 13
X 3 (Z), u 3
m 22
m 21
Bild 1.3 : Flach– und Pilzdecke
m 11
m 12
p 3
L 11 = L 12 = L 13 = 10.00 m, L 21 = L 22 = L 23 = 8.00 m,
r 1 = r 2 = 1.50 m, a 1 = a 2 = 2.00 m,
tp = 0.25 m, tk = 0.50 m, H = 4.00 m.
Stahlbeton : E = 3⋅107 kN/m, ν = 0.20.
Eigengewicht : p3 = p3 (γ, t) = – 25tp = – 6.25 kN/m2 .
– 1 / 18 –
r 2
L 21
L 22
L 23
X1 (X)
Symmetrie–
linien
t p t k
X 1 (X)

– 1 / 19 –
Z
Y
X
Bild 1.3.1 : Flachdecke. Durchbiegung u3 (m).
1.13–02
1.03–02
9.24–03
8.21–03
7.18–03
6.16–03
5.13–03
4.11–03
3.08–03
2.05–03
1.03–03
–9.31–10

– 1 / 20 –
Y
Z
X
Bild 1.3.2 : Flachdecke. Verteilung von m11 (kNm/m).
2.09+02
1.86+02
1.63+02
1.39+02
1.16+02
9.24+01
6.90+01
4.56+01
2.22+01
–1.26+00
–2.47+01
–4.81+01

– 1 / 21 –
Y
Z
X
Bild 1.3.3 : Flachdecke. Verteilung von m22 (kNm/m).
1.73+02
1.55+02
1.36+02
1.17+02
9.84+01
7.96+01
6.08+01
4.21+01
2.33+01
4.57+00
–1.42+01
–3.29+01

– 1 / 22 –
Y
Z
X
Bild 1.3.4 : Flachdecke. Verteilung von m 12 = m 21 (kNm/m)
1.72+01
1.46+01
1.20+01
9.34+00
6.71+00
4.08+00
1.45+00
–1.18+00
–3.81+00
–6.45+00
–9.08+00
–1.17+01

1.5.3 Behälter
Das dritte Beispiel ist ein Behälter von rotationssymmetrischer Schalenform aus Stahl,
der zur Aufnahme von flüssigen Füllgütern dient. Das Berechnungssystem ist im
(Bild 1.4) dargestellt. Der zylindrische Mittelteil von 10.00 m Höhe und 10.00 m Durchmesser
lagert auf einer ebenfalls zylindrischen Standzarge von 0.50 m Höhe auf. Der
Auflagerbereich ist durch eine ringförmige Scheiben–Platten–Steife verstärkt, um die
Gefahr des Ausbeulens zu verringern. Der Behälter ist nach unten durch einen 5.00 m
hohen Kegelboden und nach oben durch eine Kugel–Torus–Kappe abgeschlossen.
Die Standzarge liegt auf vier dreiwertigen Linienlagern auf, die sich jeweils über eine
Elementlänge erstrecken. Für jedes Linienlager sind zwei Knoten zu sperren. Sie sind
im Abstand von 90° auf dem Breitenkreis angeordnet, so daß sich trotz der rotationssymmetrischen
Behältergeometrie und des rotationssymmetrischen Lastfalls Füllungsdruck
ein nichtrotationssymmetrischer Beanspruchungszustand in der Behälterwand
einstellt. Der Füllungsdruck ist höhenabhängig und wirkt jeweils senkrecht zur Behälterwand.
Er tritt im Zylinder und im Kegelboden auf. Die Blechdicken betragen im oberen
Bereich t = 8. mm, im mittleren Bereich t = 10. mm und im unteren Bereich t = 12. mm.
Ebene Flächentragwerke, wie z.B. die Wandscheibe im (Bild 1.2) oder die Flach– und
Pilzdecke im (Bild 1.3), sind geometrisch in eindeutiger Weise durch ortsfeste karte–
sische Koordinaten in der (X 1 – X 2 )– Ebene zu beschreiben. In diesen Koordinaten sind
auch die Zustandsgrößen von Scheiben und Platten definiert. Auf gekrümmte Flächentragwerke
ist diese Vorgehensweise aber nicht zu übertragen. Vor allem dann nicht,
wenn sie sich aus Teilschalen zusammensetzen, die unterschiedliche Geometrien
aufweisen. Dies ist z.B. beim Behälter (Bild 1.4) der Fall. Zur geometrischen Beschreibung
des Gesamtsystems ist es erforderlich, jeder Teilschale unabhängige gekrümmte
Flächenkoordinaten (Θ 1 , Θ 2 ) zuzuordnen, die als körperfeste Koordinaten jeweils nur
für eine Teilschale gelten. Mit Θ 1 und Θ 2 ist auch die Schalennormale Θ 3 der Teilschalen
bekannt. Der Zusammenhang mit den ortsfesten kartesischen (X 1 , X 2 , X 3 )– Koordinaten,
die für alle Teilschalen gelten, ist zusätzlich durch eine geeignete Parameterabbildung
anzugeben.
X 1 � X 1 (� 1 , � 2 )
X 2 � X 2 (� 1 , � 2 )
X 3 � X 3 (� 1 , � 2 )
– 1 / 23 –
(1.2)
Wird Gl. (1.2) für jede Teilschale durch analytische Formfunktionen konkretisiert, kann
man die unterschiedlichen Teilschalen in eindeutiger Weise zusammenbauen und damit
auch berechnen. Die Zustandsgrößen der einzelnen Teilschalen sind in den körperfesten
(Θ 1 , Θ 2 )– Koordinaten definiert; die Schnittgrößen immer, die Weg– und Lagergrößen
können alternativ auch in den ortsfesten (X 1 , X 2 , X 3 )– Koordninaten
ausgegeben werden.

Rotations–
achse
Meridian–
richtung
Druck–
höhe
Stahl:
E = 2.1 ⋅ 10 8 kN/m 2 ,
ν = 0.3.
Füllung:
γ = 12 kN/m 3 .
X 1
Z
Konstruktionsprinzip
Einwirkung
Bild 1.4 : Behälter
X 3
Kugel, t = 8 mm
R Ko � 5.00 m
Kegelboden, t = 12 mm
R Ku � 0.30 m
Ortsfeste Koordinaten im Raum
:
:
Θ 2 , u 2
Körperfeste
Koordinaten
in der Fläche
R Z � 5.00 m
R T � 1.00 m
R K � 24.03 m
X 2
Ein– oder mehrschüssiger Aufbau aus rotationssym–
metrischen Schalenformen: Scheibe / Platte, Zylinder,
Kegel, Kugel, Torus und ggf. Ellipsoid und Hyperboloid.
Füllungsdruck p 3 = γ ⋅ Z (kN/m 2 ) mit
γ = spezifisches Gewicht der Füllung und
Z = Druckhöhe.
– 1 / 24 –
Ringrichtung
Torus, t = 8 mm
m 22
Θ 1 , u 1
n 22
Θ 3 , p 3 , u 3
Zylinder, t = 10 mm
m 11
n 11
Ringsteife, t = 12 mm
0.50 m
Standzarge mit 4 dreiwertigen
Linienlagern im Abstand von 90°
10. m
5. m

Die Elementierung des ganzen Behälters erfolgt mit 3680 ”echten” Schalenelementen.
”Echte” Schalenelemente sind finite Elemente mit der speziellen Eigenschaft, daß sie
die Geometrie der Teilschalen analytisch exakt erfassen. In Ringrichtung des Behälters
werden jeweils 40 Elemente angeordnet und in Meridianrichtung für die Kugelkappe
10, für den Übergangstorus 4, für den Zylinder 12, für die Ringsteife 3, für die zylin–
drische Standzarge 3, für den Kegelboden 20 und für den Abschluß des Kegelbo–
dens 3, vgl. (Bild 1.4). Eine Gesamtansicht der Elementierung der verformten Struktur
des Behälters ist im (Bild 1.4.1) dargestellt. Sie enthält 3720 Knoten, an denen die Verschiebungen
und Verdrehungen – hier in Richtung der (Θ 1 , Θ 2 , Θ 3 )– Koordinaten –
berechnet werden.
Bild 1.4.1 : Behälter. Elementierung und verformte Struktur
– 1 / 25 –

Die Beulen in der Behälterwand sind deutlich zu erkennen. Wegen der Systemverkrümmung
wird sie auf Dehnung und Biegung beansprucht, obwohl der Füllungsdruck nur
senkrecht auf die Wand einwirkt. Der Kegelboden muß das Gewicht der Füllung voll abtragen.
Er hängt sich wegen der fehlenden stetigen Unterstützung der Standzarge in
den Zylinder ein und will ihn durch die Umlenkwirkung im Knick zwischen Kegel und Zylinder
nach innen ziehen. Im Bereich der vier, im Abstand von 90° angeordneten Linienlager
ist diese Bewegung aber behindert, so daß die Zylinderwand in Ringrichtung in
Form einer n = 4 Welle ausbeult.
Die weitere Auswertung der Ergebnisse erfolgt in Ringschnitten in der Mitte und am
Ende des Zylinders kurz vor dem Übergang zum Kegelboden (Bilder 1.4.2 bis 1.4.4).
Die Verschiebungen u 3 (m) senkrecht zur Behälterwand sind im (Bild 1.4.2) dargestellt.
6.00–03
4.00–03
2.00–03
–2.00–03
–4.00–03
–6.00–03
0.
u 3 (m)
–1.80+02 –1.20+02 –6.00+01 0. 6.00+01 1.20+02 1.80+02
Bild 1.4.2 : Behälter. Durchbiegung in Ringschnitten.
– 1 / 26 –
Mitte Zylinder
Untere Ende Zylinder
� 1 (Grad)
Die n = 4 Welle im Verschiebungsverlauf der Ringrichtung ist deutlich zu erkennen.
Trotz der Füllung, die auf die Wand von innen nach außen drückt, verschiebt sich die
Wand stärker nach innen als nach außen, wirkt also der Einwirkung entgegen. Dies ist
eine Folge des komplexen Zusammenspiels der Teilschalen. Es wirkt sich besonders
in den Bereichen des Behälters aus, wo Teilschalen zusammenstoßen. Die Amplituden

in der Mitte des Zylinders erreichen Werte von der Hälfte der Wanddicke. Der Einfluß
der Theorie II. Ordnung auf die Stabilität des Gleichgewichtszustandes ist daher nicht
mehr zu vernachlässigen.
Die Membrankräfte in den Ringschnitten sind in den (Bildern 1.4.3a und b) dargestellt.
Sie geben den Scheibenanteil der Schalenlösung an. Der ungestörte Verlauf der Ringzugkraft
n 11 im (Bild 1.4.3a) ist in einfacher Weise durch die Faßformel zu kontrollieren.
Es gilt: n 11 = p 3 ⋅ R, vgl. Abschnitt 5. Der Füllungsdruck auf die Schalenwand in Zylinder–
mitte beträgt p 3 = γ ⋅ Z / 2 = 12 ⋅ 5 = 60. kN/m 2 , so daß sich der Wert der Ringkraft zu
n 11 = p 3 ⋅ R = 60 ⋅ 5 = 300. kN/m berechnet, der mit dem Wert im (Bild 1.4.3a) übereinstimmt.
Im gestörten unteren Zylinderbereich gilt die Faßformel nicht mehr. Vorzeichen und
Verlauf der Ringkraft weichen daher erheblich vom Verlauf in Zylindermitte ab. Eine
analytische Berechnung ist kaum möglich. Dies trifft neben der Meridiankraft n 22 im
(Bild 1.4.3b) auch für die Momente m 11 und m 22 zu. Sie sind in den (Bildern 1.4.4a
und b) dargestellt und geben den Plattenanteil der Schalenlösung an. Die Ringmomente
m 11 im (Bild 1.4.4a) fallen insgesamt sehr klein aus und werden in analytischen
Betrachtungen i.a. vernachlässigt. Das Meridianmoment im (Bild 1.4.4b) ist im ungestörten
Bereich ebenfalls vernachlässigbar klein, im gestörten Bereich aber von dominanter
Größenordnung.
Es sind elementare Kenntnisse aus der Schalentheorie erforderlich, um das Tragverhalten
von aus Teilschalen zusammengesetzten Behältern genauer zu verstehen. Da
sie noch nicht vorliegen, sondern erst im Rahmen der Lehrveranstaltung Statik IV erarbeitet
werden sollen, ist eine weitere Diskussion an dieser Stelle nicht sinnvoll.
– 1 / 27 –

4.50+02
3.00+02
1.50+02
0.
–1.50+02
–3.00+02
–4.50+02
a) Ringkraft
3.00+02
1.50+02
0.
–1.50+02
–3.00+02
–4.50+02
–6.00+02
b) Meridiankraft
n 11 (kN�m)
–1.80+02 –1.20+02 –6.00+01 0. 6.00+01 1.20+02 1.80+02
n 22 (kN�m)
–1.80+02 –1.20+02 –6.00+01 0. 6.00+01 1.20+02 1.80+02
Bild 1.4.3 : Behälter: Membrankräfte in Ringschnitten
– 1 / 28 –
Mitte Zylinder
Unteres Ende Zylinder
� 1 (Grad)
� 1 (Grad)

3.00–01
1.50–01
0.
–1.50–01
–3.00–01
–4.50–01
–6.00–01
–1.80+02 –1.20+02 –6.00+01 0. 6.00+01 1.20+02 1.80+02
a) Ringmoment
3.00–01
0.
–3.00–01
–6.00–01
–9.00–01
–1.20+00
–1.50+00
m 11 (kNm�m)
m 22 (kNm�m)
–1.80+02 –1.20+02 –6.00+01 0. 6.00+01 1.20+02 1.80+02
b) Meridianmoment
Bild 1.4.4 : Behälter. Biegemomente in Ringschnitten
– 1 / 29 –
Mitte Zylinder
Unteres Ende Zylinder
� 1 (Grad)
� 1 (Grad)

1.5.4 Faltwerk
Die dichte Bebauung in innerstädtischen Lagen hat vielfach zur Folge, daß die Außenkanten
von benachbarten Bauwerken auf den Grundstücksgrenzen zusammenstoßen.
Eine mittige Gründung von tragenden Außenwänden und von Stützen, die in den Fluchten
der Außenwände liegen, ist dann nicht mehr möglich. Bei halbseitigen Gründungen
mit notwendigerweise exzentrischer Lasteinleitung entstehen aber große Versatzmomente.
Es sind daher in der Regel Sonderüberlegungen anzustellen, um diese zusätz–
lichen Versatzmomente aufzunehmen. Eine häufig angewandte konstruktive Lösung
besteht darin, Zentrierbalken anzuordnen, um die Versatzmomente in Kräftepaare zu
überführen.
Im (Bild 1.5) ist ein Ausschnitt aus dem Gründungstragwerk eines Warenhauses dargestellt.
Die Flachgründung wird in Stahlbeton errichtet und vor Ort betoniert. Sie besteht
aus einer unmittelbar auf dem Baugrund aufliegenden Bodenplatte und aus Kellerwänden,
die als massive Wandscheiben zusammen mit der Bodenplatte ein dehn– und biegesteifes
Faltwerk bilden. Die Bodenplatte ist in den Schnittpunkten des Stützenrasters
durch Einzelfundamente verstärkt, um die Stützenlasten aufzunehmen, vgl. (Bild 1.5).
Im Randbereich können die Einzelfundamente wegen der Randbebauung nur halbseitig
ausgeführt werden. Durch die ungewollte Exzentrizität erhalten die Stützen und angrenzenden
Kellerwände an der Außenseite eine große Beanspruchung aus Biegezug,
die u.a. das Dichtungskonzept der geplanten weißen Wanne in Frage stellt. Dieser Zusammenhang
ist in der nachfolgenden Skizze verdeutlicht.
Einwirkung Randstütze
Halbseitiges
Einzelfundament
Resultierende
Bodenpressung
Grundstücksgrenze
– 1 / 30 –
+
M = N R ⋅ e
N R
+
Große Zug–
beanspruchung
in der Kellerwand !
e
N R

150 kN/m
6.00
0.775
16.325
11.125
6000 kN
Kellerwand
t = 0.45 m
2.60
Bild 1.5 : Faltwerk
5.50
1250 kN
2.60
1.80 6.60
Grundstücksgrenze
X 3 (Z)
X 1 (X)
1.50
5.50
5350 kN
X 2 (Y)
1.50
225 kN
11300 kN
2.00 2.00
Symmetrie–
linie X 1 = konst.
Gründung
Baugrund
– 1 / 31 –
15.725 m
11.225 4.50
Kellerwand
t = 0.45 m
Grundstücksgrenze
1.50
2.55
3.00 3.00
1.50
3.20
8120 kN
6.35
2.00
2.00
80 kN/m
6.00
0.775
2.00
Symmetrie–
linie X 2 = konst.
Einzelfundamente mit
Zentrierbalken t = 1.50 m
Bodenplatte t = 0.40 m
: Stahlbeton, E = 3 ⋅ 10
: Bodengutachten
7 kN/m2 ,
, E = 5 ⋅ 104 kN/m2 ν = 0.2.
,
ν = 0.35.

Es ist daher vorgesehen, Randstützen und Kellerwände mit Hilfe von Zentrierbalken zu
entlasten, vgl. (Bild 1.5). Und zwar so, daß ein großer Anteil des Versatzmomentes als
vertikale Zugkraft auf das benachbarte Mittelfundament einwirkt. Dieser Zusammenhang
ist in der nachfolgenden Skizze verdeutlicht.
Einwirkung Randstütze
Zentrierbalken
Resultierende
Bodenpressung
Grundstücksgrenze
Einwirkung
Mittelstütze
– 1 / 32 –
+
M ≈ 0
N R
Geringe Zug–
beanspruchung
in der Kellerwand !
Die Frage, ob diese einfache statische Modellbildung ausreicht, um die wirklichen Verhältnisse
in einer räumlichen Kellerecke wirklichkeitsnah zu erfassen, bleibt allerdings
offen. Sie läßt sich nur durch eine Untersuchung mit Hilfe der FEM beantworten. Dazu
ist der Ausschnitt gemäß (Bild 1.5) mit Scheiben– und Plattenelementen zu elementieren
und mit den vorgegebenen Einwirkungen und Materialdaten als Faltwerk zu berechnen.
Zur Beurteilung der Ergebnisse ist es wichtig zu wissen, wie sich die Bodenpressung
im Baugrund einstellt. Er wurde daher mit Volumenelementen elementiert, um u.a.
auch den Einfluß der Setzungsmulde zu erfassen. Die Elementierung des Baugrunds
und des Faltwerks im verformten Zustand sind im (Bild 1.5.1) dargestellt und die Verteilung
der Bodenpressung σ 33 (kN/m 2 ) des Baugrunds im (Bild 1.5.2). Das Mittelfundament
erhält mit 11300 kN die mit Abstand größte Auflast. Die Bodenpressung unter
+
N RD
–
N RZ

– 1 / 33 –
X
Z
Y
Bild 1.5.1 : Faltwerk–Baugrund. Resultierende Verschiebung

– 1 / 34 –
X
Z
Y
Bild 1.5.2 : Vertikale Spannungsverteilung σ 33 (kN/m
2
) im Baugrund (Z–Richtung)
1.31+01
–1.84+01
–4.99+01
–8.14+01
–1.13+02
–1.44+02
–1.76+02
–2.07+02
–2.39+02
–2.70+02
–3.02+02
–3.34+02

dem Fundament ist aber erheblich kleiner als unter den Randstützen, die deutlich geringere
Auflasten erhalten. Dies ist als Hinweis zu werten, daß die Zentrierbalken wie vorgesehen
statisch wirken, da sie ins Mittelfundament Zugkräfte einleiten, die zur Verringerung
der dort wirkenden Stützenauflast beitragen und somit die Bodenpressung
reduzieren.
In den (Bildern 1.5.3 und 1.5.4) ist die Verteilung der Scheibenkräfte n 11 (kN/m) und
n 22 (kN/m) in den Kellerwänden und der Bodenplatte dargestellt. Sie stimmen mit den
Erwartungen überein. In den Kellerwänden stellen sich z.B. Druckzwiebeln unter den
Einzellasten ein und in der Bodenplatte steigen im Bereich der Zentrierbalken die Scheibenkräfte
an, weil wegen der unterschiedlichen Dicken zwischen Platte und Balken eine
Dehnungsbehinderung auftritt. Auch die Zugkräfte im oberen Kellerwandbereich, die
sich zwischen den Stützenauflasten einstellen, sind als Spaltzugkräfte charakteristisch
für das Tragverhalten von Scheiben, vgl. (Bild 1.5.4).
Interessant ist, daß im unteren Eckbereich der Kellerwände Zugkräfte auftreten,
vgl. (Bild 1.5.3). Sie resultieren aus der Eckverankerung der Bodenplatte, die dort
durch die Wirkung der Bodenpressung von den stützenden Scheibenrändern abhe–
ben will, wegen der Verankerung aber nicht kann und daher eine Verankerungskraft in
die Kellerwand–Scheiben einleitet. Dieser Effekt, in der Literatur unter dem Namen
Kirchhoff’sche Eckkraft bekannt, ist u.a. Gegenstand von theoretischen Betrachtungen,
die im Rahmen der Lehrveranstaltung Statik IV zur Plattentheorie durchgeführt werden.
1.6 Erkenntnisse
Die präsentierten Anwendungsbeispiele verdeutlichen den hohen Entwicklungsstand
von rechnerorientierten Methoden in der Baustatik. Besonders bei Flächentragwerken
erleichtert die grafische Auswertung der Ergebnisse in Form von farbig *) angelegten
Höhenstreifen oder Trajektoren die Interpretation und damit die Einsicht in das Tragverhalten.
Es bleibt aber anzumerken, daß die Handhabung von verfügbaren Programmen
allein nicht ausreicht, um mit dieser Technik auch baustatische Qualität zu erzeugen.
Das ist nur möglich, wenn vor allem die baustatischen Theorien, die den Berechnungen
zugrunde liegen, voll verstanden werden. Ist dies nicht der Fall, entfällt die Möglichkeit
zur Kontrolle der erzielten Ergebnisse. Sie ist aber unabdingbar, da sich vor allem bei
größeren Anwendungsbeispielen eine Vielzahl von Fehlerquellen ergeben, die es im
Rahmen einer baustatischen Ergebnisinterpretation einzugrenzen gilt.
*) Im Skript wird auf eine farbige Darstellung verzichtet, um die Reproduktionskosten zu verringern.
– 1 / 35 –

– 1 / 36 –
X
Z
Y
Bild 1.5.3 : Verteilung von n 11 (kN/n) im Faltwerk,
Kellerwände: Z–Richtung; Bodenplatte: Y–Richtung
6.12+02
1.51+02
–3.10+02
–7.71+02
–1.23+03
–1.69+03
–2.15+03
–2.61+03
–3.08+03
–3.54+03
–4.00+03
–4.46+03
–4.92+03
–5.38+03
–5.84+03
–6.30+03

– 1 / 37 –
Z
2
X
X
Z
Y
Bild 1.5.4 : Verteilung von n 22 (kN/m) im Faltwerk, Kellerwände: X– bzw. Y–Richtung, Bodenplatte: X–Richtung
1.41+03
1.20+03
9.93+02
7.83+02
5.73+02
3.64+02
1.54+02
–5.61+01
–2.66+02
–4.76+02
–6.86+02
–8.95+02
–1.11+03
–1.31+03
–1.52+03
–1.73+03

Teil 2: Bezeichnungen
2.1 Indexschreibweise
Im Rahmen der Lehrveranstaltung Statik IV wird konsequent die Indexschreibweise
angewendet. Sie beschreibt baustatische Zusammenhänge mit Hilfe von indizierten
Größen. Dabei ist wie gewohnt zwischen Geometrie–, Einwirkungs– und Zustands–
größen zu unterscheiden. Diese Größen sind für den allgemeinen Fall eines dreidimensionalen
Kontinuums im (Bild 2.1) dargestellt. Sie sind in geeigneter Weise auf flächenbezogene
Größen zu reduzieren, um Berechnungstheorien für Flächentragwerke
abzuleiten. Dies geschieht im einzelnen in den Teilen 3 bis 5, die sich mit den Grund–
lagen der Scheiben–, Platten– und Schalentheorie beschäftigen. Zuvor sollen wesent–
liche Merkmale der Indexschreibweise erklärt werden, ohne Anspruch auf Vollständigkeit
zu erheben.
Indizes von indizierten Größen, die sich auf räumliche Gegebenheiten gemäß (Bild 2.1)
beziehen, werden durch kleine lateinische Buchstaben gekennzeichnet. Sie durch–
laufen grundsätzlich den Wertebereich von 1 bis 3.
i, j, k ... � 1, 2, 3
– 2 / 1 –
(2.1)
Beziehen sich die indizierten Größen dagegen auf Flächentragwerke, erfolgt die Kennzeichnung
mit kleinen Buchstaben des griechischen Alphabets, die nun den Werte–
bereich von 1 bis 2 durchlaufen.
�, �, � ... � 1, 2
(2.2)
Stellung und Reihenfolge von Indizes sind nicht willkürlich, sondern beschreiben
spezielle Eigenschaften der indizierten Größen. Sie sind vorab festzulegen und danach
im Rahmen der Anwendung streng zu beachten. So hat es sich z.B. als sinnvoll er–
wiesen, Wegzustände immer unten und Kraftzustände immer oben zu indizieren.
Weiter gelten die Regeln, daß indexfreie Größen Skalare sind, daß der Index von einfach
indizierten Größen immer die Richtung angibt und daß bei einem Indexpaar der
erste Index den Ortsbezug und der zweite Index den Richtungsbezug ausdrückt. Lediglich
bei geometrischen Größen ist eine freiere Indizierung erlaubt. So werden z.B. Koordinaten
in der Regel oben, Längen und Flächen i.a. aber unten indiziert.

Θ 3 , f 3 , v 3
Körperfeste
Koordinaten
X 1
A 3
R
σ 33 ,ε 33
σ 32 ,ε 32
σ 31 ,ε 31
L 1
X 3
Θ 1 , f 1 , v 1
Bild 2.1 : Ausschnitt aus einem Kontinuum
σ 23 ,ε 23
L 2
X 2
Ortsfeste Koordinaten
– 2 / 2 –
A 2
σ 22 ,ε 22
σ 21 ,ε 21
σ 13 ,ε 13
A 1
σ 12 ,ε 12
σ 11 ,ε 11
L 3
Θ 2 , f 2 , v 2

2.2 Geometrische Größen
Zur geometrischen Beschreibung von Tragwerken sind globale und lokale Koordinatensysteme
einzuführen. Globale Systeme sind im dreidimensionalen Euklid–Raum E3
definiert.
X � �X 1 ,X 2 ,X 3� � �X i�.
– 2 / 3 –
(2.3)
Sie sind ortsfest und kartesisch (Bild 2.1). Lokale Systeme sind dagegen immer körperfest.
Für den allgemeinsten Fall sind sie im dreidimensionalen gekrümmten Riemann–
Raum R3 definiert.
� � �� 1 , � 2 , � 3� � �� i�.
(2.4)
Der Riemann–Raum ist eine mathematische Definition. Ein anschaulicher Zusammenhang
mit unserem Erfahrungsraum, nämlich den Euklid–Raum, ist somit nicht unmittelbar
gegeben.
Lokale Systeme sind in der Regel krummlinig und schiefwinklig (Bild 2.1). Sie können
aber auch kartesisch sein. Dann fällt der R3– mit dem E3–Raum zusammen. Bei numerischen
Tragwerksberechnungen ist man daher stets bemüht, diesen Zustand zu erreichen,
was bis auf Schalen i.a. auch immer gelingt.
Der Zusammenhang zwischen globalem und lokalem System ist durch die Parame–
terabbildung
R � R �X i �� i��
(2.5)
gegeben, die aus geometrischer Sicht einen Ortsvektor darstellt, vgl. (Bild 2.1). Für die
baustatische Beschreibung ist das körperfeste System Gl. (2.5) von entscheidender Bedeutung,
da es als lokales System vorrangig die physikalischen Eigenschaften eines
Tragwerks erfaßt. Das ortsfeste System Gl. (2.4) dient vor allem als Bezugssystem. Es
ist immer dann erforderlich, wenn das betrachtete Gesamttragwerk aus räumlich
angeordneten Einzeltragwerken besteht, wenn z.B. räumlich angeordnete Scheiben
und Platten ein Faltwerk bilden, vgl. (Bild 1.5). Bei einzelnen Scheiben (vgl. Bild 1.2)
und Platten (vgl. Bild 1.3) ist eine Unterscheidung zwischen orts– und körperfestem
System i.a. nicht erforderlich, so daß in diesen Fällen beide Systeme zusammenfallen,
vgl. Teil 3 und 4.
Längenmessungen sind in Richtung der körperfesten Koordinaten Θ i vorzunehmen.
Es gilt
L � �L 1 ,L 2 ,L 3 � � �L i � .
(2.6)

Schnittflächen im dreidimensionalen Kontinuum sind durch Schnitte Θ i = konstant
definiert.
A � �A 1 ,A 2 ,A 3 � � �A i � .
Im einzelnen gilt
und
A 1 � A 1 �� 1 � konstant, � 2 , � 3� ,
A 2 � A 2 �� 1 , � 2 � konstant, � 3�
A 3 � A 3 �� 1 , � 2 , � 3 � konstant� .
– 2 / 4 –
(2.7)
(2.7.1)
(2.7.2)
(2.7.3)
Die Schnittflächen Gl. (2.7) werden vielfach auch als Spannungsflächen bezeichnet,
weil sie u.a. dazu dienen, den Wirkungsort von Spannungen zu definieren.
2.3 Einwirkungsgrößen
Als äußere Größen können sowohl Weg– als auch Kraftzustände auf das zu unter–
suchende Tragwerk einwirken. Hier werden stellvertretend für beliebige Einwirkungen
lediglich volumenbezogene Krafteinwirkungen betrachtet. Sie greifen jeweils in Richtung
einer körperfesten Koordinate an und sind für den allgemeinsten Fall als Funktion
aller körperfesten Koordinaten zu definieren. Es gilt
f �
f 1 �� 1 , � 2 , � 3�
f 2 �� 1 , � 2 , � 3�
f 3 �� 1 , � 2 , � 3�
= f i �� j� .
(2.8)
Die Überstreichung der Größen soll darauf hinweisen, daß es sich um vorgegebene,
also bekannte Größen, handelt, die sich im Verlauf der Berechnung nicht verändern. Die
Vorgabe von Gl. (2.8), z.B. als spezifisches Gewicht hat in der Dimension kN/m 3 oder
N/mm 3 zu erfolgen.

2.4 Zustandsgrößen
Gesucht sind diejenigen Weg– und Kraftzustände, die sich einstellen, wenn z.B. volumenbezogene
Lasten Gl. (2.8) auf ein dreidimensionales Tragwerk mit Abmessungen
Gl. (2.6) einwirken, vgl. (Bild 2.1). Als äußere Weggrößen sind Verschiebungen in Richtung
der körperfesten Koordinaten zu ermitteln. Sie sind als Funktion aller körperfesten
Koordninaten definiert, treten in der Dimension (m) oder (mm) auf und bilden mit den
äußeren Kraftgrößen der Einwirkungen Gl. (2.8) arbeitskonforme Paare. Es gilt
v �
v 1 �� 1 , � 2 , � 3�
v 2 �� 1 , � 2 , � 3�
v 3 �� 1 , � 2 , � 3�
= v i �� j� .
– 2 / 5 –
(2.9)
Als innere Kraftgrößen sind Spannungen in den Schnittflächen Gl. (2.7) zu ermitteln. Sie
sind als Funktion der körperfesten Koordinaten definiert und treten in der Dimension
(kN/m 2 ) oder (N/mm 2 ) auf. In jeder Schnittfläche (erster Index) sind Spannungen in
drei Richtungen (zweiter Index) zu beachten, so daß sich bei drei Schnittflächen insgesamt
neun Spannungskomponenten ergeben. Es gilt
� �
� 11�� 1 , � 2 , � 3�
� 12�� 1 , � 2 , � 3� � 13�� 1 , � 2 , � 3�
� 21�� 1 , � 2 , � 3� � 22�� 1 , � 2 , � 3� � 23�� 1 , � 2 , � 3�
� 31�� 1 , � 2 , � 3� � 32�� 1 , � 2 , � 3� � 33�� 1 , � 2 , � 3�
= �ij��k� .
(2.10)
Die Verschiebungen Gl. (2.9) und die Spannungen Gl. (2.10) sind Bemessungsgrößen,
um die Gebrauchstauglichkeit und die Tragfähigkeit von Bauwerken nachzuweisen.
Innere Weggrößen haben dagegen den Charakter von Hilfsgrößen. Sie werden ausschließlich
zur Bestimmung der Bemessungsgrößen benötigt, sind als Verzerrungen in
Abhängigkeit der körperfesten Koordinaten definiert und bilden mit den Spannungen
Gl. (2.10) arbeitskonforme Paare. In jeder Schnittfläche (erster Index) treten Verzerrungen
in drei Richtungen (zweiter Index) auf, so daß sich bei drei Schnittflächen insgesamt
neun Verzerrungskomponenten ergeben. Es gilt
� �
� 11 �� 1 , � 2 , � 3�
� 12 �� 1 , � 2 , � 3� � 13 �� 1 , � 2 , � 3�
� 21 �� 1 , � 2 , � 3� � 22 �� 1 , � 2 , � 3� � 23 �� 1 , � 2 , � 3�
� 31 �� 1 , � 2 , � 3� � 32 �� 1 , � 2 , � 3� � 33 �� 1 , � 2 , � 3�
= � ij �� k�
.
(2.11)

2.5 Arbeitskonforme Größen
Die Arbeitsgleichung
W v � W v a � W v i
� 0
– 2 / 6 –
(2.12)
ist von zentraler Bedeutung für die gesamte Baustatik. In Gl. (2.12) werden virtuelle Arbeiten
(oberer Index v) bilanziert, die sich aus äußeren (unterer Index a) und inneren
Anteilen (unterer Index i) zusammensetzen. Das PvW und das PvK sind aus der Statik
für Stabtragwerke bekannt. Sie sind aber auch hervorragend geeignet, um Näherungslösungen
für Flächentragwerke zu ermitteln. Zur Formulierung von virtuellen Arbeitsprinzipien
ist es erforderlich, arbeitskonforme Paare zu bilden. Dies ist nur mit arbeitskonformen
Größen möglich. Hierunter versteht man einander zugeordnete Weg– und
Kraftgrößen, deren Produkte virtuelle Arbeitsausdrücke in der Dimension (kN ⋅ m) oder
(N ⋅ mm) ergeben.
Besteht die Zuordnung aus virtuellen Weggrößen (oberer Index v) und wirklichen Kraftgrößen,
bezeichnet man die Produkte als virtuelle Weggrößenarbeit. Auf dieser Formulierung
beruht das PvW. Die äußere Weggrößenarbeit ist durch den Ausdruck
W v a �� v
�v v 1 f 1 � v v 2 f 2 � v v 3 f 3 �dV �� v
v v i f i dV
definiert und die innere Weggrößenarbeit durch den Ausdruck
� W v i �� v
(� v 11 �11 � � v 12 �12 � � v 13 �13
� � v 21 �21 � � v 22 �22 � � v 23 �23
� � v 31 �31 � � v 32 �32 � � v 33 �33 ) dV �� v
� v ij �ij dV.
(2.13.1)
(2.13.2)
Besteht die Zuordnung dagegen aus virtuellen Kraftgrößen (unterer Index v) und wirk–
lichen Weggrößen, bezeichnet man die Produkte als virtuelle Kraftgrößenarbeit. Auf
dieser Formulierung beruht das PvK. Im Fall von volumenbezogenen Krafteinwirkungen
verschwindet die äußere Kraftgrößenarbeit.
W v a � 0. (2.14.1)

Eine Definition ergibt keinen Sinn, da die äußeren Kraftgrößen Gl. (2.8) Einwirkungen
sind, die sich als vorgeschriebene Größen nicht ändern, so daß keine äußeren virtuellen
Kraftgrößen auftreten können. Die innere Kraftgrößenarbeit ist durch den Ausdruck
� W v i �� v
(� 11
v � 11 � � 12
v � 12 � � 13
v � 13
� � 21
v � 21 � � 22
v � 22 � � 23
v � 23
� � 31
v � 31 � � 32
v � 32 � � 33
v � 33 � dV �� v
– 2 / 7 –
� ij v � ij dV
(2.14.2)
definiert. Die Integration in Gl. (2.13) und Gl. (2.14) ist jeweils über das Volumen des
betrachteten Kontinuums zu führen.
Bei der Bildung der Kurzformen von Gl. (2.13) und Gl. (2.14) ist eine zusätzliche Regel
zu beachten, um die Summation der einzelnen Arbeitsanteile zu erfassen. Sie wird als
Summationsregel bezeichnet.
Summationsregel:
Sind in Formeln oder sonstigen Ausdrücken indizierte Größen enthalten, die unten
und oben gleiche Indizes aufweisen, so ist über alle Zahlenwerte zu summieren,
die von den betreffenden Indizes in Abhängigkeit vom definierten Wertebereich
Gl. (2.1) bzw. Gl. (2.2) durchlaufen werden.
Die mathematische Art der Formeln und Ausdrücke ist beliebig. Zur Summation können
Einzelgrößen, Ableitungsgrößen, Produkte, Quotienten oder gemischte Formeln und
Ausdrücke anstehen. Die Indizierung muß aber eindeutig sein. Formeln und Ausdrücke,
in denen der gleiche Index mehr als zweimal Verwendung findet, ergeben keinen Sinn
und sind daher als falsch einzuordnen.
Die Summationsregel führt im Rahmen der Indexschreibweise zu sehr kompakten Ausdrücken
im Formelapparat. Darüber hinaus erlaubt sie eine physikalische Interpretation
der dargestellten Größen. Arbeitsausdrücke sind z.B. Skalare. Die Indizes in Gl. (2.13)
und Gl. (2.14) heben sich durch die Summation auf und haben somit keine Wirkung
nach außen. Sie werden daher auch als stille Indizes bezeichnet. An den verbleibenden
Indizes kann man also sofort erkennen, um was für eine physikalische Größe es sich
handelt: Heben sich die Indizes vollständig auf, liegt ein Skalar vor. Verbleibt ein Index
unten, liegt eine Verschiebungskomponente gemäß Gl. (2.9) vor. Steht der Index oben,
muß es sich um eine äußere Kraftgröße handeln, z.B. um eine volumenbezogene Einwirkung
gemäß Gl. (2.8). Verbleibt dagegen ein Indexpaar, muß es oben stehen, da es
sich bei der indizierten Größe zwangsläufig um eine Spannung bzw. Schnittgröße handeln
muß.

Teil 3: Scheibentheorie
3.1 Einführung
Die Scheibentheorie beschreibt das baustatische Verhalten von ebenen Flächentragwerken,
bei denen die Lastebene mit der Mittelfläche des dünnwandigen Tragwerks zusammenfällt.
Ziel ist es, zweidimensionale Weg– und Kraftgrößen zu definieren und zu
berechnen, die sich aus den allgemeinen dreidimensionalen Kontinuumsgrößen ergeben,
wenn man die geometrischen und physikalischen Voraussetzungen beachtet, die
Scheibentragwerke charakterisieren. Diese Größen erfassen den Beanspruchungszustand
mit ausreichender Genauigkeit, um Scheibentragwerke sicher und wirtschaftlich
planen und bemessen zu können, vgl. z.B. Einführungsbeispiel 1.5.1: Wandscheibe. Im
Rahmen der Scheibentheorie sind die Problemstellung zu formulieren, die Grundgleichungen:
Gleichgewicht und Verträglichkeit abzuleiten, allgemeine Lösungswege aufzuzeigen
und spezielle Lösungsmethoden zu entwickeln. Dies geschieht in den Abschnitten
3.2 bis 3.6. Ein Zahlenbeispiel im Abschnitt 3.7, das mit dem baustatischen
Verfahren von Schleeh /6/ berechnet wird, beschließt die Ausführungen zur Scheiben–
theorie.
3.2 Voraussetzungen der Scheibentheorie
Ein rechteckig begrenzter Ausschnitt aus einem dreidimensionalen Scheibenkontinuum
ist im (Bild 3.1) dargestellt.
L 2 = H
X 3
f 3 ,v 3
X 2
f 2 ,v 2
Bild 3.1 : Scheibenkontinuum
A 2
A 2
σ 3j ,ε 3j
σ 2j ,ε 2j
A 3
L 1 = L
A 1
– 3 / 1 –
n22 p
,α22 2 ,u2; n 21 ,α 21
σ 1j ,ε 1j
Mittelfläche
Kontinuums–
größen
A 3
Scheibengrößen
n 12 ,α 12
n11 p
,α11 A1 1 ,u1; L 3 = t
X 1
f 1 ,v 1

Zur geometrischen Beschreibung werden die kartesischen Koordinaten X 1 und X 2
eingeführt, die als ortsfeste Koordinaten die Mittelfläche der Scheibe aufspannen. Die
Betrachtung ist auf eine einzelne Scheibe beschränkt. Die ortsfesten Koordinaten stimmen
daher mit den körperfesten Koordinaten überein. Es gilt: Θ 1 ≡ X 1 und Θ 2 ≡ X 2 .
Die Koordinate Θ 3 ≡ X 3 , die in Richtung der Dicke der Scheibe zeigt, steht senkrecht
zur Mittelfläche.
Für die Abmessungen des baustatischen Modells Scheibe gilt die geometrische Restriktion
(L 1 � L, L 2 � H) �� (L 3 � t) . (3.1)
Nach Gl. (3.1) muß die Längen (L)– und die Höhenabmessung (H) deutlich größer sein
als die Dicke (t), so daß die dritte Koordinate X 3 als unabhängige Beschreibungskoordinate
entfällt. Die Berechnung kann dann mit den im (Bild 3.1) dargestellten Scheibengrößen
der Mittelfläche durchgeführt werden. Ab dem Verhältnis
L : H � 4 : 1 (3.2)
gilt die Stabwerkstheorie, weil dann die Dehnung im Scheibenquerschnitt in guter Näherung
linear verteilt ist (Hypothese vom Ebenbleiben der Querschnitte oder Hypthese
von Bernoulli), so daß auch die zweite Koordinate X 2 entfällt.
Die volumenbezogenen Kräfte f i , die z.B. in der Dimension (kN/m 3 ) auf das dreidimensionale
Scheibenkontinuum einwirken, sind auf die Mittelfläche zu reduzieren. Mit der
Restriktion
f 3 � 0 (3.3)
erhält man als flächenbezogene Scheibeneinwirkung den Integralausdruck
p � �� t
f � dX 3 . (3.4)
Die Flächenlasten Gl. (3.4), die z.B. in der Dimension (kN/m 2 ) anzugeben sind, wirken
in der Mittelfläche in Richtung der X 1 – und X 2 –Koordinaten. Anzumerken ist, das Flächenlasten
bei realen Scheibenproblemen selten auftreten. Typische Lastfälle sind Einzellasten
oder Linienlasten, die auf den Rändern oder im Inneren der Scheibe angreifen,
vgl. (Bild 1.2). Im Rahmen der vorliegenden Betrachtung ist Gl. (3.4) daher als
stellvertretender Lastfall anzusehen, um eine vollständige Theorie zu entwickeln. Für
andere Lastfälle ergeben sich äquivalente Zusammenhänge.
Zusätzlich zur Festlegung der Geometrie und Einwirkung ist noch der Beanspruchungszustand
zu definieren, der sich in Scheiben einstellen kann. Es ist ein reiner Dehnungszustand.
Dabei ist zwischen ebenem Spannungs– und ebenem Verformungszustand
zu unterscheiden, je nach dem, welche Randbedingungen auf den Spannungsflächen
A 3 vorliegen, die das Scheibenkontinuum in Richtung der X 3 –Koordinate nach außen
begrenzen.
– 3 / 2 –

Ein ebener Spannungszustand liegt vor, wenn auf den Spannungsflächen A 3 des
Scheibenkontinuums (Bild 3.1) keine Spannungen auftreten, so daß sich als Reaktion
darauf die Begrenzungsflächen der Scheibe frei verformen können.
A 3 : � 3j � 0 � � 3j � 0. (3.5)
Gl. (3.5) ist z.B. für den wichtigen Fall der Wandscheiben erfüllt. Im konstruktiven
Ingenieurbau ist der ebene Spannungszustand daher als Regelfall anzusehen. Wegen
Gl. (3.3) und Gl. (3.5) gilt zusätzlich in der Spannungsfläche A 1 die Bedingung σ 13 = 0
und in der Spannungsfläche A 2 die Bedingung σ 23 = 0.
Ein ebener Verformungszustand liegt vor, wenn die Spannungsflächen A 3 des Scheibenkontinuums
sich nicht verformen können, so daß als Reaktion darauf Spannungen
auftreten.
A 3 : � 3j � 0 � � 3j � 0. (3.6)
Gl. (3.6) ist erfüllt, wenn man z.B. Wellen in Längsrichtung in Kreisscheiben der
Dicke t zerlegt, zwischen denen die Spannung σ 33 wirkt (Bild 3.2). Dieser Fall ist für
den konstruktiven Ingenieurbau aber von untergeordneter Bedeutung. Er wird daher
nicht weiter behandelt.
X 2
X 1
Kreisscheibe
Bild 3.2 : Scheibenmodell einer Welle
Achse
– 3 / 3 –
A 3
σ 33
3.3 Berechnungsgrößen der Scheibentheorie
Im Scheibenkontinuum (Bild 3.3) können sich die Verschiebungen v 1, v 2 und v 3
einstellen. Wegen der Restriktion Gl. (3.3) gilt aber v 3 ≡ 0. Die Lastebene von Schei–
benproblemen fällt mit der Mittelfläche des Scheibenkontinuums zusammen, in der die
Verschiebungen u 1 und u 2 auftreten. Sie stimmen mit den Verschiebungen v 1 und
v 2 überein und verhalten sich arbeitskonform zur Flächenlast Gl. (3.4). Es gilt
v��X � ,X 3� � u�(X � ) . (3.7)
t
X 1
X 3
σ 33
A 3

Bei Annahme eines ebenen Spannungszustandes Gl. (3.5) wirken in der Spannungs–
fläche A 1 die Spannungen σ 11 und σ 12 und in der Spannungsfläche A 2 die Spannungen
σ 21 und σ 22 . Dazu gehören die arbeitskonformen Dehnungen ε 11 und ε 12 bzw.
ε 21 und ε 12. Die gleichwertigen Kraft– und Weggrößen der Mittelfläche sind durch die
resultierenden Spannungen
n �� �� t
� �� dX 3
und die Dehnungen
� �� �X � ,X 3� � � �� (X � )
definiert, die sich ebenfalls arbeitskonform zueinander verhalten.
– 3 / 4 –
(3.8)
(3.9)
Die Scheibenkräfte Gl. (3.8) sind längenabhängige Größen. In der Spannungsfläche
A 1 mit X 1 = konstant bezieht sich die Längenabhängigkeit auf die X 2 –Koordinate
und in der Spannungsfläche A 2 mit X 2 = konstant auf die X 1 –Koordinate. Die Angabe
kann z.B. in der Dimension (kN/m) erfolgen. Die Dehnungen Gl. (3.9) haben dagegen
lediglich die Bedeutung von Hilfsgrößen, um die Scheibenkräfte zu berechnen.
Mit Gl. (3.4), Gl. (3.7), Gl. (3.8) und Gl. (3.9) sind alle Einwirkungs– und Berechnungsgrößen
der Scheibentheorie definiert. Die arbeitskonforme Zuordnung ist im (Bild 3.3)
dargestellt, vgl. auch (Bild 3.1).
p 2 ,u 2
X 2
A 2
Mittelfläche
n 22 ,α 22
A 1
n 21 ,α 21
n 12 ,α 12
n 11 ,α 11
Bild 3.3 : Einwirkungs– und Berechnungsgrößen der Scheibentheorie
t
2
t
t
2
Mittelfläche
X 1
p 1 ,u 1

Bei Vorgabe der Einwirkungen p α sind zu berechnen:
– Zum Nachweis der Tragfähigkeit die Scheibenkräfte n αβ = n βα .
– Zum Nachweis der Gebrauchstauglichkeit die Verschiebungen uα .
Dazu sind die Grundgleichungen für das Gleichgewicht und die Verträglichkeit aufzustellen
und analytisch oder numerisch zu lösen.
3.4 Grundgleichungen der Scheibentheorie
3.4.1 Gleichgewicht
Das Gleichgewicht der Scheibenkräfte ist am Flächenschnitt (Bild 3.4) zu formulieren.
Im Rahmen der Theorie I. Ordnung geschieht dies näherungsweise am unverformten
System. Zwischen linker und rechter Spannungsfläche A 1 nimmt die Koordinate X 1
um die Strecke ∆X 1 zu und zwischen unterer und oberer Spannungsfläche A 2 die Koordinate
X 2 um die Strecke ∆X 2 . In dem Flächenelement ∆X 1 ⋅∆X 2 wirken die Flächenlasten
p 1 und p 2 . Dadurch ändern sich in der Spannungsfläche A 1 die Scheibenkräfte
n 11 um den Betrag ∆n 11 und n 12 um den Betrag ∆n 12 und in der Spannungsfläche
A 2 die Scheibenkräfte n 21 um den Betrag ∆n 21 und n 22 um den Betrag ∆n 22 . Alle
Größen sind auf die ortsfesten Koordinaten X 1 und X 2 bezogen. Richtungsänderungen
treten daher nicht auf.
X 2 ,A 2
oben A 2
n 11
n 12
links A 1
∆X 2
n 21
Positive Drehung
um die Scheibennormale
Bild 3.4 : Flächenschnitt Scheibentragwerk
– 3 / 5 –
n 22 +∆n 22
n 21 +∆n 21
p 2
∆X 1
p 1
n 22
n 12 +∆n 12
n 11 +∆n 11
unten A 2
rechts A 1
X 1 ,A 1
Das Kräftegleichgewicht ist in Richtung der X 1 – und X 2 –Koordinaten zu erfüllen und
das Momentengleichgewicht um die Scheibennormale, die senkrecht auf der (X 1 –
X 2 )–Fläche steht und mit der X 3 –Koordinaten zusammenfällt, vgl. (Bild 3.1). Dabei ist
der Mittelwertsatz der Integralrechnung zu beachten.

Das Gleichgewicht der resultierenden Kräfte, die am Flächenelement (Bild 3.4) in Richtung
der X 1 –Koordinate angreifen, ist durch
�n 11 � �n 11��X 2 � �n 21 � �n 21��X 1 � p 1 �X 1 �X 2 � n 11 �X 2 � n 21 �X 1 � 0
– 3 / 6 –
(3.10.1)
gegeben. In Richtung der X 2 –Koordinate erhält man in gleicher Weise den Ausdruck
�n (3.10.2)
12 � �n12��X2 � �n22 � �n22��X1 � p 2 �X1�X2 � n12�X2 � n22�X1 � 0.
Das Momentengleichgewicht um die Scheibennormale wird in der Mitte des Flächenschnitts
(Bild 3.4) aufgestellt
�n 12 �X 2��X 1 � �n 21 �X 1��X 2 � 0.
(3.10.3)
Durch Division mit (∆X 1 ∆X 2 ) und durch Bildung der Grenzübergänge (∆X 1 ) → 0 und
(∆X 2 ) → 0 folgen aus Gl. (3.10.1) und Gl. (3.10.2) die partiellen Differentialgleichungen
zur Beschreibung des Gleichgewichts der Scheibenkräfte zu
und
�n11 �n21
�
�X1 �X2 � p1 � 0
�n12 �n22
�
�X1 �X2 � p2 � 0,
(3.11.1)
(3.11.2)
während das Momentengleichgewicht Gl. (3.10.3) nach Division mit (∆X 1 ∆X 2 ) unmit–
telbar die Symmetrie der Schubkräfte ausdrückt.
n 12 � n 21 .
Mit der Abkürzung
�( )
�X� � ( ),�
(3.11.3)
(3.12)
zur Kennzeichnung von partiellen Ableitungen kann man Gl. (3.11.1) und Gl. (3.11.2)
auch durch
und
n 11 ,1 � n21 ,2 � p1 � 0
n 12 ,1 � n22 ,2 � p2 � 0
(3.13.1)
(3.13.2)
ersetzen. Wird der erste Index der Scheibenkräfte, der Ortsindex, der in Gl. (3.13) als
Summationsindex – oben und unten gleich – auftritt, allgemein mit α und der zweite
Index, der Richtungsindex, allgemein mit β bezeichnet, kann man Gl. (3.13.1) und
Gl. (3.13.2) zu einer Gleichung zusammenfassen.
n �� ,� � p� � 0.
(3.14)

Die Struktur von Gl. (3.14) stimmt vollständig mit der Struktur der Gleichung
N��n � 0
überein, die für den Druck–Zug–Stab das Gleichgewicht in Richtung der Stabachse beschreibt.
Sie ist bereits aus der LV Statik I bekannt. Der Stab ist statisch bestimmt, weil
zur Berechnung der Stabkraft N genau eine Gleichgewichtsbedingung existiert. Dagegen
führt das Ausschreiben von Gl. (3.14) auf zwei Gleichungen, nämlich Gl. (3.13.1)
und Gl. (3.13.2), die wegen Gl. (3.11.3) drei unbekannte Kraftgrößen enthalten, für die
aber nur zwei Gleichgewichtsbedingungen existieren. Die Scheibe ist also grundsätzlich
1–fach innerlich statisch unbestimmt. Zur Integration von Gl. (3.14) ist es daher erforderlich,
zusätzlich den Verträglichkeitszustand zu betrachten, um die fehlende Gleichung
zur eindeutigen Berechnung der Scheibenkräfte n 11 , n 22 und n 12 = n 21 zu
erhalten.
3.4.2 Verträglichkeit
Die Verträglichkeit ist formal durch die Gleichung
� K �� � �M ��
– 3 / 7 –
(3.15)
definiert. Die Struktur von Gl. (3.15) stimmt mit der Struktur der äquivalenten Stabgleichung
� K � � M
überein, die den Dehnungszustand in Richtung der Stabachse erfaßt. Der Index (K)
kennzeichnet den kinematischen und der Index (M) den materiellen Verzerrungszustand.
Beide Anteile von Gl. (3.15) sind speziell für Scheibentragwerke abzuleiten.
3.4.2.1 Kinematischer Verzerrungszustand
Der kinematische Verzerrungszustand �K �� ist am verformten Flächenschnitt zu ermitteln,
der sich unter der Wirkung der Scheibenkräfte nαβ einstellt. Dabei ist die arbeitskonforme
Zuordnung dieser Größen zu beachten. Die Situation vor und nach der Verformung
ist im (Bild 3.5) dargestellt.
Im unverformten Zustand nimmt die Spannungsfläche A 1 die Position links (1,3) und
rechts (2,4) ein. Sie bewegt sich unter der Wirkung von n 11 und n 12 in die Position
(1,3)’ und (2,4)’. Für die Spannungsfläche A 2 gelten im unverformten Zustand die
Positionen unten (1,2) und oben (3,4). Sie gehen unter Wirkung von n 21 und n 22
in die verformten Positionen (1,2)’ und (3,4)’ über. Die Längszugkräfte n 11 und n 22
dehnen das Flächenelement, n 11 in Richtung der X 1 –Koordinate um � K 11 und n22 in
Richtung der X 2 –Koordinate um � K 22 . Die Schubkräfte n12 = n 21 bewirken dagegen

eine Schiefstellung bzw. Gleitung des Flächenelements um die Winkel � K 12 und �K 21 ,
vgl. (Bild 3.5). Zur Erreichung einer einheitlichen Bezeichnung ist es üblich, die Gleitungen
auch als Schubdehnungen bzw. noch einfacher als Dehnungen zu bezeichnen.
∆u 2
∆X 2
n 11
n 12
1 = 1’
X 2 ,A 2,u 2
∆u 1
n 21
∆X 1
Bild 3.5 : Verformter Flächenschnitt
3’
� K 12
n 22
n 22
∆s 1
– 3 / 8 –
� K 22
�K 21
n21 3 4
2
n 12
∆u 1
2’
n 11
4’
∆s 2
∆u 2
� K 11
X 1 ,A 1,u 1
Grundlage der Betrachtung ist die Theorie I. Ordnung. Die Kinematik ist daher konsequent
zu linearisieren. Im Rahmen dieser Annahme sind die Dehnungen durch
und
�K 11 � �u1 �X1��X 1 �
�0
�u1 �X1 � u1,1 �K 22 � �u2 �X2��X 2 �
�0
�u2 �X2 � u2,2 und die Gleitungen durch
�K 12 � �u2 �X1��X 1 �
�0
�u2 �X1 � u2,1 (3.16.1)
(3.16.2)
(3.16.3)

und
�K 21 � �u1 �X2��X 2 �
�0
�u1 �X2 � u1,2 definiert. Die Kurzform von Gl. (3.16) ist durch
� K �� � u �,�
– 3 / 9 –
(3.16.4)
(3.17)
gegeben. Die Vertauschung der Indizierung auf der rechten Seite von Gl. (3.17), die sich
unmittelbar durch Gl. (3.16.3) und Gl. (3.16.4) ergibt, ist bei der Auswertung zu beachten.
3.4.2.2 Materieller Verzerrungszustand
Das Materialverhalten ist in der Prüfungsmaschine zu erkunden. Läßt man z.B. im Versuch
Dehnungen auf ein Scheibenelement einwirken, kann man die daraus resultierenden
Kräfte messen. Natürlich kann man auch in umgekehrter Reihenfolge vorgehen
und Kräfte einprägen und die daraus resultierenden Dehnungen messen. Im Rahmen
der hier betrachteten Scheibentheorie soll uneingeschränkt elastisches und isotropes
Materialverhalten gelten. Es sind daher lediglich zwei Materialparameter zu bestimmen:
Der Elastizitätsmodul E und die Querdehnzahl ν.
Der Elastizitätsmodul, der die Steifigkeit des verwendeten Materials ausdrückt, ist bereits
von der Theorie der Stabtragwerke bekannt. Neu ist dagegen die Querdehnzahl.
Sie gibt die Größe der Querverkürzung an, die beim Zugversuch in flächigen Prüfkörpern
jeweils quer zur Richtung der Zugkraft auftritt. Wirken die Zugkräfte n 11 und n 22
auf ein Scheibenelement ein, erhält man die arbeitskonformen Dehnungen
und
� M 11
� M 22
� 1
Et �n 11 � �n 22�
� 1
Et �� �n 11 � n 22� .
(3.18.1)
(3.18.2)
Der Zusammenhang zwischen Kräften und Dehnungen ist im (Bild 3.6) dargestellt.
(Bild 3.6a) veranschaulicht die Wirkung von n 11 und (Bild 3.6b) die Wirkung von n 22 .
Zusätzlich ist im (Bild 3.6c) die Wirkung der Schubkräfte n 12 = n 21 dargestellt, die zur
Schiefstellung des Prüfkörpers führt. Diese Schiefstellung kann sich aber auch unter
der Wirkung der gleichwertigen Kräfte n Z und n D einstellen, die in Richtung der
Zug– und Druckdiagonalen angreifen. Für sie gilt Gl. (3.18) ebenfalls, wenn man
n 11 und n 22 durch n Z und n D ersetzt und die Abhängigkeiten n D = –n Z und
n Z = 1/2(n 12 + n 21 ) = n 12 = n 21 beachtet.

n 11
a) Wirkung von n 11
n 22
n 22
b) Wirkung von n 22
Bild 3.6 : Zusammenhang zwischen Kräften und Dehnungen
Die Zugdiagonale wird um das Maß
� M
Z
� 1 � �
Et n Z
n Z
n 12
n D
gedehnt und die Druckdiagonale um das Maß
� M
D � 1 � �
Et n D
– 3 / 10 –
n 11
n 21
n 21
c) Wirkung von n 12 = n 21
n D
n 12
n Z
(3.19.1)
(3.19.2)

gestaucht. Den Zug–Druck–Zustand der Schiefstellung Gl. (3.19) kann man natürlich
auch durch die Überlagerung der Einzelzustände
und
� M 12
� M 21
� 1 � �
Et n12
� 1 � �
Et n21
– 3 / 11 –
(3.20.1)
(3.20.2)
erzeugen, weil n Z und n D aus n 12 und n 21 gebildet werden. Die Überlagerung von
Gl. (3.20.1) und Gl. (3.20.2) ergibt dann
�� M 12 � �M 21 � �
2(1 � �)
n
Et
12 �
2(1 � �)
n
Et
21 .
(3.21)
Mit Gl. (3.18) und Gl. (3.20) ist das elastische Materialverhalten von Scheiben in eindeutiger
Weise festgelegt. Die Zusammenfassung in Form einer Matrizengleichung ergibt
� M 11
� M 22
� M 12 � �M 21
oder in Kurzform
mit
= D*
� M �� � D*E ���� n��
D*� 1
Et
1 –ν 0
–ν 1 0
0 0
2(1 + ν)
n 11
n 22
n 12 = n 21
,
(3.22.1)
(3.22.2)
(3.23)
als Scheiben– bzw. Dehnnachgiebigkeitsfaktor und Eαβρλ als Elastizitätsmatrix in
Nachgiebigkeitsform. Gl. (3.22) gilt bei Vorgabe des Kraftzustands und wird z.B. zur
Auswertung der Verträglichkeitsbedingung Gl. (3.15) benötigt. Vielfach ist es aber auch
erforderlich, den Wegzustand vorzugeben. Dies trifft immer dann zu, wenn es darum
geht, Kraftzustände durch Wegzustände auszudrücken. Die Invertierung von Gl. (3.22)
ergibt
n 11
n 22
n 12 = n 21
= D
1 ν 0
ν 1 0
0 0
1 � �
2
� M 11
� M 22
� M 12 � �M 21
,
(3.24.1)

oder in Kurzform
mit
n �� � DE ���� � M ��
D � Et
1 � � 2
– 3 / 12 –
(3.24.2)
(3.25)
als Scheiben– bzw. Dehnsteifigkeitsfaktor und E ���� als Elastizitätsmatrix in Steifigkeitsform.
3.4.2.3 Berechnungsgleichungen
In Gl. (3.15) ist die Kinematik Gl. (3.17) und das Materialgesetz Gl. (3.22.2) einzusetzen,
um die Kurzform der Berechnungsgleichungen der Verträglichkeit zu erhalten.
u �,� � D*E ���� n �� � 0.
Die Struktur von Gl. (3.26) stimmt vollständig mit der Struktur der Stabgleichung
u�� N
� 0
EA
(3.26)
überein. Die Auswertung von Gl. (3.26) unter Beachtung von Gl. (3.22.1) und Gl. (3.23)
ergibt drei unabhängige Berechnungsgleichungen, nämlich
und
u 1,1 � D*�n 11 � �n 22� � 0,
u 2,2 � D*�� �n 11 � n 22� � 0
�u 2,1 � u 1,2 � � 2(1 � �)D*�n 12 � n 21� � 0.
(3.27.1)
(3.27.2)
(3.27.3)
Sie beschreiben in Scheibentragwerken den verträglichen Zustand zwischen Kinematik
und Material. Die Kinematik hängt von den Eigenschaften des speziell betrachteten
Tragwerks ab. Haupteinflußparameter sind die Tragwerks– bzw. Bauteilgeometrie und
der Beanspruchungszustand. Die Verformbarkeit des Materials ist dagegen ausschließlich
eine Eigenschaft des eingesetzten Materials. Ziel eines jeden konstruktiven
Prozesses ist es, Kinematik und Material optimal aufeinander abzustimmen, um Bauschäden
zu vermeiden. Dies geschieht im Rahmen der Scheibentheorie mit Hilfe von
Gl. (3.27).

3.4.3 Bilanz
Die Bilanz im Gleichgewicht Gl. (3.13) bzw. Gl. (3.14) hat ergeben, daß zur Berechnung
der drei unbekannten Kraftgrößen n 11 , n 22 und n 12 = n 21 nur zwei unabhängige
Gleichungen existieren. Die Bilanz der Verträglichkeit Gl. (3.26) bzw. Gl. (3.27) ergibt
nun aber, daß zur Berechnung der zwei unbekannten Weggrößen u 1 und u 2 drei un–
abhängige Gleichungen existieren. Die Gesamtbilanz zwischen den fünf unbekannten
Größen (n 11 , n 22 , n 12 = n 21 , u 1, u 2) und den dazu zur Verfügung stehenden fünf unabhängigen
Berechnungsgleichungen (3.13) und (3.27) ist ausgeglichen. Das Scheibenproblem
ist daher eindeutig, wenn auch 1–fach statisch unbestimmt zu lösen. Bei der
Integration sind die aktuellen statischen und geometrischen Randbedingungen zu beachten.
3.4.4 Randbedingungen
Die Ränder von Scheiben der Baupraxis sind in der Regel geradlinig begrenzt. Vielfach
verlaufen die Ränder sogar parallel zu den X 1 – und X 2 –Koordinaten, z.B. bei Wandscheiben.
Die Formulierung der Randbedingungen kann sich daher auf den Fall schiefwinkliger,
aber gerader Ränder beschränken.
Ein Ausschnitt aus einem schiefen Scheibenrand R ist im (Bild 3.7) dargestellt. Die
Schiefe ist durch den Randwinkel ω gegeben. Tangential und radial bzw. normal zum
Rand sind die Einheitsvektoren
und
t 1
t = = =
t 2
r 1
t 1
t 2
r = = =
r 2
r 1
r 2
–sinω
cosω
cosω
sinω
– 3 / 13 –
(3.28.1)
(3.28.2)
definiert. Sie werden durch Komponenten in Richtung der X 1 – und X 2 –Koordinaten
aufgespannt. In Richtung dieser Vektoren zeigen die Randverschiebungen u r und u t
und die dazu arbeitskonformen Randkräfte n r und n t, die in der Randspannungs–
fläche A der Länge ∆s wirken. In diesen Weg– und Kraftgrößen, die sich aus den
Scheibenverschiebungen u 1 und u 2 und den Scheibenkräften n 11 , n 22 und n 12 = n 21
ableiten, sind die geometrischen und statischen Randbedingungen zu erfüllen.

u 2
X 2
∆X 2
n 11
n 12
Bild 3.7 : Schiefer Scheibenrand
s
A
A 1
ω
A 2
n 21
t
∆X 1
– 3 / 14 –
u t,n t
r
n 22
ω
∆s
u r,n r
ω
Scheiben–
rand R
Die Scheibenverschiebungen u 1 und u 2 zeigen in Richtung der X 1 – und X 2 –Koordi–
naten. Es ist lediglich eine Richtungsformation erforderlich, um die Randverschiebungen
u r und u t zu erhalten. Der Zusammenhang ist den Skizzen
cosω u 1
sinω u 2
zu entnehmen. Es gilt
und
ω
u r
ω
u 1
ur � cos� u 1 � sin� u 2 � r � u�
u 2
u t ��sin� u 1 � cos� u 2 � t � u� ,
u 2
ω
–u 1
u t
ω
X 1
cosω u 2
u 1
–sinω u 1
(3.29.1)
(3.29.2)
wobei sich die Kurzformen unmittelbar aus dem Vergleich mit Gl. (3.28) ergeben.

Die Scheibenkräfte n 11 , n 22 und n 12 = n 21 sind orts– und richtungsbezogen. Es ist
daher eine Doppeltransformation erforderlich, um die Randkräfte zu erhalten. Zu–
nächst ist die Ortstransformation durchzuführen, in dem man die resultierenden Randkräfte
n 1 und n 2 in Richtung der X 1 – und X 2 –Koordinaten bestimmt. Es gilt
und
n 1 �s � n 11 �X 2 � n 21 �X 1
n 2 �s � n 12 �X 2 � n 22 �X 1 .
Mit den Projektionen
und
�X 1 � sin��s
�X 2 � cos��s
der Randlänge ∆s erhält man
und
n 1 � cos�n 11 � sin�n 21
n 2 � cos�n 12 � sin�n 22
oder in Kurzform
n � � r�n �� ,
– 3 / 15 –
(3.30)
die wiederum aus dem Vergleich mit Gl. (3.28) folgt. Nach der Ortstransformation
Gl. (3.30) ist die Richtungstransformation von n β vorzunehmen. Sie ist genauso durchzuführen,
wie bei den Verschiebungen Gl. (3.29). Es gilt
und
nr � r � n � � r�r � n ��
n t � t � n � � r�t � n ��
oder ausgeschrieben
und
nr � cos 2 �n 11 � 2sin�cos�n 12 � sin 2 �n 22
n t ��sin�cos�n 11 � �cos 2 � � sin 2 ��n 12 � sin�cos�n 22 .
(3.31.1)
(3.31.2)
(3.31.3)
(3.31.4)

Weggrößen, hier die Verschiebungen Gl. (3.29) sind auf dem Teilrand R W vorzuschreiben
und Kraftgrößen, hier die Kräfte Gl. (3.31) auf dem Teilrand R K, wobei die Summe
der Teilränder den Gesamtrand R bildet. Für geometrische Randbedingungen auf R W
gilt die Vorgabe
u r
u t
=
u r
u t
und für statische Randbedingungen auf R K
n r
n t
=
n r
n t
.
– 3 / 16 –
(3.32.1)
(3.32.2)
Die Randbedingungen der Weg– und Kraftgrößen Gl. (3.32) können auch in gemischter
Form auftreten. Sind die vorgeschriebenen Werte u r und u t bzw. n r und n t auf Null
gesetzt, liegen homogene, ansonsten inhomogene Randbedingungen vor. Durch
Gl. (3.32) kann man über vier unabhängige Randgrößen verfügen. Das Integrationsproblem
der Scheibentheorie ist demnach von vierter Ordnung.
3.5 Lösungswege der Scheibentheorie
Es bieten sich drei Wege zur Lösung der Grundgleichungen der Scheibentheorie an,
die auf grundsätzlich unterschiedlichen Formulierungen beruhen.
3.5.1 Gemischte Formulierung in Weg– und Kraftgrößen
Bei dieser Vorgehensweise werden die Grundgleichungen (3.14) und (3.26) unter Beachtung
der Randbedingungen Gl. (3.32) direkt als Differentialgleichungssystem erster
Ordnung integriert. Analytisch ist dies kaum möglich, weil fünf Funktionen, nämlich
und
u 1 = u 1(X 1 ,X 2 ) ,
u 2 = u 2(X 1 ,X 2 ) ,
n 11 = n 11 (X 1 ,X 2 ) ,
n 22 = n 22 (X 1 ,X 2 )
n 12 = n 21 = n 12 (X 1 ,X 2 )
simultan zu integrieren sind, die jeweils von den Flächenkoordinaten X 1 und X 2 abhängen.
Numerische Lösungen sind dagegen bekannt. Sie beruhen in der Regel auf Differenzen–
oder Mehrstellenverfahren, die hier aber nicht weiter betrachtet werden.

3.5.2 Gleichgewichtsformulierung in Weggrößen
Bei dieser Vorgehensweise werden die Kraftgrößen vor der Integration eliminiert. Dazu
ist die Verträglichkeitsbedingung Gl. (3.26) nach den Kraftgrößen aufzulösen und in die
Gleichgewichtsbedingung Gl. (3.14) einzusetzen. Mit
n �� � DE ���� u �,�
– 3 / 17 –
(3.33)
und konstanten Materialwerten erhält man ein Differentialgleichungssystem, das aus
zwei Differentialgleichungen zweiter Ordnung besteht.
DE ���� u �,�� � p � � 0.
Das Ausschreiben von Gl. (3.33) ergibt die Bestimmungsgleichungen
und
n 11 � D�u 1,1 � �u 2,2 � ,
n 22 � D��u 1,1 � u 2,2 � ,
n 12 � n 21 � D
1 � ��u
2 1,2 � u � 2,1
(3.34)
(3.35.1)
(3.35.2)
(3.35.3)
der Scheibenkräfte und das Ausschreiben von Gl. (3.34) unter Beachtung von Gl. (3.35)
die partiellen Differentialgleichungen
und
D�2u 1,11 � (1 � �)u 1,22 � (1 � �)u 2,12 � � 2p 2 � 0
D�2u 2,22 � (1 � �)u 2,11 � (1 � �)u 1,12 � � 2p 2 � 0
(3.36.1)
(3.36.2)
zur Berechnung der Scheibenverschiebungen. Die analytische Integration von
Gl. (3.36) unter Beachtung der Randbedingungen Gl. (3.32) ist einfacher als bei der
gemischten Vorgehensweise, weil nur noch zwei Funktionen, nämlich
und
u 1 = u 1(X 1 ,X 2 )
u 2 = u 2(X 1 ,X 2 )
der simultanen Integration unterliegen. Bei technisch interessanten Anwendungen gelingt
es allerdings kaum, geschlossene Lösungen zu finden. Bei numerischen Lösungen
spielt die Formulierung in Weggrößen dagegen eine große Rolle. So beruhen z.B. fast
alle praxisrelevanten FE–Programme zur Lösung von Scheibenproblemen auf eine
schwache Formulierung der Gl. (3.34), die mit dem PvW übereinstimmt, vgl. Teil 7.

3.5.3 Verträglichkeitsformulierung in Kraftgrößen
Bei dieser Vorgehensweise werden vor der Integration die Weggrößen eliminiert. Vorab
ist daher eine geeignete Kraftgröße zu definieren, um dies zu erreichen. Dabei ist anzustreben,
die Anzahl der direkten Integrationsfunktionen deutlich zu reduzieren.
Bei der Verwendung von nur einer Variablen sind alle Funktionen
F � F�X 1 ,X 2�
– 3 / 18 –
(3.37)
zulässig, die als Nebenbedingung das homogene Gleichgewicht der Scheibenkräfte
n 11 , n 22 und n 12 = n 21 erfüllen. Dies leistet der Ansatz
und
n 11 � F ,22 ,
n 22 � F ,11
n 12 � n 21 ��F ,12 .
(3.38.1)
(3.38.2)
(3.38.3)
Setzt man Gl. (3.38) zur Kontrolle in Gl. (3.13) ein, erhält man unter der Voraussetzung
von p 1 ≡ 0 und p 2 ≡ 0 die Ausdrücke
und
n11 ,1 � n21 ,2 � F ,221 � F ,122 � 0
n12 ,1 � n22 ,2 ��F ,121 � F ,112 � 0.
Sie verschwinden identisch, wenn man die Vertauschbarkeit von partiellen Ableitungen
beachtet.
Alle Funktionen Gl. (3.37), die Gl. (3.38) erfüllen, werden als Spannungsfunktionen bezeichnet.
Aus baustatischer Sicht sind sie als mathematisch definierte statisch bestimmte
Grundsysteme der Scheibentheorie aufzufassen. Gl. (3.38) ist in die Verträglichkeitsbedingung
Gl. (3.26) bzw. Gl. (3.27) einzusetzen, um die Verschiebungen u 1
und u 2 aus den Grundgleichungen zu eliminieren. Dadurch erhält man die Gleichungen
und
u 1,1 � D*�F ,22 � �F ,11 � � 0, (3.39.1)
u 2,2 � D*�� �F ,22 � F ,11 � � 0 (3.39.2)
�u 1,2 � u 2,1 � � D*2(1 � �)F ,12 � 0. (3.39.3)

Das zweimalige partielle Ableiten von Gl. (3.39.1) nach der X 2 –Koordinate, von
Gl. (3.39.2) nach der X 1 –Koordinate und das gemischte partielle Ableiten von
Gl. (3.39.3) nach der X 1 – und X 2 –Koordinate ergibt
und
u 1,122 � D*�F ,2222 � �F ,1122 � � 0, (3.40.1)
u 2,211 � D*�� �F ,2211 � F ,1111 � � 0 (3.40.2)
�u 1,212 � u 2,112 � � D*2(1 � �)F ,1212 � 0. (3.40.3)
Addiert man nun Gl. (3.40.1) und Gl. (3.40.2) und subtrahiert die Summe von
Gl. (3.40.3), entfallen die Verschiebungen, wenn man die Vertauschbarkeit der partiellen
Ableitungen beachtet. Man erhält mit D* > 0 zunächst den Ausdruck
2(1 � �)F ,1212 � F ,1111 � F ,2222 � �F ,1122 � �F ,2211 � 0
und unter Beachtung der Vertauschbarkeit von partiellen Ableitungen die partielle Differentialgleichung
vierter Ordnung
F ,1111 � 2F ,1122 � F ,2222 � 0 (3.41)
mit der Spannungsfunktion F als einzig verbleibender Integrationsfunktion. Mit der
Definition des Operators
und
� � ( ) ,11 � ( ) ,22 (3.42.1)
�� � � 2 � ( ) ,1111 � 2( ) ,1122 � ( ) ,2222 (3.42.2)
kann man Gl. (3.41) auch in kurzer Form schreiben
��F � 0. (3.43)
Gl. (3.43) ist eine spezielle Formulierung der Verträglichkeit. Da die Spannungsfunk–
tion F implizit das Gleichgewicht erfüllt, erfaßt Gl. (3.43) das Scheibenproblem in vollständiger
Form. Sie wird daher auch als Scheibengleichung bezeichnet.
Die Integration von Gl. (3.43) ist unter Beachtung der Randbedingungen Gl. (3.32)
vorzunehmen. Ist für F eine Lösung ermittelt, sind durch Gl. (3.38) auch die Scheibenkräfte
n 11 , n 22 und n 12 = n 21 bekannt, in dem man die partiellen Ableitungen von F
bildet. Die Berechnung der Verschiebungen ist aufwendiger, weil dies eine Integration
erfordert. Es kann z.B. dadurch geschehen, daß man Gl. (3.39) integriert. Da die Verschiebungen
bei der Integration von Gl. (3.43) nicht explizit vorliegen, bereitet es vor
allem bei statisch unbestimmt gelagerten Scheiben erhebliche Schwierigkeiten, geometrische
Randbedingungen gemäß Gl. (3.32.1) zu berücksichtigen. Baupraktisch re-
– 3 / 19 –

levante Lösungen von Scheibenproblemen mit Gl. (3.43) sind daher nur im begrenzten
Umfang möglich.
3.6 Lösungsmethoden der Scheibentheorie
Das baustatische Verfahren von Schleeh, die Gitterrostmethode (GRM) und die
Methode der finiten Elemente (FEM) sind von Interesse, wenn es darum geht, baupraktische
Scheibenprobleme zu lösen. Die GRM wird im Teil 6 und die FEM im Teil 7
behandelt. Das Verfahren von Schleeh ist ausführlich in /6/ beschrieben. Eine kurze
Diskussion der Vorgehensweise soll die theoretischen Grundlagen des Verfahrens verdeutlichen.
Die praktische Anwendung anhand eines Zahlenbeispiels erfolgt im Abschnitt
3.7.
Das Verfahren von Schleeh setzt voraus, daß man den Beanspruchungszustand in
Scheiben in zwei Anteile aufspalten kann. Der erste Anteil ist ein Gleichgewichtszustand.
Er erstreckt sich in der Regel über das gesamte Scheibengebiet und ist in ein–
facher Weise mit Hilfe der technischen Biegetheorie ebener Balken zu ermitteln. Die
Gültigkeit dieser Lösung, die auf der Bernoulli–Hypothese vom Ebenbleiben der Querschnitte
beruht, ist an Längen–Höhen–Verhältnisse von L : H > 4 : 1 gebunden. Bei
realen Scheiben mit H ≈ L trifft diese Voraussetzung aber nicht mehr zu. Die Gleich–
gewichtslösung ist daher mit einem Eigenspannungszustand zu überlagern, der sich in
der Regel nur über spezielle Teilbereiche des Scheibensystems erstreckt. Er muß alle
Zwänge erfassen, die sich aus den konstruktiven Abweichungen ergeben, die zwischen
Balken und Scheiben bestehen. Der scheibenverträgliche Eigenspannungszustand ist
mit Hilfe der Scheibengleichung (3.43) zu ermitteln.
Die Aufspaltung der Lösung in einen Balken– und einen Scheibenanteil ist im (Bild 3.8)
am Beispiel einer Wandscheibe dargestellt. Am oberen Rand wirkt in der Mitte eine
Einzellast F, die am unteren Rand je zur Hälfte von den dort angeordneten Auflagern
aufgenommen wird (Bild 3.8a).
Die Lösung am Biegebalken ist im (Bild 3.8b) dargestellt. Bei diesem Anteil ist der
Gleichgewichtszustand zwischen äußeren Einwirkungen und inneren Schnittgrößen
erfüllt. Die Längsspannung σ, die sich aus dem Biegemoment M errechnet und die
mit der Scheibenkraft n11 0 � �⋅t übereinstimmt, ist wegen der Bernoulli–Hypothese geradlinig
über den Querschnitt verteilt. Der Verlauf der Schubspannung τ, die sich
aus der Querkraft Q errechnet und die mit der Scheibenkraft n12 0 � �⋅t übereinstimmt,
ist wegen der schubspannungsfreien oberen und unteren Balkenränder parabolisch
über den Querschnitt verteilt. Spannungen quer zur Balkenachse treten im Rahmen der
technischen Biegetheorie nicht auf. Der 0–Index der Scheibenkräfte soll darauf hinweisen,
daß eine Balkenlösung vorliegt.
– 3 / 20 –

H
2
H
2
a) Wandscheibe
F
2
�t � n 12
0 �X 1 �� L
2 �
+
n 22
ÇÇÇ
ÇÇÇ
ÇÇÇ
L
2
Bild 3.8 : Wandscheibe. Anteil Biegebalken und Scheibentheorie
n 12
n 11
b) Anteil Biegebalken: Gleichgewichtszustand
F � t�� MdX2 �n 12�X 1 �� L
2 �
–
–
+
F
2
� R
Q–Verlauf
+
M–Verlauf
F
2 � t�� R dX2
c) Anteil Scheibentheorie: Eigenspannungszustand
� M
FL
4
F
2
F
u 2
X 2
F
F
2
+
X 1
– 3 / 21 –
u 1
L
2
–
� R
F
2
F
2
Mittel–
fläche
�t � n11 0 �X1 � 0�
–
+
+
–
–
t
�n 11�X 1 � 0�
F
2 � t�� R dX2

Die Scheibenkräfte n11 0 und n12
0 stimmen nur dann mit der Lösung Gl. (3.43) überein,
wenn die betrachtete Scheibe die Voraussetzungen der Balkentheorie erfüllt. Bei Abmessungen
H ≈ L und vor allem in den Einleitungsbereichen der Kräfte ergeben sich
mehr oder weniger große Abweichungen von der Bernoulli–Hypothese vom Ebenbleiben
der Querschnitte, die eine Korrektur der Balkenlösung erfordern. Da die Balkenlösung
aber bereits einen Gleichgewichtszustand bildet, kann es sich nur um eine Korrektur
der Verträglichkeit handeln, die auf einem Eigenspannungszustand beruht. Die
Korrekturgrößen ∆n11 , ∆n22 und ∆n12 bewirken eine Umlagerung der Scheibenkräfte,
ohne das sich die resultierenden Integralwerte
und
�
H
�
H
� L
n 11 X 2 dX 2 � M
n 12 dX 2 � Q
n 22 X 1 dX 1 � 0
der überlagerten Scheibenkräfte
und
n 11 � n 11
0 � �n11 ,
n 22 � �n 22
n 12 � n 12
0
verändern.
� �n12
Die Korrekturlösung ist im (Bild 3.8c) dargestellt. Der Eigenspannungszustand in der
Mitte (Index M) und am linken und rechten Rand (Index R) ist durch die Differenz zwischen
den dort wirkenden Einzelkräften am wirklichen System (Bild 3.8a) und der parabolisch
verteilten Lasteinleitung am Biegebalken (Bild 3.8b) definiert. Die Berechnung
erfolgt nach der Scheibengleichung (3.43). Die Verläufe von der Korrekturspannung
∆n 11 in der Mitte und ∆n 12 am Rand sind im (Bild 3.8c) skizziert. Nach dem Prinzip von
de Saint–Venant ist die Korrekturlösung nur unmittelbar in Störungsbereichen von Interesse.
Außerhalb dieser Bereiche klingt sie sehr schnell ab, so daß hier in guter Näherung
die Balkenlösung gilt. Man kann die Korrekturlösung daher unabhängig vom aktuell
betrachteten Scheibensystem ermitteln. Für wichtige Anwendungsfälle ist dies z.B.
in /6/ geschehen. Die Ergebnisse sind in Form von Tabellen bereitgestellt. Das Verfahren
von Schleeh ist daher sehr gut zur Durchführung von Handrechnungen geeignet.
– 3 / 22 –

3.7 Beispiel zum Verfahren von Schleeh
Das Zahlenbeispiel ist aus /6/ entnommen. Es orientiert sich an der Systemskizze
(Bild 3.8a). Für einen Biegebalken mit den Abmessungen L / H = 6 und t = 1. m sind
die Scheibenkräfte n 11 , n 22 und n 12 zu ermitteln, um die Genauigkeit der Spannungsberechnung
nach der Balkentheorie zu überprüfen. Die Störungsbereiche nach
de Saint–Venant , in denen die Abweichungen auftreten, sind im (Bild 3.9) dargestellt.
Die Länge der Störungsbereiche erstreckt sich jeweils über das Höhenmaß H der
Scheibe. Zur Verteilung der Einzellasten wird eine Lastbreite 0.1H angenommen. Die
Berechnung erfolgt am kinematischen Gleichgewichtssystem (Bild 3.9). Mit dieser
Maßnahme kann man das schwierige Problem der Erfüllung von geometrischen Randbedingungen
umgehen, die beim wirklichen System vorliegen, vgl. (Bild 3.8a). In der
Mitte des Balkens sind im Schnitt (X 1 = 0, X 2 ) die Scheibenkräfte n 11 und n 22 und
im Schnitt (X 1 = 0.05H, X 2 ) die Scheibenkraft n 12 zu berechnen.
Die Ergebnisse sind in (Tabelle 3.1) zusammengestellt. Die Zahlenwerte gelten für die
Einheitslast F = 1 kN und die Balkenhöhe H = 0.10 m. Angegeben sind die Gleichgewichtslösungen
nach der Balkentheorie, die Korrekturlösung nach der Scheibentheorie
und die gesuchte Gesamtlösung als Überlagerung der beiden Einzellösungen.
F
0.05H 0.05H
H H
0.05H 0.05H 0.05H 0.05H
F
2
H
L / 2 = 3H
Bild 3.9 : Gestörte Spannungsbereiche beim Biegebalken
X 2
L = 6H
X 1
– 3 / 23 –
L / 2 = 3H
H
F
2
H
2
H
2
H

X 2
H
0.5
0.4
0.3
0.2
0.1
0.0
–0.1
–0.2
–0.3
–0.4
–0.5
Gleichgewichtslösung nach
der Balkentheorie
n 11
0
–89.25
–71.40
–53.55
–35.70
–17.85
0.0
17.85
35.70
53.55
71.40
89.25
n 22
0
0.0
0.0
Tabelle 3.1 : Scheibenkräfte in (kN/m)
Korrekturlösung nach
der Scheibentheorie
– 3 / 24 –
Gesamtlösung durch Über–
lagerung der Einzellösungen
n 12
0 �n 11 �n 22 �n 12 n 11 n 22 n 12
0.0
2.7
4.8
6.3
7.2
7.5
7.2
6.3
4.8
2.7
0.0
–88.32
6.76
8.51
6.91
4.75
2.44
0.23
–1.62
–2.85
–3.12
–1.92
–100.00
–54.80
–29.81
–19.28
–13.25
–9.12
–6.00
–3.58
–1.73
–0.48
0.0
0.0
13.41
1.91
–2.68
–4.83
–5.76
–5.84
–5.24
–4.02
–2.25
0.0
–177.6
–64.6
–45.0
–28.8
–13.1
2.4
18.1
34.1
50.7
68.3
87.3
–100.0
–54.8
–29.8
–19.3
–13.3
–9.1
–6.0
–3.6
–1.7
–0.5
0.0
0.0
16.1
6.7
3.6
2.4
1.7
1.4
1.1
0.8
0.5
0.0
Bei der elementaren Berechnung der Gleichgewichtslösung ist die linienförmige
Lasteinleitung zu berücksichtigen und das Vorzeichen von Q an die Richtung von n12 0
anzupassen. Die Korrekturlösung kann für X1 = 0 und X1 / H = 0.05 unmittelbar aus
Tafel I auf Seite 786 von /6/ abgelesen werden. Die Verläufe der Scheibenkräfte sind
im (Bild 3.10) dargestellt.
Die Abweichungen, die sich zwischen Balken– und Scheibenlösung einstellen, sind
wegen L / H = 6 > 4 gering (Bild 3.10a). Nur im Wirkungsbereich der Einzellast erge–
ben sich größere Differenzen. Sie resultieren unmittelbar aus der Lasteinleitung und
sind im Regelfall ohne Bedeutung.
So erfolgt die Einleitung der mittigen Einzellast bei der Scheibe wirklichkeitsnah durch
die Scheibenkraft n 22 (Bild 3.10b). Im Rahmen der Balkentheorie tritt diese Größe nicht
auf. Die Einleitung beim Balken ist daher nur durch parabolisch verteilte Schubspannungen
möglich, was zwangsläufig zu einer Verletzung des lokalen Gleichgewichts
führt (Bild 3.10c).

177.6
89.3
ÇÇÇ
ÇÇÇ
ÇÇÇ
–
n 11
X 2
+
87.3
89.3
X 1 = 0
100.
Bild 3.10 : Verläufe der Scheibenkräfte, vgl. (Tabelle 3.1)
–
n 22
ÇÇÇ
ÇÇÇ
ÇÇÇ
– 3 / 25 –
X 2 X 2
X 1 = 0
n 21 = n 12
a) b) c)
ÇÇÇ
ÇÇÇ
ÇÇÇ
n 12
+
X 1 = 0.05H
7.5
61.
Scheibenlösung
Balkenlösung

Teil 4: Plattentheorie
4.1 Einführung
Die Plattentheorie beschreibt das baustatische Verhalten von ebenen Flächentragwerken,
bei denen die Lastebene eine Senkrechte zur Mittelfläche des dünnwandigen
Tragwerks bildet. Ziel ist es, zweidimensionale Weg– und Kraftgrößen zu definieren und
zu berechnen, die sich aus den allgemeinen dreidimensionalen Kontinuumsgrößen ergeben,
wenn man die geometrischen und physikalischen Voraussetzungen beachtet,
die Plattentragwerke charakterisieren. Diese Größen erfassen den Beanspruchungszustand
mit ausreichender Genauigkeit, um Plattentragwerke sicher und wirtschaftlich
planen und bemessen zu können, vgl. z.B. Einführungsbeispiel 1.5.2: Flach– und Pilzdecke.
Im Rahmen der Plattentheorie sind die Problemstellung zu formulieren, die
Grundgleichungen: Gleichgewicht und Verträglichkeit abzuleiten, allgemeine Lösungswege
aufzuzeigen und spezielle Lösungsmethoden zu entwickeln. Dies geschieht in
den Abschnitten 4.2 bis 4.6. Ein Beispiel im Abschnitt 4.7, das mit dem Verfahren von
Ritz berechnet wird, beschließt die Ausführungen zur Plattentheorie.
4.2 Voraussetzungen der Plattentheorie
Ein rechteckig begrenzter Ausschnitt aus einem dreidimensionalen Plattenkontinuum
ist im (Bild 4.1) dargestellt.
L 2 = B
X 3
f 3 ,v 3
X 2
f 2 ,v 2
Bild 4.1 : Plattenkontinuum
A 2
A 2
σ 3j ,ε 3j
m 22 ,β 22
q 23 ,γ 23
σ 2j ,ε 2j
A 3
L 1 = L
A 1
– 4 / 1 –
σ 1j ,ε 1j
Mittelfläche
m 21 ,β 21
p 3 ,u 3
Kontinuums–
größen
A 3
ϕ1 ϕ2 q 13 ,γ 13
Plattengrößen
m 11 ,β 11
m 12 ,β 12
L 3 = t
A 1
X 1
f 1 ,v 1

Die geometrische Beschreibung und die Restriktion der Abmessungen stimmen mit
den Gegebenheiten beim Scheibenkontinuum überein. Die Länge (L 1 = L) und die
Breite (L 2 = B) muß deutlich größer sein als die Dicke (L 3 = t). Es gilt
(L, B) �� t. (4.1)
Für Einwirkungen ist zu beachten, daß sie nur senkrecht zur Mittelfläche angreifen dürfen.
Für volumenbezogene Lasten gilt z.B. die Restriktion
f � � 0, (4.2)
so daß als Einwirkung die Flächenlast
p 3 �� t
f 3 dX 3
– 4 / 2 –
(4.3)
verbleibt. Gl. (4.3) ist z.B. in der Dimension (kN/m 2 ) anzugeben. Flächenlasten können
als Voll– oder Teillasten wirken. In der Lastebene senkrecht zur Mittelfläche können natürlich
auch Einzellasten und Einzelmomente, Linienlasten und Linienmomente oder
eingeprägte Weggrößen angreifen.
Der Beanspruchungszustand des statischen Modells Platte ist ein reiner Biegezustand.
Er ist durch drei Eigenschaften definiert:
1. Die Spannungsflächen A 3 , die das Plattenkontinuum (Bild 4.1) in Richtung der
X 3 –Koordinate nach außen begrenzen, sind als spannungsfrei anzunehmen.
2. In Richtung der Dicke soll sich der Plattenquerschnitt dehnstarr verhalten.
3. Es gilt die Bernoulli–Hypothese vom Ebenbleiben der Querschnitte.
Für Platten aus dem Bereich des konstruktiven Ingenieurbaus sind diese Annahmen in
guter Näherung erfüllt. Damit entfällt die X 3 –Koordinate als unabhängige Beschreibungskoordinate
und die Berechnung kann mit den im (Bild 4.1) dargestellten Plattengrößen
der Mittelfläche erfolgen.
4.3 Berechnungsgrößen der Plattentheorie
Durch die Hypothese vom Ebenbleiben der Querschnitte wird festgelegt, daß sich die
Verschiebungen v 1 und v 2 linear im Querschnitt verteilen.
0
v � �X � ,X 3� � u � (X � ) � X 3 ϕ � (X � ) . (4.4)

In Gl. (4.4) sind u 1 und u 2 Verschiebungen in der Plattenmittelfläche, die wegen der
Restriktion Gl. (4.2) nicht auftreten. ϕ 1 und ϕ 2 sind Verdrehungen der Plattenmittel–
fläche, die im Rahmen der Plattentheorie die Verschiebungen des Plattenkontinuums
v 1 und v 2 gleichwertig ersetzen.
In Anlehnung an Gl. (3.17), Teil 3: Scheibentheorie gilt: ε 33 = v 3,3 . Wegen der Annahme
der Dehnstarrheit in Dickenrichtung ε 33 ≡ 0 folgt unmittelbar v 3,3 = 0, so daß sich alle
Punkte im Querschnitt des Plattenkontinuums um das gleiche Maß durchbiegen. Die
Verschiebung v 3 stimmt daher mit der Durchbiegung u 3 der Plattenmittelfläche überein.
v 3 �X � ,X 3� � u 3 (X � ) . (4.5)
Die Spannungen σ αβ = σ βα , die in den Spannungsflächen Aα, α = 1, 2 im Abstand
X 3 parallel zur Mittelfläche in Richtung der X 1 – und X 2 –Koordinaten wirken, sind wegen
der Annahme vom Ebenbleiben der Querschnitte Gl. (4.4) linear im Querschnitt verteilt.
Weil in diesen Richtungen keine Einwirkung auftritt – es gilt Gl. (4.2) – , bilden sie innerhalb
der Querschnitte Gleichgewichtszustände, so daß man als resultierende Größen
der Mittelfläche Momente erhält.
m �� �� t
� �� X 3 dX 3 � m �� . (4.6)
Die Momente Gl. (4.6) sind längenbezogen. m 11 und m 12 beziehen sich auf die Länge
der X 2 –Koordinate und m 21 und m 22 auf die Länge der X 1 –Koordinate, vgl. (Bild 4.1).
Die Dimensionsangabe kann z.B. in (kNm/m) erfolgen.
Die Gleichgewichtsspannung σ 13 , die in der Spannungsfläche A 1 wirkt und die Gleichgewichtsspannung
σ 23 , die in der Spannungsfläche A 2 wirkt, zeigen in Richtung der
Flächenlast Gl. (4.3). Sie sind über die Dicke zu resultierenden Querkräften zusammenzufassen.
q �3 �� t
� �3 dX 3 . (4.7)
Die Querkräfte Gl. (4.7) sind längenbezogen. q 13 bezieht sich auf die Länge der
X 2 –Koordinate und q 23 auf die Länge der X 1 –Koordinate, vgl. (Bild 4.1). Die Dimensionsangabe
kann z.B. in (kN/m) erfolgen.
Den Schnittgrößen Gl. (4.6) und Gl. (4.7) sind arbeitskonform innere Weggrößen zugeordnet,
die sich ebenfalls auf die Mittelfläche beziehen. Im Fall der Momente Gl. (4.6)
sind es die Krümmungen
� �� � � �� (X � ) (4.8)
und im Fall der Querkräfte Gl. (4.7) die Gleitungen
� �3 � � �3 (X � ) . (4.9)
– 4 / 3 –

Mit Gl. (4.3) bis Gl. (4.9) sind alle Einwirkungs– und Berechnungsgrößen der Platten–
theorie definiert. Die arbeitskonforme Zuordnung ist im (Bild 4.2) dargestellt, vgl. auch
(Bild 4.1).
t
t
2
t
2
p 3 ,u 3
X 3
X 2
Mittelfläche
– 4 / 4 –
m21 q
,β21 23 ,γ23 ϕ 2,m 22 ,β 22
ϕ 1,m 11 ,β 11
m 12 ,β 12
q 13 ,γ 13
Bild 4.2 : Einwirkungs– und Berechnungsgrößen der Plattentheorie
Bei Vorgabe der Einwirkung p 3 sind zu berechnen:
– Zum Nachweis der Tragfähigkeit die Momente m αβ = m βα und ggf. die Quer–
kräfte q α3 .
– Zum Nachweis der Gebrauchstauglichkeit die Durchbiegung u 3 und ggf. die Verdrehungen
ϕα.
Dazu sind die Grundgleichungen für das Gleichgewicht und die Verträglichkeit aufzustellen
und analytisch oder numerisch zu lösen.
4.4 Grundgleichungen der Plattentheorie
4.4.1 Gleichgewicht
Im Rahmen der Theorie I. Ordnung ist der Gleichgewichtszustand von Platten am unverformten
System zu formulieren. Der Flächenschnitt mit den Gleichgewichtsgrößen
ist im (Bild 4.3) dargestellt. Bei der Formulierung des Kräfte– und Momentengleichgewichts
ist der Mittelwertsatz der Integralrechnung zu beachten.
X 1

m 12 ∆X 2
m 11 ∆X 2
q 13 ∆X 2
m 21 ∆X 1
∆X 2
∆X 1
X 2 ,A 2
q 23 ∆X 1
m 22 ∆X 1
Bild 4.3 : Flächenschnitt Plattentragwerk
– 4 / 5 –
p 3
(q 23 +∆q 23 )∆X 1
(m 21 +∆m 21 )∆X 1
(m 22 +∆m 22 )∆X 1
(m 11 +∆m 11 )∆X 2
(m 12 +∆m 12 )∆X 2
(q 13 +∆q 13 )∆X 2
X 1 ,A 1
Das Kräftegleichgewicht in Richtung der Flächenlast p 3 ist durch die Kräftesumme
�q 13 � �q 13��X 2 � �q 23 � �q 23��X 1 � q 13 �X 2 � q 23 �X 1 � p 3 �X 1 �X 2 � 0 (4.10.1)
erfüllt. Das Momentengleichgewicht in der Mitte des Flächenschnitts ist für die X 1 – und
X 2 –Richtung aufzustellen. Für die X 1 –Richtung gilt die Momentensumme
�m 11 � �m 11��X 2 � �m 21 � �m 21��X 1 � m 11 �X 2 � m 21 �X 1 � q 13 �X 1 �X 2 � 0 (4.10.2)
und für die X 2 –Richtung die Momentensumme
�m 22 � �m 22��X 1 � �m 12 � �m 12��X 2 � m 22 �X 1 � m 12 �X 2 � q 23 �X 1 �X 2 � 0. (4.10.3)
Wegen der Orthogonalität der X 1 – und X 2 –Koordinaten dreht die Momentensumme
der X 1 –Richtung Gl. (4.10.2) um die positive X 2 –Achse und die Momentensumme der
X 2 –Richtung Gl. (4.10.3) um die negative X 1 –Achse.

Durch Division mit (∆X 1 ∆X 2 ) und durch Bildung der Grenzübergänge (∆X 1 → 0) und
(∆X 2 → 0) folgen aus Gl. (4.10) die Differentialgleichungen
und
q 13 ,1 � q23 ,2 � p3 � 0, (4.11.1)
m 11 ,1 � m21 ,2 � q13 � 0 (4.11.2)
m 12 ,1 � m22 ,2 � q23 � 0. (4.11.3)
Die Kurzform von Gl. (4.11) ist unter Beachtung der Summationsregel durch
und
q �3 ,� � p 3 � 0 (4.12.1)
m �� ,� � q�3 � 0 (4.12.2)
gegeben. Die Struktur von Gl. (4.12) stimmt vollständig mit der Struktur der Gleichungen
und
Q��p � 0
M��Q � 0
überein, die für den Biegebalken gelten. Beim Balken ist die Bilanz zwischen den Unbekannten
und der Anzahl der Gleichungen ausgeglichen. Bei der Platte fehlen dagegen
zwei Gleichungen, um alle fünf Schnittgrößen, nämlich m 11 , m 22 , m 12 = m 21 , q 13 und
q 23 berechnen zu können. Platten sind also grundsätzlich 2–fach innerlich statisch unbestimmt.
Die fehlenden Gleichungen sind daher aus dem Verträglichkeitszustand zu
entwickeln.
4.4.2 Verträglichkeit
Die Verträglichkeit ist formal durch die Gleichungen
und
� K �� � �M ��
� K �3 � �M �3
– 4 / 6 –
(4.13.1)
(4.13.2)
definiert. Die Struktur von Gl. (4.13) stimmt vollständig mit der Struktur der äquivalenten
Balkengleichungen
� K � � M

und
� K � � M
überein, die den Krümmungs– und Gleitungszustand von Biegebalken erfassen. Der
Index (K) kennzeichnet den kinematischen und der Index (M) den materiellen Verzerrungszustand.
Beide Anteile von Gl. (4.13.1) und Gl. (4.13.2) sind speziell für Plattentragwerke
abzuleiten.
4.4.2.1 Kinematischer Verzerrungszustand
Der Verformungszustand von Platten ist im (Bild 4.4) dargestellt.
u 3
P Q
P M
Mittelfläche
verformter
Plattenquerschnitt
Normale
X 3
uα
Mittelfläche
vα
unverformter
Plattenquerschnitt
X 3
Bild 4.4 : Verformungszustand von Platten
X α
– 4 / 7 –
–u 3,α
P’ M
X 3 ϕα
ϕα
P’ Q
� K �3
–u 3,α
Normale
Hypothese
vom Eben–
bleiben der
Querschnitte
v 3 = u 3
Die mathematische Formulierung der Verschiebungen im Plattenkontinuum ist durch
Gl. (4.4) und Gl. (4.5) gegeben. Bezugsfläche ist die Mittelfläche des Kontinuums.
Punkte P M auf der unverformten Mittelfläche nehmen auf der verformten Mittelfläche
die Lage P’ M ein. Die tangentiellen Verschiebungen uα, α = 1, 2 zwischen den Punkten
P M und P’ M entfallen im Rahmen der Plattentheorie. Zwischen P M und P’ M ist allein
die Durchbiegung u 3 in Richtung der Normalen zu berücksichtigen. Sie erfaßt wegen
der Annahme der Dehnstarrheit in Dickenrichtung auch den Abstand zwischen den
Querschnittspunkten P Q und P’ Q, vgl. Gl. (4.5). Der verformungsbedingte tangentiale

Abstand zwischen den Punkten im Querschnitt P’ Q und Punkten auf der Mittelfläche
P’ M läßt sich wegen der Hypothese vom Ebenbleiben der Querschnitte ebenfalls durch
Größen der Mittelfläche, nämlich durch die Verdrehungen ϕα, α = 1, 2 ausdrücken, vgl.
Gl. (4.4).
Der kinematische Dehnungszustand von Flächen (Scheiben) im dickenstarren Plattenkontinuum,
die im Abstand X 3 parallel zur Mittelfläche liegen, ist in Anlehnung an
Gl. (3.17), Teil 3: Scheibentheorie durch
und
� K �� � v �,�
� K �3 � v 3,�
� K 3� � v �,3
, (4.14.1)
gegeben. Gl. (4.4) und Gl. (4.5) in Gl. (4.14) eingesetzt, ergibt
und
– 4 / 8 –
(4.14.2)
(4.14.3)
� K �� � X3 ϕ �,� , (4.15.1)
� K �3 � u 3,�
(4.15.2)
� K 3� � ϕ� . (4.15.3)
Die Dehnungsausdrücke in Gl. (4.15) hängen zwar von Größen der Plattenmittelfläche
ab, stellen aber immer noch Dehnungen des Plattenkontinuums dar. Sie sind daher
durch Integration auf die Plattenmittelfläche zu reduzieren. Dies hat im Zusammenhang
mit den arbeitskonformen Spannungsgrößen σ αβ , σ α3 und σ 3α = σ α3 zu geschehen,
um die statische Gleichwertigkeit zwischen dem dreidimensionalen Plattenkontinuum
und der zweidimensionalen Plattentheorie zu gewährleisten. Unter Beachtung von
Gl. (4.6), Gl. (4.7) und Gl. (4.15) erhält man die Arbeitsausdrücke
� t
� �� � K �� dX3 �� t
und
� �
t
�3��K �3 � �K 3��dX3 ��
t
In Gl. (4.16.1) ist
� K �� � ϕ �,�
die Krümmung und in Gl. (4.16.2)
� �� X 3 dX 3 ϕ �,� � m �� ϕ �,� � m �� � K ��
(4.16.1)
��3dX3�u3,� � ϕ�� � q�3�u3,� � ϕ�� � q�3�K �3 . (4.16.2)
(4.17.1)

� K �3 � u 3,�
� ϕ�
(4.17.2)
– 4 / 9 –
die Gleitung der Plattenmittelfläche, die sich arbeitskonform zu den durch Gl. (4.6) und
Gl. (4.7) definierten Momenten und Querkräften der Plattenmittelfläche verhalten.
Die Gleitung Gl. (4.17.2) erfaßt im verformten Plattenquerschnitt die Abweichung von
der Normalen, vgl. (Bild 4.4). Plattentragwerke im konstruktiven Ingenieurbau sind wegen
Gl. (4.1) dünn. Der Einfluß der Gleitung auf das Tragverhalten ist von untergeord-
neter Bedeutung und wird daher im Rahmen einer schubstarren Plattentheorie vernachlässigt.
Mit �K �3 � 0 folgt aus Gl. (4.17.2) die Normalenregel
ϕ� ��u 3,� . (4.18)
Gl. (4.18) drückt aus, daß die Normale nach der Verformung Normale bleibt, vgl.
(Bild 4.4). Gl. (4.18) in Gl. (4.17.1) eingesetzt, ergibt für die Krümmung den Ausdruck
� K �� ��u 3,��
. (4.19)
Durch Gl. (4.19) ist der kinematische Krümmungszustand von schubstarren Platten als
zweite partielle Ableitung der Durchbiegung u 3 nach den Koordinaten X 1 und X 2
definiert. Die arbeitskonforme Zuordnung zu den Momenten ist im (Bild 4.5) dargestellt.
Die Biegemomente m 11 im (Bild 4.5a) und m 22 im (Bild 4.5b) erzeugen jeweils eine
Zylinderbiegung und die Wirkung der Torsionsmomente m 12 = m 21 im (Bild 4.5c) führt
zu einer Verwindung der Plattenmittelfläche.
4.4.2.2 Materieller Verzerrungszustand
Der materielle Dehnungszustand von Flächen im Plattenkontinuum, die im Abstand X 3
parallel zur Mittelfläche liegen, ist durch
�M �
1
�� E E������� (4.20)
gegeben. Die Elastizitätsmatrix in der Nachgiebigkeitsform Eαβρλ ist durch Gl. (3.22.1),
Teil 3: Scheibentheorie bekannt. E ist der Elastizitätsmodul. In Analogie zu Gl. (4.15.1)
und Gl. (4.17.1) kann die materielle Dehnung Gl. (4.20) auch durch die materielle Krümmung
der Plattenmittelfläche ausgedrückt werden.
�M �� � X3�M �� . (4.21)

a) � K 11 ��u 3,11
u 3
b)
u 3
X 2
X 2
� K 22 ��u 3,22
m 22
X 1
X 1
m 11
c)
– 4 / 10 –
X 2
X 1
� 12 � � 21 ���u 3,12 � u 3,21 � ��2u 3,12
Bild 4.5 : Kinematischer Krümmungszustand von schubstarren Platten
Gl. (4.21) in Gl. (4.20) eingesetzt und nach den Spannungen aufgelöst, ergibt
u 3
m 21 = m 12
��� 3 � X
E
1 � �2 E�����M . �� (4.22)
m 12

Die Elastizitätsmatrix in der Steifigkeitsform E αβρλ ist durch Gl. (3.24.1), Teil 3: Scheibentheorie
bekannt. E ist der Elastizitätsmodul und ν die Querdehnzahl. Setzt man
nun Gl. (4.22) in die Definitionsgleichung der Momente Gl. (4.6) ein, so erhält man unter
Beachtung der Integration
�t�2
�
�t�2
�X
3� 2
dX3 � t3
12
den Zusammenhang zwischen den Plattenmomenten und der materiellen Krümmung
Der Faktor
m �� � BE ���� � M ��
B �
Et3
12�1 � � 2�
. (4.23.1)
– 4 / 11 –
(4.24)
definiert die Steifigkeit von Platten und wird daher auch als Plattensteifigkeit bezeichnet.
Das Ausschreiben von Gl. (4.23.1) in Form einer Matrizengleichung ergibt
m 11
m 22
m 12 � m 21
� B
1 ν 0
ν 1 0
0 0
1 � �
2
� M 11
� M 22
� M 12 � �M 21
.
(4.23.2)
Durch die Invertierung von Gl. (4.23.2) erhält man den Zusammenhang zwischen den
materiellen Krümmungen und den Momenten ebenfalls in Form einer Matrizengleichung
� M 11
� M 22
� M 12 � �M 21
oder in Kurzform
� B*
1 −ν 0
−ν 1 0
0 0 2(1 � �)
m 11
m 22
m 12 � m 21
,
(4.25.1)
� M �� � B*E ���� m�� . (4.25.2)

Der Faktor
B*� 12
Et 3
– 4 / 12 –
(4.26)
definiert die Nachgiebigkeit von Platten und wird daher auch als Plattennachgiebigkeit
bezeichnet.
Mit �K �3 � 0 ist wegen Gl. (4.13.2) auch �M �3 � 0. Damit entfällt im Fall von schubstarren
Platten das Materialgesetz, das den elastischen Zusammenhang zwischen den
Querkräften und den materiellen Gleitungen definiert. Es ist eine Gleichgewichtsbedingung
erforderlich, um die Querkräfte zu berechnen. Sie ist durch die Momentengleichgewichtsbedingung
Gl. (4.12.2) bekannt, die im Fall von schubstarren Platten als Definitionsgleichung
zur Berechnung der Querkräfte
q �3 � m �� ,�
(4.27)
dient. Setzt man nun Gl. (4.27) in die Kräftegleichgewichtsbedingung Gl. (4.12.1) ein,
so nimmt das Kräftegleichgewicht von schubstarren Platten die Kurzform
m �� ,�� � p3 � 0. (4.28)
an. Gl. (4.28) stellt eine partielle Differentialgleichung zweiter Ordnung dar. Das Ausschreiben
m 11 ,11 � 2m12 ,12 � m22 ,22 � p3 � 0 (4.29)
zeigt, daß für das Gleichgewicht eine Berechnungsgleichung mit drei unbekannten
Kraftzuständen, nämlich den Momenten m 11 , m 22 und m 12 = m 21 vorliegt.
4.4.2.3 Berechnungsgleichungen
In Gl. (4.13.1) ist die Kinematik Gl. (4.19) und das Materialgesetz Gl. (4.25.2) einzusetzen,
um die Kurzform der Berechnungsgleichung der Verträglichkeit zu erhalten.
u 3,�� � B*E ���� m �� � 0. (4.30)
Gl. (4.30) stellt eine partielle Differentialgleichung zweiter Ordnung dar. Die Struktur
stimmt vollständig mit der Struktur der Balkengleichung
w�� � M
� 0
EI
überein. Das Ausschreiben von Gl. (4.30) unter Beachtung von Gl. (4.25.1) und
Gl. (4.26) ergibt drei unabhängige Berechnungsgleichungen, nämlich

und
u 3,11 � B*�m 11 � �m 22� � 0, (4.31.1)
u 3,22 � B*�� �m 11 � m 22� � 0 (4.31.2)
u 3,12 � B*(1 � �)�m 12 � m 21� � 0. (4.31.3)
Unbekannter Wegzustand ist die Durchbiegungsfunktion u 3 = u 3(X 1 , X 2 ). Im Rahmen
des konstruktiven Prozesses sind Kinematik und Material optimal aufeinander abzustimmen.
Dies geschieht bei Plattentragwerken mit Hilfe von Gl. (4.31).
4.4.3 Bilanz
Im Gleichgewicht Gl. (4.28) bzw. Gl. (4.29) hat die Bilanz zwischen Anzahl der Unbekannten
und Anzahl der verfügbaren Gleichungen ergeben, daß zur Berechnung der
Momente m 11 , m 22 und m 12 = m 21 nur eine unabhängige Gleichung existiert. Die
Bilanz der Verträglichkeit Gl. (4.30) bzw. Gl. (4.31) ergibt nun aber, daß zur Berechnung
der Durchbiegung u 3 drei unabhängige Gleichungen existieren. Die Gesamtbilanz
zwischen den vier unbekannten Größen (m 11 , m 22 , m 12 = m 21 , u 3) und den dazu zur
Verfügung stehenden vier unabhängigen Berechnungsgleichungen ist demnach ausgeglichen.
Das Plattenproblem ist also eindeutig, wenn auch 2–fach statisch unbestimmt
zu lösen. Bei der Integration sind die aktuellen statischen und geometrischen
Randbedingungen zu beachten. Mit den Momenten und der Durchbiegung sind bei
schubstarren Platten auch die Querkräfte und die Verdrehungen bekannt. Die Querkräfte
folgen wegen Gl. (4.27) aus der partiellen Ableitung der Momente und die Verdrehungen
wegen Gl. (4.18) aus der partiellen Ableitung der Durchbiegung.
4.4.4 Randbedingungen
Die Grundgleichungen von schubstarren Platten: Gleichgewicht Gl. (4.28) bzw.
Gl. (4.29) und Verträglichkeit Gl. (4.30) bzw. (4.31) sind jeweils partielle Differentialgleichungen
von 2–ter Ordnung, so daß insgesamt ein Integrationsproblem von 4–ter Ordnung
vorliegt. Es sind daher vier Randbedingungen zu formulieren, um eine eindeutige
Lösung zu erhalten. Die Vorgabe kann aus statischen, geometrischen oder aus einer
Kombination aus statischen und geometrischen Randbedingungen bestehen.
Die Weg– und Kraftzustände am schiefen Plattenrand sind im (Bild 4.6) dargestellt. Die
Randvektoren r und t sind wie beim schiefen Scheibenrand zu ermitteln, vgl. (Bild 3.7),
Teil 3: Scheibentheorie. Die Randverdrehungen, die den Plattenrand verbiegen und
verdrillen, ergeben sich aus der Richtungstranformation
– 4 / 13 –

und
ϕr � r � ϕ�
– 4 / 14 –
(4.32.1)
ϕ t � t � ϕ� . (4.32.2)
X 3
u 3
m 12
m 11
q 13
m 21
A 2
Bild 4.6 : Schiefer Plattenrand
s
A 1
A
q 23
m 22
ϕ 2
t
X 2
Drei arbeits–
konforme Paare
r
q 3 ,u 3
m r,ϕ r
m t,ϕ t
ω
Plattenrand R
Zwei gleich–
wertige Paare
ϕ 1
q* 3 ,u 3
m r,ϕ r
Für die Durchbiegung u 3 entfällt die Richtungstransformation, da sie auch auf dem
Rand immer senkrecht zur Plattenmittelfläche wirkt. Für die Randmomente ist eine
Orts– und Richtungstransformation durchzuführen. In Analogie zu den Scheibenkräften
gilt für das Randbiegemoment
mr � r�r � m ��
und für das Randtorsionsmoment
X 1
(4.33.1)
m t � r�t � m �� . (4.33.2)
Für die Randquerkraft
q 3 � r � q �3
(4.34)
ist dagegen nur eine Ortstransformation erforderlich. Die Richtung ist wie bei der Durchbiegung
u 3 durch die Plattennormale fest vorgegeben.

Eine Bilanz über die Anzahl der Randgrößen verdeutlicht, daß am Plattenrand drei
arbeitskonforme Paare auftreten. Es sind demnach sechs Randbedingungen zu er–
füllen. Dies steht allerdings im direkten Widerspruch zum vorliegenden Integrations–
problem von 4–ter Ordnung. Die Annahme der Schubstarrheit beeinflußt also neben
den Gebietsgleichungen auch die Randbedingungen. Von den drei auftretenden Randpaaren
ist daher ein Paar gleichwertig durch zwei verbleibende Paare zu ersetzen, vgl.
(Bild 4.6).
Dies gelingt, wenn man das Randtorsionsmoment m t entlang der Randkoordinate s
in Kräftepaare auflöst und zusammen mit der Randquerkraft q 3 die Ersatzquer–
kraft q* 3 bildet. Dieser Vorgang ist im (Bild 4.7) veranschaulicht.
t
∆s
q 3 – ∆q 3
a) Einzelwirkung von q 3 in drei benachbarten Randabschnitten ∆s
t
b) Einzelwirkung von m t in drei benachbarten Randabschnitten ∆s
t
t/2
t/2
t/2
t/2
t/2
t/2
∆s ∆s
∆s ∆s ∆s
m t – ∆m t
q 3 q 3 + ∆q 3
m t
∆s/2
q* 3
m t + ∆m t
∆s/2
c) Resultierende Wirkung von q* 3 im verschobenen Randabschnitt ∆s
Bild 4.7 : Bildung der Ersatzquerkraft
In drei benachbarten Randabschnitten ∆s ist jeweils die Einzelwirkung von q 3 im
(Bild 4.7a) und die Einzelwirkung von m t im (Bild 4.7b) dargestellt. Die Zusammenfassung
im verschobenen Randabschnitt ∆ zur resultierenden Größe q* 3 ist (Bild 4.7c)
zu entnehmen. Es gilt
– 4 / 15 –
s
s
s

q* 3 �s � �q 3 � �q 3��s
2
� q3�s 2 � �mt � �m ��s t
�
�s
mt�s �s
Durch Kürzen von ∆s , Vernachlässigung von Gliedern höherer Ordnung und Bildung
des Grenzübergangs (∆s → 0) folgt
q* 3 � q 3 � �m t
�s � q3 � m t,t . (4.35)
Eine Festlegung von ϕ t entfällt. Die tangentiale Randverdrehung ist durch
ϕ t � t � ϕ� ��t � u 3,� ��u 3,t
– 4 / 16 –
.
(4.36)
eindeutig bestimmt, wobei sich Gl. (4.36) durch Einsetzen von Gl. (4.18) in Gl. (4.32.2)
ergibt. Auf dem Rand von schubstarren Platten sind demnach lediglich die arbeitskonformen
Paare (q* 3 , u 3) und (m r, ϕ r) zu beachten, vgl. (Bild 4.6). Damit lassen sich genau
vier Randbedingungen formulieren, um die Grundgleichungen der schubstarren Plattentheorie
in eindeutiger Form zu integrieren. Für geometrische Randbedingungen auf
dem Weggrößenrand R W gilt
u 3
ϕr
=
u 3
ϕr
und für statische Randbedingungen auf dem Kraftgrößenrand R K
q* 3
mr
=
q 3
mr
.
(4.37.1)
(4.37.2)
Erfolgt die Vorgabe der überstrichenen Größen zu Null, liegen homogene, ansonsten
inhomogene Randbedingungen vor.
Bei Plattentragwerken, die im Grundriß eine unregelmäßige Berandung aufweisen,
stoßen in der Regel zwei schiefe Ränder zusammen, so daß schiefe Ecken entstehen.
Diese Situation ist im (Bild 4.8) dargestellt. (Bild 4.8a) zeigt die Situation im Grund–
riß und (Bild 4.8b) im Seitenriß einer schiefen Ecke. Am Ende des ersten Randes
wirkt im Abschnitt ∆s 1 das resultierende Torsionsmoment (m t1∆s 1) auf den Platten–
rand ein und am Anfang des zweiten Randes im Abschnitt ∆s 2 das resultierende
Torsionsmoment (m t2∆s 2) . Das abschnittsweise Erfassen als Kräftepaare ergibt ver–
tikale Kraftkomponenten, für den Rand 1 ±(m t1∆s 1) / ∆s 1 = m t1 und für den Rand 2
±(m t2∆s 2) / ∆s 2 = m t2 . Die Kraftkomponenten in den inneren Abschnitten der einzelnen
Ränder heben sich gegenseitig auf, vgl. (Bild 4.7b). Im unmittelbaren Bereich der Ecken
kommt es dagegen zu einer Summation der anteiligen Kraftkomponenten, die zusammen
die Eckkraft
A � m t1 � m t2
bilden. Sie ist bei schubstarren Platten zusätzlich zu beachten.
(4.38.1)

X 2
Ecke (6,1)
a) Unregelmäßig berandeter Plattengrundriß
Rand 1
Rand 5
Ecke (5,6)
Rand 6
Rand 1
∆s1
Ecke (1,2)
∆s1
m t1
b) Seitenriß der schiefen Ecke (1,2)
Ecke (4,5)
Rand 2
Bild 4.8 : Platte mit schiefen Rändern und Ecken
A
∆s2
m t2
Ecke (1,2)
– 4 / 17 –
Rand 4
∆s2
Ecke (3,4)
Rand 3
Ecke (2,3)
Rand 2
Wenn zwei freie und damit auch kraftfreie Ränder zusammenstoßen, ist die Eckkraft
Gl. (4.38.1) Null. Bei volleingespannten Plattenrändern, die in einer Ecke zusammenstoßen,
stellt sich ebenfalls keine Eckkraft ein. Wegen u 3,t = 0 gilt u 3,tt = 0 und damit
auch m t = 0. Bei gelenkiger Lagerung der Plattenränder ist zwischen zwei Fällen zu unterscheiden.
Bei einer Lagerung ohne Zugverankerung heben die Plattenränder in den
Ecken ab und entziehen sich somit der Kraftaufnahme. Durchbiegung und Momente in
Plattenmitte werden größer. Dies ist bei der Bemessung der Platte zu berücksichtigen.
Ist dagegen eine Zugverankerung zur Aufnahme der Eckkraft vorgesehen, z.B. durch
aufliegendes Mauerwerk, treten in den Ecken Torsionsmomente auf, die zur Eckkraft
Gl. (4.38.1) führen. Speziell für rechtwinklige Ecken ergibt sich der Wert
A � m 12 � m 21 � 2m 12 . (4.38.2)
In diesem Fall ist in den Ecken eine Bewehrung zur Aufnahme der Torsionsmomente
vorzusehen.
X 1

4.5 Lösungswege der Plattentheorie
Im Rahmen der Scheibentheorie wurden drei mögliche Lösungswege vorgestellt, die
von grundsätzlich unterschiedlichen Formulierungen der Integrationsgleichungen ausgehen.
1. Die gemischte Formulierung in Weg– und Kraftgrößen.
2. Die Gleichgewichtsformulierung in Weggrößen.
3. Die Verträglichkeitsformulierung in Kraftgrößen.
Die klassische Scheibengleichung ∆∆F = 0 beruht auf der dritten Lösungsvariante. Dagegen
hat sich im Rahmen der klassischen Plattentheorie die zweite Variante bewährt.
Sie führt auf die Plattengleichung
��u 3 � p3
B
, (4.39)
die in ihrer Struktur vollständig mit der Balkengleichung
w���� � p
EI
übereinstimmt. Die Operatoren
und
� � ( ) ,11 � ( ) ,22
�� � � 2 � ( ) ,1111 � 2( ) ,1122 � ( ) ,2222 ,
die in Gl. (4.39) auftreten, wurden bereits bei der Ableitung der Scheibengleichung
durch Gl. (3.42) definiert, vgl. Teil 3: Scheibentheorie. p 3 ist die Flächenlast Gl. (4.3)
und B die Plattensteifigkeit Gl. (4.24). Die explizite Form der Plattengleichung (4.39)
ergibt sich, wenn man Gl. (4.30) nach den Momenten auflöst,
m �� ��BE ���� u 3,�� . (4.40)
oder ausgeschrieben
und
m 11 ��B�u 3,11 � �u 3,22 � , (4.40.1)
m 22 ��B��u 3,11 � u 3,22 � (4.40.2)
m 12 ��B(1 � �)u 3,12 � m 21 ,
– 4 / 18 –
(4.40.3)
das Ergebnis der Invertierung unter Beachtung konstanter Materialwerte in Gl. (4.28)
einsetzt und die Operatoren Gl. (3.42) einführt.

4.6 Lösungsmethoden der Plattentheorie
Der mathematische Aufwand ist sehr groß, um die Plattengleichung (4.39) analytisch
zu integrieren. Dies gelingt in der Regel auch nur für einfache Geometrien, Einwirkungen
und Randbedingungen. Näherungslösungen mit dem Ritz–Verfahren kann man
dagegen mit relativ geringem Aufwand ermitteln. Dies gilt aber wiederum nur für ein–
fache Geometrien, Einwirkungen und Randbedingungen. Wenn es darum geht, baupraktische
Plattenprobleme zu lösen, sind vor allem die Gitterrostmethode und die Methode
der finiten Elemente von Interesse, die im Teil 6 und 7 u.a. auch im Zusammenhang
mit der Anwendung auf Plattentragwerke betrachtet werden.
Die analytische Integration und das Ritz–Verfahren sind ausführlich in /1/, /3/ und /5/
behandelt. Eine kurze Diskussion der jeweiligen Vorgehensweise soll die theoretischen
Grundlagen dieser Methoden verdeutlichen. Die praktische Anwendung des Ritz–Verfahrens
anhand eines Beispiels erfolgt im Abschnitt 4.7.
4.6.1 Analytische Integration der Plattengleichung
Die Plattengleichung (4.39) wird im Zusammenhang mit dem Beispiel der allseitig gelenkig
gelagerten Rechteckplatte integriert, auf die eine konstante Teilflächenlast einwirkt.
Die Teilflächenlast ist durch den Aufpunkt (u, v) festgelegt. Die vollständigen Berechnungsdaten
sind (Bild 4.9) zu entnehmen.
v
d
d
X 2
p 3 ,u 3
p 3 ,u 3
u
Lastaufpunkt
L 1 = a
c c
Bild 4.9 : Gelenkig gelagerte Rechteckplatte
– 4 / 19 –
p 3 = konstant
X 1
X 1
X 2
p 3 = konstant
p 3 ,u 3
Dicke
E–Modul
Querdehnzahl
L 2 = b
: t
: E
: ν

Gesucht sind die Verläufe der Durchbiegung u 3 = u 3(X 1 , X 2 ) der Momente
m αβ = m αβ (X 1 , X 2 ) und der Hauptmomente m r1 und m r2 . Die Auswertung soll für den
Sonderfall der Quadratplatte unter voller Flächenlast erfolgen.
Die geometrische Randbedingung u 3 = 0 und die statische Randbedingung m r = 0
ist auf allen vier Rändern zu erfüllen. Auf den Rändern X 1 = 0 und X 1 = a gelten für
die Komponenten des Randnormalenvektors r die Werte r 1 = �1 und r 2 = 0 und
auf den Rändern X 2 = 0 und X 2 = b die Werte r 1 = 0 und r 2 = �1. Mit Gl. (4.33.1)
folgt daraus unmittelbar, daß auf den X 1 –Rändern m r = �m 11 gilt und auf den
X 2 – Rändern m r = �m 22 . Auf den X 1 –Rändern ist wegen u 3 = 0 auch u 3,2 = 0 und
damit auch u 3,22 = 0 . Aus m r = �m 11 = �B u 3,11 = 0 folgt zusätzlich u 3,11 = 0 , so daß
man hier die Randbedingung m r = 0 durch die Bedingung u 3,11 + u 3,22 = ∆u 3 = 0 ersetzen
kann. Auf den X 2 –Rändern kann man ebenfalls die Randbedingung m r = 0 durch
die Bedingung ∆u 3 = 0 ersetzen. Hier gilt wegen u 3 = 0 auch u 3,1 = 0 und u 3,11 = 0
und wegen m r = �m 22 = �B u 3,22 = 0 zusätzlich auch u 3,22 = 0.
Die analytische Integration beruht auf dem Doppelreihen–Sinusansatz
mit
und
u 3 �X 1 ,X 2� � � � u 3mn sin�mX 1 sin�nX 2 (4.41)
�m � m�
a
�n � n�
b
– 4 / 20 –
(4.41.1)
. (4.41.2)
Dieser Ansatz ist zulässig, da er die Randbedingungen u 3 = 0 und ∆u 3 = 0 auf allen
Rändern identisch erfüllt. Entwickelt man die Flächenlast p 3 = p 3 (X 1 , X 2 ), die auf der
rechten Seite der Plattengleichung steht, nun ebenfalls in eine doppelte Sinusreihe, ist
ein Koeffizientenvergleich zwischen Lösungs– und Lastansatz möglich, um die unbekannten
Koeffizienten u 3mn im Lösungsansatz Gl. (4.41) zu ermitteln.
Die Entwicklung der Flächenlast in eine doppelte Sinusreihe ist durch eine Fourier–
Reihe grundsätzlich immer möglich. Es gilt
p ~ 3 �X 1 ,X 2� � � � p 3
mn sin�mX 1 sin�nX 2 . (4.42)

Die Lastentwicklung Gl. (4.42) ist mit dem Kopfzeiger (�) gekennzeichnet, um sie von
der vorgegebenen Lastfunktion p3 zu unterscheiden. Beide Funktionen stimmen überein,
wenn die Summation in Gl. (4.42) über ausreichend viele Reihenglieder erfolgt. Die
Fourier–Koeffizienten p 3
mn in der Lastentwicklung Gl. (4.42) sind durch den Integralausdruck
p 3
mn �
4
ab �u�c
u�c
v�d
�
v�d
p 3 �X 1 ,X 2� sin � m X 1 sin � n X 2 dX 1 dX 2
– 4 / 21 –
(4.43)
definiert. Mit p 3 = konstant ergibt die Auswertung des Doppelintegrals Gl. (4.43) den
Wert
p 3 16p3
mn �
�2mn sin�mu sin�mc sin�nv sin�nd . (4.44)
Setzt man nun den Reihenansatz Gl. (4.41) und die Lastentwicklung Gl. (4.42) in die
Plattengleichung (4.39) ein, so erhält man durch Koeffizientenvergleich den Ausdruck
u 3mn �
p 3
mn
B��2 m � �2 . (4.45)
�2
n
Bei voller Last liegt der Lastaufpunkt (u, v) in der Mitte der Platte. Dann ist u = c = a/2
und v = d = b/2 , vgl. (Bild 4.8) und aus Gl. (4.44) folgt
p 3 16p3
mn �
�2mn , (m, n) � 1, 3, 5 ... . (4.46)
Damit ist die Lösung für die Durchbiegungsfunktion einer Rechteckplatte bei voller
Lasteinwirkung bekannt. Setzt man Gl. (4.46) in Gl. (4.45) und Gl. (4.45) in Gl. (4.41)
ein, so erhält man den Ausdruck
u 3 �X 1 ,X 2� � 16p3
B� 2 � m
� n
sin� mX 1 sin� nX 2
mn�� 2 m � �2 n �2
. (4.47)
Mit Gl. (4.47) sind auch die Schnittmomente bekannt. Bildet man die zweiten partiellen
Ableitungen von Gl. (4.47) und setzt sie in Gl. (4.39.1 bis 3) ein, so ergeben sich die
Ausdrücke
m 11�X 1 ,X 2� � 16p3
� 2 � m
m 22�X 1 ,X 2� � 16p3
� 2 � m
� n
� n
�� 2 m � ��2 n �sin�mX 1 sin�nX 2
mn�� 2 m � �2 n �2
�� 2 n � ��2 m �sin�mX 1 sin�nX 2
mn�� 2 m � �2 n �2
, (4.48.1)
(4.48.2)

und
m 12�X 1 ,X 2� ��(1 � �) 16p3
� 2 � m
� n
� m� ncos� mX 1 cos� nX 2
mn�� 2 m � �2 n �2
– 4 / 22 –
� m 21�X 1 ,X 2� . (4.48.3)
Die Summation in Gl. (4.47) und Gl. (4.48) ist wegen Gl. (4.46) nur mit den ungeraden
Gliedern (m, n) = 1, 3, 5 ... der Fourier–Reihenentwicklung Gl. (4.42) auszuwerten.
Die Hauptmomente berechnen sich aus der Bedingung, daß die Torsionsmomente m t
in den Linienschnitten der Hauptrichtungen verschwinden. Bei Flächentragwerken
treten zwei Hauptrichtungen auf, die einen Winkel von 90° einschließen. Sie sind im
(Bild 4.10) dargestellt.
X 2
m t2 = 0
m r2
Haupt–
richtung 2
ω 2
ω 1
Haupt–
richtung 1
Bild 4.10 : Hauptmomente von Platten
m r1
m t1 = 0
Momente in Linienschnitten sind wie Randmomente zu bilden. Für das Torsionsmoment
im beliebigen Linienschnitt erhält man daher unter Beachtung von Gl. (4.33.2) und
Gl. (3.28) den Ausdruck
m t � r�t � m �� , (4.49)
� r 1 t 1 m 11 � r 2 t 2 m 22 � r 1 t 2 m 12 � r 2 t 1 m 21 ,
� sin�cos��� m 11 � m 22� � m 12�cos 2 � � sin 2 �� .
ω 1
X 1

Das Umformen von Gl. (4.49) mit Hilfe von Additionstheoremen, das m t = 0 setzen und
die Auflösung nach dem Winkel ω ergibt die Lage der ersten Hauptrichtung.
tan2� 1 �
2m12
m11 .
� m22 Die Lage der zweiten Hauptrichtung ist dann durch
� 2 � � 1 � 90°
bekannt, vgl. (Bild 4.10).
– 4 / 23 –
(4.50.1)
(4.50.2)
Für das Biegemoment im beliebigen Linienschnitt erhält man unter Beachtung von
Gl. (4.33.1) und Gl. (3.28) den Ausdruck
mr � r�r � m �� , (4.51)
� r 1 r 1 m 11 � r 2 r 2 m 22 � r 1 r 2 m 12 � r 2 r 1 m 21 ,
� cos 2 �m 11 � sin 2 �m 22 � 2sin�cos�m 12 .
Die Hauptmomente m r1 und m r2 folgen nun aus Gl. (4.51), wenn man jeweils die Winkel
Gl. (4.50.1) und Gl. (4.50.2) einsetzt. Alternativ kann man die Hauptmomente auch
mit der Gleichung
m r1,2 � m11 � m 22
2
�
�
�m11 � m22� 2
2
2
� �m12� (4.52)
berechnen. Sie ergibt sich, wenn man Gl. (4.49) und Gl. (4.51) durch Umformen mit Hilfe
von Additionstheoremen, Quadrieren und Addieren zusammenfaßt, m t = 0 setzt und
dann durch Wurzelziehen die Hauptmomente ermittelt.
Im (Bild 4.11) ist die analytische Lösung für eine Quadratplatte mit den Spannweiten
L 1 = a und L 2 = b = a und der Querdehnzahl ν = 0.3 ausgewertet. Im (Bild 4.11a) ist
der Verlauf der Durchbiegungsfunktion Gl. (4.47) dargestellt. Zur Berechnung des maximalen
Wertes in Plattenmitte sind acht Reihenglieder erforderlich, damit sich die ersten
drei Ziffern nicht mehr ändern. Für die Momente ist die Konvergenz schlechter. Es sind
bereits 14 Reihenglieder erforderlich, um die angestrebte Genauigkeit bis zur dritten
Ziffer zu erreichen. Die Verläufe der auf die X 1 – und X 2 –Koordinaten bezogenen Momentenfunktionen
Gl. (4.48) sind im (Bild 4.11b) und die Verläufe der Hauptmomente
Gl. (4.52) im (Bild 4.11c) dargestellt.
Auf den Symmetrielinien (X 1 = L 1/2 = a/2, X 2 ) und (X 1 , X 2 = L 2/2 = a/2) in der Mitte
der Platte verschwinden die Torsionsmomente. Dann stimmen nach Gl. (4.52) die
Hauptmomente in Plattenmitte mit den Biegemomenten überein. Im einzelnen gilt:
m r1 = m 11 und m r2 = m 22 . Auf den Plattenrändern treten wegen der gelenkigen Lagerung
keine Biegemomente sondern nur Torsionsmomente auf, die in den Ecken maximale
Werte erreichen. Dann stimmen nach Gl. (4.52) die Hauptmomente in den
Plattenecken mit den Torsionsmomenten überein. Im einzelnen gilt: m r1 = m 12 und
m r2 = – m 12 . Gl. (4.50.1) ist wegen tan2ω 1 = ∞ → 2ω 1 = 90° zu entnehmen, daß m r1

a/2
a/2
a) Durchbiegung u 3
A
m 12
A
b) Momente und Eckkräfte
–
X 2
+
–
+
–
a/2 a/2
m 22
L 1 = a
0.00406 p3 a 4
B
c) Hauptmomente entlang einer Diagonalen
+
+
m r2
+
m 21
0.0479p 3 a 2
m 21
m 11
0.0325p 3 a 2
Bild 4.11 : Gelenkig gelagerte Quadratplatte unter voller Flächenlast
–
+
+ –
m r1
0.0479p 3 a 2
– 4 / 24 –
–
L 2 = a
A
m 12
0.0325p 3 a 2
X 1
0.0325p 3 a 2
A = 0.065p 3 a 2
0.0325p 3 a 2
m r2
m 22
m r1
p 3 ,u 3
m 21 = m 12
m 11
m 12

die Platte unter ω 1 = 45° beansprucht und Gl. (4.50.2) ist zu entnehmen, daß m r2 die
Platte unter ω 2 = 135° beansprucht, vgl. (Bild 4.10). Für die Verteilung in Richtung der
Diagonalen verhalten sich die Ecken wie feste Einspannungen, vgl. (Bild 4.11c). Dies
setzt aber voraus, daß die Verankerung der Eckkräfte Gl. (4.38.2) durch geeignete konstruktive
Maßnahmen erfolgt, um das Abheben der Plattenränder von der Lagerung zu
verhindern. Der Durchbiegungsverlauf entlang der Diagonalen muß im Randbereich
Wendepunkte der Krümmung aufweisen, vgl. (Bild 4.11a).
4.6.2 Ritz–Verfahren
Das Ritz–Verfahren beruht auf einer schwachen Formulierung der Gleichgewichtsbedingung
Gl. (4.28) Mit dem PvW ist im Gebiet G der Plattenmittelfläche die virtuelle
Arbeit
W v � � G
u v 3�m ��
,�� � p3�dG � 0
– 4 / 25 –
(4.53)
zu bilanzieren, um das Kräftegleichgewicht von schubstarren Platten in schwacher
Form zu erhalten. In Gl. (4.53) ist u v 3 � uv 3 (X1 ,X 2 ) eine virtuelle Durchbiegungsfunktion,
die mit der wirklichen Kräftesumme �m ��
,�� � p3� einen arbeitskonformen Ausdruck bildet.
Sie ist als virtuelle Größe beliebig. Gl. (4.53) kann daher nur erfüllt sein, wenn der
Klammerausdruck der Kräftesumme verschwindet, der dann mit der Differentialgleichung
(4.28) übereinstimmt. Gl. (4.53) muß zusätzlich die statischen Randbedingungen
Gl. (4.37.2) erfüllen. Dies ist auch an der Stellung der zwei partiellen Ableitungen
zu erkennen, die beide bei einer statischen Größe, nämlich dem Moment stehen.
Mit der Identität
�
G
�u v 3 m�� ,� � ,� dG � � G
und der partiellen Integration
�
G
q �3 q 3
�u v 3 m�� ,� � ,� dG � � R
u v 3,� m�� ,� dG �� G
u v 3 q�3 r � dR � � R
u v 3 m��
,�� dG
u v 3 q3 dR ,
die unter Beachtung von Gl. (4.27) und Gl. (4.34) erfolgt, erhält man als erste Umformung
den Ausdruck
�
G
u v 3 m��
,�� dG � � R
u v 3 q3 dR �� G
uv 3,�m�� ,�dG . (4.54)

Mit der Identität
���u G
v 3,�m��� dG ���
,�
G
und der partiellen Integration
�� G
� ϕ v �
�u v 3,� m��� ,� dG �� R
u v 3,�� m�� dG �� G
m �
ϕ v � m�� r�dR � � R
– 4 / 26 –
u v 3,� m�� ,� dG
ϕ v � m� dR � � R
�ϕ v r mr � ϕ v t m t �dR ,
die unter Beachtung von Gl. (4.18), Gl. (4.32) und Gl. (4.33) erfolgt, erhält man als
zweite Umformung den Ausdruck
�� G
u v 3,� m�� ,� dG � � R
�ϕ v r mr � ϕ v t m t �dR �� G
u v 3,�� m�� dG . (4.55)
Gl. (4.55) in Gl. (4.54) eingesetzt, ergibt für die erste und zweite Umformung den Ausdruck
�
G
uv 3m�� ,�� dG � ��u R
v 3q3 � ϕv r mr � ϕv t mt�dR ��
G
u v 3,�� m�� dG , (4.56)
der eine Vertauschung der Ableitungen von den wirklichen Momenten zur virtuellen
Durchbiegung bewirkt. Mit Gl. (4.56) kann man Gl. (4.53) gleichwertig durch
W v � � G
u v 3,�� m�� dG �� G
u v 3 p3 dG �� R
�u v 3 q3 � ϕ v r mr � ϕ v t m t �dR � 0
(4.57)
ersetzen. Gl. (4.57) muß zusätzlich geometrische Randbedingungen für die virtuellen
Größen erfüllen, weil durch die Umformung die zwei partiellen Ableitungen von den
wirklichen Momenten zur virtuellen Durchbiegung wechseln. Im Randintegral von
Gl. (4.57) treten aber noch drei arbeitskonforme Paare auf. Es ist daher eine weitere
Umformung erforderlich, um sie durch zwei gleichwertige Paare zu ersetzen, vgl.
(Bild 4.6). Mit Gl. (4.18) und Gl. (4.32.2) kann man die tangentiale Randverdrehung
durch
ϕ v t � t� ϕ v � ��t � u v 3,� ��uv 3,t
(4.58)
ausdrücken. Gl. (4.58) in das Randintegral von Gl. (4.57) eingesetzt, ergibt den Ausdruck
��u v 3 q3 � ϕrmr � u v 3,t m t �dR . (4.59)

Mit der Identität
���u R
v 3mt� ,t dR ��� R
u v 3,t m t �� R
u v 3,t m t,t dR
und der partiellen Integration
���u R
v 3mt� ,t dR ��uv 3 �mt1 � m � t2 ,
Ecke
erhält man als dritte Umformung den Ausdruck
�� uv 3,tmtdR ��uv 3 �mt1 � m � t2 �� u
Ecke v 3mt,tdR . (4.60)
Gl. (4.60) in Gl. (4.59) eingesetzt, ergibt für das Randintegral von Gl. (4.57) einen Ausdruck,
in dem nur noch zwei konjugierte Paare auftreten, wenn man die Ersatzquerkraft
Gl. (4.35) und die Eckkraft Gl. (4.38.1) als neue Unbekannte einführt.
��u v 3 q* 3 � � v r mr�dR � �u v 3 A� Ecke . (4.61)
Die statischen Randbedingungen Gl. (4.37.2) gelten auf dem Kraftgrößenrand R K . Sie
sind natürlich erfüllt, da das Moment in Gl. (4.57) keine Ableitung mehr trägt. Im homogenen
Fall gilt q* 3 = 0, m r = 0 und A = 0 , so daß Gl. (4.61) entfällt. Dagegen sind im
inhomogenen Fall die Arbeitsanteile von bekannten Einwirkungen q* 3 = q 3 , m r = m r und
ggf. A = A mit Hilfe von Gl. (4.61) zu erfassen.
Die geometrischen Randbedingungen Gl. (4.37.1) sind auf dem Weggrößenrand R W
zu erfüllen. Die virtuellen Weggrößen u v 3 und ϕv r müssen auf R W verschwinden, um
zu erreichen, daß Gl. (4.61) ebenfalls entfällt. Dies ist der Fall, wenn man die virtuellen
Weggrößen als Änderungen der wirklichen Weggrößen definiert. Es gilt
u v 3 � �u 3
und mit Gl. (4.32.1) und Gl. (4.18)
– 4 / 27 –
(4.62.1)
ϕ v r � �ϕr � r � �ϕ� ��r � �u 3,� ���u 3,r . (4.62.2)
Gibt man nun die geometrischen Randbedingungen für die wirklichen Weggrößen vor,
dann sind durch Gl. (4.62) auch die geometrischen Randbedingungen der virtuellen
Weggrößen erfüllt, so daß der Randterm Gl. (4.61) vollständig aus dem virtuellen Arbeitsausdruck
Gl. (4.57) entfällt. Es verbleiben lediglich die Gebietsintegrale der inneren
und äußeren Arbeit.
�W � � G
�u 3,�� m �� dG �� G
�u 3 p 3 dG � 0 . (4.63)

Die Momente im inneren Arbeitsanteil von Gl. (4.63) können durch die Verträglichkeitsaussage
Gl. (4.40) eliminiert werden.
�W � � G
�u 3,�� �BE �����u 3,�� dG �� G
�u 3 p 3 dG � 0 . (4.64)
Mit Gl. (4.64) ist die endgültige Form des PvW für schubstarre Platten bekannt. Das
Prinzip ist eine notwendige Bedingung dafür, daß die gesamte potentielle Energie Π
einen minimalen Wert annimmt, wenn der gesuchte Gleichgewichtszustand vorliegt.
� � 1
2 � G
BE ���� u 3,�� u 3,�� dG �� G
u 3 p 3 dG � Minimum . (4.65.1)
In Gl. (4.65.1) erfaßt der erste Term die im Plattentragwerk gespeicherte Formänderungsenergie
und der zweite Term das Potential der Einwirkungen. Das Ausschreiben
von Gl. (4.65.1) ergibt den Ausdruck
� � 1
2 � G
�� G
B��u3,11 � u � 3,22 2
� 2(1 � �) �u3,11u3,22 � �u � 3,12 2��dG
u 3 p 3 dG � Minimum .
– 4 / 28 –
(4.65.2)
Das Ritz–Verfahren zur Berechnung von schubstarren Platten beruht auf Gl. (4.65.2).
Alle Funktionen
u 3 � � Cnfn�X 1 ,X 2� ,n�1,2,3 ...
(4.66)
mit zweiten partiellen Ableitungen ungleich Null sind zur Konkurenz zugelassen, wenn
sie die geometrischen Randbedingungen Gl. (4.37.1) als Zwangsbedingungen erfüllen.
Die statischen Randbedingungen Gl. (4.37.2) unterliegen dagegen keinen Zwängen.
Sie sind implizit als natürliche Bedingungen in Gl. (4.65.2) enthalten.
4.7 Beispiel zum Ritz–Verfahren
Mit dem Ritz–Verfahren soll die Mittendurchbiegung einer quadratischen Platte berechnet
werden. Das Berechnungssystem ist im (Bild 4.9) dargestellt. Die konstante
Flächenlast erstreckt sich über die gesamte Mittelfläche der Platte. Das Ergebnis der
analytischen Integration ist (Bild 4.11a) zu entnehmen.

Als Ritzansatz Gl. (4.66) kann man z.B. den Doppelreihen–Sinusansatz Gl. (4.41) der
analytischen Integration wählen und mit Hilfe von Gl. (4.65.2) die unbekannten Koeffizienten
u 3mn der dominanten Reihenglieder berechnen. Durch diese spezielle Wahl
stimmt das Ergebnis des Ritz–Verfahrens mit dem Ergebnis der analytischen Integration
Gl. (4.45) überein.
Als alternative Ritzansätze Gl. (4.66) sind aber auch Ansätze zulässig, die nicht mit der
analytisch exakten Integration der Plattengleichung übereinstimmen. Allerdings sind
zwei Kriterien bei der Konstruktion von zulässigen Näherungsansätzen zu beachten:
1. Die Ansätze sind so zu wählen, daß die zweiten partiellen Ableitungen in Richtung
der X 1 – und X 2 –Koordinaten mindestens konstante Werte ergeben. Dies ist erforderlich,
um als minimale Voraussetzung konstante Krümmungen zu erfassen.
2. Die Ansätze sind so zu wählen, daß sie die geometrischen Randbedingungen des
Problems nicht verletzen.
Der eingliedrige Polynomansatz
u 3 � C�X 1�X 1 � L 1 � X 2�X 2 � L 2 ��
erfüllt bereits beide Voraussetzungen. Die partiellen Ableitungen
und
u 3,11 � �u 3
�X 1 �X 1 � 2C�X 2�X 2 � L 2 �� ,
u 3,22 � �u 3
�X 2 �X 2 � 2C�X 1�X 1 � L 1 ��
u 3,12 � �u 3
�X 1 �X 2 � C��2X 1 � L 1 ��2X 2 � L 2 ��
ergeben Werte ungleich Null und die geometrischen Randbedingungen der gelenkig
gelagerten Ränder
und
X 1 � 0 � u 3 � 0,
X 1 � L 1 � u 3 � 0,
X 2 � 0 � u 3 � 0
X 2 � L 2 � u 3 � 0
– 4 / 29 –

sind ebenfalls erfüllt. Unbekannte des Näherungsansatzes ist die Konstante C , die zusätzlich
noch Gl. (4.65.2) erfüllen muß. Um dies zu erreichen, sind erstens der Näherungsansatz
und die partiellen Ableitungen davon in Gl. (4.65.2) einzusetzen und zweitens
die Gebietsintegrale auszuwerten. Als Ergebnis erhält man den Ausdruck
� � 1
2 C2� �
�
� C� �
�
4B� �
�
�L � 1 5 L2 30 � L1�L � 2 5
p 3 �L 1 � 3 �L 2 � 3
36
� �
�
30 � �L 1 � 3 �L 2 � 3
� Minimum,
– 4 / 30 –
18 ��
� ��
�
der nur noch von der Konstanten C abhängt. Die Anwendung des PvW Gl. (4.64) als
notwendige Bedingung der Lösung führt auf
�� � ��
�C � 0.
�C
Die virtuelle Größe δC ist beliebig. Dann muß ��
�C
zu erfüllen.
��
�C
� C� �
�
�� �
�
4B� �
�
�L � 1 5 L2 30 � L1�L � 2 5
p 3 �L 1 � 3 �L 2 � 3
36
� �
�
Die Auflösung nach C ergibt
C � 1
24
�
��
�
�
�
�
�L 1 � 2 �L 2 � 2
��L � 1 4
5 � �L � 2 4
30 � �L 1 � 3 �L 2 � 3
� 0.
5 � �L � 1 2 �L � 2 2
3
� p3
B
�
��
�
�
�
�
und speziell für Qudratplatten mit L 1 = L 2 = a
C � 15
264
p 3
B .
18 ��
� ��
�
gleich Null werden, um das PvW
Damit ist eine Näherungslösung für die Durchbiegungsfunktion u 3 = u 3(X 1 ,X 2 ) bekannt.
Die Auswertung in Plattenmitte mit X 1 = L 1 / 2 = a / 2 und X 2 = L 2 / 2 = a / 2 ergibt den
Wert
u 3,Mitte � 0.00355 p3 a 4
B ,

der kleiner ausfällt als der Wert der analytisch exakten Lösung im (Bild 4.11a). Die Abweichung
beträgt 12.6 %. Zur Abschätzung der Größenordnung ist dies eine noch ausreichende
Genauigkeit. Sie reicht aber nicht mehr aus, wenn man zusätzlich auch noch
die Größenordnung der Momente abschätzen will. Die Auswertung von Gl. (4.40.1) und
Gl. (4.40.2) in Plattenmitte ergibt für die Biegemomente den Wert
m11 � m22
Mitte Mitte � 0.0369p3a2 ,
der nun doch schon deutlich kleiner ausfällt als der Wert der analytisch exakten Lösung
im (Bild 4.11b). Die Abweichung beträgt bereits 23 %. Die Torsionsmomente in den
Ecken der Platten fallen dagegen größer aus als die Vergleichswerte der analytischen
Integration im (Bild 4.11b). Die Auswertung von Gl. (4.40.3) ergibt den Wert
m 12
Ecken �� 0.0398p3 a 2 .
Die Abweichung beträgt 22.5 %. Die Genauigkeit des Ritz–Verfahrens läßt sich aber
in einfacher Weise dadurch erhöhen, indem man die Berechnung mit verbesserten
Näherungsansätzen durchführt. Dies ist in zweierlei Weise möglich. Der klassische
Weg besteht darin, in Gl. (4.66) höherwertige Verlaufsfunktionen f n(X 1 , X 2 ) zu verwenden,
um die Anzahl der unbekannten Parameter C n und damit die Anzahl der algebraischen
Gleichungen so gering wie möglich zu halten. Der moderne Weg beruht dagegen
auf der umgekehrten Vorgehensweise, da die Anzahl der anfallenden Gleichungen im
Zeitalter von Rechnern keine Rolle mehr spielt.
Die Konstruktion von einfachen Verlaufsfunktionen, die im gesamten Gebiet der Plattenmittelfläche
gelten, ergibt keinen Sinn, wenn es um die Erhöhung der Genauigkeit
geht. Löst man dagegen die gesamte Plattenmittelfläche in endlich viele Teilflächen auf,
kann man in einfacher Weise Verlaufsfunktionen konstruieren, die für alle Teilflächen
gelten. Die Anzahl der unbekannten Parameter C n der Teilflächenansätze sind die
Variablen des Problems. Das Zusammensetzen der endlich vielen Teilflächen gelingt
mit Hilfe der geometrischen Randbedingungen. Sie sind nun als Übergangsbedingungen
zwischen den einzelnen Teilflächen zu formulieren. Dies führt zwar auf sehr viele
Unbekannte C n, Aufbau und Lösung von großen algebraischen Gleichungssystemen
ist aber durch den Einsatz von Rechnern problemlos zu bewältigen und bereitet daher
keine Schwierigkeiten.
Die endlichen Teilflächen werden in allgemeiner Form als finite Elemente bezeichnet.
Das Ritz–Verfahren und die Methode der finiten Elemente sind demnach sehr eng miteinander
verwandt. Sie beruhen auf gleichen theoretischen Grundlagen. Unterschiede
gibt es nur in der Art und Weise der technischen Durchführung. Die spezielle Vorgehensweise
der Methode der finiten Elemente wird im Teil 7 im Detail vorgestellt.
– 4 / 31 –

Teil 5: Schalentheorie
5.1 Einführung
Geometrische Form und Festigkeit bilden bei Schalen (Bild 5.1) eine untrennbare Ein–
heit. Diese Eigenschaft ist besonders deutlich bei den natürlichen Konstruktionen der
Natur zu beobachten, die in der Regel Schalen darstellen. In diesem Zusammenhang
sei z.B. an Schneckenschalen (Bild 5.1a) oder an Muschelschalen, Krebsschalen,
Schildkrötenschalen, Eierschalen usw. erinnert, die sich alle durch eine optimale Festigkeit
bei minimalem Materialeinsatz auszeichnen.
Optimale Festigkeit bzw. optimales Tragverhalten liegt vor, wenn alle Fasern in möglichst
allen Querschnitten der betrachteten Konstruktion eine möglichst gleichmäßige
Beanspruchung erfahren. Dieser Zustand führt unmittelbar zur vollen Ausnutzung des
eingesetzten Materials. Aus physikalischen Gründen kann es nur ein reiner Dehnungszustand
sein, wie er z.B. auch bei Scheiben auftritt. Bei ebenen Flächen kann er sich
aber nur einstellen, wenn man die Richtungen der Einwirkungen einschränkt. Beim statischen
Modell Scheibe dürfen sie daher nur in der Fläche angreifen. Greifen sie dagegen
senkrecht zur Fläche an, ein Fall, wie er z.B. beim statischen Modell Platte auftritt,
stellt sich bei ebenen Flächen ein reiner Biegezustand ein. Dadurch verlagert sich die
Hauptbeanspruchung in die Außenfasern des Querschnitts. Er ist nicht mehr voll ausgenutzt,
was sich besonders bei dünnwandigen Flächentragwerken sehr ungünstig auswirkt.
Platten stellen daher keine optimalen Tragwerke dar.
Will man dagegen erreichen, daß sich auch ohne Einschränkung der Einwirkungsrichtung
ein möglichst reiner Dehnungszustand in Flächentragwerken einstellt, muß man
die Fläche verkrümmen, also die geometrische Form verändern. Der gezielte konstruktive
Eingriff in die Gestaltung der Fläche führt zum statischen Modell Schale (Bild 5.1b),
das zusammen mit den bereits betrachteten statischen Modellen Scheibe und Platte die
Klasse der Flächentragwerke bildet.
Bei Schalen bezeichnet man den reinen Dehnungszustand als Membranzustand. Dies
geschieht in Anlehnung an dünne, vor allem in der Natur auftretende Haut– bzw. Membranstrukturen.
Sie sind völlig biegefrei. Dieser Zustand läßt sich bei technischen Schalen
nur näherungsweise erreichen. Oberstes Ziel beim Entwurf von Schalen sollte es
aber immer sein, Formen zu finden, die Einwirkungen möglichst biegefrei abtragen /14/.
Sonst sind große, i.a. unzulässige Verformungen die zwangsläufige Folge. Reine Biegezustände
sind auf jeden Fall zu vermeiden. Sie werden als dehnungslose Verschiebungen
bezeichnet. Da sie sich diametral zum günstigen Membranzustand verhalten,
sind Schalen, die zu dehnungslosen Verschiebungen neigen, aus ästhetischen und
wirtschaftlichen Gründen immer als Fehlkonstruktion zu bezeichnen.
– 5 / 1 –

a) Schneckenschale
b) Statisches Modell Schale: Überdachung eines Naturtheaters
Bild 5.1: Natürliche und technische Schalen, entnommen aus /14/
– 5 / 2 –

Das optimale Verhalten von gekrümmten Tragwerken war schon den Baumeistern der
Antike bekannt /15/. Zahlreich erhaltene Viadukte und Straßenbrücken, vor allem aber
das Pantheon in Rom sind auch heute noch eindrucksvolle Zeugen von dieser Kenntnis.
Das Pantheon (Bild 5.2), um 130 gebaut, hat z.B. eine Kuppel, die bei einem Durchmesser
von 43.5 m eine Höhe von 40. m erreicht. Bei den genannten Bauwerken handelt
es sich um druckbeanspruchte Konstruktionen aus Naturstein oder Gußwerk, eine
der heutigen Betontechnik verwandten Bauweise. Der Widerstand gegenüber einer
Biegebeanspruchung ist gering.
Gekrümmte Stäbe tragen Lasten biegefrei ab, wenn sie eine speziell geneigte Form aufweisen,
die dazu führt, daß sich das Krafteck allein mit Längskräften schließt. Für den
Bogen ist dieser Zusammenhang im (Bild 5.3) dargestellt.
N links
a) Bogenausschnitt
F = p ⋅ ∆s
�s
N rechts
Bild 5.3 : Biegefreier Gleichgewichtszustand beim Bogen
p
– 5 / 3 –
N links
N rechts
b) Krafteck
Die resultierende Last, die auf dem Bogenausschnitt (Bild 5.3a) einwirkt, ist im Gleichgewicht
mit den unterschiedlich geneigten Längsdruckkräften. Das Krafteck (Bild 5.3b)
ist geschlossen, ohne das Querkräfte auftreten, die den Bogen biegen. Bei konstanter
Streckenlast p muß die Bogenlinie z.B. als quadratische Parabel gekrümmt sein, damit
man einen biegefreien Zustand erhält. Sie wird als Stützlinie bezeichnet. Beim Seil, das
nur Zugkräfte aufnimmt, ist es die Seillinie, die sich unter Eigengewicht z.B. als Ketten–
linie ausbildet.
Bögen und Seile verfügen nur über eine Kraftrichtung. Für jede unterschiedliche Einwirkung
ist daher eine andere Bogen– bzw. Seilform erforderlich, um einen biegefreien Zustand
zu erhalten. Bei Schalen ergeben sich wegen der Flächenwirkung wesentlich
günstigere Verhältnisse. Der biegefreie Gleichgewichtszustand, nämlich der Membranzustand
kann sich entlang von zwei Hauptkraftrichtungen ausbilden. Dieser Zusammenhang
ist im (Bild 5.4) dargestellt.
F

– 5 / 4 –
Bild 5.2 : Innenansicht des Pantheons in Rom, entnommen aus /15/

n 1 links
∆s 1
n 2 unten
F = p 3 ⋅ ∆s 1 ∆s 2
Bild 5.4 : Biegefreier Gleichgewichtszustand bei Schalen
p 3
n 2 oben
∆s 2
– 5 / 5 –
n 1 rechts
n 1 rechts
a) Schalenausschnitt b) Krafteck
n 1 links
n 2 oben
F
n 2 unten
Die resultierende Last, die auf dem Schalenausschnitt (Bild 5.4a) einwirkt, ist im Gleichgewicht
mit den unterschiedlich geneigten Längskräften der beiden Hauptrichtungen,
ohne das Querkräfte auftreten. Die Schließung des Kraftecks (Bild 5.4b) mit zwei Hauptlängskraftpaaren
ist sehr variabel, so daß eine Schale im Gegensatz zum Bogen Stützfläche
für mehr als eine Flächenlast sein kann. Eigengewicht, Schnee und Windeinwirkungen
lassen sich z.B. mit Hilfe einer einzigen geometrischen Form günstig abtragen.
Daraus folgt aber auch, daß eine Last durch unterschiedliche Schalenformen membrangerecht
abgetragen werden kann. Eine optimale Schalenform gibt es daher nicht.
Einzige Voraussetzung für das günstige Tragverhalten ist, daß sich ein biegefreier
Gleichgewichtszustand einstellen kann.
Dies ist der Fall, wenn in der Schale keine geometrischen oder lastbedingten Zwänge
auftreten. Schalenform, Ränder und Lagerung müssen eine konstruktive Einheit bilden
und Einwirkungen dürfen keine sprunghaften Änderungen aufweisen. Kann der Formfindungsprozess
ohne Zwänge nach den erforderlichen physikalischen Bedingungen
des Tragverhaltens gestaltet werden, erhält man ein in jeder Hinsicht optimales Schalenbauwerk.
Auf diesen Ansatz beruht z.B. die Vorgehensweise des Schweizer Bauingenieurs Heinz
Isler /14/. Daß dabei Formen entstehen, die neben den physikalischen auch allen ästhetischen
Anforderungen genügen (Bild 5.1b), ist als Naturgesetz zu deuten, da natürliche
Schalen (Bild 5.1a) durch die Evolution immer beide Bedingungen erfüllen, vgl. /14/.

Schalen zu entwerfen, zu konstruieren und zu bauen ist ein technischer Prozess, der
sich mehr oder weniger an die Bedingungen der konkreten Bauaufgabe orientieren
muß, was zwangsläufig zu einer Beschränkung in der Vielfalt der Schalenformen führt.
Die Mehrzahl der Entwürfe beruht daher auf einer mathematisch und nicht auf einer
physikalisch definierten Schalenform. Mängel, die sich aus dem Unterschied zwischen
vorgegebener und freier Schalenform ergeben, werden durch konstruktive Eingriffe behoben.
Die auf dieser Grundlage konzipierten Schalen erfüllen dann zwar alle formalen
Bedingungen, stellen aber insgesamt keine optimalen Konstruktionen im Hinblick auf
das Tragverhalten dar.
Die Diskrepanz zwischen vorgegebener und freier Schalenform kann besonders bei
Überdachungskonstruktionen sehr groß ausfallen. Willkürlich gewählte mathematische
Formen erfordern i.a. massive Randversteifungen, die zu geometrischen Unverträglichkeiten
zwischen massigen Randträgern und dünner Schale führen. Ein Beispiel für
das Vorgehen mit fester Geometrie ist die Jahrhunderthalle Höchst in Frankfurt a. Main
(Bild 5.5).
a) Ansicht b) Randträger
Bild 5.5 : Jahrhunderthalle Höchst, entnommen aus /14/
– 5 / 6 –

Aus der Ansicht im (Bild 5.5a) ist zu erkennen, daß die Schalenform aus einem polygonförmig
begrenzten Kugelabschnitt besteht. Geschlossene Kugelschalen verfügen über
ein hervorragendes Membran–Tragverhalten. Durch das Aufschneiden nimmt der Widerstand
gegen Ovalisieren aber stark ab. Es würden sich daher reine Biegezustände
mit großen Verformungen einstellen, wenn man keine Randträger gemäß (Bild 5.5b)
anordnet, um den Kugelabschnitt auszusteifen. Im direkten Vergleich zur Schale mit frei
gestalteter Form (Bild 5.1b) stellt die Jahrhunderthalle (Bild 5.5) keine optimale Lösung
dar. Beim Vergleich ist aber zu beachten, daß die Abmessungen der betrachteten Bauwerke
stark differieren. Es bleibt daher offen, ob bei der Jahrhunderthalle eine freie
Formwahl im Hinblick auf das baustatische Verhalten zu deutlich anderen Ergebnissen
führen würde als die feste Formwahl gemäß (Bild 5.5).
Dagegen ist bei Funktionsschalen die Vorgabe fester Geometrien durchaus sinnvoll, da
hier eindeutig die Funktion im Vordergrund des Interesses steht und nicht die Suche
nach einer optimalen und damit ästhetischen Schalenform. Zur Klasse der Funktionsschalen
zählen u.a. auch alle Behälterbauwerke, die sich in der Regel aus einer Vielzahl
von unterschiedlichen Schalenformen zusammensetzen, vgl. z.B. (Bild 1.4).
Wegen des engen Zusammenhangs zwischen Form und Tragverhalten reagieren
Schalen sehr empfindlich auf Veränderungen der Ausgangsgeometrie. Dieser Umstand
erschwert die Konstruktion und den rechnerischen Nachweis erheblich. Vor allem
dann, wenn gleichzeitig die Gefahr des Ausbeulens besteht, da Schalen wegen der
überwiegend auftretenden Druckspannungen verstärkt zum Verlust der Stabilität neigen.
Trotzdem ist der Schalenbau für konstruktive Bauingenieure eine sehr reizvolle
Aufgabe, da er höchste Ansprüche an das baustatische und konstruktive Können stellt.
Dünnwandige Schalen haben von allen Tragwerken den günstigsten Materialeinsatz.
Leider werden sie wegen der hohen Fertigungskosten kaum noch gebaut. Wenn demnach
der Bedarf auch gering ist, so gehört doch eine kurze Einführung in die Schalenstatik
zum unabdingbaren Bestandteil einer Lehrveranstaltung über Flächentragwerke.
Das baustatische Verhalten von Schalen wird durch drei Anteile festgelegt: Durch die
Scheibenwirkung, durch die Plattenwirkung und durch den Einfluß der Schalenform.
Die Scheiben– und Plattenwirkung sind durch die Teile 3 und 4 bekannt. Neu ist der
Einfluß der Schalenform. Es wäre daher sinnvoll, den Einstieg in die Schalentheorie mit
einer allgemeingültigen Betrachtung der Schalengeometrie zu beginnen. Dies erweist
sich im Rahmen einer Einführung aber als zu aufwendig und muß daher einer vertieften
Lehrveranstaltung zur Schalentheorie vorbehalten bleiben. Die Lehrveranstaltung
Statik IV beschränkt sich auf drei Teilaspekte: Im Abschnitt 5.2 auf eine Betrachtung von
technischen Schalenformen, im Abschnitt 5.3 auf die baustatische Berechnung von
Rotationsschalen und im Abschnitt 5.4 auf die Behandlung der Membrantheorie von
allgemeinen Schalen.
– 5 / 7 –

5.2 Technische Schalenformen
5.2.1 Einfluß der Schalenform
Beim Entwurf von Schalen ist die Formgebung als das Hauptproblem anzusehen. Drei
Kriterien sind zu beachten, um optimale Schalenformen zu entwickeln:
1. Die Form darf die Funktion von Schalenbauwerken nicht einschränken.
2. Die Form sollte allen ästhetischen Ansprüchen genügen, die für eine gelungene
Architektur gelten.
3. Die Form ist so zu gestalten, daß sich in Abhängigkeit von der Lagerung maximales
Membrantragverhalten einstellen kann.
Die Chance, alle Kriterien gleichzeitig zu erfüllen, ist wohl nur beim Entwurf von repräsentativen
Schalenbauten gegeben. Bei Nutzbauten steht vor allem die Funktion im Mittelpunkt
des Interesses. Die Forderungen nach einer gelungenen Architektur und
optimalem Tragwerksverhalten treten dagegen zurück. Dies führt dazu, daß freie Schalenformen
in der Regel durch technische Schalenformen ersetzt werden.
Technische Schalenformen beruhen auf festen, mathematisch definierten Geometrievorgaben.
Als bekannte Eingangsgröße sind sie einer statisch–konstruktiven Betrachtung
direkt zugänglich /16/, /17/. Freie Formen sind dagegen zu Beginn der Entwurfsbearbeitung
noch unbekannt. Da sie im Rahmen des Prozesses erst zu ermitteln sind,
bedarf es zusätzliche Kriterien, um sie zu finden. Dazu sind entweder experimentelle
Untersuchungen erforderlich, vgl. /14/, oder man muß spezielle Algorithmen der Tragwerksoptimierung
einschalten, um ans Ziel zu gelangen. In beiden Fällen also eine sehr
aufwendige Angelegenheit, die daher nur in Sonderfällen zur Anwendung kommt.
Den qualitativen Einfluß der Form auf das Tragverhalten von Schalen kann man durch
die charakteristische Flächenkrümmung
K �
1
R 1 ⋅ R 2
– 5 / 8 –
(5.1)
abschätzen. Gl. (5.1) wird nach dem Begründer der Differentialgeometrie der Flächen,
dem Mathematiker F.K. Gauß, als Gauß’sches Krümmungsmaß bezeichnet. Es ist im
(Bild 5.6) veranschaulicht.

R 1
M 2
M 1
R 2
a) K > 0 b) K < 0 c) K = 0
M 1
M 2
Bild 5.6 : Charakteristische Flächenkrümmung
– 5 / 9 –
R 1
R 2
R 2
M 2
R 1 → ∞
Drei Fälle sind zu unterscheiden, die das Tragverhalten von Schalen sehr unterschiedlich
beeinflussen.
1. Im (Bild 5.6a) treten die Hauptkrümmungsradien R 1 und R 2 der Fläche auf einer
Seite der Fläche auf, so daß eine elliptisch geformte Fläche mit positivem Krümmungsmaß
vorliegt. Flächen mit diesen Eigenschaften lassen sich nicht ab–
wickeln. Eine Gestaltungsänderung ohne Dehnung der Fläche ist nicht möglich.
Doppelt gekrümmte Schalen mit positiver Gauß’scher Krümmung K > 0 sind daher
sehr steif und tragen Lasten vorrangig über Membranwirkung ab.
2. Im (Bild 5.6b) treten die Hauptkrümmungsradien R 1 und R 2 der Fläche auf verschiedenen
Seiten der Fläche auf, so daß eine hyperbolisch geformte Fläche mit
negativem Krümmungsmaß vorliegt. Sie enthält schiefwinklig zu den Hauptkrümmungsrichtungen
gerade Erzeugende, die sich ohne Dehnungswiderstand biegen
lassen. Eine Gestaltungsänderung der Fläche kann daher auch durch Biegung
begrenzt werden. Doppelt gekrümmte Schalen mit negativer Gauß’scher
Krümmung K < 0 sind weniger steif als elliptische Flächen. Sie tragen Lasten sowohl
durch Biegung als auch durch Dehnung ab.
3. Im (Bild 5.6c) ist ein Hauptkrümmungsradius der Fläche, hier R 1 , unendlich groß,
da die Schale entlang der betrachteten Hauptrichtung gerade verläuft. Dann ist die
Krümmung dieser Richtung Null und damit auch die Gauß’sche Krümmung der
Fläche. Es gilt K = 0. Die Fläche ist parabolisch geformt und läßt sich ohne Widerstand
abwickeln. Eine Gestaltungsänderung ist nur durch die Biegesteifigkeit des
Schalenquerschnitts zu begrenzen. Es sind also Aussteifungselemente oder spezielle
Lagerelemente erforderlich, um die Gestalt der Schalenform aufrecht zu erhalten.
Parabolisch gekrümmte Schalen tragen Lasten durch Dehnung und Biegung
ab.

5.2.2 Klassifikation von technischen Schalenformen
Zur Klassifikation von Schalenformen erweist es sich als zweckmäßig, eine Einteilung
nach der geometrischen Erzeugungsvorschrift vorzunehmen. Aus der Vielfalt mög–
licher Varianten sind für technische Anwendungen vorrangig Rotations–, Translations–
und Regelflächen von Interesse.
Rotationsflächen sind im (Bild 5.7) dargestellt. Sie entstehen durch Drehung einer ebenen
Meridianlinie um eine Rotationsachse (Bild 5.7a). Die aktuelle Stellung einer Meridianlinie
ist durch die Winkelkoordinate Θ 1 bekannt. Veränderungen innerhalb der Linie
werden durch die Koordinate Θ 2 erfaßt. Sie ist entweder als Länge in Richtung der
Rotationsachse oder als Winkelmaß in der Meridianebene anzugeben, vgl. (Bild 5.7a).
Spezielle Rotationsflächen sind im (Bild 5.7b) dargestellt. Ist die Meridianlinie eine
vertikale Gerade, erhält man einen Zylinder (Bild 5.7b 1). Ist die Gerade dagegen
geneigt, ergibt sich ein Kegel (Bild 5.7b 2). Eine Kugel entsteht, wenn die Vorgabe
der Meridianlinie als zentrischer Kreis erfolgt (Bild 5.7b 3). Ist sie dagegen ein ex–
zentrischer Kreis, erhält man einen Torus (Bild 5.7b 4). Paraboloide (Bild 5.7b 5) oder
Hyperboloide (Bild 5.7b 6) ergeben sich, wenn man als Meridianlinie eine Parabel
oder eine Hyperbel vorgibt.
Translationsflächen sind im (Bild 5.8) dargestellt. Sie sind ebenfalls sehr einfach zu
erzeugen. Dazu ist lediglich eine Erzeugende parallel entlang von zwei gleichen Leit–
linie zu verschieben (Bild 5.8a). Die körperfesten Koordinaten sind beliebig einzuführen.
Θ 1 kann z.B. mit der Erzeugenden zusammenfallen und Θ 2 mit der Leitlinie. Die An–
bindung an die ortsfesten Koordinaten erfolgt durch die Parameterdarstellung des
Ortsvektors, vgl. (Bild 5.8a). Spezielle Regelflächen sind im (Bild 5.8b) dargestellt.
Erzeugende und Leitlinie sind analytisch oder numerisch definierte Raumlinien.
Sie können gleich– oder gegensinnig gekrümmt sein. Die Anzahl unterschiedlicher
Formen ist daher sehr viel größer als bei Rotationsflächen. Beispielhaft sind eine Tonne
im (Bild 5.8b 1) und eine Kugelkappe im (Bild 5.8b 2) dargestellt. Die Tonnenfläche
entsteht, wenn man eine Kreislinie als Erzeugende verwendet und sie entlang einer
geraden Leitlinie verschiebt. Bei der Fläche der Kugelkappe ist die Leitlinie ebenfalls
eine Kreislinie.
Regelflächen sind im (Bild 5.9) dargestellt. Sie entstehen, wenn man eine gerade Erzeugende
entlang von zwei beliebigen Leitlinien führt. Sind die Leitlinien und die Er–
zeugende jeweils windschiefe Gerade, ergeben sich als Flächen parabolische Hyperboloide
(Bild 5.9a). Ist die 1–te Leitlinie dagegen eine Gerade oder Kreis und die 2–te
ein Kreis, so erhält man Konoidflächen (Bild 5.9b).
– 5 / 10 –

Rotations–
achse
X 1
(X 1 , X 2 , X 3 )
(Θ1 , Θ2 ) :
Θ 1
Θ 2
Θ 1
r :
: Ortsfeste
Koordinaten
:
:
X 3 = Θ 2
Körperfeste
Flächenkoordinaten
Winkel in der
Breitenkreisebene
Länge in Richtung
der Rotationsachse
oder Winkel in der
Meridianebene
r : Ortsvektor
Radius im
Breitenkreis
a) Definition b) Spezielle Rotationsflächen
Bild 5.7 : Rotationsflächen
r
r
Θ 2
Meridianlinie
Θ 1 = konstant
Breitenkreislinie
Θ 2 = konstant
X 2
b 1) Zylinder b 2) Kegel
b 3) Kugel b 4) Torus
b 5) Paraboloid b 6) Hyperboloid
– 5 / 11 –

(X 1 , X 2 , X 3 )
(Θ1 , Θ2 ) :
a) Definition
X 3
X 1
: Ortsfeste
Koordinaten
Körperfeste
Flächenkoordinaten
r : Ortsvektor
X 2
Θ 2
Bild 5.8 : Translationsflächen
r
E 1
Θ 1
Leitlinie
b 1) Tonne
b 2) Kugelkappe
b) Spezielle Translationsflächen
– 5 / 12 –
E 2 � E 1
Erzeugende
Zwei gleiche
Gerade als Leitlinie
Kreis als
Erzeugende
Zwei gleiche
Kreise als Leitlinie
Kreis als
Erzeugende

a) Hyperbolisches Paraboloid
1–te Leitlinie: Gerade oder
Kreis
b) Konoid
X 3
X 3
X 2
X 1
X 1
X 2
Bild 5.9 : Regelflächen
1–te Leitlinie: Gerade
r
– 5 / 13 –
r
Θ 1
Θ 2
2–te Leitlinie: Gerade
Θ 2
Θ 1
Erzeugende: Gerade
2–te Leitlinie: Kreis
Grundriß:
Rechteck
oder
Trapez
Grundriß:
Rechteck
Erzeugende: Gerade

Die mathematische Beschreibung von Regelflächen erfolgt wiederum durch eine
Parameterdarstellung, die sich wie bei Translationsflächen in der Regel auf einen
rechteckigen Grundriß bezieht, vgl. (Bilder 5.8b und 5.9a). Bei Regelflächen kann der
Grundriß aber auch trapezförmig begrenzt sein, vgl. (Bild 5.9b).
Technische Schalenformen lassen sich oft auf geometrisch unterschiedlichen Wegen
erzeugen. So kann man z.B. eine Zylinderfläche, die im (Bild 5.7b 1) bereits als Rota–
tionsfläche definiert war, auch als spezielle Translationsfläche erzeugen, indem man als
Erzeugende einen zentrischen Vollkreis entlang von geraden Leitlinien verschiebt, die
mit der Rotationsachse zusammenfallen.
5.2.3 Anwendungen im konstruktiven Ingenieurbau
Im konstruktiven Ingenieurbau ist es üblich, zwischen Behälterschalen, Schalen zur
Überdachung von Grundrissen und reinen Funktionsschalen zu unterscheiden. In den
(Bildern 5.10 bis 5.13) sind typische Beispiele aus diesen Bereichen dargestellt.
Behälterschalen (Bild 5.10) werden am häufigsten gebaut, vgl. auch (Bild 1.4).
a) Faulschlammbehälter b) Kugelgasbehälter
Bild 5.10 : Behälterschalen
– 5 / 14 –

(Bild 5.10a) zeigt einen 45 m hohen Faulturm von eiförmiger Schalenform aus vor–
gespanntem Stahlbeton, der das Kernstück einer biologischen Kläranlage bildet.
(Bild 5.10b) zeigt einen Hochdruck–Kugelgasbehälter von 40 m Durchmesser aus
Stahl, der zur Speicherung von hochverdichtetem Erdgas dient.
Im (Bild 5.11) sind Hallendächer dargestellt. (Bild 5.11a) zeigt ein Faltwerk, das mit zunehmender
Faltenanzahl in eine Tonnenschale übergeht. Sheddächer (Bild 5.11b) entstehen,
wenn man Faltwerke, Tonnen oder Konoide mit Lichtbändern versieht und aneinander
reiht. Bei Faltwerken und Tonnen mit K = 0 dominiert die Spannweite in
Richtung der Geraden. Die Spannweite in Richtung der Schalenkrümmung fällt dagegen
deutlich kleiner aus, vgl. (Bilder 5.11a). Sie kommen vor allem dann zur Anwendung,
wenn es darum geht, Industriehallen zu überdachen. Dies gilt auch für Shed–
dächer gemäß (Bild 5.11b).
Bei quadratischen oder fast quadratischen Grundrissen sind dagegen doppelt
gekrümmte Schalen von Vorteil. Im (Bild 5.11c) ist ein Kappendach mit K > 0 und im
(Bild 5.11d) ein Hypardach mit K < 0 dargestellt. Sie kommen vielfach zur Anwendung,
wenn es darum geht, repräsentative Bauwerke zu überdachen. Das im (Bild 5.11d)
dargestellte, durch Randbalken ausgesteifte hyperbolische Paraboloid ist das große
Dach der wieder aufgebauten Berliner Kongreßhalle, das frei über dem Auditorium
schwebt /18/.
a) Faltwerk– bzw. Tonnendach, aus /17/ b) Sheddach, aus /17/
c) Kappendach, aus /17/
Bild 5.11 : Hallendächer
– 5 / 15 –
d) Hypardach, aus /18/

Als Material zum Bau von Dachschalen bietet sich in der Regel Stahlbeton an ohne und
mit Vorspannung /17/. Eine interessante technische Neuentwicklung stellen aber auch
Netzschalen (Bild 5.12) dar, die zur Klasse der Glaskuppeln gehören /19/. Der tragende
Teil besteht aus einlagigen Gitterrosten mit viereckigen Maschen aus Flachstahlstäben
mit drehbaren Knoten und vorgespannten Diagonalseilen. Die Formgebung ist beliebig
und daher sehr variabel.
Im (Bild 5.12a) ist eine einzelne Kugelkuppel dargestellt und (Bild 5.12b) zeigt eine Kombination
aus zwei, durch eine Zwischenform verbundenen Kugelkuppeln, die durch eine
vertikale Frontfläche begrenzt werden. Die Abwicklung im Grundriß ergibt jeweils Quadratmaschen,
die sich durch rechte Winkel und gleichlange Maschenstäbe auszeichnen,
was die Fertigung der Schalen sehr vereinfacht. Lediglich im Randbereich sind
Stablängen durch Abschneiden anzupassen. Die Viereckmaschen werden einzeln verglast.
Dies gelingt in der Mehrheit der Fälle sogar mit ebenen Glasscheiben, da die einzelnen
Maschen entweder keine oder nur sehr geringe Verwindung aufweisen.
a) Kugelkuppel
b) Kombination aus unterschiedlichen Flächen (ohne Diagonalstäbe)
Bild 5.12 : Verglaste Netzschalen
– 5 / 16 –

Netzschalen (Bild 5.12) sind echte Schalentragwerke. Trotzdem können sie wegen der
Gitterroststruktur als räumliche Stabtragwerke berechnet werden, wodurch sich der
rechnerische Nachweis erheblich vereinfacht, vgl. Teil 6.
Dies trifft für den Kühlturm im (Bild 5.13) nicht mehr zu, der zur Klasse der Funktionsschalen
gehört. Die Gesamtkonstruktion besteht aus einem Rotationshyperboloid, der
auf einem Stützenfachwerk auflagert. Die Höhe kann bis 180. m betragen, der Durchmesser
am Stützenfachwerk bis zu 100. m. Wegen des hyperbolischen Flächentyps
gilt K < 0. In der Regel stellt die Membranlösung keine geeignete Näherung dar, um den
Einfluß der Einwirkungen zu erfassen. Für den gesamten Schalenbereich ist jeweils der
vollständige Satz der Schalenbiegegleichungen zu lösen, um zulässige Ergebnisse zu
erhalten, was einen erheblichen rechnerischen Aufwand erfordert.
+ 117 m
+ 90 m
+ 5.75 m
± 0.
Bild 5.13 : Funktionsschale Kühlturm
∅ 65 m
Rotations–
achse
∅ 50 m
∅ 90 m
– 5 / 17 –
Oberer Rand, t = 0,50 m
Taille, t = 0.35 m
Rotations–
hyperboloid
Unterer Rand, t = 0.75 m
Stützenfachwerk

5.3 Zur baustatischen Berechnung von Rotationsschalen
5.3.1 Allgemeines
Die Ermittlung der Weg– und Kraftzustände von Schalentragwerken gestaltet sich
äußerst schwierig. Analytisch geschlossene Vorgehensweisen sind nur für stark vereinfachte
Problemstellungen bekannt. Erst durch die konsequente Anwendung der FEM
gelingt es, Schalen so zu berechnen, wie es die geplante Konstruktion erfordert, vgl.
z.B. Anwendungsbeispiel 1.5.3, Teil 1.
Die DGL der Scheiben– und Plattentheorie im Teil 3 und 4 erfassen lediglich die Betragsänderungen
von statischen Größen in ortsfesten, also unveränderlichen Koordinatensystemen.
Auf den gekrümmten Flächen von Schalen sind zusätzlich auch noch
die Richtungsänderungen von statischen Größen in nun körperfesten, also veränder–
lichen Koordinatensystemen zu berücksichtigen. Dies führt zu einer Kopplung der
Scheiben– und Plattenwirkung, so daß sich der Aufwand zur Formulierung und Lösung
der baustatischen Aufgabe Schalenberechnung im Vergleich zur reinen Scheiben–
oder Plattenberechnung deutlich erhöht.
Baustatische Berechnungsmethoden beruhen auf analytischen Vorgehensweisen. Sie
sind i.a. durch eine Vielzahl von Vereinfachungen gekennzeichnet, die lediglich für spezielle
Konstruktionen gelten. Ein technisch wichtiger Anwendungsfall sind z.B. Behälter
von rotationssymmetrischer Schalenform unter Füllungsdruck, die sich mit dem KGV
oder dem WGV berechnen lassen.
Grundlage der Berechnung von Rotationsschalen (Bild 5.14) ist die Membrantheorie.
Sie beschreibt die Gleichgewichtsbedingungen der Schalentheorie als reinen Dehnungszustand
an einem SGS, das aus dem wirklichen System durch die Änderung der
Lagerungsbedingungen entsteht. Die Lagerung ist im Hinblick auf die Biegung in der
Weise zu modifizieren, daß ein denkbarer Biegezustand ersatzlos entfällt. Bei der Konstruktion
der Rotationsschale im (Bild 5.14a) ist speziell die feste und unverschiebliche
Einspannung der Schalenwand in die Fundamentplatte (Bild 5.14b) durch eine gelenkige
und horizontal verschiebliche Lagerung (Bild 5.14c) zu ersetzen, um einen biege–
freien Beanspruchungszustand zu erhalten. Die Annahme einer festen Einspannung im
statischen System (Bild 5.14b) ist allerdings nur zulässig, wenn ein sehr steifer Baugrund
vorliegt und die Dicke der Fundamentplatte deutlich größer ausfällt als die Dicke
der Schalenwand. Die Umwandlung von statischen Systemen (z.B. Bild 5.14b) in SGS
(z.B. Bild 5.14c) ist immer möglich, wenn auch nicht immer so einfach wie bei der Rota–
tionsschale im (Bild 5.14). Wegen der Rotationssymmetrie von Geometrie und Einwirkungen
verschwinden die horizontalen Verschiebungen in der Rotationsachse, so daß
im vorliegenden Fall ein eindeutig gefesseltes SGS vorliegt. Dies ist bei der Betrachtung
von (Bild 5.14c) zu beachten, das beim ersten Anblick wie ein kinematisches
System aussieht.
– 5 / 18 –

Schalenwand Füllung γ
ÎÎÎÎÎÎÎÎÎÎÎÎÎÎ
ÎÎÎÎÎÎÎÎÎÎÎÎÎÎ
ÎÎÎÎÎÎÎÎÎÎÎÎÎÎ
ÎÎÎÎÎÎÎÎÎÎÎÎÎÎ
Fundamentplatte
ÎÎÎÎÎÎÎÎÎÎÎÎÎÎ
Bild 5.14 : Rotationsschale
Rotationsachse (RA)
Baugrund
– 5 / 19 –
RA
Feste Ein–
spannung
Füllungsdruck
p 3
RA
Gelenkige
Lagerung
a) Konstruktion b) Statisches System c) SGS
Biegung entsteht demnach nur durch Zwängungen zwischen Schalenwand und Fundamentplatte.
Am SGS ist also die Verträglichkeit zu erfüllen, um diesen Störungszustand
zu ermitteln. Die Berechnung ist nach den Regeln des KGV durchzuführen. Es sind
die Einwirkungs– und Einheitskraftzustände am SGS zu definieren, aus dem Gelenkschluß
die statischen Unbestimmten zu berechnen und durch Superposition die Bemessungsgrößen
zu ermitteln.
Natürlich läßt sich auch ein vergleichbares WGV ableiten. Das dazu erforderliche GGS
ist aber erheblich komplizierter als das besonders einfache Membransystem des SGS,
da es in der Regel partikuläre Biegelösungen der Schalentheorie voraussetzt, die nur
im beschränkten Umfang vorliegen. In der klassischen Baustatik der Schalen wird das
WGV daher kaum angewandt. Standardverfahren ist die Vorgehensweise mit Kraftzuständen.
Die Methodik des KGV gilt auch für zusammengesetzte Rotationsschalen
und ist z.B. im Markus /8/ sehr ausführlich dargestellt.
5.3.2 Membranlösung
Die Rotationsschale im (Bild 5.14) besteht lediglich aus einem Kreiszylinder, wenn man
die Fundamentplatte und den Baugrund im Rahmen der Schalenberechnung vernachlässigt.
Das Berechnungssystem der Membrantheorie ist im (Bild 5.15) dargestellt.
p 3

Freier Rand
Kreiszylinder Füllung γ
ϕ 2
Θ 2
u 3
R
RA
n 12 = n 21
Θ
a) SGS b) Füllungsdruck
1 = ω
Membranlagerung
n 22
Bild 5.15 : Berechnungssystem der Membrantheorie
Die körperfesten Koordinaten Θ 1 und Θ 2 beschreiben die Ring– und Meridianrichtung
der Schale. Θ 2 stimmt mit der Bogenlänge des Meridians überein. Θ 1 ist dagegen keine
Bogenlänge, sondern ein Winkelmaß der Ringrichtung. Es ist daher eine Umrechnung
erforderlich, um Bemessungsgrößen zu erhalten, die sich grundsätzlich auf Bogenlängen
beziehen. Die Schalennormale ist als Senkrechte der Tangentialfläche definiert, die
zu jedem Punkt von Θ 1 und Θ 2 gehört.
Am SGS (Bild 5.15a) sind die Kraft– und Wegzustände zu ermitteln, die sich durch den
Füllungsdruck (Bild 5.15b) nach der Membrantheorie ergeben. Wegen der Rotationssymmetrie
des Füllungsdrucks
p 3 � � �H � � 2�, (5.1)
der in Richtung der Schalennormale wirkt, gibt es keine Schiefstellung in der Schalen–
fläche, so daß die Schubkräfte n 12 = n 21 entfallen. Das Gleichgewicht ist in Ring–, Meridian–
und Normalenrichtung zu erfüllen.
Ringrichtung
Meridianrichtung
Normalenrichtung
:
:
:
n 11 ,1 = 0.
n 22 ,2 = 0.
� 1
R n11 � p 3
� 0.
– 5 / 20 –
n 11
Θ 2
p 3
u 3
H
(5.2.1)
(5.2.2)
(5.2.3)
In Ring– und Meridianrichtung wirken keine Lasten. Die Längskräfte n 11 GL. (5.2.1) und
n 22 (Gl. 5.2.2) ändern sich daher nicht. Der obere Rand ist ein freier Rand, so daß dort
keine Längskräfte auftreten können. Die Meridianlängskraft n 22 muß daher Null werden.

Das Gleichgewicht in Normalenrichtung Gl. (5.2.3) kann im Rahmen der statisch bestimmten
Membrantheorie mit dem Schnittprinzip aufgestellt werden. Im Ringschnitt
(Bild 5.16) ist der halbe Zylinder dargestellt.
n 11
n 11
R
R
�
90°
Bild 5.16 : Schnittprinzip zur Bestimmung von n 11
p 3
p 3
p 3
H
�
p 3
H
�
p 3
V
p 3
V
– 5 / 21 –
Innendruck:
Vertikale Komponente:
Horizontale Komponente:
p 3
p 3
V � cos � p3
p 3
H � sin � p3
Die vertikalen Komponenten des Innendrucks heben sich gegenseitig auf. Für die horizontale
Komponente gilt:
2n11 � � 180o
p 3
Hds � p3R� �
0
Daraus folgt Gl. (5.2.3) oder die Faßformel
0
sin � d� � p 3 R [� cos �] �
0 � 2p3 R.
n 11 � p 3 R . (5.3)
Stellt man z.B. gedanklich eine Scheibe in den Zylinder, so erhält man im Ringschnitt
das Gleichgewichtssystem
p 3
Scheibe
p 3
Scheibe
und daraus durch einen speziellen Schnitt durch die Scheibe unmittelbar Gl. (5.3), ohne
integrieren zu müssen.
n 11
n 11
p 3
R
R

Die Ringkraft in einer zylindrischen Schalenwand ergibt sich aus dem Produkt Flächenlast
mal Zylinderradius, wenn eine statisch bestimmte Membranlagerung vorliegt,
die eine freie Verschiebung in Richtung der Einwirkung ermöglicht, vgl. (Bild 5.15a).
Speziell für den Füllungsdruck Gl. (5.1) gilt
n 11 � R� �H � � 2� . (5.4)
Mit bekanntem Kraftzustand kann man den Wegzustand am SGS ebenfalls ermitteln.
Von Interesse ist lediglich die Ringrichtung, da nur hier Kräfte auftreten. Es gilt die Verträglichkeitsaussage
der Ringdehnung
� K 11 � �M 11
. (5.5)
Die formale Darstellung von Gl. (5.5) ist bereits aus der Scheibentheorie bekannt, vgl.
Teil 3. Der kinematische Anteil (Index K) ist bei Rotationsschalen als normierte Differenz
der Bogenlängen des verformten und des unverformten Ringquerschnitts definiert. Die
Bogenlängen sind im (Bild 5.17) dargestellt.
Bild 5.17 : Bogenlänge im Ringquerschnitt
R
u 3
verformte Bogenlänge
unverformte Bogenlänge s
Durch den Füllungsdruck verschiebt sich die Schalenwand gleichmäßig um das Maß
u 3 nach außen. Die Bogenlänge der verformten Schalenwand beträgt
s ~ � 2 �R � u 3 � � (5.6.1)
und die Bogenlänge der unverformten Schalenwand
s � 2R� . (5.6.2)
Mit Gl. (5.6.1) als Normierungslänge errechnet sich die Ringdehnung zu
� K 11 � s~ � s
s
. (5.7)
– 5 / 22 –
s ~

Gl. (5.6) in Gl. (5.7) eingesetzt, ergibt
� K 11 � u 3
R
. (5.8)
Die kinematische Ringdehnung Gl. (5.8) muß mit der Ringdehnung übereinstimmen,
die das verwendete Material (Index M) zuläßt. Für elastisches Material gilt wie bei
Scheiben die Beziehung
� M 11
� 1
Et �n 11 � � n 22� . (5.9)
Gl. (5.8 und 5.9) unter Beachtung von Gl. (5.4) und n 22 = 0 in Gl. (5.5) eingesetzt ergibt
u 3
R
n11
�
Et � R� �H � �2� Et
. (5.10)
Die Auflösung von Gl. (5.10) nach u3 liefert dann die Bestimmungsgleichung der gesuchten
Weggröße. Es gilt
u3 � R2� �H � �2� . (5.11)
Et
Mit Gl. (5.11) ist auch die Meridianverdrehung bekannt. Es gilt
��u3,2 �� � u3 � �2 � R2� ϕ2
. (5.12)
Et
Die Membranlösung ist im (Bild 5.18) dargestellt. Veränderungen ergeben sich nur in
Richtung der Koordinate Θ 2 des Meridians. In Richtung der Koordinate Θ 1 des Breitenkreises
sind die Größen dagegen wegen der Rotationssymmetrie von Geometrie und
Einwirkung konstant. (Bild 5.18a) zeigt den Verlauf der Ringkraft Gl. (5.4), (Bild 5.18b)
den Verlauf der Durchbiegung Gl. (5.11) und (Bild 5.18c) den Verlauf der Verdrehung
Gl. (5.12).
n 11
Θ 2
Bild 5.18 : Membranlösung
u 3
+ +
+
�RH
�R 2 H
Et
– 5 / 23 –
ϕ2
�R 2
Et
a) Ringkraft b) Durchbiegung c) Verdrehung
Oberer Rand
Unterer Rand

5.3.3 Biegelösung
Aus (Bild 5.18b und c) ist zu entnehmen, daß sich bei der Membranlösung am unteren
Rand (Koordinate Θ 2 = 0) eine Durchbiegung und eine Verdrehung einstellt, die beim
wirklichen System nicht auftreten können, da hier eine feste Einspannung vorliegt, vgl.
(Bild 5.14b). Es sind also entlang des Breitenkreises arbeitskonforme Kraftzustände am
Ort der Störung anzubringen, um den Einspannzustand wieder herzustellen. Zur Rücknahme
der Durchbiegung u 3 (Θ 2 = 0) ist eine umlaufende Querkraft Q und zur Rücknahme
der Verdrehung ϕ 2 (Θ 2 =0) ein umlaufendes Moment M anzubringen. Beide
führen zu einer Biegebeanspruchung der Schalenwand. Es ist also neben der Membrantheorie
auch noch eine Biegetheorie abzuleiten, um diesen Zustand zu erfassen.
Das Berechnungssystem der Biegetheorie ist im (Bild 5.19) dargestellt. Es stimmt mit
dem SGS der Membrantheorie überein. (Bild 5.19a) zeigt den Einwirkungszustand und
(Bild 5.19b) die dadurch auftretenden Zustandsgrößen.
H
Θ 2
Bild 5.19 : Berechnungssystem der Biegetheorie
R
t
Q
Θ1 = ω
M
Membranlagerung
– 5 / 24 –
Θ 2 , u 2
u 3
n 22
m22 m11 a) SGS und Einwirkung b) Zustandsgrößen
Die Weggrößen u 1 und ϕ 1 sowie die Kraftgrößen n 12 = n 21 , m 12 = m 21 und q 13
entfallen, da es sich bei den Randgrößen Q und M um rotationssymmetrische Ein–
wirkungen handelt. Wegen des freien Randes am oberen Ende der Rotationsschale
(Koordinate Θ 2 = H) tritt auch im Rahmen der Biegetheorie keine n 22 –Kraft entlang
des Meridians auf. Eine einwirkungsbedingte Krümmung in Ringrichtung kann sich
ebenfalls nicht ausbilden. Es gilt � K 11 � 0. Das Ringmoment m11 ist daher durch
die Verträglichkeitsaussage
� K 11 � �M 11 � B* �m 11 � � m 22� � 0 � m 11 � � m 22 (5.13)
als ν–facher Wert des Meridianmoments m 22 bekannt und spielt für die weitere Betrachtung
keine Rolle. Gl. (5.13) ist bereits aus der Plattentheorie bekannt, vgl. Teil 4.
Dort gilt sie z.B. für Plattenstreifen unter Gleichlast, deren Krümmung in einer Richtung
ebenfalls verschwindet.
q 23
ϕ 2
n 11
Θ 1

Von den Gleichgewichtsbedingungen Gl. (5.2) ist nur Gl. (5.2.3) von Interesse, die das
Kräftegleichgewicht in Normalenrichtung der Schalenwand beschreibt. Sie gilt auch für
die Biegetheorie, wenn man den Einwirkungsterm p3 äquivalent durch die erste Ableitung
q23 ,2 der Querkraft q23 ersetzt und diesen Term wiederum durch die zweite Ableitung
m22 ,22 des Meridianmoments m22 ausdrückt; Zusammenhänge, die sich wegen
des geraden Verlaufs der Meridianrichtung und der Rotationssymmetrie ebenfalls unmittelbar
aus der Plattentheorie ergeben. Es gilt
� 1
R n11 � m22 ,22 � 0. (5.14)
Die Bestimmungsgleichungen für die Längskräfte sind durch das Auflösen der Verträglichkeitsaussagen
� K 11 � �M 11 und �K 22 � �M 22 nach n11 und n 22 zu ermitteln. Die
formale Darstellung ist wiederum aus der Scheibentheorie bekannt, vgl. Teil 3. Für Rotationsschalen
gilt speziell
und
� K 11
� K 22
n 11 � D � 1
R u 3 � � u 2,2� (5.14.1)
� K 22
� K 11
n 22 � D �u 2,2 � � 1
R u 3� � 0. (5.14.2)
Gl. (5.14.2) nach u 2,2 aufgelöst und in Gl. (5.14.1) eingesetzt, ergibt für die Ringkraft
den Ausdruck
n 11 � D
R �1 � � 2� u 3 . (5.15)
Die Bestimmungsgleichungen für die Biegemomente sind durch das Auflösen der Verträglichkeitsaussagen
� K 11 � �M 11 und �K 22 � �M 22 nach m11 und m 22 zu ermitteln,
die sich, wie bereits angemerkt, unmittelbar aus der Plattentheorie ergeben. Die Berechnungsgleichung
für m 11 ist von untergeordneter Bedeutung und entfällt. Mit
� K 11 � 0 verbleibt für m22 der Ausdruck
� K 22
m 22 � B �� u 3,22 � . (5.16)
Die Ringkraft Gl. (5.15) und das Meridianmoment Gl. (5.16) hängen nur von der Durchbiegung
u 3 ab. Das Kräftegleichgewicht in Richtung der Schalennormale Gl. (5.14)
kann daher allein durch die Weggröße u 3 ausgedrückt werden. Mit der Annahme einer
konstanten Plattensteifigkeit B erhält man zunächst die DGL
� D
R 2 �1 � � 2� u 3 � Bu 3,2222 � 0.
– 5 / 25 –

Mit dem Verhältnis von Scheiben– und Plattensteifigkeit bzw. der Dehn– und Biege–
steifigkeit der Schalenwand
D
B �
folgt die Form
Et
�1�� 2�
Et 3
12 �1�� 2�
� 12
t 2
u 3,2222 � 12 �1 � � 2�
R 2 t 2
u 3 � 0
oder mit der Abkürzung
3 �1 � �
� � H
2�
R2 t2 4� (5.17)
endgültig
u 3,2222 � 4 � �
H �4
u 3 � 0. (5.18)
Die DGL (5.18) beschreibt die Biegelösung von geschlossenen Kreiszylinderscha–
len, wenn rotationssymmetrische Randgrößen auf die Schale einwirken. Die Struktur
von Gl. (5.18) stimmt vollständig mit der DGL von gebetteten Biegebalken überein, vgl.
z.B. /12/. Die Abkürzung Gl. (5.17) kann daher als Abklingfaktor der Lösung
�
u3 � e��H��2�C1 cos�� – 5 / 26 –
�� 2�
H ��2 � C2 sin�� H
�
� e��H�� 2�C3 cos�� H �� 2 � C4 sin�� H �� 2� gedeutet werden, die zu einem elastisch gebetteten Balken mit der Bettungszahl
K � Et�1 � � 2�
R 2
(5.19)
(5.20)
und der Länge s = H gehört. Gl. (5.20) folgt aus dem Vergleich der Abklingfaktoren
von Schale und Balken, die mit H = s gleiche Höhen– bzw. Längenabmessungen
aufweisen. Beide Systeme sind im (Bild 5.20) dargestellt. Im (Bild 5.20a) sind die Zusammenhänge
bei der Schale und im (Bild 5.20b) beim Balken angegeben.

System
DGL
Abkling–
faktor
Rotations–
achse
u 3
Θ 2
Θ 1 = ω
R
u 3,2222 � 4 � �
H �4
u 3 � 0
� � H
t
E, ν
u 3
3 �1 � �2� R2 t2 4� � H
R 3 �1 � �2� 4�
a) Kreiszylinderschale b) Elastisch gebetteter
Balken
Bild 5.20 : Vergleich zwischen Kreiszylinderschale und elastisch gebetteten Balken
– 5 / 27 –
Oberer Rand
Θ 2
Θ 2
�
R
t
H
Unterer Rand
Bettung K der Schale
Linker
Rand
w
s
x x
EI
Rechter
Rand
Bettung K des
Baugrunds
w���� � 4 �� s�4w � 0
� � s
4� K
4EI
Die Biegelösung Gl. (5.19) besteht aus zwei Anteilen (Bild 5.21). Es sind periodische
cos– und sinus–Schwingungen, die von den Schalenrändern Θ2 (Bild 5.21a) bzw.
Θ2 (Bild 5.21b) ausgehen und als Folge der negativen Exponenten der e–Funktion
⋅�R � hän-
abklingen. Die Zahlenwerte der Abklingfaktoren, z.B. �� H � �2 � �2
R �3 1�4
�1 � �2� t�1�2 gen maßgeblich vom Verhältnis �R t� ab, wenn ��2 R� � 1 ist, es sich also nicht um extrem
kurze Schalen handelt. �R t� �� 1 ist dagegen stets erfüllt. Dadurch sind bei praktischen
Problemen in der Regel sehr große Abklingfaktoren zu erwarten, so daß die
Lösungen lediglich in einem schmalen Randbereich auftreten und die Schalen– ränder
sich nicht gegenseitig beeinflussen. Das Verhältnis von zwei, um die Periode T versetzten
Schwingungsamplituden ist z.B. durch
u 3�T
u 3 �
e�� �
H �(�2 �T)
e
� �� ��2 H
� e�� �
H �T � 2 �2� � 0.00187 .

u 3
a) Anpassen der Randbedingungen mit Θ 2 = 0
Rand Θ 2 = 0
Θ 2
Kein Einfluß
c) Schwingungsperiode:
Bild 5.21 : Biegelösung
cos���� 2
H
sin�� H
Θ 2
u 3
b) Anpassen der Randbedingungen mit
e
T
H
T
e
cos�� H
sin�� 2
��
H
� 2
�� �� H
�� 2
� �� ��2 H
Θ 2
�� 2
Θ 2 = 0
– 5 / 28 –
Θ 2
Kein Einfluß
u 3
�� H �T � 2� � T �
2� ⋅ R
3(1 � �2 4� )
Rand Θ 2 = 0
⋅
R
R
�t
R

ekannt, wobei T nach (Bild 5.21a bzw. b) die Länge einer vollen Schwingung in
Θ 2 – bzw. Θ 2 –Richtung angibt, die wegen � t
R � �� 1 nur einen Bruchteil des Schalenradius
R beträgt (Bild 5.21c). Die Anpassung der Lösung Gl. (5.19) an die vorliegenden
Randbedingungen kann daher getrennt für die einzelnen Schalenränder, also in entkoppelter
Form erfolgen. Dazu müssen jeweils zwei Bedingungen pro Schalenrand bekannt
sein, entweder zwei geometrische, zwei statische oder eine geometrische und
eine statische Randbedingung.
Mit dem ersten Anteil der Lösung Gl. (5.19) sind dann auch alle weiteren Zustands–
größen der abklingenden Biegelösung des Θ 2 –Schalenrandes bekannt. Im einzelnen
gilt
und
n 11 � D
R �1 � � 2� u 3 , (5.21.1)
ϕ
2 ��u3,2 , (5.21.2)
m 22 ��Bu 3,22
– 5 / 29 –
(5.21.3)
q 23 ��Bu 3,222 . (5.21.4)
Die Durchführung der Ableitungsvorschrift ergibt
und
� �C1 � C � 2 cos�� H ��2 � �C1 � C � 2 sin�� H
� C2 cos�� ��2�, (5.22.1)
H ��2 � C1 sin�� m ��2� H 22 �
� (5.22.2)
�
�
�
�e�� ��2 H
H 2 �
B2�� �
�e�� ��2 H
H
q23 � B2�� H �3
�
e��H �� 2
�� �C 1 � C 2 � cos� �
H �� 2 � �C 1 � C 2 � sin� �
H �� 2�. (5.22.3)
Für den Θ 2 –Schalenrand ist lediglich Θ 2 mit Θ 2 zu tauschen, um auch dort Lösun–
gen zu erhalten. Durch die Vorgabe der statischen Randbedingungen Q und M für
Θ 2 = 0 können abschließend die Konstanten C 1 und C 2 bestimmt werden, so daß
eine eindeutige Lösung des Randstörungsproblems der Kreiszylinderschale vorliegt.

5.3.4 Beispiel Wasserbehälter
Es sind die maßgeblichen Bemessungsgrößen zur Auslegung eines randvoll gefüllten
Wasserbehälters aus Stahlbeton nach der linear–elastischen Schalentheorie zu er–
mitteln. Das Berechnungssystem ist im (Bild 5.22) dargestellt. Die Geometrie des Behälters
besteht aus einer kreiszylindrischen Schalenform. Die Wanddicke ist konstant
und der Behälterfuß fest in ein umlaufendes Fundament eingespannt. Eine obere Abdeckung
ist nicht vorhanden.
H = 8. m
t = 0.24 m
Ç
Ç
Ç
Ç
Ç
Ç
Ç
Ç
ÉÉÉÉÉ
Ç ÉÉÉÉÉ
Ç ÇÇÇÇÇÇÇÇÇÇÇÇÇÇ
ÉÉÉÉÉ
ÉÉÉÉÉ
9. m
Bild 5.22 : Wasserbehälter, aus /4/
Rotations–
achse
Wasserfüllung (γ)
Wasserdruck
Betonplatte
– 5 / 30 –
R = 9. m
Ç
Ç
Ç
Ç
Ç
Ç
ÉÉÉÉÉ
ÉÉÉÉÉ
Kreiszylinder
E = 3 ⋅ 107 kN/m2 ν = 0.2
Fundament
Der Wasserdruck ist ein rotationssymmetrischer Lastfall, so daß keine antimetrischen
Zustandsgrößen (u 1, ϕ 1, n 12 = n 21 , m 12 = m 21 , q 13 ) auftreten. Von den symmetrischen
Zustandsgrößen sind (u 2, n 22 und m 11 ) von untergeordneter Bedeutung. Die Ver–
drehung ϕ 2 wird lediglich zur Durchführung der Berechnung nach dem KGV benötigt.
Als Bemessungsgrößen zur Dimensionierung der Behälterwand sind also nur die im
(Bild 5.23) dargestellten Zustandsgrößen (u 3, n 11 , m 22 und q 23 ) zu ermitteln.

Θ 1
Θ 2
u 3
= Ringrichtung.
= Meridian– bzw. Längsrichtung.
= Richtung � zur Behälterwand.
Bild 5.23 : Bemessungsgrößen
Die Gesamtlösung der Durchbiegung
u 3 � u 3h � u 3p
setzt sich aus zwei Anteilen zusammen. Die homogene Lösung (Index h) erfaßt die
Randbedingungen des Systems und die partikuläre Lösung (Index p) die Wirkung
des Wasserdrucks. Das Anpassen der Randbedingungen ist ein Randstörungs–
problem. Es ist näherungsweise durch die abklingende Biegelösung Gl. (5.19) und
Gl. (5.22) bekannt. Die partikuläre Lösung kann ebenfalls durch eine Näherung ersetzt
werden. Hierfür bietet sich die Membranlösung Gl. (5.4), Gl. (5.11) und Gl. (5.12) an,
da der Wasserdruck großflächig auf die Wand einwirkt. Sie ist im (Bild 5.24) dargestellt.
H
Rotations–
achse
Θ 2
R
Membranlagerung
Wasser–
druck
– 5 / 31 –
Θ 2
m 22
Bild 5.24 : Partikuläre Lösung = Membrantheorie = 0–Zustand am SGR
p 3
Ring–
kraft
+
n 11
0
u 3
q 23
Durch–
biegung
+
u 30
n 11
+
Θ 1
Ver–
drehung
ϕ 20

Die Anwendung der Membrantheorie setzt voraus, daß Randbedingungen vorliegen,
die eine zwängungsfreie Durchbiegung erlauben. Im SGS (Bild 5.24) ist die Einspannung
der Behälterwand daher durch eine momentenfreie und verschiebliche Lagerung
zu ersetzen, um diese Bedingung zu erfüllen. Aus der Gleichgewichtsbedingung in
Ringrichtung folgt dann die Ringkraft
n 11
0 � Rp3 � R� (H � � 2 )
und aus der zugeordneten Verträglichkeitsbedingung die Durchbiegung
u30 � R n11
0
Et � R2 � (H � �2 )
Et
.
Mit u 30 ist durch ϕ 20 = – u 30,2 auch die Verdrehung im Momentengelenk bekannt.
�
20� R2
Et .
ϕ
Im wirklichen System sind in der Einspannung Θ 2 = 0 die Durchbiegung u 3 und die
Verdrehung ϕ 2 Null. Die partikulären Lösungen u 30 und ϕ 20 müssen daher mit homogenen
Lösungen u 3j und ϕ 2j überlagert werden, um dies zu erreichen. Dazu sind am
SGS (Bild 5.24) der Membrantheorie die j = 1, 2 arbeitskonformen Einheitskraftzustände
X j anzubringen, die Vergleichswerte zur Erfüllung der Lagerbedingungen durch
die Auswertung der Biegelösung zu berechnen und die Verträglichkeitsbedingungen
und
u 3 (� 2 � 0) � u 30 (� 2 � 0) � X 1 ⋅ u 31 (� 2 � 0, X 1 � 1)
� X 2 ⋅ u 32 (� 2 � 0, X 2 � 1) � ! 0
22 (�2 � 0, X2 � 1) � ! 2
0
(�2 � 0) � 20 (�2 ϕ ϕ � 0) � X1 ⋅ 21
� X2 ⋅
(�2 ϕ � 0, X1 � 1)
ϕ
aufzustellen. Der X 1–Zustand ist im (Bild 5.25) und der X 2–Zustand im (Bild 5.26) dargestellt.
Angegeben sind jeweils unter a) das System, unter b) die Bestimmung der
Konstanten und unter c) die Lösung des Biegeproblems für die Einheitszustände.
– 5 / 32 –

a) System
c) Lösung
Θ 2
Membranlagerung
X1 � q23 1 ��2 � 0� � 2B ��
H�3 X2 � m22 1 ��2 � 0� � 2B ��
H�2 b) Bestimmung der Konstanten
u 31 � 1
m 22
1
q 23
1
C 1 �� 1
2B ��
H
�
�
1
e��
�
� �
H
2B ��
H �3 und C 2
���
2
e��H �3
��2 H
Bild 5.25 : X 1–Zustand = Querkraft am SGR
– 5 / 33 –
Rotationsachse
R
�� C 1 � C 2 � � 1.
� C 2 � � 0.
� 0.
X2 = 0.
X1 = 1.
cos� �
H �� 2 ,u 31 �� 2 � 0� �� 1
sin� �
H �� 2 ,
� e�� �
H �� 2�cos� �
H �� 2 � sin� �
H �� 2� .
2B ��
H
� 21 �� 2 � 0� �� 1
2B ��
H
�3 ,
�2 ,

a) System
c) Lösung
Θ 2
Membranlagerung
X1 � q23 2 ��2 � 0� � 2B ��
H�3 X2 � m22 2 ��2 � 0� � 2B ��
H�2 C 2 ��C 1 � 1
b) Bestimmung der Konstanten
u 32 �� 1
m 22
2
q 23
2
2B ��
H
�2 .
2B ��
���
2�cos� e��
�
H
�2
H
Bild 5.26 : X 2–Zustand = Biegemoment am SGR
– 5 / 34 –
Rotationsachse
R
�� C 1 � C 2 � � 0.
� C 2 � � 1.
���2�cos�
� e��
�
H
H ��2 � sin�� H ��2� ,
��2� �
H �� 2 e
� �� ��2 H
X 2 = 1.
X 1 = 0.
H ��2 � sin�� H ��2�, u �� 32 2 � 0� �� 1
sin� �
H �� 2 .
2B ��
H
� 22 �� 2 � 0� �� 1
2B ��
H
�2 ,
� ,

Die explizite Form der Verträglichkeitsbedingungen ist durch
X 1
1
2B ��
H �3
1
2B ��
H �2
– 5 / 35 –
X 2
1
2B ��
H �2
Lastzustand
R 2 �H
Et
gegeben. Die Lösung des algebraischen Gleichungssystems führt für die statisch Un–
und
Lagerbedingung
u 3 (Θ 2 = 0) = 0
ϕ 2 (Θ 2 = 0) = 0
bestimmten auf die Werte:
Damit sind dann auch die gesuchten Bemessungsgrößen bekannt:
und
X 1 �� 2B R2 � ��
H �2
Et
X 2 � 2B R2 � ��
H �
Et
u 3 � u 30 � X 1 ⋅ u 31 � X 2 ⋅ u 32 ,
n 11 � Et
R u 3 ,
(1 � 2�) �� �
(1 � �) �� �
m22 � m22 0 � X1 ⋅ m22
1 � X2 ⋅ m22
2
2� �
(1 � 2�)
�2
H
2�� (1 � �) .
�3
H
Membrantheorie !
mit m22
0
� 0
q23 � q23 0 � X1 ⋅ q23
1 � X2 ⋅ q23
2 mit q23 0 � 0.
1
B ��
H �
R 2 �
Et

Die Auswertung der Superposition führt auf die Ausdrücke
und
u 3 �
� R2
Et ��H � � 2� � He
n 11 � � R��H � � 2� � He
m 22 � �
2� �
H
F 2
F 3
Die Verläufe der Bemessungsgrößen sind im (Bild 5.27) dargestellt.
�
Wasserspiegel
2 (m)
u 3 � �R2
Et F 1
n 11 � �RF 1
F 3
� �� ��2�cos�� H
–8. –6. –4. –2. 0. +2. +4. +6. +8.
Bild 5.27 : Verlauf der Bemessungsgrößen
0.
F 1
� �� ��2�cos�� H
�3�e �� �
H �� 2�(1 � �) cos� �
8.
7.
6.
5.
4.
3.
2.
1.
– 5 / 36 –
H��2 ��1 � 1�
sin��
� H��2�� ,
H��2 ��1 � 1�
sin��
� H��2�� ,
H��2 � � sin�� H��2�� q23 � �
2�� H �2��
�
e��H��2�(1 � 2�) cos�� H��2 � sin�� H��2�� .
F 1
F 2
m 22 � �
2� �
H �3 F 2
q 23 � �
2� �
H �2 F 3
Membrantheorie

In der oberen Hälfte des Behälters stimmt die Verteilungsfunktion F 1 der Durch–
biegung u 3 und der Ringkraft n 11 mit den Ergebnissen der Membranlösung überein.
Biegelösungen treten daher nur in der unteren Hälfte des Behälters auf. Die Ver–
teilungsfunktionen F 2 des Biegemoments m 22 und F 3 der Querkraft q 23 nehmen
am Behälterfuß (Koordinate Θ 2 = 0) ein Maximum an, weil dort die Einspannbe–
dingungen u 3 (Θ 2 = 0) = 0. und ϕ 2 (Θ 2 = 0) = 0. gelten, die den größten Zwang er–
geben. Bei Θ 2 ≈ 1. wechseln sie das Vorzeichen und klingen danach sehr schnell ab,
vgl. (Bild 5.27). Die Ringkraft n 11 verschwindet am Behälterfuß ebenfalls, da in der Einspannung
keine Ringdehnung und somit auch keine Kraft auftreten kann.
Die Lösungen gemäß (Bild 5.27) hätte man auch unmittelbar aus Gl. (5.19) und
Gl. (5.22) durch Anpassen der Konstanten ermitteln können, ohne das KGV anwenden
zu müssen. Die Methodik des KGV ist aber wesentlich anschaulicher als die direkte
Integration der DGL. Darüber hinaus läßt sie sich in einfacher Weise auf beliebige Anwendungsfälle
erweitern (Bild 5.28); z.B. auf Behälter, die Sprünge in der Wanddicke
aufweisen (Bild 5.28a) oder auf Behälter, die sich aus zwei oder mehr Teilschalen zusammensetzen
(Bild 5.28b).
t 2
t 1
a 1) Statisches System
Rotationsachse
a 2) SGS
a) Behälter mit Wanddickensprung
Bild 5.28 : Anwendungsfälle
Füllung γ Füllung γ
m 22 = X 1
q 23 = X 2
m 22 = X 3
q 23 = X 4
– 5 / 37 –
t
Rotationsachse
b 1) Statisches System b 2) SGS
b) Zusammengesetzter Behälter
m 22 = X 1
q 23 = X 2
m 22 = X 3
q 23 = X 4
In beiden Fällen sind zwei zusätzliche statische Unbestimmte einzuführen. Im SGS
(Bild 5.28a 2), um die Biegelösung zu erfassen, die aus dem Dickensprung resultiert und
im SGS (Bild 5.28b 2), um die Biegestörung zu erfassen, die sich durch das biegesteife
Zusammenwirken der Teilschalen ergibt.

5.4 Membrantheorie von Allgemeinen Schalen
Die Membrantheorie ist eine statisch bestimmte Schalentheorie, die nur den Schei–
benanteil enthält. Biegung darf im Rahmen dieser Theorie nicht auftreten, so daß der
Plattenanteil entfällt. Wegen der gekrümmten Mittelfläche können bei Membranschalen
Flächenlasten senkrecht zur Fläche allein durch Scheibenkräfte aufgenommen werden.
Der Unterschied zwischen Scheiben und Membranschalen ist im (Bild 5.29) dargestellt.
(Bild 5.29a) zeigt die Verhältnisse bei ebenen Scheiben und (Bild 5.29b) bei gekrümmten
Membranschalen.
(2)
n 22
p 2
p 1
n 21 = n 12
n 12
n 11
(1)
Drei Kräfte (n 11 , n 22 , n 12 = n 21 )
und zwei unabhängige Kräfte–
gleichgewichtsbedingungen in
(1)– und (2)–Richtung ergeben
ein 1–fach statisch unbestimmtes
System.
Bild 5.29 : Unterschied zwischen Scheiben und Membranschalen
– 5 / 38 –
(2)
n 22
n 21 = n 12
p 3
p 2
p 1
n 12
n 11
(1)
(3): Normale der Mittelfläche
Drei Kräfte (n 11 , n 22 , n 12 = n 21 )
und drei unabhängige Kräfte–
gleichgewichtsbedingungen in
(1)–, (2)– und (3)–Richtung ergeben
ein statisch bestimmtes System.
a) Ebene Fläche: Scheibe b) Gekrümmte Fläche: Membranschale
Damit keine Biegung auftritt, ist die Lagerung von Schalen als Membranlagerung auszubilden,
die nur Kräfte in der Schalenfläche aufnehmen darf, um Querkräfte und Momente
zu vermeiden. Auch dürfen keine Einzelkräfte angreifen, da die Krafteinleitung
lokal ebenfalls eine Biegewirkung auslöst.

5.4.1 Kräftegleichgewicht
In der (1)– und (2)–Richtung in der Tangentenfläche von Membranschalen gilt
n �� � � � p � � 0. (5.33)
Gleichung (5.33) ist eine Erweiterung der Scheibengleichung n�� ,� � p � � 0. Die partielle
Ableitung n�� ,� � �n�� �n��
��� �
�x� erfaßt die Betragsänderung des Kraftvek–
tors n � n���a� � a �. � Die Richtung �a� � a � � ist konstant, weil bei Scheiben die kör-
perfesten Koordinaten �� 1 , � 2� mit der Basis a 1 und a 2 und die ortsfesten Koordina-
ten (X 1 , X 2 ) mit der konstanten Basis �i 1 � i 2 � zusammenfallen.
Bei Schalen ist dies nicht der Fall, so daß nun auch die Änderung der Basis
(a 1 und a 2) erfaßt werden muß. Anstelle der partiellen Ableitung n �� ,� � �n��
daher die kovariante Ableitung
n �� � �� n �� ,� � n �� � � �� � n �� � � ��
– 5 / 39 –
��� ist
(5.34)
zu bilden, um die Betrags– und Richtungsänderung von Kraftvektoren zu erfassen.
Die kovariante Ableitung enthält neben der partiellen Ableitung zur Erfassung der Betragsänderung
zwei zusätzliche Terme, um den Einfluß der Orts– und Richtungsabhängigkeit
der veränderlichen Basis zu erfassen. Die Transformationskoeffizienten �� ��
werden als Christoffel–Symbole bezeichnet.
In der (3)–Richtung senkrecht zur Tangentenfläche von Membranschalen gilt
b �� n �� � p 3 � 0. (5.35)
Gleichung (5.35) fehlt in der Theorie ebener Scheibentragwerke. Sie kann wegen der
Umlenkwirkung durch die Flächenkrümmung b �� nur bei Schalen auftreten (Bild 5.30).
Bei ebenen Flächentragwerken muß sie durch die Plattentheorie ersetzt werden.
(3): Normale
n ��
links
Bild 5.30 : Umlenkwirkung bei Membranschalen
p 3
Flächen–
krümmung b ��
n ��
rechts
b �� n ��

5.4.2 Kovariante Ableitung und Krümmung
Im (Bild 5.31) ist die Einbettung der Schalenfläche im dreidimensionalen Raum dargestellt.
i 1
X 1
X 3
i 3
i 2
X 2
a 3
(Ortfeste Basis)
a 2
R � (Ortsvektor)
a 1
– 5 / 40 –
� 3
(Körperfeste Basis)
� 1
Körperfeste Flächenkoordinaten � � , � � 1, 2
mit der Basis a 1 , a 2 , a 3 .
Ortsfeste Raumkoordinaten X i ,i� 1, 2, 3
mit der Basis i 1 , i 2 , i 3 .
Bild 5.31 : Einbettung der Schalenfläche im Raum
Die Einbettung ist durch die Parameterabbildung mit dem Ortsvektor
X 1 � X 1 (� 1 , � 2 )
R = X 2 � X 2 (� 1 , � 2 )
X 3 � X 3 (� 1 , � 2 )
(5.36)
eindeutig festgelegt. Mit Gl. (5.36) ist die Geometrie beliebiger Schalenflächen vollständig
bekannt.
Körperfeste Basis in der Tangentenfläche:
a� � �R
�� � � R, � , � � 1, 2 .
(5.36.1)

Körperfeste Einheitsbasis in Richtung der Normalen zur Tangentenfläche:
a 3 � a 1 � a 2
�a 1 � a 2 � .
– 5 / 41 –
(5.36.2)
Die körperfesten Koordinaten (� 1 , � 2 ) stimmen in der Regel nicht mit den Bogenkoordinaten
(s 1 , s 2 ) überein. Sie werden zur Unterscheidung als Tensorkoordinaten bezeichnet.
Gl. (5.36.1) definiert daher keine Einheitsvektoren. Der Normalenvektor
Gl. (5.36.2) ist dagegen als Einheitsvektor definiert. Die Umrechnung von Gl. (5.36.1)
auf Einheitsvektoren ist mit dem Maßtensor
a�·a � � a �� �
a 11
a 21
a 12
a 22
=
a 1 ·a 1 , a 1 ·a 2
a 2 ·a 1 , a 2 ·a 2
(5.37)
vorzunehmen, der die Schalenfläche durch Skalarprodukte der Basis ausmißt. Die Determinante
von Gl. (5.37) errechnet sich zu
a � det(a �� ) � a 11 a 22 � (a 12 ) 2 .
Die Inverse des Maßtensors a �� ist durch
�a�� � �a ��� � � � �
Kronecker–Symbol = Einheitsmatrix.
� � � � 1
� � � � 0
Inverse = Hochgestellte Indizes.
definiert. Das Ausschreiben führt auf die explizite Form
a 11
a 21
a 12
a 22
=
a 11 a 12
a 21
1 0
0 1
a 22
.
= 1 a
a 22 � a 21
� a 12
a 11
= a �� .
Die Determinante des inversen Maßtensors Gl. (5.40) errechnet sich zu
a ~ � det(a �� ) � 1 a .
(5.38)
(5.39)
(5.40)
(5.41)

Mit dem inversen Maßtensor Gl. (5.39) kann man nun eine zweite Basis definieren, die
orthogonal zur ersten Basis Gl. (5.36) steht. Aus Gl. (5.39)
erhält man
und
�a�� � �a ��� � a�·a��a ��� � a�·a � � � � �
a � � a�a �� (5.42.1)
a3 � a1 � a2 �a1 � a2� � a3 . (5.42.2)
Zur Unterscheidung der Basen bezeichnet man Gl. (5.39) als kovariante Basis und
Gl. (5.42) als kontravariante Basis. Weil nach Gl. (5.42.2) die Einheitsnormalen der
Basen zusammenfallen, entsteht Gl. (5.42.1) aus Gl. (5.36.1) durch eine Drehung um
die Normale. Wegen der Orthogonalität der Basen gilt speziell a 1 � a 2 und a 2 � a 1
(Bild 5.32).
a 3 � a 3
a 2
Bild 5.32 : Ko– und kontravariante Basis der Schalenfläche
a 1
a 2
a 1
Die Einführung von unterschiedlichen Basen ist nur in allgemeinen Tensorkoordinaten
sinnvoll. Sie vereinfacht die allgemeine Beschreibung von Schalentheorien (hier der
Membrantheorie) erheblich. In Bogenkoordinaten mit Einheitsvektoren sind alle Basen
gleich. Die Bemessungsgrößen müssen immer in Bogenkoordinaten angegeben werden.
Die Einheitsvektoren der Basen werden zur Unterscheidung durch geklammerte Indizes
gekennzeichnet. Man erhält sie, indem man die allgemeinen Basen durch die zugeordneten
Maßzahlen dividiert.
– 5 / 42 –
� 1
� 2

Einheitsvektoren der kovarianten Basis:
a (1) � a1 �
a 11
, a (2) � a2 �
, a (3) � a3 �
a22 �a1 � a �
2
�a
Einheitsvektoren der kontravarianten Basis:
a (1) � a1
�
a 11
, a (2) � a2
�
a 22
– 5 / 43 –
. (5.43.1)
, a (3) � a (3) � a 3 . (5.43.2)
Um die Änderung der Basis zu bestimmen, wird ein Ansatz gemacht, der die Änderung
der Basis auf die Basis selbst bezieht. Für die kovariante Basis Gl. (5.36) gilt
und
�a�
��� � a�, � � ��
�� a� � �3 �� a3 (5.44.1)
�a3 ��� � a3, � � ��
3� a� � �3 3� a3 . (5.44.2)
Die Transformationskoeffizienten, die mit den Christoffel–Symbolen der kovarianten
Ableitung bzw. der Krümmung übereinstimmen, erhält man durch Überschieben (Bildung
von Skalarprodukten) mit der kontravarianten Basis �a � , a 3� die orthogonal zur
kovarianten Basis �a�, a 3 � steht. Die Bildung der Skalarprodukte von links ergibt
und
a � ·a �, � � � �
�� a� ·a� � � 3
�� a� ·a 3 , (5.45.1)
a 3 ·a �, � � � �
�� a3 ·a� � � 3
�� a3 ·a 3 , (5.45.2)
a � ·a 3, � � � �
3� a� ·a� � � 3
3� a� ·a 3
(5.45.3)
a 3 ·a 3, � � � �
3� a3 ·a� � � 3
3� a3 ·a 3 . (5.45.4)
Mit a � ·a� � � � � (1 � � � � und 0 � � � �), a� ·a 3 � 0, a 3 ·a� � 0, a 3 ·a 3 � 1 und
a 3 ·a 3, � � 0 folgt aus Gl. (5.45)
und
� �
�� � a� ·a �, � , � �
3� � a� ·a 3, �
(5.46.1)
�3 �� � a3 ·a�, � � b�� , �3 � 0 . (5.46.2)
3�

Das Christoffel–Symbol �� erfaßt die Änderung der tangentialen Basis in der Tangen-
��
tenfläche und das Christoffel–Symbol �3 die Änderung senkrecht zur Tangenten–
��
fläche, also in der Normalen– oder Krümmungsfläche. Dieses Symbol wird daher auch
als Krümmungstensor b�� bezeichnet. Das Auschreiben mit (�, �, �) � 1, 2 ergibt
acht Christoffel–Symbole
� �
�� �
� 1 11
� 1 21
� 1 12
� 1 22
und vier Krümmungsterme
b �� �
b 11
b 21
b 12
b 22
.
� 2 11
� 2 21
� 2 12
� 2 22
– 5 / 44 –
(5.47)
(5.48)
Das Christoffel–Symbol �� erfaßt die Änderung der Schalennormalen in der Tangen-
3�
tenfläche und das Christoffel–Symbol �3 die Änderung senkrecht dazu in Richtung
3�
der Normalen, die Null wird, weil bei Flächen in dieser Richtung keine Änderung auftreten
kann.
Es gilt wegen a 3 ·a� � a 3 ·a� � 0 auch �a 3 ·a� � , � � a 3, � ·a� � a 3 ·a �, � � 0 und damit
und
� 3
�� � a 3 ·a �, � ��a�·a 3, � � b ��
(5.49.1)
�� 3� � a� ·a3, � � a�� a�·a3, � ��a�� b�� ��b� . (5.49.2)
�
Der Ausdruck
b� � � b�� a�� b
� (5.50)
1 1 b1 2
b 2 1
definiert die Krümmung in physikalischen Bogenkoordinaten.
b 2 2
Die allgemeinen Gleichgewichtsbedingungen der Membrantheorie Gl. (5.33) und
Gl. (5.35) können nun für spezielle Geometrien ausgewertet werden. Dies soll am Beispiel
von Rotationsschalen erfolgen.

5.4.3 Rotationsschalen
5.4.3.1 Allgemeine Rotationsschalen
Die Klasse der Rotationsschalen umfaßt sechs Schalenformen unterschiedlicher Geometrie:
Zylinder, Kegel, Kugel, Torus, Paraboloid, Hyperboloid. Die Geometrie der
Schalenfläche von Rotationsschalen kann zunächst einheitlich für alle Schalenformen
in den Flächenkoordinaten � 1 � Winkel in Ringrichtung und � 2 � Länge entlang der
Rotationsachse angegeben werden (Bild 5.33).
Breitenkreis
� 2
X 3
R(� 2 )
Bild 5.33 : Geometrie von Rotationsschalen
R
a 2
� 1
– 5 / 45 –
a 1
a 3
X 1
Rotationsachse
X 2
Meridian

Mit der Parameterabbildung
R �
R�� 2� cos � 1
R�� 2� sin � 1
� 2
sind dann auch die geometrischen Kennwerte
und
a �� �
b �� �
� �
�� �
a 11
0
b 11
0
0
a 22
0
b 22
0 � 1 12
� 1 21
0
1
a
0
11
, a
1
0 a22 �� � ,
, b � � �
� 2 11
0
0
� 2 22
b
0
1 1 � b11 a11 – 5 / 46 –
0
b 2 2 � b 22
a 22
(5.51)
bekannt. Da bei Rotationsschalen die Flächenkoordinaten �1 und �2 orthogonal zueinander
stehen und Rotationsflächen keine Verwindung aufweisen, entfallen die gemischten
Terme (a12 ,a21 ,a12 ,a21 ) und (b 12 ,b21 ,b1 2 ,b2 1 ) im Maß– und Krümmungstensor,
womit sich auch die Anzahl der Christoffel–Symbole halbiert.
Die Auswertung der Kräftegleichgewichtsbedingungen Gl. (5.33) und Gl. (5.35) ist unter
Beachtung der Summationsregel vorzunehmen. Das System der partiellen Differentialgleichungen
läßt sich sehr übersichtlich in Matrizenform darstellen.
� 1
� 2 11
b 11
0
� 2 � � 1 12 � 2 �2 22
b 22
� 2 � 3 � 1 12 � �2 22
� 1
0
n 11
n 22
n 12 � n 21
=
� p 1
� p 2
� p 3
(5.52)
Die partiellen Ableitungen sind als Operatoren definiert. Es ist daher in Gl. (5.52) nicht
nur die Matrizenmultiplikation sondern auch die Operation durchzuführen. Z.B. bedeutet
�1n11 � �n11
u.s.w.
��1

Bei den Kräften und Einwirkungen in Gl. (5.52) handelt es sich um Tensorgrößen. Sie
sind daher mit dem Maßtensor auf physikalische Bemessungsgrößen umzurechnen.
Die Kennzeichnung ist wie bei der Bildung der Einheitsvektoren durch Klammern der
Indizes vorzunehmen.
und
n�� � n(��)
a���
p � � p(�)
�
� a ��
a��
, p 3 � p(3)
�a
– 5 / 47 –
(5.53.1)
. (5.53.2)
Die Umrechnung erfolgt in der Regel nach der Integration von Gl. (5.52). Da die Einwirkung
immer in physikalischen Größen definiert ist, muß sie vorab mit Gl. (5.53.2) auf
tensorielle Einwirkungen umgerechnet werden.
Bei Rotationsschalen kann man Gl. (5.52) wegen der einfachen Geometrie auch vor der
Integration auf physikalische Größen umschreiben, indem man Gl. (5.53) in Gl. (5.52)
einsetzt. Als Ergebnis erhält man das Gleichungssystem in der Form
d 1
� �
b 1 1
0
d 2 � �
b 2 2
d 2 � 2 �
d 1
0
n (11)
n (22)
n (12) � n (21)
=
� p (1)
� p (2)
� p (3)
.
(5.54)
Die Ableitungen in Richtung der Bogenlänge s 1 (Breitenkreis) und s 2 (Meridian) sind
durch
d1 � �1 �a11
und d2 � �2 �a22
definiert und das modifizierte Christoffel–Symbol durch
� � �1 12
�a22
(5.55.1)
. (5.55.2)
Die weitere Vorgehensweise soll am speziellen Beispiel der Geometrie einer Kugelschale
vorgestellt werden.

5.4.3.2 Kugelschale
Die Geometrie der Kugelschale ist im (Bild 5.34) dargestellt. (Bild 5.34a) zeigt einen
Punkt P auf dem Meridian in der (X 1 � X 3 ) �Ebene und (Bild 5.34b) den zugehörigen
Breitenkreis parallel zur (X 1 � X 3 ) �Ebene auf der Höhe des Punktes P.
a) Meridian
X 3
R K cos � 2
Bild 5.34 : Geometrie einer Kugelschale
P
P
�2 �1 RK sin �2 X 1
– 5 / 48 –
X 3
b) Breitenkreis
�R K cos � 2� cos � 1
�R K cos � 2� sin � 1
R K cos � 2
Zur Beschreibung der Kugelgeometrie ist es einfacher, zwei Winkelkoordinaten einzuführen,
nämlich den Winkel � 1 im Breitenkreis (Bild 5.34b) und den Winkel � 2 im
Meridian (Bild 5.34a). Der Ortsvektor zum Punkt P auf der Kugel ist dann durch
R �
X 1 � R K cos � 2 cos � 1
X 2 � R K cos � 2 sin � 1
X 3 � R K sin � 2
X 1
(5.56)
gegeben. Mit Gl. (5.56) kann man alle benötigten geometrischen Daten der Kugelschale
ermitteln.
a 1 � R ,1 �
� R K cos � 2 sin � 1
R K cos � 2 cos � 1
0
� R K sin � 2 cos � 1
, a2 � R ,2 � � RK sin � ,
2 sin �1 R K cos � 2

a �� � a�·a � �
�a11 � RK cos �2 ,
�a22 � RK ,
� 2 a � RK cos �2 ,
b �� � a 3 ·a �,� �
� � �1 12
�a22
� a1 ·a1,2 �a22
2
�RK cos �2� 0
� R K cos 2 � 2
0
� a11 ·a1 ·a1,2 �a22
0
R 2 K
0
� R K
– 5 / 49 –
, a�� 1
2
�RK cos �2� �
1 ,
R2 0
0
K
a3 � a1 � a2 �a ,
cos � 2 cos � 1
� cos � ,
2 sin �1 sin � 2
� 1
b� � � a�� RK b�� � ,
�� 1
tan �
RK 2 .
0
0
�
1
Das Differentialgleichungssystem der Membrantheorie speziell für Kugelschalen ergibt
sich damit zu
�1 RK cos �2 0
�
tan �2
R K
� 1
R K
� 2
R K
�
� 1
R K
tan �2
R K
�2 RK �
2 tan �2
R K
� 1
R K cos � 2
0
n (11)
n (22)
n (12) � n (21)
=
R K
� p (1)
� p (2)
� p (3)
.
(5.57)

Die Lösung von Gl. (5.57) soll beispielhaft für rotationssymmetrische Lastfälle erfolgen.
Dazu gehören u.a. die Lastfälle Eigengewicht (g), Schnee (s) und Innendruck (p). Dann
gilt � 1 � 0, p 1 � 0 und n (12) � n (21) � 0, so daß sich die Membrantheorie der Kugelschale
weiter vereinfacht. Aus Gl. (5.57) folgt
�
tan �2
R K
� 1
R K
� 2
R K
�
� 1
R K
tan �2
R K
n (11)
n (22)
– 5 / 50 –
=
� p (2)
� p (3)
Die zweite Gleichung von (5.58) ist eine rein algebraische Gleichung.
.
(5.58)
n (11) � n (22) ) � R K p 3 . (5.59)
Gl. (5.59) kann als Faßformel der Kugel interpretiert werden. Damit ist die Beanspruchung
in der Summe bekannt. Unbekannt bleibt die Aufteilung der Kräfte in Richtung
des Breitenkreises und des Meridians. Dies muß daher die Integration der ersten Gleichung
liefern. Nach der Multiplikation mit R K cos � 2 erhält man den Ausdruck
sin � 2 n (11) � cos � 2 n (22) ,2 � sin �2 n 22 ��p 2 R K cos � 2 .
Die Anwendung der Kettenregel ergibt
�cos � 2 n (22)� ,2 ��sin � 2 n (22) � cos � 2 n (22) ,
so daß man nach dem Einsetzen von Gl. (5.59) zur Elimination der Kraft n (11) eine Differentialgleichung
für die Unbekannte Kraft n (22) erhält.
�cos � 2 n 22� ,2 � sin � 2 n (22) ��R K �p 2 cos � 2 � p 3 sin � 2� .
Die Multiplikation mit cos � 2 ergibt
cos � 2�cos � 2 n (22)� ,2 � sin � 2 cos � 2 n (22) ��R K cos � 2�p 2 cos � 2 � p 3 sin � 2�
und das nochmalige Anwenden der Kettenregel
�cos 2 � 2 n (22)� ,2 � cos � 2 �cos � 2 n (22)� ,2 � sin � 2 cos � 2 n (22) ,
so daß die Differentialgleichung zur Berechnung von n (22) die integrierbare Form
�cos 2 � 2 n (22)� ,2 ��R K cos � 2 �p 2 cos � 2 � p 3 sin � 2�

annimmt. Die Durchführung der Integration ergibt die Lösung
n (22) �� RK cos2 �2 ��p �2 2 cos2 �2 � p 3 sin �2 cos �2�d�2 � C . (5.60)
Mit Gl. (5.59) und Gl. (5.60) ist die Membranlösung für Kugelschalen unter rotationssymmetrischer
Flächenlasten p 2 und p 3 bekannt. Gl. (5.60) läßt sich durch das Schnittprinzip,
nämlich durch die Bildung des vertikalen Gleichgewichts in einfacher Weise
kontrollieren. Im Breitenkreisschnitt eines beliebigen Meridians (Bild 5.35) sind die Zusammenhänge
zur Bildung des Gleichgewichts in vertikaler Richtung (Index v) dargestellt.
n (22)
v
n (22)
Nv, Pv
R K cos � 2
Bild 5.35 : Breitenkreisschnitt eines beliebigen Meridians
– 5 / 51 –
R K
p 2
� 2
p v
p 3
Meridianschnitt
Meridian im
Breitenkreisschnitt
Die resultierende Einwirkung der Flächenlasten p 2 und p 3 in vertikaler Richtung errechnet
sich in einem Meridianschnitt zu
Pv �� A
p v dA .
A ist die Schalenfläche unterhalb des Meridianschnitts, vgl. (Bild 5.35). Die vertikale
Flächenlast p v (kN/m 2 ) ist durch die Projektion
Pv � cos � 2 p 2 � sin � 2 p 3

ekannt und das Differential der Schalenfläche durch das Produkt der Differentiale der
Bogenkoordinaten
dA � ds1ds2 � ��a11 d�1� � ��a22 d�2� � a � d�1d�2 � R2 K cos �2d�1d� 2 .
Die Auswertung des Flächenintegrals ergibt mit
� 2�
0
d� 1 � 2�
den Ausdruck
Pv � 2� R 2 K � � 2
�p 2 cos 2 � 2 � p 3 sin � 2 cos � 2�d� 2 .
Die vertikale Komponente n (22)
v (kN�m) der Schnittkraft n (22) im betrachteten Meridianschnitt
ist durch die Projektion
n (22)
v
� cos �2 n (22)
bekannt. Die Resultierende erhält man durch Multiplikation mit der Bogenlänge
�2� R K cos � 2� des zugehörigen Breitenkreises zu
Nv � cos � 2 n (22)�2� R K cos � 2� � 2� R K cos 2 � 2 n (22) .
Aus dem Gleichgewicht der resultierenden Kräfte
Nv � Pv � 0 � Nv ��Pv
folgt der Ausdruck
n (22) �� RK cos2 �2��p �
2 cos2 �2 � p 3 sin �2 cos �2�d�2 ,
der bis auf die Integrationskonstante vollständig mit Gl. (5.60) übereinstimmt.
– 5 / 52 –

5.4.3.3 Lastfall Innendruck einer Vollkugel
Für den speziellen Lastfall Innendruck einer Vollkugel, z.B. eines Fußballs, mit p 2 � 0
und p 3 � 0 ist die Lösung Gl. (5.59) und Gl. (5.60) auszuwerten. Der Lastfall ist im
(Bild 5.36) dargestellt. (Bild 5.36a) zeigt die Einwirkung entlang des Meridians und
(Bild 5.36b) entlang des Breitenkreises.
R K
a) Meridian
X 3
n (22) X 2
p (3) p (3)
�2
X 1
Bild 5.36 : Lastfall Innendruck einer Vollkugel
– 5 / 53 –
R K
b) Breitenkreis
n (11)
Die Summe der Membrankräfte ergibt sich nach Gl. (5.59) aus der Faßformel, also aus
Radius mal Innendruck. Bei der vollsymmetrischen Kugel ist zu erwarten, daß sich der
Einwirkungsteil R K p (3) je zur Hälfte auf Breitenkreis und Meridian verteilt. Die Lösung
wäre demnach
und
n (11) � 1
2 R K p3
n (22) � 1
2 R K p(3) .
Zur Bestätigung wird Gl. (5.60) ausgewertet. Die Integration mit p 2 � 0 ergibt
p 3 � � 2
sin � 2 cos � 2 d� 2 � p 3 � � 2
Damit erhält man für n (22) den Ausdruck
n (22) � R K p3
2
� C
�� 1
2 cos2 �2� d�
,2
2 �� 1
2 cos2 �2 � 1
X 1

und für n (11) nach Einsetzen von n (22 ) in Gl. (5.59) den Ausdruck
n (11) � R K p3
2
� C.
Im oberen Scheitelpunkt der Kugel gilt � 2 = 90°, vgl. (Bild 5.34a). In diesem Punkt fallen
die Richtung von Breitenkreis und Meridian zusammen (Bild 5.37).
n (11)
n (22)
Bild 5.37 : Scheitelpunkt einer Kugel
– 5 / 54 –
Breitenkreis
Meridian
Aus Gleichgewichtsgründen muß hier daher n (11) = n (22) werden. Die Integrationskonstante
C muß demnach Null werden, um dies zu erreichen. Die mathematische Lösung
stimmt also mit der anschaulichen Lösung überein.

Teil 6: Gitterrostmethode (GRM)
6.1 Baustatischer Lösungsansatz mit Gitterrosten
Die programmunterstützte Bearbeitung von statischen Problemen ist als Regel–
fall der Ingenieurpraxis anzusehen. Im Konstruktiven Ingenieurbau dominieren
Programme zur Untersuchung von Stabtragwerken. Sie beruhen i.a. auf der rechner–
orientierten Variante des Weggrößenverfahrens. Es wird z.B. in der Lehrveranstaltung
Statik III behandelt und dort als Verfahren der Stabsteifigkeiten bezeichnet /12/. Die Berechnung
kann mit allen Programmen erfolgen, die in ihrer Elementbibliothek ebene
oder räumliche Stäbe enthalten.
Baukonstruktionen setzen sich in der Regel aus stabförmigen und flächigen Tragelementen
zusammen. Wandscheiben und Deckenplatten sind neben Stützen und Balken
in fast allen Hochbauten anzutreffen. Sie bilden wichtige Tragelemente, um Gebäude
auszusteifen. Zur Festlegung der Aussteifungskonzeption ist es daher vielfach erforderlich,
statische Systeme zu verwenden, die aus einer Kombination von stabförmigen
und flächigen Tragelementen bestehen. Ein Programm zur Untersuchung von Stabtragwerken
ist i.a. immer verfügbar. Es stellt sich daher die Frage, wie flächige Tragelemente
in statischen Systemen erfaßt werden können, ohne den Anwendungsbereich
der Stabstatik zu verlassen.
Dies gelingt mit dem baustatischen Lösungsansatz der GRM. Gitterroste sind Stab–
modelle, die das flächige Tragverhalten von Scheiben und Platten in baustatisch gleichwertiger
Weise erfassen. In beiden Modellen müssen sich also äquivalente Gleichgewichts–
und Verträglichkeitszustände einstellen. Die Ableitung von Gitterrosten ist
daher konsequent auf der Grundlage eines Vergleichs der zugehörigen Berechnungstheorien
durchzuführen. Ziel ist es, Scheiben durch ebene Fachwerke und Platten durch
liegende Rahmenwerke bzw. Trägerroste zu ersetzen, um sie in das Konzept der Stabstatik
einbeziehen zu können, ohne daß sich ein grundsätzlicher Verlust an flächiger
Tragwirkung einstellt.
Wandscheiben sind aber auch zur Verteilung konzentrierter Lasten erforderlich und
Deckenplatten zur Abtragung von Flächenlasten. Zur Untersuchung dieser lokalen
Wirkungen kann man zwar auch die GRM verwenden, der Aufwand wächst aber überproportional
an. In solchen Fällen erweist es sich als sinnvoller, die FEM einzusetzen,
die Scheiben und Platten direkt als flächige Tragelemente modelliert. Eine kurze Einführung
in die FEM der Flächentragwerke erfolgt im Teil 7.
Die Abschnitte 6.2.2 und 6.3.2 sind besonders wichtig. In ihnen wird die Ermittlung
der Querschnittswerte der Gitterroststäbe behandelt, damit sie Scheiben und Platten
gleichwertig ersetzen. Das Ergebnis ist im (Bild 6.38) zusammengestellt. Darüber hinaus
ist noch der Abschnitt 6.2.4 von Interesse. Er zeigt auf, wie man aus den Schnitt–
größen der Gitterroststäbe die Schnittgrößen von Flächentragwerken ermittelt. Das Ergebnis
dieser Betrachtung ist im (Bild 6.39) zusammengestellt. Die restlichen
Abschnitte haben begleitenden Charakter. Sie haben vorrangig die Aufgabe, das Verständnis
der GRM zu erhöhen.
– 6 / 1 –

6.2 Scheibe und Fachwerk
6.2.1 Einleitung
Die analytische Lösung von baupraktischen Scheibenproblemen mit Hilfe der Scheibengleichung
∆∆F = 0 ist nur im sehr begrenzten Umfang möglich, vgl. Teil 3: Scheibentheorie.
Es sind zwar hinreichend viele Fundamentallösungen der Scheibengleichung
bekannt, es gelingt aber nur unter starken Einschränkungen, die zulässigen
Spannungsfunktionen F auch an die vorliegenden Randbedingungen anzupassen. Es
ist daher sinnvoll, Überlegungen darüber anzustellen, ob sich das Scheibenproblem
nicht auf bekannte baustatische Vorgehensweisen zurückführen läßt, wobei man natürlich
sofort an ebene Fachwerke denkt, da beide Modellsysteme ihre Lasten ausschließlich
über Dehnbeanspruchung abtragen.
Im (Bild 6.1) ist am Beispiel einer Stahlbetonwand dargestellt, wie die Modellanalogie
zwischen Scheibenkonstruktion und Fachwerk aussehen könnte. (Bild 6.1a) zeigt
das statische System der Wandscheibe als Kontinuum nach der Scheibentheorie und
(Bild 6.1b) als Fachwerk nach der Gitterrosttheorie. Wenn es gelingt, den Querschnitt
der kontinuierlichen Wandscheibe durch gleichwertige Ersatzflächen der Gitterroststäbe
im Fachwerk zu ersetzen, so kann an Stelle des kontinuierlichen Scheibenproblems
das diskrete Fachwerkproblem gelöst werden, um die Bemessungsgrößen der
Wandscheibe zu ermitteln. Die Vorteile einer solchen Vorgehensweise liegen auf der
Hand:
– Die Berechnung von ebenen Fachwerksystemen ist eine Standardaufgabe der
Baustatik und kann daher als bekannt vorausgesetzt werden. Die Durchführung
ist leicht programmierbar. Die Vielzahl der erforderlichen Fachwerkstäbe, die zur
wirklichkeitsnahen Erfassung der Scheibenwirkung notwendig sind, stellen daher
keine Einschränkung dar.
– Bei der Anwendung der Fachwerksanalogie entfallen konstruktive Einschränkungen,
da die Scheiben im statischen Berechnungssystem so abgebildet werden
können, wie sie im Bauwerk vorliegen.
– Der aufwendige mathematische Apparat, der zur Lösung von partiellen Differentialgleichungen
4–ter Ordnung erforderlich ist, entfällt ersatzlos. Er wird durch
ingenieurmäßige Betrachtungen ersetzt, die aus der Baustatik vertraut sind, wodurch
sich die anschauliche Kontrolle der Ergebnisse erheblich vereinfacht.
Der Erfolg der Idee, Scheibenprobleme über Fachwerksysteme zu lösen, hängt ausschließlich
von der Güte der Querschnittsflächen der Ersatzstäbe ab, da nur sie die statische
und geometrische Äquivalenz zwischen beiden Modellen gewährleisten. Ihre Ermittlung
steht daher im Mittelpunkt der weiteren Betrachtung.
– 6 / 2 –

h
L 2
n 2
b
X 2
X 1
L 1
a a
– 6 / 3 –
Rand–
einwirkung
Elastomere Auflager mit E–Modul E L
a) Kontinuum: Modell nach der Scheibentheorie
C 11
C 22
R
4
R
2
R
4
C 11
b) Fachwerk: Modell nach der Gitterrosttheorie
R = n 2 b
C 22
Bild 6.1 : Statische Systeme einer Stahlbetonwand
t
C 22 � E L at
h
C 11 � 0, 3C 22
Scheiben–
mittelfläche
E, ν
A n: Querschnitts–
fläche des n–ten
Fachwerkstabs.

6.2.2 Querschnittsflächen der Gitterroststäbe
Aus dem Scheibenmodell der Wandscheibe (Bild 6.1a) wird ein endlich begrenztes
Element (Bild 6.2a) herausgeschnitten und in den Schnitten die Scheibengrößen eingetragen.
n 11 , α 11
n 12 , α 12
X 2
Bild 6.2a : Scheibenelement
a
n 21 , α 21
Am Scheibenelement (Bild 6.2a) bedeuten:
(a,b) die Seitenlängen,
b
– 6 / 4 –
n 22 , α 22
n 22 , α 22
(n αβ ) die Scheibenkräfte mit n 12 = n 21 ,
n 21 , α 21
n 12 , α 12
n 11 , α 11
(ααβ) die Dehnungen des Scheibenelements mit α12 → (α12 + α21) und
α, β ... = 1, 2) die Indizierung der Flächenkoordinaten.
In gleicher Weise wird aus dem Fachwerkmodell der Wandscheibe (Bild 6.1b) ein rechteckig
begrenztes Gitterrostelement (Bild 6.2b) herausgeschnitten, das sich aus sechs
Fachwerkstäben zusammensetzt. Die Diagonalen sind am Kreuzungspunkt nicht miteinander
verbunden.
X 1

X 2
Bild 6.2b : Gitterrostelement
a
N 1 D
1
D
N 1, A 1
N 1 A
�
N 2 D
α 3 3 α
α
N
α
3, A3 �
�
A N2, A2 B
N 2 A
2
b = a tanα
Da es sich im vorliegenden Fall um ein rechteckiges und daher symmetrisches Gitter–
rostelement handelt, sind jeweils zwei Seitenstäbe und die beiden Diagonalen gleich,
so daß nur drei unabhängige Stäbe auftreten. Am Gitterrostelement (Bild 6.2b) bedeuten:
n = 1, 2 und 3 die Stabnummern,
A, B, C und D die Eck– oder Kontaktknoten,
N 1, N 2 und N 3
A 1, A 2 und A 3
N 1 K und N2 K
die Stabkräfte,
die Stabquerschnittsflächen,
– 6 / 5 –
2
�
N 2 C
C
N 2 B
n =
N 1 C
1
N 1 B
mit K = A, B, C und D die resultierenden Knotenkräfte
in Richtung der X 1 – und X 2 –Koordinaten und
(a, b) die Seitenlängen des Gitterrostelements, die mit den
Längen des Scheibenelements übereinstimmen.
(α) ist der Neigungswinkel der Diagonalstäbe, so daß
zwischen den Seitenlängen die Beziehung
b = a tanα gilt.
X 1

Es sind natürlich auch andere Gitterrostformen möglich, z.B. Dreiecke und Trapeze.
Aus didaktischen Gründen ist es aber sinnvoll, nur die einfachste Form, nämlich die
Rechteckform zu betrachten, da bei der Ableitung der Stabflächen bereits alle wesent–
lichen Überlegungen zum Tragen kommen und der Formelapparat noch überschaubar
bleibt, der sich bei Dreiecken und Trapezen erheblich komplizierter gestaltet.
Ziel der Betrachtung ist es, die vollständige statische und geometrische Äquivalenz
zwischen Scheiben– und Fachwerkmodell, abzuleiten, um Gleichgewicht und Verträglichkeit
als Grundforderungen der Baustatik wechselseitig zu erfüllen. Das Scheiben–
element (Bild 6.2a) ist durch kontinuierliche Schnitte von seiner Umgebung getrennt, in
denen die globalen, auf die X 1 – und X 2 –Koordinaten bezogenen Scheibengrößen n αβ
und ααβ wirken. Beim Gitterrostelement (Bild 6.2b) reduziert sich der Kontakt zur Umgebung
auf vier Eckknoten, da alle Stäbe lediglich in diesen Knoten zusammenstoßen.
Alle Einwirkungen auf das Gitterrost müssen daher über diese Knoten erfolgen, um sich
im Gitterrost verteilen zu können.
Die Kontaktkräfte der Gitterrostkanten sind aus globalen Gleichgewichtsbedingungen
mit den Scheibengrößen zu bestimmen, um die Forderung nach statischer Äquivalenz
erfüllen zu können. Sie sind im (Bild 6.3) dargestellt. Dabei ist zu beachten, daß die
Scheibenkräfte längenbezogene Größen darstellen. Zur Bildung der Resultierenden ist
also die Multiplikation mit den Längen der Schnittränder erforderlich, wobei das Verhältnis
b = a tanα eingeht, um nur mit einer Länge zu arbeiten.
X 2
X 1
N 1 D
D
n11 a
N 1 A
n 21 = n 12
a tanα
n21 = n12 A B
Bild 6.3a : Globales Kräftegleichgewicht in X 1 –Richtung
Nach (Bild 6.3a) ergeben sich die Knotenkräfte der X 1 –Richtung zu
und
N 1 A ��N1 C � 0.5a(n11 � tan� n 12 ) (6.1.1)
� N 1 B � N1 D � 0.5a(n11 � tan� n 12 ). (6.1.2)
– 6 / 6 –
C
N 1 C
N 1 B
n 11

X 2
X 1
N 2 D
D
a tanα
A B
N 2 A
n 22
Bild 6.3b : Globales Kräftegleichgewicht in X 2 –Richtung
– 6 / 7 –
N 2 C
C
n a 12 n12 n 22
In gleicher Weise können aus (Bild 6.3b) die Knotenkräfte der X 2 –Richtung bestimmt
werden.
und
N 2 A ��N2 C � 0.5a(tan� n22 � n 12 ) (6.1.3)
N 2 B ��N2 D � 0.5a(tan� n22 � n 12 ). (6.1.4)
Mit (6.1) sind die Kräfte bekannt, die als Reaktionsgrößen auf das Gitterrostelement einwirken.
Die statische Äquivalenz für das Gleichgewicht ist erfüllt, wenn die globalen
Knotenkräfte mit den lokalen Stabkräften im Gitterrost einen Gleichgewichtszustand bilden.
Die lokalen Gleichgewichtsbedingungen sind für jeden Kontaktknoten auszuwerten.
Für den Knoten A sind die Zusammenhänge im (Bild 6.4) dargestellt.
N 1 A
Globale Knotenkräfte (Aktion)
X 2
X 1
Bild 6.4 : Lokales Kräftegleichgewicht in X 1 – und X 2 –Richtung am Knoten A
N 1
α
A
N 2 A
N 2 B
N 3
N 2
Lokale Stabkräfte (Reaktion)

Es gilt
und
N 2
� N 3 sin� � N 1 A
– 6 / 8 –
(6.2.1)
N3cos� � N1 � N (6.2.2)
2 A .
Da das Gitterrost im vorliegenden Fall nur aus drei unabhängigen Stäben besteht und
aufgrund der Rechteckform doppeltsymmetrisch ist, ergeben sich aus den Gleich–
gewichtsbedingungen der Knoten B, C und D keine neuen Erkenntnisse. Das
Gleichungssystem (6.2) ist unterbestimmt, da nach (Bild 6.4) drei unbekannten Stab–
kräften nur zwei bekannte Knotenkräfte gegenüberstehen. Diese Bilanz korrespondiert
mit der Scheibentheorie, die 1–fach innerlich statisch unbestimmte Grundgleichungen
aufweist. Eine eindeutige Lösung ist daher nur möglich, wenn zusätzlich auch die kinematischen
und elastischen Bedingungen im Gitterrost erfüllt werden, so daß die Gleichwertigkeit
zwischen Scheiben– und Fachwerkmodell neben dem Gleichgewicht
zwangsläufig auch die Verträglichkeit einschließen muß.
Die lokale Verträglichkeit für die Stäbe n = 1, 2 und 3 ist aus der Stabstatik bekannt.
Zwischen Kinematik (Index K) und Material (Index M) gilt der Zusammenhang
� K n � � M n � 0
mit � M n � Nn
EAn
(6.3.1)
. (6.3.2)
� K n ist die kinematische und � M n die materialbedingte Dehnung der Gitterroststäbe. Der
Wert (EA n) drückt die lokale Stabsteifigkeit aus und enthält als Flächenparameter die
gesuchte Querschnittsfläche A n der Stäbe.
Die kinematische Stabdehnung �K n ist als Funktion der kinematischen Scheibendehnungen
�K zu ermitteln, die über die Kontaktknoten auf das Gitterrost einwirken und
��
von diesen geometrisch äquivalent aufgenommen werden müssen. Die Stabdehnung
und die Scheibendehnungen sind im (Bild 6.5) dargestellt. Der Zusammenhang zwischen
ihnen ist aus einer zweifachen Transformationsvorschrift abzuleiten, um die
Orts– und Richtungsänderung der zweidimensionalen Scheibendehnungen zu erfassen.
Die Ortstransformation ist im (Bild 6.5a) veranschaulicht. Im Flächenschnitt
, im Flächen-
X1 = konstant wirken entlang der Länge a die Komponenten �K 11 und �K 12
schnitt X2 = konstant wirken entlang der Länge b die Komponenten �K 21 und �K 22
und im schiefen Schnitt wirken entlang der Länge s die resultierenden Dehnungen � K 1
und � K 2 , die in Richtung der X1 – bzw. X 2 –Koordinate zeigen.

� K 11
� K 12
X 2 , u 2
Bild 6.5a : Ortstransformation
a
ϕ n � K 2
s
b
� K 21 � K 22
Wegen der Längenbezogenheit der Scheibengrößen gilt
und
– 6 / 9 –
ϕ n
n–ter Gitterroststab
� K 1
ϕ n
ϕ n
X 1 , u 1
� K s � � K a � � K b (6.4.1)
� K s � � K a � � K b . (6.4.2)
Mit den geometrischen Beziehungen
a � scosϕn und b � ssinϕn ,
die zwischen den Längen a, b und s und der Richtung ϕ n des n–ten Gitterstabs gelten,
folgt aus Gl. (6.4.1)
� K � � K cosϕn � � K sinϕn
und aus Gl. (6.4.2)
(6.5.1)
� K � � K cosϕn � � K sinϕn . (6.5.2)
Damit ist die Ortstransformation abgeschlossen, die sich auf den ersten Index von �K ��
bezieht. Im zweiten Transformationsschritt ist nun noch die Richtungstransformation
der resultierenden Dehnungen �K 1 und �K 2 vorzunehmen, die sich auf den zweiten Index
von �K bezieht. Sie ist im (Bild 6.5b) veranschaulicht.
��

X 2
Bild 6.5b : Richtungstransformation
Es gilt
� K 11
� K 12
a
� K 2
s
b
� K 21 � K 22
– 6 / 10 –
� K n
ϕ n
ϕ n
� K 1
� K 2 sinϕn
� K 1 cosϕn
� K n � � K cosϕn � � K sinϕn . (6.6.1)
Mit den Beziehungen (6.5.1) und (6.5.2) folgt aus Gl. (6.6.1) der Ausdruck
� K n � � K 11 cos2 ϕn � � K 22 sin2 ϕn � �� K 12 � �K 21 �sinϕncosϕn . (6.6.2)
Die resultierende Scheibengleitung ist gemäß (Bild 6.5c)
Bild 6.5c : Resultierende Scheibengleitung
durch
90° � �� K 12 � �K 21 �
90° � �� K 12 � �K 21 �
X 1
90° � �� K 12 � �K 21 �
90° � �� K 12 � �K 21 �
� K 12 � �� K 12 � �K 21 � (6.6.3)

definiert. Wird Gl. (6.6.3) in Gl. (6.6.2) eingesetzt, erhält man den Ausdruck
� K n � � K cos 2 ϕn � � K sin 2 ϕn � � K sinϕncosϕn . (6.6.3)
Die kinematischen Scheibendehnungen � K ��
sind über die Verträglichkeitsbedingung
der Scheibentheorie mit den Scheibenkräften nαβ verknüpft. Aus der Gleichheit der
kinematischen und materiellen Scheibendehnungen
� K ��
–
� M ��
� 0
folgt durch Ausschreiben die explizite Form der Scheibenverträglichkeit zu
� K 11
� K 22
� K 12
� 1
Et �n 11 � �n 22� � 0,
– 6 / 11 –
(6.7)
(6.7.1)
� 1
Et �n 22 � �n 11� � 0 , (6.7.2)
��2 (1 � �)
Et �n12 � 0 (6.7.3)
oder nach den Scheibenkräften aufgelöst
mit
n 11 � D�� K 11 � ��K 22 � , (6.7.4)
n 22 � D�� K 22 � ��K 11 � ,
n12 (1 � �)
� D� ��
2 K 12
D �
Et
�1 � � 2�
als Dehnsteifigkeitsfaktor der Scheibentheorie.
(6.7.5)
(6.7.6)
(6.7.7)
Es können nun zwei alternative Zustände an den Kontaktknoten des Gitterrostes vorgeschrieben
werden, um die Stabflächen A n aus der vollständigen statischen und geometrischen
Äquivalenz zwischen einem elastischen Scheiben– und einem elastischen
Fachwerkmodell bestimmen zu können. Der Vergleich kann entweder mit Hilfe eines
Einheitsspannungs– oder eines Einheitsverformungszustandes erfolgen. Für den Fall
isotroper Elastizität führen beide Vorgehensweisen auf identische Werte für die Stab–
flächen.
Im vorliegenden Fall wird dem Gitterrost über die Kontaktknoten an den Ecken ein Einheitsverformungszustand
eingeprägt, der sich aus
� K 11
� K 22
: Globale Scheibendehnung in X 1 –Richtung,
: Globale Scheibendehnung in X 2 –Richtung

und
� K 12
: Globale Scheibengleitung
zusammensetzt. Damit sind über Gl. (6.7.4 bis 6.7.6) auch die zugehörigen Scheibenkräfte
bekannt, die sich aus den Einheitsverformungen ergeben und die über die
Knotenkräfte nach Gl. (6.1.1 bis 6.1.3) auf das Gitterrost einwirken. Alle globalen Einwirkungsgrößen
auf das Gitterrostelement sind durch die Vorgabe von Einheitsverformungen
also eindeutig festgelegt. Wird Gl. (6.7.4 bis 6.7.6) in Gl. (6.1.1 und 6.1.3)
eingesetzt, ergibt sich
und
N1 A � 0.5aD���K 11 � ��K 22� (1 � �)
� tan�� ��
2 K 12� (6.8.1)
N2 A � 0.5aD�tan� ��K 22 � ��K 11� (1 � �) �� ��
2 K 12� . (6.8.2)
Die Aufnahme der Knotenkräfte Gl. (6.8.1 und 6.8.2) im Gitterrost ist durch die lokale
Gleichgewichtsbedingung Gl. (6.2.1 und 6.2.2) bekannt. Das Einsetzen von Gl. (6.8.1
und 6.8.2) in Gl. (6.2.1 und 6.2.2) führt auf
und
N2 � N3sin� � 0.5aD���K 11 � ��K 22� (1 � �)
� tan�� ��
2 K 12� (6.9.1)
N1 � N3cos� � 0.5aD�tan���K 22 � ��K 11� (1 � �) �� ��
2 K 12� . (6.9.2)
Da dieser Gleichgewichtszustand auch verträglich sein muß, gilt für die lokalen Stabkräfte
Gl. (6.3.1 und 6.3.2), die über Gl. (6.6.3) ebenfalls mit den globalen Einheitsverformungen
verknüpft sind, so daß durch das Einsetzen von Gl. (6.6.3) in Gl. (6.3.1) und
Gl. (6.3.1) in Gl. (6.3.2) die allgemeine Bestimmungsgleichung für die Stabkräfte
Nn � EAn�� K 11 cos2 ϕn � � K 22 sin2 ϕn � � K 12 sinϕncosϕn� (6.10)
folgt, die für die Stabwinkel ϕ n, n = 1, 2 und 3 auszuwerten ist, um sie in Gl. (6.9.1
und 6.9.2) einsetzen zu können. Die Stabwinkel sind durch die Geometrie des Gitter–
rostelementes (Bild 6.6) bekannt.
– 6 / 12 –

X 2
1
α
3
2
ϕ n
Bild 6.6 : Stabwinkel im Gitterrostelement
und
n–ter Gitterroststab
ϕ 1 � 90° , (6.11.1)
ϕ 2 � 0° (6.11.2)
ϕ 3 � 90° � � (6.11.3)
Gl. (6.11.1 bis 6.11.3) der Reihe nach in Gl. (6.10) eingesetzt, führt auf die Stabkräfte
und
N 1 � EA 1 � K , (6.12.1)
N 2 � EA 2 � K (6.12.2)
N 3 � EA 3 �� K 11 sin2 α � � K 22 cos2 α � � K 12 sinαcosα� , (6.12.3)
die in Gl. (6.9.1 und 6.9.2) eingesetzt werden, um die Bestimmungsgleichung für die
Stabflächen A 1, A 2 und A 3 zu erhalten. Gl. (6.12.1, 6.12.3 und 6.7.7) in Gl. (6.9.1)
eingesetzt, ergibt
A2�K 11 � A3��K 11sin2α � �K 22cos2α � �K 12sinαcosα�sinα �
� at
2�1 � �2�����K 11 � ��K 22� (1 � �)
� tan�� ��
2 K 12�
und Gl. (6.12.1, 6.12.3 und 6.7.7) in Gl. (6.9.2) eingesetzt, ergibt
A1�K 22 � A3��K 11sin2α � �K 22cos2α � �K 12sinαcosα�cosα �
� at
2�1 � �2���tan� ��K 22 � ��K 11� (1 � �)
�� ��
2 K 12� .
– 6 / 13 –
X 1
(6.13.1)
(6.13.2)

Die eingeprägten Einheitsverformungen �K 11 , �K 22 und �K 12 sind linear unabhängig
und müssen daher jeweils für sich erfüllt sein. Durch einen Koeffizientenvergleich ergeben
sich damit aus Gl. (6.13.1 und 6.13.2) zwei mal drei Gleichungen, um die Stabquerschnittsflächen
A1, A2 und A3 zu bestimmen.
Einheitsverformungszustand � K 11 :
Aus Gl. (6.13.1) folgt
A 2 � A 3 sin 3 � �� at
2�1 � � 2��
und aus Gl. (6.13.2)
A 3 sin 2 �cos� ��
Einheitsverformungszustand � K 22 :
Aus Gl. (6.13.1) folgt
A 3 cos 2 �sin� ��
und aus Gl. (6.13.2)
A 1 � A 3 cos 3 � ��
– 6 / 14 –
(6.14.1)
at tan��
2�1 � �2�� . (6.14.2)
at �
2�1 � �2�� at tan�
2�1 � �2�� .
Einheitsverformungszustand � K 12 :
Aus Gl. (6.13.1) folgt
A 3 sin 2 �cos� ��
at tan�
4(1 � �) �
und aus Gl. (6.13.2)
A3 sin �cos2� �� at � .
4(1 � �)
(6.14.3)
(6.14.4)
(6.14.5)
(6.14.6)

Da sechs Gleichungen für drei Unbekannte vorliegen, ist das Gleichungssystem überbestimmt.
Eine widerspruchsfreie Lösung ist daher nur unter einschränkenden Bedingungen
möglich. Die Gl. (6.14.2, 6.14.3, 6.14.5 und 6.14.6) sind Bestimmungs–
gleichungen für die Querschnittsfläche A 3 der Diagonalstäbe, wobei die Koeffizienten
von Gl. (6.14.2 und 6.14.5) und von Gl. (6.14.3 und 6.14.6) übereinstimmen. Aus der
Gleichheit der flächenfreien Koeffizienten folgt dann zwangsläufig, daß eine vollständige
statische und geometrische Äquivalenz zwischen elastischen Scheiben und elastischen
Fachwerken nur dann zu verwirklichen ist, wenn die Querdehnzahl den Wert
ν = 1/3 annimmt.
Aus (Gl. 6.14.2 und 6.14.5) folgt:
at tan��
2(1 � � 2 �
at tan�
) 4(1 � �)
und aus (Gl. 6.14.3 und 6.14.6)
at�
2(1 � � 2 ) �
at
4(1 � �)
→ 2� � 1 � � → � � 1
3
→ 2� � 1 � � → � � 1
3 .
Von den vier Gleichungen darf also nur eine verwendet werden. Zusammen mit den
Gl. (6.14.1 und 6.14.4) folgt mit ν = 1/3 das Gleichungssystem für die unbekannten
Querschnittsflächen der Fachwerkstäbe A 1, A 2 und A 3 in Matrizenform zu
A 1
A 2
0 1
A 3
sin 3 α
1 0 cos 3 α
0 0 sinα cos 2 α
– 6 / 15 –
Rechte Seite
9
16 at
9
at tanα
16
3
16 at
Die Auflösung von Gl. (6.14) führt auf die Bestimmungsgleichungen
und
A 1 � 3
16 at (3tan� � cotα) � A 0 f 1 ,
A 2 � 3
16 at �3 � tan 2 α� � A 0 f 2
A3 � 3
16 at
1
sinαcos2 � � A0f3 .
(Gl. 6.14.1)
(Gl. 6.14.4)
(Gl. 6.14.3)
(6.15.1)
(6.15.2)
(6.15.3)

Die Grundfläche aller Stäbe beträgt
A0 � 3
at ,
16
die sich in Abhängigkeit der Neigung der Diagonalstäbe durch die Faktoren
und
f 1 � 3tan� � cot� ,
f 2 � 3 � tan 2 �
f 3 �
1
sin�cos 2 �
– 6 / 16 –
(6.16.1)
(6.16.2)
(6.16.3)
(6.16.4)
verändert, um das scheibenförmige Tragverhalten im äquivalenten Fachwerkmodell
optimal zu erfassen.
Der Wertebereich der Bestimmungsgleichungen (6.15 bzw. 6.16) ist im (Bild 6.7) veranschaulicht.
Die Neigung der Diagonalstäbe soll die Grenzwinkel
30° ≤ α ≤ 60°,
(6.17.1)
nicht unter– bzw. überschreiten, da sich sonst negative Flächen einstellen, die zwar aus
mathematischer Sicht gewährleisten, daß die statische und geometrische Äquivalenz
zwischen elastischen Scheiben und elastischen Fachwerken erfüllt ist, die aber physikalisch
keinen Sinn ergeben und daher von der Konkurrenz ausgeschlossen werden
müssen.
Bei α = 45° sind die Flächen der vertikalen und horizontalen Stäbe gleich und die
der Diagonalstäbe um 2 � mal größer, was zu einer optimalen Flächenbelegung führt,
vgl. (Bild 6.7a). Bei 30° (Bild 6.7b) fallen die vertikalen und bei 60° die horizontalen
Stäbe aus, so daß der Kräftefluß hauptsächlich entlang der Diagnonalen verläuft. Die
anschauliche Deutung der 30°– und 60°–Systeme zeigt, daß die Gitterroste im Grenzzustand
zusätzlich durch äußere Lagerbedingungen stabilisiert werden müssen, um
kinematische Ketten zu vermeiden. Bei praktischen Problemen ist daher zu gewähr–
leisten, daß die zusätzlich erforderlichen Aussteifungselemente in Form benachbarter
Gitterroste vorliegen. Noch besser ist es, kinematische Gitterroste von vornherein zu
vermeiden. Dies gelingt, wenn der Diagnonalwinkel im Bereich
40° � � � 50°
gehalten wird, was sich ohne Schwierigkeiten immer verwirklichen läßt.
(6.17.2)

6
5
4
3
2
1
–1
–2
–3
–4
–5
–6
f
f 3
unzulässig
zulässiger Bereich
empfohlener Bereich
– 6 / 17 –
unzulässig
a) Abhängigkeit der Querschnittsflächen vom Winkel α
1
0 0
α
b) α = 30°–Gitterrost
2
3
40°
50°
15° 30° 45° 60° 75° 90°
f 2
f 1
f 1
Zusätzliche Aussteifung
Bild 6.7 : Querschnittsflächen im Scheiben–Gitterrost
α
1
c) α = 60°–Gitterrost
2
3
Lagerung
0
0
α
f 3
f 3
f 2
f 2
α
A0 � 3
at ,
16
A 1 � f 1 A 0 ,
A 2 � f 2 A 0 ,
A 3 � f 3 A 0 .
f 1
t
a

6.2.3 Scheibenbeispiel Kragarm: Verschiebungen
Die vorgestellte Möglichkeit, Scheibenprobleme mit Hilfe der Fachwerkanalogie zu
lösen, soll nun an einem einfachen Beispiel erprobt werden. Es handelt sich um ein
Kragarm–Beispiel, so daß bei einem analytischen Lösungsversuch die Erfüllung der
geometrischen Randbedingungen erhebliche Schwierigkeiten bereitet. Das System
und die Unterteilung in Fachwerkstäbe sind im (Bild 6.8) dargestellt.
L 2 = 10.
a) System und Belastung
5.
a
a
a
X 2 , u 2
Eingespannter Rand:
X 1 , u 1
Freier Rand
Fall 1 mit u1(X 1 = 0, X 2 ) = 0
und u2(X 1 = 0, X 2 = 0) = 0.
Fall 2 mit u1(X 1 = 0, X 2 ) = 0
und u2(X 1 = 0, X 2 ) = 0.
E = 3⋅10 7 , ν = 0.33, t = 0.20
Freier Rand
L 1 = 10.
b b b b b b
10.
– 6 / 18 –
Q = 1000.
a � b � 10
6
α = 45°
� 1.666
Symmetrielinie X 2 = 0.
b) Unterteilung des halben Systems in 18 Gitterrostelemente mit 81 Fachwerkstäben
Bild 6.8 : Berechnungsbeispiel Kragarm
Aus Symmetriegründen reicht es aus, nur das halbe System zu betrachten. Die Untersuchung
wird mit 21 vertikalen, 24 horizontalen und 36 diagonalen Stäben und zwei
unterschiedlichen Randbedingungen für den eingespannten Rand duchgeführt:
– Im ersten Fall ist der Rand zwängungsfrei in Richtung der X 2 –Koordinate gelagert,
so daß sich auch in der Lagerung eine ungestörte parabolische Spannungsverteilung
der Schubkräfte einstellen kann.

– Im zweiten Fall ist der Rand vollständig eingespannt, so daß es durch die Zwängung
zu einer Störung in der Verteilung der Schubspannungen kommt.
Die Neigung der Diagonalen beträgt α = 45°. Für ein Gitterrost ergeben sich damit die
Querschnittsflächen
A 0 � 0.0625 ,
A 1 � A 0 ⋅f 1 � 0.0625⋅2.0 � 0.125 ,
A 2 � A 0 ⋅f 2 � 0.0625⋅2.0 � 0.125 ,
A3 � A0⋅f3 � 0.0625⋅2.0⋅ 2 � � 0.17677670 .
Im Fachwerkmodell sind die Stabflächen der vertikalen und horizontalen Kontaktstäbe
unmittelbar benachbarter Gitterrostelemente zu addieren.
Die resultierende Einwirkung Q wird parabolisch über die Höhe verteilt und danach zu
resultierenden Knotenlasten zusammengefaßt, um sie den Fachwerkknoten anteilig
einprägen zu können.
Die Berechnung wird mit dem FEMAS–Programm des Fachgebiets Statik der Bau–
konstruktionen durchgeführt, das auf der Methode der Stabsteifigkeiten beruht /12/. Im
(Bild 6.9) sind die Elemente und Knoten dargestellt und im (Bild 6.10) die resultierenden
Verschiebungen für Fall 1 und Fall 2.
Der Fall 1 mit ungezwängtem Rand sollte zumindest hinsichtlich der Lagerung mit der
Balkentheorie vergleichbar sein, da die Krafteinleitung wie am freien Ende ebenfalls zu
einer quadratischen Verteilung führen muß, da keine Behinderung vorliegt. Für den
schubstarren Biegebalken errechnet sich die Durchbiegung am Kragarmende zu
f Biegung � Q(L 1 )3
3EI
1000⋅103
�
3⋅3⋅107 0.20⋅103 �
12
20
3 ⋅10�4 � 0.666⋅10�4 .
Wird zusätzlich der Einfluß der Schubverformung berücksichtigt, erhöht sich die Durchbiegung
um den Wert
Q⋅L1 fSchub � �Q GA
� 1.2
1000⋅10
3⋅10 7
2�1�0.33� 0.20⋅10 � 2⋅2.6⋅10�4 � 5.2⋅10 �4 .
Die maximale Durchbiegung nach der Balkentheorie errechnet sich demnach zu
fmax � f Biegung � f Schub � 1.18666⋅10 �3 .
Nach (Bild 6.10a) ergibt sich der Vergleichswert der Scheibenlösung zu
fmax � 1.301⋅10 �3 .
– 6 / 19 –

Die Scheibe verhält sich also um 8.8 % nachgiebiger als der Balken, wenn keine Randzwängung
vorliegt (Bild 6.8, Fall 1).
Im Fall 2 wird die Scheibe durch den gezwängten Rand steifer. Die Durchbiegung
nimmt ab und erreicht nach (Bild 6.10b) den Wert
fmax � 1.119⋅10 �3 .
Die Abweichung zur Balkenlösung beträgt 5.7 %. Um dieses Maß ist die Scheibe steifer
als der Balken, wenn eine Randzwängung vorliegt (Bild 6.8, Fall 2).
Der Verformungsvergleich zeigt, daß zwischen der Scheiben– und Balkenlösung nur
geringe Unterschiede bestehen, wenn die Balkentheorie zusätzlich den Schubeinfluß
enthält. Dieses Ergebnis darf aber nicht überbewertet werden, da es nicht immer so sein
muß. Das Verformungsverhalten von Scheiben hängt neben der Systemgeometrie und
Belastung vor allem von den vorliegenden Randbedingungen ab, die im Fall des
Kragarmbeispiels bereits optimal von der Balkentheorie erfaßt werden. Bei anderen
Verhältnissen ist daher durchaus mit größeren Abweichungen zwischen Scheiben– und
Balkenlösungen zu rechnen.
X 2
a) Elemente
X 2
19 20 21 22 23 24
76 77 78 79 80 81
39
58
13
40
59
14
41
60
15
42
61
16
43
62
44
63
17 18
70 71 72 73 74 75
32
52
33
53
34
54
35
55
36
56
37
57
7 8 9 10 11 12
64 65 66 67 68 69
25
46
26
47
27
48
28
49
29
50
30
51
X1 1 2 3 4 5 6
Elementnummern
22 23 24 25 26 27 28
15 16 17 18 19 20 21
8 9 10 11 12 13 14
1 2 3 4 5 6 7
X 1
b) Knoten
Bild 6.9 : Scheibenbeispiel Kragarm
Knotennummern
– 6 / 20 –
45
38
31

a) Fall 1 : Ohne Randzwängung
b) Fall 2 : Mit Randzwängung
Bild 6.10 : Scheibenbeispiel Kragarm. Verschiebungsfigur
– 6 / 21 –

6.2.4 Ermittlung der Scheibenkräfte
Ein unmittelbarer Vergleich zwischen den Stabkräften des Fachwerks und den Längs–
und Schubkräften der Scheibe ist nicht möglich, da es sich bei den Stabkräften um
punktbezogene und bei den Scheibenkräften um längenbezogene Größen handelt. Vor
dem Vergleich ist also eine zusätzliche Umrechnung erforderlich. Es stellt sich daher
die Frage, ob es nicht sinnvoller ist, die Bemessung der Scheibe direkt mit den Stabkräften
des Fachwerks vorzunehmen, wenn zuvor die Einflußlängen der Stabkräfte abgeschätzt
werden. Um dies entscheiden zu können, müssen die Umrechnungsbeziehungen
zwischen Scheiben– und Fachwerkskräften bekannt sein. Dazu sind lediglich die
Gl. (6.7, 6.10 und 6.15) nach den Scheibenkräften aufzulösen. Wird Gl. (6.7 und 6.15)
in Gl. (6.10) eingesetzt und die Zwangsbedingung ν = 1/3 beachtet, folgt die Bestimmungsgleichung
der Scheibenkräfte zu
�4cos 2 ϕn � 1�n 11
� �4sin 2 ϕn � 1�n 22
� (8sinϕncosϕn )n12 � 16
�Nn a�
f
mit n � 1, 2, 3 .
– 6 / 22 –
(6.18)
Die Auswertung der Verträglichkeitsbeziehung (6.18) ist knotenweise durchzuführen.
Die Zuordnung zwischen Scheiben– und Stabkräften ist (Bild 6.11) zu entnehmen.
n 11
D
A
n 12
Bild 6.11 : Scheiben– und Stabkräfte
�
�
N 3
N 1
2
α α
ϕ
1 1
N1 N3 N 2
N 2
n 22
n 21 = n 12
3 3
n 21 = n 12
2 N 2
n 22
b = a tanα
N 2
N 3
N 1
N 1
N 3
�
�
n 12
C
B
n 11
a

Die Neigungswinkel der Stäbe im Gitterrost betragen an den Knoten A und C
ϕ1 � 90°, ϕ2 � 0° und ϕ3�90° � �
und an den Knoten B und D
ϕ1 � 90°, ϕ2 � 0° und ϕ3�90° � � .
Damit sind die Vorfaktoren von n 11 und n 22 für alle Knoten gleich, während sie sich
bei n 12 durch den Richtungswechsel der Diagonalen unterscheiden.
sin� � cos(90° � �) ��cos(90° � �) ,
cos� � sin(90° � �) � sin(90° � �) .
Winkel Diagonale AC
Winkel Diagonale BD
Die explizite Form von Gl. (6.18) ergibt sich damit zu
mit
und
n 11 n 22 n 12 Rechte Seite
–1 3
4sin 2 � � 1
– 6 / 23 –
16
3 –1
16
f 1 � 3tan� � cot� ,
f 2 � 3 � tan 2 �
f 3 �
1
sin�cos 2 �
4cos 2 � � 1 � 8sin� cos�
16
�N1 a�
als Einflußfaktoren der Stabflächen, vgl. Gl. (6.16.2 bis 6.16.4).
f 1
� N 2
a�
f 2
� N 3
a�
f 3
(6.19.1)
(6.19.2)
(6.19.3)

Die Auflösung von Gl. (6.19) nach den Scheibenkräften ergibt:
und
mit
n 11 �
n 22 �
3� N 2
L �
f 2
3� N 1
L �
f 1
�
�
� N 1
L �
f 1
� N 2
L �
f 2
n12 ���cos��N3� �
1
L
L � a
2
,
8 �3
f2 f1tan� � 1��N 1
L
– 6 / 24 –
(6.20.1)
(6.20.2)
� �
1
8�3 f1 � 1
tan���N2�� (6.20.3)
L
. (6.20.4)
Anmerkung zur Bestimmung von n 12 :
Es ist
und
4sin2� � 1
8sin�cos� � 3sin2� � cos2� 8sin�cos�
4cos2� � 1
8sin�cos� � 3cos2� � sin2� 8sin�cos�
1
�
8sin�cos� f3 sin�cos2� 8sin�cos�
�
1�
sin�
8 cos�
�
cos�
sin�� � �1 8 3tan� � cot�� � 1
8 f1 ,
� 1
8
�
1
cos� .
8
�3 cos�
sin�
Damit wird n12 ��� N3�cos� �
1
L 8 f1n11 � 1
8 f2 f 2
�
sin��
cos�
�
1
8 �3 � tan2�� 1
�
1
tan� 8 f2 1
tan�
1
tan� n22 usw.
Bei der Auflösung von Gl. (6.19.3) ist die Vorzeichenregel von n 12 zu beachten. Für
die Knoten A und C ist n 12 positiv und für die Knoten B und D negativ. Mit Gl. (6.20)
sind die Längs– und Schubkräfte der Scheibe für ein Gitterrost eindeutig bestimmt. Bei
rechteckigen Gitterrosten treffen maximal vier Gitterrostelemente in einem Knoten zu–
sammen. Die Scheibenkräfte nach Gl. (6.20) werden zunächst für die einzelnen
Elemente getrennt berechnet. In der Regel fallen diese Werte unterschiedlich aus,
da es sich um ein Näherungsverfahren handelt. Es ist daher sinnvoll, die endgültigen

Knotenwerte durch eine arithmetische Mittlung der Einzelbeiträge zu bestimmen. Dies
ist im (Bild 6.12) veranschaulicht.
Element
Element
2
3
α 2
α 3
b1 = tanα2a1 = tanα3a2
Bild 6.12 : Mittlung der Scheibenkräfte
B
C
(SK)
– 6 / 25 –
�
A
D
α 1
Element
α 4
Element
b2 = tanα1a1 = tanα4a2
Im betrachteten Systemknoten (SK) treffen die Knoten A des ersten, B des zweiten,
C des dritten und D des vierten Elements zusammen. Die resultierenden Kräfte in den
Kontaktstäben unmittelbar benachbarter Elemente müssen zunächst im Verhältnis der
Anteile der Stabflächen auf die einzelnen Elemente verteilt werden. Zwischen den Elementen
1 und 2 gilt z.B.
Element 2
Element
2
N1 N 1
� � �
B (SK) A
1 2
A1 � A1 � A1 1
N1 1
1
4
1
N1 und
2
N1 � N 1
1
A1 A1 2
A1 � N1 A1 a 1
a 2

Die Fläche A 1 ist die Summe der Querschnittsflächen aller beteiligten Elemente und
N 1 die daraus resultierende Stabkraft, die aus der Fachwerkberechnung folgt. Sind alle
Stabkräfte in den Elementen bekannt, können mit Gl. (6.20) die zugehörigen Scheibenkräfte
berechnet und anschließend die knotenweise Mittlung vorgenommen werden.
Für n 11 gilt z.B.
n11 n
2
11
,B 1 ,A
n 11
3
�
B
(SK) �
�
A
C D
� �
n 11
n11 ,C 4 ,D
– 6 / 26 –
(SK) � n11 ,A � n11 ,B � n11 ,C � n11 1 2 3 4 ,D
.
4
Um nun die eingangs gestellte Frage zu beantworten, ob die Bemessung der Stäbe direkt
mit den Stabgrößen des Fachwerks erfolgen kann, werden für die Stabkräfte Einflußlängen
definiert, die sich unmittelbar aus Gl. (6.20) ergeben. Es gilt:
mit
n11 � N1 �
L11,1 N2 L11,2 n22 � N1 �
L22,1 N2 L22,2 n12 � N1 �
L12,1 N2 �
L12,2 N3 L12,3 , (6.21.1)
, (6.21.2)
(6.21.3)
L11,1 � f1L, L11,2 � (6.22.1)
1
3 f2L, L22,1 � 1
3 f1L, (6.22.2)
L22,2 � f2L, L 12,1 ��
�3 f 2
f 1 tan�
8L
, (6.22.3)
� 1� L12,2 ��
8L
�3 f1 � 1
tan�� , L12,3 �
1
cos� L.
f 2

Die Zusammenhänge zwischen den Einflußlängen und den Scheibenkräften lassen
sich in einfacher Weise anhand eines quadratischen Gitterrostes mit α = 45° diskutieren.
Es ist f1 � f2 � 2, cos� � 2 � �2 und tan� � 1, so daß sich die Einflußlängen
aus Gl. (6.20.4 und 6.22) zu
und
L 11,1 � a, L 11,2 � a
3 ,
L22,1 � a
3 , L22,2 � a,
L 12,1 ��a, L 12,2 ��a
L12,3 � 2 � �a 2 �
errechnen. Mit Gl. (6.22) sind dann auch die Scheibenkräfte bekannt, die sich aus
und
n11 � N1 a � N2 a
3
n 12 ��� �
� � N 1
a � N 2
,n 22 � N 1
a
3
a � N3 2
� N 2
a
� �a 2��� � �� � N1 � N2 a
– 6 / 27 –
� 2 � N3 ergeben. Bei n 11 ist die erste und bei n 22 der zweite Term auf den Einfluß von ν = 1/3
zurückzuführen, da L 11,1 das Dreifache von L 11,2 bzw. L 22,2 von L 22,1 ist. Dies
ist im (Bild 6.13) veranschaulicht. Die quer zur Scheibenlängskraft n 11 verlaufende
Stabkraft N 1 liefert gerade den ν–fachen Anteil von N 1 (Bild 6.13a) und die quer
zur Scheibenlängskraft n 22 verlaufende Stabkraft N 2 gerade den ν–fachen Anteil
von N 2 (Bild 6.13b) als Beitrag zu den Scheibenkräften.

N 1
N 1
a) Längskraft n 11
N 2
N 2
a
3
a
3
n 11
b) Längskraft n 22
a
3
a
3
a
3
a
3
n22 � 1
3
n 22
Bild 6.13 : Einfluß der Querdehnzahl
N 1
N 1
N 2
n11 � 1
3
�a 3� � N2 a
– 6 / 28 –
a
3
a
3
Der Querzug aus der Stabkraft N 1
erzeugt eine Scheibenlängskraft n 11 ,
da ν = 1/3 gilt !
N 1
�a 3� � N1 a
N 2
N 2
Der Querzug aus der
Stabkraft N 2 erzeugt
eine Scheibenlängs–
kraft n 22 , da ν = 1/3 gilt !
Die Hauptanteile der Scheibenkräfte n 11 und n 22 ergeben sich durch die Verteilung
von N 2 und N 1 auf die Einflußlängen L 11,2 = L 22,1 = a/3. Dies ist im (Bild 6.14) ver–
anschaulicht. Für n 11 gilt das Verteilungsschema (Bild 6.14a) und für n 22 das Verteilungsschema
(Bild 6.14b).

n 11
a
3
a) Scheibenlängskraft n 11
b) Scheibenlängskraft n 22
a
3 N2 A B
b = a
a
D
D
Bild 6.14 : Verteilung der Stabkräfte in Längsrichtung
a
3
N 1
N 2
n 22 � N 1
� a
3 �
a
3
N 1
C
A a a B
3 3
n 22
C
– 6 / 29 –
a
3
a
3
n 11 � N 2
� a
3 �
Die Verteilungslänge von a/3 resultiert aus der Forderung nach statischer und geo–
metrischer Äquivalenz, die von einer gleichwertigen Erfüllung von Gleichgewicht und
Verträglichkeit im Scheiben– und Fachwerkmodell ausgeht. Wird auf die Erfüllung der
elastischen Verträglichkeit verzichtet, können die Scheibenkräfte unmittelbar aus den
globalen und lokalen Gleichgewichtsbedingungen Gl. (6.1 und 6.2) ermittelt werden,
wenn die Aufteilung zwischen Längs– und Schubkräften in einem bestimmten Verhält-

nis folgt, d.h., wenn z.B. die Längskräfte den horizontalen und vertikalen Fachwerk–
stäben und die Schubkräfte den Diagonalen zugeordnet werden. Im Knoten A gilt z.B.
und
Dann ist
und
Gl. (6.1) Gl. (6.2)
1
2 a�n 11 � tan�n 12� � N 2 � N 3 sin�
1
2 a�tan�n 22 � n 12� � N 1 � N 3 cos�
– 6 / 30 –
� N 1 A
� N 2 A
Global: Scheibe Lokal: Fachwerk Knotenkräfte
n 11 � tan�n 12 � 2 �N 2 � N 3 sin��
a
tan�n 22 � n 12 � 2 �N 1 � N 3 cos��
a
(6.23.1)
. (6.23.2)
Die gleichwertige Aufteilung auf Längs– und Schubkräfte führt mit α = 45° auf die
Längskräfte
n 11 � N 2
� a
2 �
und n22 � N1 .
�
� a
2
Demnach fehlt bei dieser speziellen Gleichgewichtsverteilung der Einfluß der Querdehnzahl.
Zusätzlich wachsen auch die Verteilungslängen um 50% an. Daher fallen
die Maximalwerte der Scheibenlängskräfte insgesamt kleiner als bei einer elastisch verträglichen
Verteilung aus, ein Ergebnis, das mit der Erfahrung im Einklang steht.
Bei der Schubkraft sind die Verhältnisse nicht ganz so einfach zu übersehen. Bei vollständiger
Äquivalenz zwischen Scheiben– und Fachwerkmodell verteilen sich die
Diagonalkräfte auf die halbe Diagonallänge und die abmindernd wirkenden horizontalen
und vertikalen Stabkräfte auf die volle Seitenlänge. Das Verteilungsschema ist im
(Bild 6.15) dargestellt.

a
�2 a
2
�2 a
2
D
N 1
N 1
N 3
N 2
n 21 = n 12
A n B
21 = n12 Bild 6.15 : Ermittlung der Schubkräfte n 12 und n 21 , α = 45°
a
�
– 6 / 31 –
N 2
n 12 n 12
N 3
N 2
a
N 3
N 3
N 2
C
N 1
N 1
�2 a
2
�2 a
2
Die Begrenzung der Breite zur Verteilung der Diagonalkräfte steht mit der Erfahrung
im Einklang. Für die Kraft zwischen A und C sind die Ecken B und D und für die
Kraft zwischen B und D die Ecken A und C ’tote’ Spannungsecken, da sich der Spannungsfluß
vor allem in Richtung der Diagonalen ausbreitet und die abgelegenen Ecken
nicht erreicht. Die Umformung von
in
n 12 ��� �
� � N 1
a � N 2
n 12 �� � �
a � N3 2
� 1 a�� N 1 � 2
�
� �a 2��� �
2 N3� � 1 a�� N2 � 2 �
2 N3�� �
�
a

zeigt, daß keine Schubkräfte auftreten, wenn die Ausdrücke in runden Klammern identisch
verschwinden. Dann gilt z.B. im Knoten A
n 12
N 1
�
�2
2 N3 �2
2 N3 N 2
N 3
� N1 � 2 �
2 N3 � 0
und
� N2 � 2 �
2 N3 � 0.
Die vertikalen und horizontalen Komponenten der Diagonalkräfte und die Kräfte der vertikalen
und horizontalen Stäbe heben sich gegenseitig auf, so daß es nicht zu einer
Schiefstellung des Gitterrostelements kommen kann und im äquivalenten Scheiben–
modell keine Schubdehnungen und damit auch keine Schubkräfte auftreten.
Die spezielle Gleichgewichtsverteilung mit gleichwertiger Behandlung der Längs– und
Schubkräfte führt dagegen auf die Schubkräfte
n12 �� N3 �2 �a .
�
2
Die Verteilungslängen der dominanten Diagonalkräfte sind also gleich, während der abmindernde
Einfluß der horizontalen und vertikalen Stabkräfte vollständig entfällt. Bei
diesem Gleichgewichtsmodell sind die Schubkräfte demnach größer als beim Verträglichkeitsmodell
und kompensieren damit den Abfall der Längskräfte.
Da die Wertigkeit von Längs– und Schubkräften in Gleichgewichtsmodellen von außen
vorgegeben wird, sind weitere Varianten denkbar. Ein gängiges Modell ist z.B. die Aufteilung
über die Knotenkräfte nach Gl. (6.1). Im Knoten A (Bild 6.16) gilt z.B.
und
1
2 a�n 11 � tan�n 12� � N 1
A
1
2 a�tan�n 22 � n 12� � N 2
A .
– 6 / 32 –

n 11
N 1 A
n 12
A
N 2 A
�
1
b �
1
2 2 atan�
α
n 12
n 22
1
2 a
1
2 a
Bild 6.16 : Alternative Verteilung der Stabkräfte im Knoten A
Die Verteilung auf die anliegenden Seitenlängen führt auf die Längs– und Schubkräfte
und
n11 � N1 A
, (6.24.1)
�
� a
2
n 22 � N2 A
�tan� a
2 �
n 12 �
N 2
A
� a
2
N1
A
�
�
– 6 / 33 –
(6.24.2)
�tan� a
2� . (6.24.3)
2
Die Knotenkräfte mit Hilfe von Gl. (6.2) durch die Stabkräfte ausgedrückt, ergibt
und
n11 � N2 �a 2� � sin� N3 �a 2
n 22 � N 1
tan�� a
n 12 �
� ,
2� � cos� N3 tan��a 2� N1 �a 2� � N2 tan��a 2� � 2cos� N3 �a 2� 2
.

Mit α = 45° folgt daraus
und
n 11 � N 2
n 22 � N 1
n 12 �
2
� �
2 N3 �a 2� 2
� �
2 N3 �a 2� N1 2 � N2 2
,
2
� �
2 N3 � a
2 �
,
also eine Verteilung, die von der elastisch verträglichen Verteilung nach Gl. (6.20 bzw.
6.21) nicht unerheblich abweicht und die sich auch deutlich vom ersten Gleichgewichtsmodell
unterscheidet, das auf einer gleichwertigen Aufteilung der Längs– und Schubkräfte
in Gl. (6.23) beruht.
Trotz der Unverträglichkeiten, die aus der Verletzung der elastischen Verträglichkeit
folgen, ist die reine Gleichgewichtsverteilung der Stabkräfte im Hinblick auf die praktische
Anwendung besonders attraktiv. Sie erlaubt nämlich die unmittelbare Bemessung
der Scheibe mit den Stabkräften des Fachwerks, wenn man dabei das erste der diskutierten
Gleichgewichtsmodelle in vereinfachter Form einsetzt.
Am Fachwerk, das aus zusammengesetzten Gitterrosten besteht, kann z.B. nach dem
Schema in den (Bildern 6.17 bis 6.19) verfahren werden, um die Scheibenkräfte zu
ermitteln. Im (Bild 6.17) ist die vereinfachte Ermittlung der Scheibenkräfte n 11 veranschaulicht,
im (Bild 6.18) die vereinfachte Ermittlung der Scheibenlängskraft n 22 und
im (Bild 6.19) die vereinfachte Ermittlung der Scheibenschubkräfte n 12 = n 21 .
– 6 / 34 –

a 1
a 2
X 2
Gitterrost
� �
N h
� �
Gitterrost
1
2
L h
X 1
– 6 / 35 –
N h = Resultierende Kraft
der horizontalen Stäbe.
L h =
n 11 � N h
L h
Bild 6.17 : Vereinfachte Ermittlung der Scheibenlängskraft n 11
�a 1 � a 2 �
.
3
Zugehörige horizontale
Verteilungslänge.
(6.25.1)
Im (Bild 6.17) ist N h die resultierende Kraft der horizontalen Stäbe. Sie ist unmittelbar
durch die Fachwerkberechnung bekannt. Für quadratische Gitterroste mit α = 45° gilt
für die Gitterroste 1 und 2
und
1
N 2 � N h
1
2
N 2
1
A 2 +
N 2 � � N h .
1
A 2
2
A 2
und
2
N 2 � N h
1
A 2 +
2
A 2
2
A 2
Die zugehörige horizontale Verteilungslänge wird aus dem Verträglichkeitsmodell übernommen
und berechnet sich zu
L h � �a 1 � a 2 �
3
.
In gleicher Weise ist in den (Bildern 6.18 und 6.19) zu verfahren.

�
�
X 2
Gitterrost
b 1
Nv
1
L v
n 22 � Nv
Lv
�
�
Gitterrost
b 2
2
– 6 / 36 –
N v = Resultierende Kraft
der vertikalen Stäbe.
L v =
X 1
�b 1 � b 2 �
Bild 6.18 : Vereinfachte Ermittlung der Scheibenlängskraft n 22
X 2
a
n 12 � � N d
L d
N d
L d
=
=
L d Ld
�
�
�2 a
2 .
N d
Kraft der Diagonalstäbe.
�
�
.
3
Zugehörige vertikale
Verteilungslänge.
n 12 � N d
L d
Bild 6.19 : Vereinfachte Ermittlung der Scheibenschubkräfte n 12 = n 21
X 1
Zugehörige diagonale Verteilungslänge.
(6.25.1)
(6.25.3)

6.2.5 Scheibenbeispiel Kragarm: Spannungen
Am Beispiel des bereits unter Pkt. 6.2.3 behandelten Kragarms sollen die unter
Pkt. 6.2.4 diskutierten Möglichkeiten der Spannungsauswertung erprobt werden. Da
die Spannungen und Kräfte der Scheibe nur über die Dicke zusammenhängen, reicht
es aus, die Längs– und Schubkräfte zu bestimmen. Die Auswertung erfolgt in den
Schnitten X 1 = 0.0, X 1 = 5.0 und X 1 = 10.0, also in der Einspannung, der Mitte und am
freien Rand, vgl. (Bild 6.8). Für die Kräfteauswertung wird lediglich der Fall 2 mit voller
Einspannung betrachtet, da dieser Fall die wirklichen Randbedingungen der Kragscheibe
realistischer als der Fall 1 erfaßt. Die zwangsfreie Lagerung in X 2 –Richtung
ist dagegen von Interesse, wenn es darum geht, das Durchbiegeverhalten der Scheibe
mit Mitteln der Balkenstatik zu überprüfen. Es wird zusätzlich eine numerische Scheibenlösung
als Vergleichslösung herangezogen, um die Lösung nach der Fachwerkanalogie
bewerten zu können. Sie wird mit dem FE–Programm HYDAS des Fachgebiets
Statik der Baukonstruktionen ermittelt, in dem ausschließlich Weggrößenelemente implementiert
sind /13/. Teilergebnisse sind zahlenmäßig in (Tabelle 6.1) angegeben und
grafisch im (Bild 6.24) dargestellt.
Die Durchführung der Berechnung nach dem Verträglichkeitsmodell Gl. (6.20) wird
exemplarisch im Schnitt X 1 = 5.0 am Knotenpunkt X 2 = 3.3333 erläutert (Bild 6.21).
An dieser Stelle stoßen vier Gitterrostelemente zusammen. Die Längs– und Schubkräfte
n 11 und n 12 sind zunächst für die einzelnen Elemente zu bestimmen und danach
am Knotenpunkt zu mitteln, der im (Bild 6.9b) die Nummer 18 erhalten hat.
Gitterrostelement 2
281.6
2
281.6
2
139.7
N 2
N 2
–80.5
� 100
2
N 3
n 12
N 1
n 12
n 12
Gitterrostelement 3
n 11
Bild 6.21 : Knotenpunkt im Fachwerk
B
18
– 6 / 37 –
Gitterrostelement 1
n 11
� 100
2
N 1
n 12
A
N 3
n 12
n12 n12 C D
N 3
N 1
� 58.5
2
n 11
n 11
n 12
N 1
� 58.5
2
N 3
5.3
N 2
N 2
201.6
2
X 2 = 3.333
201.6
2
167.0
Gitterrostelement 4

Aus der Fachwerkberechnung sind die Stabkräfte bekannt, die sich entsprechend den
Flächenanteilen auf die einzelnen Gitterrostelemente verteilen (Bild 6.21). Für die vertikalen
und horizontalen Stäbe beträgt der Verteilungsfaktor Zwei und für die Diagonalstäbe
Eins. Für ein Gitterrostelement gilt
und
Mit 1 a � 1 10
6
n 11 � 1 a �N 1 � 3N 2 �
n12 �� 1 a�� N1 � N2 � 2 � N � 3
� 6
� 0.6 folgt daraus
10
im 1. Gitterrostelement
n11 � �� 100
� 3
201.6
2 2 �0.6 � 151.4 ,
n 12 � � 100
2
� 201.6
2
im 2. Gitterrostelement
– 6 / 38 –
+ für AC
– für DB
� 2 � ⋅5.3�0.6 ��26.0 ,
n11 � �� 100
� 3
281.6
2 2 �0.6 � 223.4 ,
n 12 ��� 100
2
im 3. Gitterrostelement
n11 � �� 58.5
2
n 12 � � 58.5
2
� 281.6
2
� 2 � ⋅139.7�0.6 ��64.1 ,
� 3
281.6
2 �0.6 � 235.9 ,
� 281.6
2
und im 4. Gitterrostelement
n11 � �� 58.5
2
n 12 ��� 58.5
2
� 2 � ⋅80.5�0.6 ��135.2 ,
� 3
201.6
2 �0.6 � 163.9 ,
� 201.6
2
� 2 � ⋅167.�0.6 ��98.8 .
Die arithmetische Mittlung der Einzelergebnisse führt mit
n11 � �151.4 � 223.4 � 235.9 � 163.9�
� 193.7
4
.

und
n12 ���26.0 � 64.1 � 135.2 � 98.8�
��81.0
4
auf Werte, die nur wenig von den Vergleichswerten der Finite–Element–Berechnung
abweichen, vgl. (Tabelle 6.1).
Die direkte Verteilung der Stabkräfte des Fachwerks nach Gl. (6.25) ist für die Scheibenlängskraft
n 11 im (Bild 6.22) dargestellt.
18
281.6 201.6 2a
�
1
3 0.9
n11 � 1 (281.6 � 201.6)0.9 � 217.4
2
Bild 6.22 : Vereinfachte Ermittlung der Scheibenlängskräfte n 11
Die direkte Verteilung der Schubkraft n 12 = n 21 ist (Bild 6.23) zu entnehmen.
–
�2 ⋅
a
2
n
–
12 �� 2 � �
n
+
12 � 2 � �
n 12 � – n +
12 � n 12
2
139.7 5.3
Bild 6.23 : Vereinfachte Ermittlung der Schublängskraft n 12 = n 21
18
�
–80.5 167.
– 6 / 39 –
�2 ⋅
a
2
�
1
0.6 2 �
139.7 � 167. �0.6 ��130.1
2
5.3 � 80.5�0.6
��31.9
2
��81.0
n 11
+
n 12

Die Werte von Gl. (6.25) liegen ebenfalls in der Größenordnung der Finite–Element–
Lösung. Dies trifft i.a. auch für die Gleichgewichtsmodelle nach Gl. (6.23 und 6.24) zu.
Für die praktische Anwendung der Gitterrostmethode zur Lösung von Scheibenauf–
gaben ist es daher am einfachsten und völlig ausreichend, die Verteilungslängen der
Stabkräfte abzuschätzen und die Scheibenkräfte unmittelbar am Fachwerkmodell zu
bestimmen.
Der im (Bild 6.24) dargestellte Verlauf der Längs– und Schubkräfte zeigt einen deut–
lichen Scheibeneffekt, der sich besonders in der Einspannung X 1 = 0 bemerkbar
macht. Erst wenn die L 2–Länge im Verhältnis zur L 1–Länge stark abnimmt, wird sich
eine gradlinige Verteilung der Spannungswerte in X 2 –Richtung einstellen und die Balkenlösung
dominieren.
Koor–
dina–
te
X 2
0.
X 1
0.
n 11
1.666 139.3
3.333
5.000
Koor–
dina–
te
X 2
0.
X 1
1.666
3.333
5.000
0.0
317.3
667.1
0.
n 11
Tabelle 6.1 :
Verträglichkeits
modell Gl. (6.20)
n 11 n 12 n 12
–5.6 –144.2 –143.1 0.0 –145.0 –76.0 –147.2
83.4 –129.0 92.8 –127.9 137.9 –129.4
295.2
217.4
5. 10.
5. 10.
n 11 n 12 n 12
0. 5. 10. 0. 5. 10.
n 11 n 11 n 12 n 12
–52.5 444.7
–38.8 686.9 –25.0
n11 n11 n12 n12 0.
Vergleichslösung mit
finiten Elementen
5. 10.
816.2
Gleichgewichts–
modell Gl. (6.23)
– 6 / 40 –
–141.0
n 11 n 11 n 12 n 12
193.6 –81.0 –82.1 –211.5 –79.8 315.8
–77.2
Direkte Verteilung
am Fachwerk Gl. (6.25)
–81.0
0.0
160.2
290.2
–3.1
104.5
191.4
305.6
–142.8
–73.7
–5.3
Längs– und Schubkräfte einer Kragscheibe.
Vergleich unterschiedlicher Lösungsmodelle
–151.5
–146.2
–90.5
–12.4
Gleichgewichts–
modell Gl. (6.24)

5.0
3.333
1.666
X 2
–100 0. 100 200 300 400 500 600 700 800 900
a) Schnitt X 1 = 0. : Einspannung
5.0
3.333
1.666
X 2
–100 0. 100 200 300
b) Schnitt X 1 = 5.0 : Mitte
n 11
FE–Programm HYDAS /13/
Gitterrost–Lösung
Verträglichkeitsmodell
Gitterrost–Lösung
Direkte Verteilung am Fachwerk
c) Schnitt X 1 = 10. : Freier Rand
Bild 6.24 : Scheibenbeispiel Kragarm. Vergleich der Spannungswerte
– 6 / 41 –
–200
–200
X 2
5.0
3.333
1.666
n 22
n 12
–100 0. 100 200 300
X 2
5.0
3.333
1.666
–100 0. 100 200 300
n 11
n 11
n 12
n 12

6.2.6 Stab– Querschnittsflächen für beliebige Querdehnzahlen
Die Ersatzflächen der Gitterroststäbe Gl. (6.15) gelten nur für den Sonderfall ν = 1/3.
Weicht die Querdehnzahl eines realen Werkstoffs von diesem Wert ab, so ist die Analogie
zwischen Scheibe und Fachwerk als mehr oder weniger gute Näherung anzusehen.
Für Stahl z.B. beträgt die Querdehnzahl ν = 0.3. Die Abweichung zum Sollwert von
Gl. (6.15) ist sehr gering, so daß immer mit Gl. (6.15) gerechnet werden darf, ohne einen
größeren Fehler zu begehen. Bei Stahlbeton mit ν = 1/6 oder ggf. anderen Werkstoffen
ist zwar mit einer größeren Abweichung zu rechnen. Für die praktische Anwendung ist
aber Gl. (6.15) immer noch als ausreichend genau anzusehen.
Trotzdem sollen nun noch die Stabflächen für veränderliche Querdehnzahlen ermittelt
werden. Vor allem, um abschätzen zu können, wie stark sie den Wert der Stabflächen
beeinflussen. Für das bislang betrachtete rechteckige Gitterrost ist dies in einfacher
Weise möglich, wenn die Anzahl der Knoten im Gitterrost erhalten bleibt und lediglich
die Anzahl der Stäbe zwischen den Knoten erhöht wird, um die Eindeutigkeit der Lösung
zu gewährleisten.
Es sind also zusätzlich Stäbe im Gitterrost anzuordnen, damit keine Überbestimmung
in Gl. (6.14) für ν ≠ 1/3 auftritt. Eine eindeutige Zuordnung ergibt sich, wenn man die
Einheitsverformungszustände �K �� der Scheibendehnung und Scheibengleitung im
(Bild 6.25) getrennt betrachtet.
A 2
A 3
a) Scheibendehnung � K 11
A 3
α
n 21
c) Scheibengleitung � K 12
n 12
n 11
Bild 6.25 : Einheitsverformungszustände
– 6 / 42 –
t
A 3
X 2
n 22
A 1
b) Scheibendehnung � K 22
a
X 1

Die Einheitszustände �K 11 , �K 22 und �K 12 sollen der Reihe nach sowohl am Scheibenkontinuum
als auch am Gitterrost wirken. Die Analogie zwischen Fachwerk und Scheibe
führte für �K 11
und für � K 22
auf Gl. (6.14.1)
A 2 � A 3 sin 3 � �
Fachwerk und Gl. (6.14.2)
A 3 sin 2 �cos� �
auf Gl. (6.14.3)
A 3 cos 2 �sin� �
Fachwerk und Gl. (6.14.4)
A 1 � A 3 cos 3 � �
at
2�1 � � 2�
at tan��
2�1 � � 2�
at�
2�1 � � 2�
at tan�
2�1 � � 2�
– 6 / 43 –
Scheibe
Scheibe
Die Gleichungen geben jeweils den verträglichen Gleichgewichtszustand in X1 – und
X2 –Richtung des Fachwerks und der Scheibe an, vgl. (Bild 6.1). Mit tanα = sinα / cosα
folgt, daß Gl. (6.14.2) und Gl. (6.14.3) identisch sind, die Wirkung von �K 11 in X2 –Richtung
also übereinstimmt mit der Wirkung von �K 22 in X1 –Richtung, was als indirekte
Bestätigung des Symmetriesatzes von Maxwell–Betti gedeutet werden kann. Aus dem
Einwirken der symmetrischen (s) Scheibendehnungen ergeben sich daher drei unabhängige
Bestimmungsgleichungen, um drei Stabflächen in eindeutiger Weise zu ermitteln.
Es ist
A s 1 � A 0 fs 1 ,
A s 2 � A 0 fs 2 ,
A s 3 � A 0 fs 3 .
Die Grundfläche aller Stäbe beträgt nach Gl. (6.16.1) wiederum
A0 � 3
at ,
16
(6.26.1)
(6.26.2)
(6.26.3)
während die Faktoren nun zusätzlich von der Querdehnzahl ν abhängen. Im Einzelnen
ergeben sich als neue Werte nach Gl. (6.26.1 bis 6.26.3) folgende Faktoren:
fs �
8
1 3
1 (tan� � �cot�) ,
�1 � �2� (6.27.1)

fs �
8
2 3
fs �
8
3 3
1
�1 � � 2� �1 � �tan 2 �� ,
1
�1 � � 2�
�
sin�cos 2 � .
– 6 / 44 –
(6.27.2)
(6.27.3)
Aus der Einwirkung der antimetrischen (a) Scheibengleitung � K 12 � �� K 12 � �K 21 � er–
geben sich zwei weitere Gleichungen, nämlich Gl. (6.14.5)
A3sin2�cos� �
at tan�
Fachwerk Scheibe
4(1 � �)
und Gl. (6.14.6)
A3sin�cos2� �
at
Fachwerk Scheibe
4(1 � �) .
Mit tanα = sinα / cosα erkennt man, daß auch sie übereinstimmen. Damit ist eine weitere
unabhängige Stabfläche für die Diagonalen bekannt, die sich mit dem Faktor
zu
fa �
4
3 3
A a 3 � A 0 fa 3
1
(1 � �)
1
sin�cos 2 �
(6.28.1)
(6.28.2)
errechnet. In der vorliegenden Form können die Stabflächen Gl. (6.27) bis Gl. (6.28)
noch nicht in einem Gitterrost verwendet werden. Man erkennt dies daran, daß für den
Sonderfall ν = 1/3 sowohl Gl. (6.27.3) als auch Gl. (6.28.1) auf den Wert von Gl. (6.16.4)
führen. Für ν ≠ 1/3 würde sich also für die Diagonalen eine doppelte Stabfläche ergeben,
wenn die Stabflächen As 3 und Aa 3 gleichwertig in die Analogie zwischen Scheibe
und Fachwerk eingehen. Eine eindeutige Zuordnung ergibt sich dagegen, wenn die
Stabflächen der Diagonalen in einen Grund– und in einen Korrekturwert aufgespalten
werden, die im Sonderfall ν = 1/3 mit einem Wert von Gl. (6.16.4) übereinstimmen müssen.
As 3 folgt aus einer reinen Längsbesanspruchung, ist also einer symmetrischen Stabdehnung
�s 3 zuzuordnen. Aa 3 folgt dagegen aus einer reinen Schubbeanspruchung.
Sie führt zu einer reinen Schiefstellung des Gitterrostes, so daß eine antimetrische
Stabdehnung �a 3 in den Diagonalen auftritt. Für die Stabkraft N3, z.B. der AC–Diagonalen
gilt somit ganz allgemein
N 3,AC � EA 3,AC � 3,AC � E�A s 3 �s 3 � Aa 3 �a 3 � AC .
(6.29)

Der symmetrische Anteil der diagonalen Dehnung ε3,AC ist durch
�s �
1
3,AC 2 ��3,AC � � � 3,BD
bestimmt und der antimetrische Anteil durch
�a �
1
3,AC 2 ��3,AC � � � 3,BD .
Sie sind im (Bild 6.26a und b) dargestellt.
D’
D
N 3
A’ B’
A B
a) Symmetrischer Anteil ε3,AC Bild 6.26 : Stabdehnungen der Diagonalen
Wird nun Gl. (6.30) in Gl. (6.29) eingesetzt, folgt
C
C’
N 3,AC � E� 1
2 �A s 3 � Aa 3 �� 3,AC � 1
2 �A s 3 � Aa 3 �� 3,BD� .
– 6 / 45 –
A’
D
D’
N 3
A B
C
B’
C’
b) Antimetrischer Anteil ε 3,AC
(6.30.1)
(6.30.2)
(6.31)
Gl. (6.31) zeigt, daß sich für ν ≠ 1/3 die Diagonalen in einem rechteckigen Gitterrost
gegenseitig beeinflussen. Der Grundwert der Stabfläche der AC–Diagonalen korrespondiert
mit der Dehnung der AC–Diagonalen ε 3,AC. Er ist durch Gl. (6.31) bekannt und
wird als dritte Stabfläche im Gitterrost eingeführt.
A3 � 1�A
s � Aa
2 3 3� � A0f3 .
(6.32.1)
Der Korrekturwert ist mit der Dehnung der BD–Nebendiagonalen verknüpft. Er ist durch
Gl. (6.31) ebenfalls bekannt und wird als vierte Stabfläche im Gitterrost eingeführt.
A4 � 1�A
s � Aa
2 3 3� � A0f4 .
(6.32.2)
Die Faktoren der Grund– und Korrekturwerte errechnen sich aus Gl. (6.27.3) und
Gl. (6.28.1) zu
und
f3 � 1�f
s � fa
2 3 3� � 2
3
f4 � 1�f
s � fa
2 3 3� � 2
3
1 � �
�1 � � 2�
3� � 1
�1 � � 2�
1
sin�cos 2 �
1
sin�cos 2 � .
(6.33.1)
(6.33.2)

Für den Sonderfall ν = 1/3 folgt aus Gl. (6.33.1)
und
f 3 �
f 4 � 0.
1
sin�cos 2 � � f 3
� Gl. (6.16.4)
Das einfache (ν = 1/3) und das verallgemeinerte Modell (ν beliebig) stimmen also
für den Sonderfall ν = 1/3 überein. Sie sind damit konsistent. Das verallgemeinerte
Modell ist natürlich aufwendiger, da es pro Diagonale zwei unabhängige Stäbe benötigt,
um den Einfluß einer Querdehnzahl ν ≠ 1/3 zu erfassen. Es sollte daher nur dann zur
Anwendung kommen, wenn die aktuelle Querdehnzahl besonders stark vom Sollwert
ν = 1/3 des einfachen Modells abweicht, das den Standardfall der Gitterrostmethode
für viereckig begrenzte Wandscheiben darstellt. Ein direkter Vergleich zwischen dem
einfachen und dem verbesserten Modell ist (Bild 6.27) zu entnehmen.
Einfaches Modell ν = 1/3 :
Standardfall der Anwendung
A 1
α
A0 � 3
at ,
16
A 2
A 2
An � A 0 fn , n � 1, 2, 3
mit
f 1 � (3tan� � cot�) ,
f 2 � �3 � tan 2 �� ,
f 3 �
1
sin�cos 2 � .
A 3
A 1
(6.16.1)
(6.16.2)
(6.16.3)
(6.16.4)
Bild 6.27 : Einfaches und verallgemeinertes Scheiben–Gitterrostmodell
A 1
A 3
– 6 / 46 –
Verallgemeinertes Modell ν = beliebig :
Nur in Ausnahmefällen anwenden
A 2
A 2
A 4
A 1
A0 � 3
at , (6.16.1)
16
An � A 0 fn , n � 1, 2, 3, 4
mit
f1 � 8 1 (tan� � �cot�) ,
3 �1 � �2� (6.34.1)
f2 � 8 1
3 �1 � �2� �1 � �tan2�� , (6.34.2)
f3 � 2 1 � �
3 �1 � �2� 1
sin�cos2 ,
�
(6.34.3)
f4 � 2 3� � 1
3 �1 � �2� 1
sin�cos2 .
�
(6.34.4)
t
a

4.0
3.0
2.0
1.0
0.0
–1.0
–2.0
0.
Bild 6.28 :
f n, n = 1,2,3,4
f 1
f 3
f 2
f 2
f 1
f 4
1/4
Verallgemeinertes
Modell
– 6 / 47 –
1/3
Einfaches
Modell
f 4
f 3
f 1 = f 2
f 2 = f 1
Verallgemeinertes
Modell
Abhängigkeit der Querschnittsflächen von der Querdehnzahl
für ein quadratisches Gitterrost (α = 45°)
1/2
Querdehn–
zahl
Die grafische Auswertung der Flächenfaktoren im (Bild 6.28) zeigt, daß die Abtragung
der Lasten im Gitterrost und damit auch in der Scheibe mit zunehmendem ν stärker
über die Diagonalen erfolgt und mit abnehmendem ν stärker über die Seitenstäbe. Die
Stabfläche der zusätzlichen Diagonalen f 4 nimmt im Bereich zwischen ν = 0 und
ν = 0.333 negative Werte an, vgl. (Bild 6.28). Aus mathematischer Sicht ist damit zwar
die Gleichheit zwischen den statischen Modellen Scheibe und ebenes Fachwerk gewährleistet,
aus ingenieurmäßiger und auch aus numerischer Sicht sind aber negative
Stabflächen nicht als sinnvoll anzusehen. Auch aus dieser Sicht spricht daher alles für
die Anwendung der einfachen Modelle mit dem Festwert ν = 1/3.
ν

6.3 Platte und Rahmenwerk
6.3.1 Einleitung
Analytische Lösungen der Plattengleichung ∆∆u 3 = p 3 / B für technisch interessante
Anwendungen sind nur im beschränkten Umfang bekannt, vgl. Teil 4: Plattentheorie.
Es ist daher sinnvoll, auch im Fall der Platten Überlegungen darüber anzustellen, welche
baustatisch orientierte Vorgehensweisen sich anbieten, um zumindest Näherungen
von Plattenlösungen ermitteln zu können.
Sehr beliebt ist z.B. in der Praxis das sehr einfache Modell von gekreuzten Balken. Die
Verteilung der Flächenlast auf die beteiligten Balken folgt dabei aus dem Vergleich
der größten Duchbiegung in Plattenmitte. Das Verfahren hat u.a. auch Eingang in die
DIN 1045 gefunden. Erhöht man die Anzahl der gekreuzten Balken, entsteht ein Trägerrost,
das aus statischer Sicht einem liegenden Rahmen dargestellt. Als Varianten sind
vereinfachte und verbesserte Trägerroste bekannt, die sich hinsichtlich der Genauigkeit
erheblich voneinander unterscheiden.
Gekreuzte Balken und vereinfachte Trägerroste beruhen auf anschaulichen Gleichgewichtsbetrachtungen
und verletzen in der Regel die Verträglichkeitsbedingungen. Plattentragwerke,
deren Bemessung auf solchen Näherungssätzen beruhen, sind daher
zusätzlich durch konstruktive Maßnahmen zu ertüchtigen, um im Berechnungsansatz
nicht erfaßte Tragwirkungen abzudecken. Dies gilt besonders für die Torsionsbewehrung
in den Plattenecken, die von gekreuzten Balken gar nicht und von vereinfachten
Trägerrosten nur unzureichend erfaßt wird. Für viele Problemstellungen aus der Praxis
ist dies aber trotzdem eine durchaus plausible Vorgehensweise. Sie hat nur dort ihre
Grenzen, wo die Flächenwirkung von Platten eindeutig domoniert. Zur Erfassung der
Plattenwirkung mit baustatischen Methoden bietet sich wie schon bei den Scheiben wiederum
die Gitterrostmethode an. Der Mehraufwand von Gitterrosten– bzw. verbesserten
Trägerrostmodellen ist im Vergleich zu vereinfachten Trägerrostmodellen gering,
der zusätzliche Gewinn an Genauigkeit aber sehr groß.
Am Beispiel einer massiven Brückenplatte im (Bild 6.29) ist dargestellt, wir die Mo–
dellanalogie zwischen Plattenkonstruktion und Rahmenwerk aussehen könnte.
(Bild 6.29a) zeigt das statische System der Brückenplatte als Kontinuum nach der Plattentheorie
und (Bild 6.29b) als Rahmenwerk nach der Gitterrosttheorie. Die Zustandsgrößen
von Stahlbetonplatten in Brückenbauwerken sind nach DIN 1075 mit Hilfe der
Plattentheorie zu bestimmen. Eine Idealisierung der Platte als vereinfachtes Trägerrost
reicht daher nicht aus, um dieser Forderung gerecht zu werden. Die Trägheitsmomente
in den Querschnitten der Trägerroststäbe sind vielmehr auf der Grundlage der Gitterrosttheorie
zu ermitteln, um die Vergleichbarkeit der Lösungen zwischen Platte und liegendem
Rahmenwerk bzw. Trägerrost zu gewährleisten.
– 6 / 48 –

h
Freier Rand
a
t
L 1
Bild 6.29 : Statische Systeme einer Brückenplatte aus Stahlbeton
R
X3
X 2
SLW 60
R = 600 kN
Elastomere Auflager mit
E–Modul EL a) Kontinuum: Modell nach der Plattentheorie
R
4
– 6 / 49 –
Stahlbetonplatte
mit E, ν
b) Rahmenwerk bzw. Trägerrost: Modell nach der Gitterrosttheorie
R
4
R
4
R
4
C 33 � E L ab
h
L 2
Widerlager
Plattenmittelfläche
X 1
In : Trägheitsmomente
des n–ten Stabes
im Träger– bzw.
Gitterrost.

6.3.2 Trägheitsmomente der Gitterroststäbe
Durch die Analogie zwischen Scheibe und Fachwerk ist die Querschnittsfläche der Gitterroststäbe
bekannt. Eine Aussage über den geometrischen Aufbau der Stabquerschnitte
ist damit allerdings nicht verbunden. Sie ist auch nicht erforderlich, da für die
Berechnung nur der reine Zahlenwert interessiert. Ohne Verlust an Information kann
man daher von einem Rechteck als Ersatzquerschnitt ausgehen, wie er ja auch bei
Scheiben und Platten wirklich auftritt. Dann besteht zwischen den Stabflächen A n im
Scheibengitterrost (Bild 6.1) und den Trägheitsmomenten I n im Plattengitterrost
(Bild 6.29) der einfache Zusammenhang
mit
In � An t2
12 � I 0 fn , n � 1, 2, 3, (4) (6.35.1)
t 2
I0 � A0 12
� at3
64
. (6.35.2)
Bei der Anwendung von ebenen Stabwerksprogrammen ist die Zuordnung der Trägheitsmomente
im Träger– bzw. Gitterrost eindeutig und bedarf keiner weiteren Über–
legung. Es ist aber darauf zu achten, daß die Vorgabe der Querschnitts– und Last–
werte mit der Position eines liegenden Rahmenwerks in einer horizontalen Ebene korrespondiert,
vgl. (Bild 6.29). Da dies vielfach nicht möglich ist, sind in der Regel räum–
liche Stabwerksprogramme anzuwenden.
Bei der Anwendung eines räumlichen Stabwerksprogramms ist sehr genau darauf zu
achten, in welcher Beanspruchungsebene der Stabelemente die zu untersuchende
Platte mit ihrer Mittelfläche liegt. Dies ist von Programm zu Programm verschieden. In
der Regel ist davon auszugehen, daß eine Zuordnung zwischen der Plattenmittel–
fläche und der globalen (X 1 – X 2 )–Beanspruchungsebene vorliegt. Diese Situation ist im
(Bild 6.30) dargestellt. Die Angabe der lokalen Querschnittswerte hat in Richtung der
Hauptachsen (u, v, w) zu erfolgen. Die Verschiebung u zeigt in Richtung der Stabachse.
Die Verschiebungen v und w sind um 90° versetzt senkrecht dazu angeordnet. Die
Trägheitsmomente drehen um die Hauptachsen.
Das Trägheitsmoment I u der Torsionssteifigkeit und das Trägheitsmoment der Steifigkeit
von einer Richtung der Doppelbiegung – hier I w – sind vakant, da sie beim Gitter–
rostelement nicht auftreten. Im Rahmen der numerischen Berechnung sind sie daher
durch das Setzen kleiner fiktiver Zahlen zu unterdrücken. Bei einer Anordnung der Plattenmittelfläche
in der (X 1 – X 3 )– oder (X 2 – X 3 )–Ebene ist entsprechend zu verfahren.
Die Ermittlung der Plattenmomente kann in gleicher Weise erfolgen wie die Ermitt–
lung der Scheibenkräfte. Dazu ist in der Verträglichkeitsbedingung Gl. (6.18) lediglich
(n 11 , n 22 , n 12 = n 21 ) durch (m 11 , m 22 , m 12 = m 21 ) und N n durch M n zu ersetzen. Der
formale Austausch der Scheibengrößen durch die entsprechenden Plattengrößen gilt
auch für die vereinfachten Gleichgewichtsmodelle Gl. (6.23 bis 6.24), da sich die Verteilungslängen
der Stabkräfte und Stabmomente nicht verändern.
– 6 / 50 –

2
1
X 3
a) Seitenstäbe 1 und
X 3
b) Diagonalstäbe
I u
I w
3
w
v
w
u v
I v = I 1
v
u
2
w
I w
3
I u
I v = I 3
u
I v = I 2
Bild 6.30 : Zusammenhang zwischen Plattenmittelfläche und globaler
Beanspruchungsebene
I u
I w
u
v
I u
– 6 / 51 –
X 2
I w
I v = I 2
w
v
X 2
I v = I 3
w
I v = I 1
u
I w
I w
u
I u
v
w
I u
(I u, I w) = 0 → (1.E –10 )
3
X 1
Plattenmittelfläche in der
globalen (X1 – X2 )–Bean–
spruchungsebene
(I u, I w) = 0 → (1.E –10 )
1
2
X 1

6.3.3 Beispiel: Konvergenzverhalten von Platten–Gitterrostelementen
6.3.3.1 Quadratische Platte
Eine quadratische Platte – L = L 1 = L 2 – mit einer nach unten gerichteten Flächenbe–
lastung p 3 = konst. soll mit unterschiedlichen Gitterrostunterteilungen untersucht werden,
um die Lösungsqualität der Methode abschätzen zu können. Als Unterteilung sind
quadratische Raster mit 2×2, 4×4, 6×6, 8×8 und 10×10 Gitterrostelementen mit fester
Querdehnzahl ν = 1/3 vorgesehen. Die Berechnungen erfolgen für die Randbedingungen
’Gelenkige Lagerung’ und ’Feste Einspannung’ aller Plattenränder. Das statische
System der Quadratplatte ist im (Bild 6.31) dargestellt.
Die Durchbiegung und die Biegemomente in Plattenmitte sind in normierter Form
in Abhängigkeit vom Raster ausgewertet und als Konvergenzkurven dargestellt. Im
(Bild 6.32) sind die Werte der Lösung bei gelenkig gelagerten Plattenrändern veranschaulicht
und im (Bild 6.33) bei fester Einspannung. Zusätzlich sind in den (Bildern 6.32
und 6.33) weitere Lösungen eingetragen, um die Gitterrostlösung zu kontrollieren und
zwar eine analythische Plattenlösung nach Czerny /20/ für die Querdehnzahl ν = 0, eine
numerische Plattenlösung mit dem FE–Programm HYDAS /13/ für die Querdehnzahl
ν = 1/3 sowie eine Näherungslösung nach Stiglat/Wippel /21/, die auf der Annahme
einer drillweichen Platte beruht, also im wesentlichen dem Modell von zwei gekreuzten
Balken entspricht. In beiden Fällen konvergiert die Gitterrostlösung zur HYDAS–
Lösung, die hier als Vergleichslösung dient, da sie voll mit der schubstarren Plattentheorie
übereinstimmt. Die analytischen Lösungen beruhen ebenfalls auf der schubstarren
Plattentheorie. Die Abweichungen zur Gitterrost– bzw. HYDAS–Lösung sind eine
Folge der unterschiedlichen Querdehnzahlen.
Die Näherungslösung liegt dagegen nicht mehr im Geltungsbereich der Plattentheorie.
Platten tragen Lasten über Biege– und Torsionswirkung ab. Verwindungen der Platte
sind vor allem in Richtung der Diagonalen zu erwarten. Dies gilt besonders für die Eckbereiche
gelenkig gelagerter Platten (Bild 6.34). Kann die Platte hier frei abheben, können
sich keine Torsionsmomente einstellen, da kein Zwang vorliegt (Bild 6.34a). Verhindern
dagegen geeignete konstruktive Maßnahmen ein Abheben der Ecken, treten als
Reaktionen Torsionsmomente und Auflagerkräfte auf, wobei die Torsionsmomente in
Richtung der Diagonalen als Biegung wirken (Bild 6.34b).
Wird die Torsionssteifigkeit vernachlässigt, kann sich kein Biegezustand entlang der
Diagonalen einstellen. Der Lastabtrag erfolgt ausschließlich über Biegemomente, so
daß diese Werte zwangsläufig erheblich größer ausfallen, da sie den Traganteil der vernachlässigten
Torsionswirkung indirekt mit übernehmen müssen. Besonders deutlich
ist dieses Verhalten im Fall der eingespannten Platte (Bild 6.33) zu erkennen. Durch die
Volleinspannung kann sich im Eckbereich von vornherein keine Verwindung und damit
auch kein Torsionsmoment einstellen. Der Lastabtrag über die Biegemomente dominiert
und folgerichtig weichen nun auch die Momente der torsionsweichen und torsionssteifen
Lösung kaum voneinander ab. Bei den Durchbiegungen bleibt die Differenz zwischen
den unterschiedlichen Lösungsansätzen dagegen bestehen, da sich hier nach
– 6 / 52 –

wie vor der Verlust der Torsionssteifigkeit auswirken muß, der im Vergleich zu torsionssteifen
Platten zu erheblich größeren Durchbiegungen führt, vgl. (Bilder 6.32 und
6.33).
L 2 = L
Randbedingung:
Gelenkige Lagerung.
X 2
L 1 = L
a) Platten–Gitterrostelement (hier: 4×4 Raster
1
3
I 1
2
ϕ 2, m 2
b) Trägheitsmomente der Stäbe
in einem Gitterrost
I 3
– 6 / 53 –
Randbedingung:
Feste Einspannung.
u3 = 0 ,
m1 = 0 . u3 = 0 ,
ϕ2 = 0 .
I 2
u3 = 0 ,
m2 = 0 .
Bild 6.31 : Statisches System einer Quadratplatte
I 2
I 3
1
I 1
2
3
u3 = 0 ,
ϕ2 = 0 .
a
Knoten
E, t
ν = 1/3
α
X 1
atanα
ϕ 1, m 2
�p3a2tan�� 4
b) Resultierende Lasten in den Knoten
eines Gitterrostes
(in negativer X 3 –Richtung wirkend)

98.4
55.0
50.0
45.0
40.0
35.0
30.0
Bild 6.32 :
� u3 �
L
0.076
0.055
0.050
0.045
0.040
0.035
0.030
�m 11�
�p 3 ⋅L
�m 11�
�p 3 ⋅L
2� = �m 22�
�p 3 ⋅L 2�
2� = �m 22�
�p 3 ⋅L 2�
2
4
� u3 �
L
Max. Momente und max. Durchbiegung in Plattenmitte einer allseitig
frei drehbar gelagerten Quadratplatte
– 6 / 54 –
N
A
H
X 3 ,u3
6
p 3
8
: Gitterrost
X 2
m 22
m 11
X 1
10
N
N
H
A
H
A
Anzahl der Elemente
: Näherungslösung /21/
: Analytische Lösung /20/
: FE–Programm HYDAS /13/

21.6
14.0
13.5
13.0
Bild 6.33 :
� u3 �
L
18.0 0.060
17.5 0.055
17.0 0.050
16.5 0.045
16.0 0.040
15.5 0.035
15.0 0.030
14.5 0.025
0.020
0.015
0.010
�m 11�
�p 3 ⋅L
�m 11�
�p 3 ⋅L
2� = �m 22�
�p 3 ⋅L 2�
2� = �m 22�
�p 3 ⋅L 2�
2
4
� u3 �
L
Max. Momente und max. Durchbiegung in Plattenmitte einer allseitig
fest eingespannten Quadratplatte
– 6 / 55 –
N
A
H
X 3 ,u3
6
p 3
8
: Gitterrost
X 2
m 22
m 11
X 1
10
N
A
N
H
A
H
Anzahl der Elemente
: Näherungslösung /21/
: Analytische Lösung /20/
: FE–Programm HYDAS /13/

X 3 ,u 3
a) Platte mit frei abhebenden Ecken
X 3 ,u 3
p 3 = konst.
p 3 = konst.
A = 2m 12
X 2
X 2
X 1
A A
b) Platte mit gehaltenen Ecken
A
X 1
m 21
– 6 / 56 –
m 12
–m 21
m 21 = m 12 = 0
–m 12
–m 21
m 12 = 0
–m 12 m 12
Bild 6.34 : Durchbiegung und Torsionsmomente gelenkig gelagerter Platten
m 21

6.3.3.2 Rechteckige Platte
Quadratische Platten sind hinsichtlich ihres Tragverhaltens als optimal einzuschätzen.
Dies drückt sich auch in der Steifigkeitsbelegung der Gitterroststäbe aus. Das Verhältnis
der Trägheitsmomente zwischen Seiten– und Diagonalstäben ist für α = 45° ebenfalls
als optimal anzusehen. Um abschätzen zu können, wie sich Gitterroste mit α ≠ 45° verhalten,
soll zusätzlich eine rechteckige Platte untersucht werden. Dazu wird unter sonst
gleichen Voraussetzungen lediglich die L 2–Länge der quadratischen Platte (Bild 6.31)
verdoppelt.
Das statische System der Rechteckplatte ist im (Bild 6.35) dargestellt. Als Unterteilung
sind sowohl rechteckige (Bild 6.35a) als auch quadratische Raster (Bild 6.35b) vorgesehen.
Die untersuchten Varianten enthalten beim Rechteckraster 2×2, 4×4, 6×6 und 8×8
Gitterroste. Das Quadratraster weist mit 2×4, 4×8. 6×12 und 8×16 Gitterrosten in
X 2 –Richtung eine doppelt so feine Teilung auf wie das Rechteckraster. Beim Rechteckraster
wird mit α = 26.57° der untere Grenzwinkel von α = 30° unterschritten, so daß
die I 1–Trägheitsmomente (Bild 6.30a) negative Werte annehmen. Beim Quadratraster
mit α = 45° ist dagegen ein Optimum der I–Verteilung erreicht.
Die Ergebnisse der Untersuchungen sind für die maximalen Werte in Plattenmitte ausgewertet
und in den (Bildern 6.36 und 6.37) dargestellt. Die Vergleichsergebnisse mit
HYDAS /13/ sowie nach der analytischen /20/ und genäherten Lösung /21/ sind ebenfalls
eingetragen. Beide Gitterrost–Lösungen konvergieren für die untersuchten Randbedingungen
’Gelenkige Lagerung’ (Bild 6.36) und ’Feste Einspannung’ (Bild 6.37) zu
den HYDAS–Lösungen, die auf der schubstarren Plattentheorie beruhen. Im Konvergenzverhalten
zeigen sie aber deutliche Unterschiede. Die Lösungen mit quadratischen
Gitterrosten (Bilder 6.36b und 6.37b), die eine reguläre Steifigkeitsbelegung aufweisen,
konvergieren monoton. Bei den Rastern mit rechteckigen Gitterrosten (Bilder
6.36a und 6.37a) treten dagegen Störungen auf. Die Konvergenz erfolgt nicht mehr
monoton. Sie weist zwischen den Rastern einen unstetigen Verlauf auf, der erst mit zunehmender
Rasterteilung abnimmt. Dies ist eindeutig auf die irreguläre Steifigkeitsbelegung
der rechteckigen Gitterroste zurückzuführen. Die negativen I 1–Werte ergeben im
Gesamtsystem negative Steifigkeiten auf der Hauptdiagonalen der Gleichungsmatrix,
die aus der Anwendung des Verfahrens der Stabsteifigkeiten resultiert. Die Numerik
muß dann mit nicht positiv definierten Gleichungsmatrizen durchgeführt werden. Eine
monotone Konvergenz ist daher nicht zu erwarten. Vielmehr kann sich sogar eine falsche
Konvergenz einstellen, die Lösung also zu falschen Grenzwerten konvergieren.
Um solches Verhalten von vornherein auszuschließen, ist bei der Anwendung der Gitterrostmethode
immer darauf zu achten, daß die Winkelbegrenzung
30° ≤ α ≤ 60°
in jedem Gitterrost eingehalten wird.
– 6 / 57 –

L 2
α
X 2
L 1
a) Rasterteilung mit rechteckigen Gitterrosten (hier: 4×4 Teilung
und α = 26.57° < 30°
L 2
α
L 1
b) Rasterteilung mit quadratischen Gitterrosten (hier: 4×8 Teilung
und 30° ≤ α = 45° ≤ 60°
Bild 6.35 : Statisches System einer Rechteckplatte mit L 2 = 2L 1
– 6 / 58 –
X 1

25.0
20.0
15.0
10.0
a)
5.0
� u3 �
L
0.150
0.125
0.100
0.075
0.050
�m 11�
�p 3 ⋅L 2�
�m 11�
�p 3 ,
⋅L2� �m 22�
�p 3 ⋅L 2�
2 4 6 8
�m 22�
�p 3 ⋅L 2�
Max. Momente und max.
Durchbiegung bei einem
Seitenverhältnis der
Gitterrostelemente von
α = 26.57°.
Bild 6.36 : Allseitig frei drehbar gelagerte Rechteckplatte
� u3 �
L
– 6 / 59 –
b)
X 3 ,u3
N
A
H
X 2
p 3
: Gitterrost
m 22
2 4 6 8
m 11
X 1
: Näherungslösung /21/
: Analytische Lösung /20/
N
N
H
A
A
H
H
N
A
Anzahl der
Elemente
: FE–Programm HYDAS /13/
Max. Momente und max.
Durchbiegung bei einem
Seitenverhältnis der
Gitterrostelemente von
α = 45°.

4.50
4.25
3.75
3.50
3.25
3.00
Bild 6.37 :
� u3 �
L
0.060
4.00 0.050
a)
0.040
0.030
0.020
0.010
�m 11�
�p 3 ⋅L 2�
�m 11�
�p 3 ,
⋅L2� �m 22�
�p 3 ⋅L 2�
2 4 6 8
�m 22�
�p 3 ⋅L 2�
Max. Momente und max.
Durchbiegung bei einem
Seitenverhältnis der
Gitterrostelemente von
α = 26.57°.
� u3 �
L
– 6 / 60 –
X 3 ,u3
Allseitig fest eingespannte Rechteckplatte
b)
N
A
H
X 2
p 3
: Gitterrost
m 22
2 4 6 8
m 11
X 1
: Näherungslösung /21/
: Analytische Lösung /20/
N
N
H
A
A
H
H
N
A
Anzahl der
Elemente
: FE–Programm HYDAS /13/
Max. Momente und max.
Durchbiegung bei einem
Seitenverhältnis der
Gitterrostelemente von
α = 45°.

6.4 Hinweise zur Benutzung von Programmen
6.4.1 Allgemeines
Es sind die Querschnittsflächen und Trägheitsmomente der Gitterroststäbe zu ermitteln,
um Scheiben– und Plattenprobleme einzeln oder in kombinierter Form mit Programmen
für Stabtragwerke zu berechnen. Wie dies im einzelnen zu geschehen hat,
ist im (Bild 6.38) zusammengestellt. Mit der dort angegebenen Vorgehensweise können
z.B. Wandscheiben und Deckenplatten zwangslos in die Rahmenberechnung von Skelettbauten
integriert werden. Dies ist besonders interessant, wenn es darum geht, globale
Aussteifungskonzepte zu entwickeln.
Bei der Bestimmung der Scheibenkräfte und Plattenmomente aus den Schnittgrößen
der Gitterroststäbe kann in der Regel in einfacher Weise verfahren werden. Im
(Bild 6.39) erfolgt die Verteilung der Stabkräfte und Stabmomente im Sinne eines
Gleichgewichtsmodells. Die Verteilungslängen der Längskräfte und Biegemomente
werden jeweils durch die Kreuzungspunkte benachbarter Diagonalen begrenzt und
die Verteilungslängen der Schubkräfte und Torsionsmomente durch Projektionen
senkrecht zu den Diagonalen mit der zusätzlichen Bedingung, daß sich die Projektionen
auf dem Wirkungsrand der Flächengrößen schneiden.
6.4.2 Genauigkeit
Die Analogie zwischen den Modellen Scheibe oder Platte und Gitterrost beruht auf der
Annahme, daß sich ein endlich begrenzter Ausschnitt aus dem Flächentragwerk durch
ein Gitterrost aus Stäben statisch und geometrisch gleichwertig ersetzen läßt. Dazu
werden beiden Systemen Einheits–Verzerrungszustände eingeprägt und die Flächen–
und Trägheitsmomente im Gitterrost aus der Forderung bestimmt, daß Gleichgewicht
und Verträglichkeit in beiden Systemen übereinstimmen müssen.
Das Einprägen der Verzerrungszustände erfolgt im Rahmen eines Koeffizientenvergleichs.
Der Vergleich ist damit auf konstante Verzerrungen beschränkt. Die Übereinstimmung
zwischen einem beliebigen Flächenausschnitt und einem zugeordneten Gitterrost
gilt daher nur für konstante Spannungsverteilungen. In realen Konstruktionen
des Bauwesens treten i.a. aber mehr oder weniger nicht konstant verteilte Spannungszustände
auf. Es sind daher eine Vielzahl von Gitterrostelementen erforderlich, um sie
zu erfassen. Nur wenn es darum geht, den stabilisierenden Einfluß von Wand– und
Deckenscheiben nachzuweisen, reicht eine grobe Gitterrosteinteilung aus. Wieviel
Gitterrostelemente jeweils zu verwenden sind, hängt stark vom aktuellen Problem ab
und ist vorab sorgfältig zu untersuchen, ggf. auch durch vergleichende Untersuchungen
an stark vereinfachten Systemen.
– 6 / 61 –

a
a) Scheibenanteil für ν = 1/3
a
1
α
b) Plattenanteil für ν = 1/3
1
α
3
3
3
3
2
2
2
2
1
1
– 6 / 62 –
Flächen der Gitterroststäbe:
A 1 � A 0 �3tan� � cot�� � 0,
A 2 � A 0 �3 � tan 2 �� � 0,
A3 � A
1
0
sin� � cos2 � 0,
�
A0 � 3
at ,
16
t = Dicke der Scheibe.
Trägheitsmomente der
Gitterroststäbe:
I 1 � I 0 �3tan� � cot�� � 0,
I 2 � I 0 �3 � tan 2 �� � 0,
I3 � I
1
0
sin� � cos2 � 0,
�
I 0 � 1
64 at3 ,
t = Dicke der Platte.
Die Zuordnung zwischen den Flächen A der Gitterroststäbe und den lokalen Querschnittswerten
der Stabelemente ist eindeutig und bedarf keines weiteren Hinweises.
Bei der Zuordnung der Trägheitsmomente I ist dagegen die räumliche Lage der Gitterrostelemente
zu beachten, von der es abhängt, ob die Biegung und Torsion der Platte
mit I v um die lokale Querschnittsachse v oder mit I w um die lokale Querschnitts–
achse w der Stabelemente erfolgt, vgl. (Bild 6.30). Der nicht besetzte Biegewert ist in
der Datenvorgabe durch eine kleine Zahl anzunähern. Ebenso der Querschnitts–
wert I u der Stabtorsion, der bei Gitterrostelementen ersatzlos entfällt.
c) Zuordnung
Bild 6.38 : Gitterrostelemente: Querschnittswerte

a) Schnittgrößen n 11 und m 11
m 22
M
L 22
Gitterroststab:
n 22
N (kN), M (kNm) .
Scheibe:
n 22 � N
L 22
Platte:
m 22 � M
L 22
N
N
� kN m � .
� kNm
m � .
M
b) Schnittgrößen n 22 und m 22
L 11
Scheibe:
n 12 � N
L 12
Platte:
m 12 � M
L 12
– 6 / 63 –
m 11
Bild 6.39 : Gitterrostelemente: Scheiben– und Plattenschnittgrößen
M
N
N
Gitterroststab:
N (kN), M (kNm) .
Scheibe:
n 12 �
Platte:
m 12 �
� N
L 12
� M
L 12
M
� kN m � .
n 11
� kNm
m � .
� kN m � .
� kNm
m � .
c) Schnittgrößen n 12 und m 12
M
N
N
M
Gitterroststab:
N (kN), M (kNm) .
Scheibe:
n 11 � N
L 11
Platte:
m 11 � M
L 11
L 12
L 12
� kN m �
� kNm
m �
n 12
m 12
n 12
m 12

6.4.3 Berechnung einer Aussteifungsscheibe
Im (Bild 6.40) ist die Aussteifungsscheibe eines 20. m hohen Gebäudes dargestellt.
Sie soll die resultierenden horizontalen Stockwerkseinwirkungen F1 bis F5 , die in
unterschiedlichen Höhen angreifen, auf 12. m Gründungsbreite in den Baugrund ein–
leiten. Die Scheibe ist durch sechs, 2×3 = 6 m2 große Öffnungen geschwächt, die in
unterschiedlichen horizontalen und vertikalen Achsen liegen, vgl. (Bild 6.40). Der
Verschwächungsgrad errechnet sich bei 12×20 = 240 m2 Gesamtfläche zu
36
100 � 15%.
240
Im Rahmen einer statischen Berechnung ist die Steifigkeit der geschwächten Scheibe
abzuschätzen. Dies soll mit statischen Modellen von unterschiedlicher Genauigkeit erfolgen.
Für das genaueste Modell ist die Verteilung der resultierenden Verschiebung
und der Verlauf der Trajektorien der Hauptscheibenkräfte darzustellen.
F1
F2
F3
F4
F5
3.
4.5
1.5
3.
1.5
3.
4.5
1.5
4.5
3.5
3.
1.5
3.
2.
X 2 , u 2
1.5 2. 1.5 1. 1. 1.5 2. 1.5
6. 6.
II II
I I
a) System
X
b) Systemwerte
1 , u1 t = 0.30 m , E = 3.4⋅107 kN/m2 , ν = 0.2 .
c) Lasten F1 = 1000. kN , F2 = F3 = F4 = 2000. kN , F5 = 1500. kN .
Bild 6.40 : Durch Öffnungen geschwächte Aussteifungsscheibe
– 6 / 64 –
Symmetrielinie
u1 = ?
0.12 5
6.37 5
7.87 5
20.

Wenn man den 15%–igen Verschwächungsgrad der Scheibe vernachlässigt, bietet sich
als einfachstes statisches Modell ein Kragarm an, um eine Aussage über die Steifigkeit
der Scheibe zu erhalten. Das Kragarmmodell ist im (Bild 6.41) dargestellt. Das Trägheitsmoment
beträgt mit 0.3 m Dicke und 12. m Aufstandsfläche 0.30⋅123
12
� 43.2 m4 .
Die Verschiebung u1 des Kragarmmodells (Bild 6.41) muß mit der horizontalen Verschiebung
u1 in der oberen rechten Scheibenecke (Bild 6.40) übereinstimmen. Die Berechnung
als biegesteifer, aber schubstarrer Kragarm ergibt u1 = 0.72 cm. Erfaßt man
zusätzlich die Schubsteifigkeit des Kragarms GAQ mit G = E/(2(1+ν)) und AQ = (5/6)A,
so erhält man den Wert u1 = 0.96 cm, der im Vergleich zur schubstarren Lösung um
33.3% anwächst.
Will man den Verschwächungszustand der Aussteifungsscheibe (Bild 6.40) dagegen
genauer erfassen, so bietet sich als nächste Stufe eine flächige Modellierung mit der
GRM an, die von einer geometrisch genauen Abbildung der Öffnungen ausgeht. Die
Elementierung ist im (Bild 6.42) dargestellt. Sie bezieht sich wegen der Symmetrie nur
auf das halbe System. Die Einwirkung ist dagegen unsymmetrisch verteilt. Es sind da–
20.
3.
4.5
4.5
4.5
3.5
F 5 = 1000. kN
F 4 = 2000. kN
F 3 = 2000. kN
F 2 = 2000. kN
F 1 = 1500. kN
EI = 14.7⋅10 8 kNm 2
GA Q = 0.43⋅10 8 kN
Bild 6.41 : Kragarmmodell der Aussteifungsscheibe
– 6 / 65 –
X 2 , u 2
X 1 , u 1
a) System b) Verschiebung
Ohne Schubsteifigkeit
u1 = 0.72 cm
u1 = 0.96 cm
Mit Schubsteifigkeit

her zwei Berechnungen am halben System erforderlich, um die Gesamtverschiebung
zu erhalten. Die Lastaufteilung und die zugehörigen Randbedingungen sind ebenfalls
(Bild 6.42) zu entnehmen. Im (Bild 6.42a) sind die Vorgabe des symmetrischen und im
(Bild 6.42b) die Vorgaben des antimetrischen Lastfalls dargestellt. Die Überlagerung
der Ergebnisse us 1 aus der symmetrischen und ua 1 aus der antimetrischen Berechnung
ergibt in der oberen rechten Scheibenecke die horizontale Verschiebung
u1 � us 1 � ua 1 � 1.18 � 0.03 � 1.15 cm.
a) Symmetrischer Lastfall b) Antimetrischer Lastfall
Bild 6.42 : Gitterrostmodell der Aussteifungsscheibe
– 6 / 66 –

Dieser Wert stimmt relativ gut mit dem Wert aus der einfachen Kragarmberechnung
überein, die den Einfluß der Öffnungen vernachlässigt. Die Zunahme der Verschiebung
und damit die Abnahme der Steifigkeit beträgt lediglich 19.8%. Die Hauptabtrags–
richtung muß daher zwischen den Öffnungen verlaufen.
Um diese Vermutung zu überprüfen, wird eine dritte Berechnung mit Hilfe der FEM
durchgeführt. Sie muß von einer sehr feinen Elementierung des halben, oder wie hier,
des ganzen Systems ausgehen. Die feine Elementierung ist erforderlich, um die Singularität
in den Ecken der Öffnungen zu erfassen. Sie entsteht vor allem in scharf einspringenden
Ecken, da hier ein sprunghafter Wechsel der Scheibenkräfte auftritt. Für die
Längskräfte n 11 und n 22 ist dieser Sachverhalt in (Bild 6.43) dargestellt. (Bild 6.43a)
zeigt den Verlauf in scharf einspringenden und (Bild 6.43b) in ausgerundeten Ecken.
∞
n 22 � 0
n r = n 22 = 0
n r = n 11 = 0
∞
a a
n 11 � 0
n 22
X 2 , u 2
n11 n12 n21 Bild 6.43 : Verlauf der Scheibenlängskräfte in Ecken und Öffnungen
– 6 / 67 –
n r = 0
n 11
n 22
n 22
a) Scharf einspringende Ecken b) Ausgerundete Ecken
X 1 , u 1
n 11
b
b

Im Schnitt der Ecke X 1 = –a und X 2 = b ist n 22 links vom Schnitt ungleich Null,
rechts davon wegen des freien Randes der Öffnung aber gleich Null, weil hier die statische
Randbedingung n r = n 22 = 0 gilt. Im Schnitt der Ecke X 1 = –a und X 2 = –b stellt
sich eine vergleichbare Situation für n 11 ein. Unterhalb des Schnitts ist n 11 ungleich
Null, oberhalb des Schnitts wegen des freien Randes der Öffnung aber gleich Null, weil
hier die statische Randbedingung n r = n 11 = 0 gilt. Aus physikalischen Gründen müssen
die Kräfte links und rechts bzw. unten und oben vom Schnitt aber von gleicher Größe
sein. Es müssen daher Zwängungskräfte auftreten, um diesen Zustand zu erreichen.
Dies führt zu einer erheblichen Spannungskonzentration in der unmittelbaren Nähe der
Ecken und in den Ecken selbst zu unendlichen Werten, vgl. (Bild 6.43a).
Werden die Ecken dagegen ausgerundet, ist ein kontinuierlicher Übergang der Scheibenkräfte
n 11 und n 22 möglich, so daß sich wieder endliche Werte einstellen. Diese
Situation ist in den Ecken X 1 = a und X 2 = ±b dargestellt, vgl. (Bild 6.43b). Es bleibt
anzumerken, daß die Ecksingularität nur bei Annahme eines uneingeschränkt elastischen
Materialverhaltens auftritt. In Wirklichkeit wird jedes Material im Bereich von
Spannungskonzentrationen inelastisch reagieren, indem es plastisch wird oder reißt
und dadurch die Spannungskonzentration nicht auftritt.
Störzonen mit geometriebedingten Spannungskonzentrationen sind in der Regel sehr
klein. Sie können daher die Ergebnisse in den ungestörten Bereichen kaum beeinflussen.
Die GRM und die FEM sind Näherungsmethoden. Die GRM beruht auf einer
Analogiebetrachtung zwischen Flächen– und Stabtragwerken. Sie ersetzt Scheiben
durch Fachwerke und Platten durch Trägerroste. Singularitäten in Lösungen von
Flächentragwerken kann sie daher kaum abbilden, so daß sie diese Störungen auch
nicht übertragen kann. Die FEM kann dagegen sehr empfindlich auf Singularitäten reagieren,
weil sie eine stetige Approximation der Lösungsfunktionen voraussetzt. Eine zu
grobe Elementierung der Störzonen führt vielfach zu Oszillationen. Oszillationen können
Singularitäten in ungestörte Bereiche übertragen und damit die Gesamtlösung
stark verfälschen. Dies gilt für Scheiben und Platten.
Die FE–Berechnung der durch Öffnungen geschwächten Scheibe wird mit dem FE–
Programm GEMAS durchgeführt, weil sich gemischt–hybride Elemente als besonders
robust gegenüber Singularitäten erweisen /13/. Sie liefert in der oberen rechten Scheibenecke
als horizontale Verschiebung den Wert u 1 = 1.26 cm , der die Größenordnung
aus der Berechnung mit Gitterrosten bestätigt, da er nur um 9.6% von dieser abweicht.
Der Verlauf der Verschiebungen ist im (Bild 6.44), der Verlauf der Trajektorien der
Hauptkräfte im (Bild 6.45) dargestellt. Der Verlauf der Druck– und Zugtrajektorien bestätigt
die Vermutung, daß die Öffnungen den Lastabtrag nur geringfügig stören. Zwischen
dem einwirkungsbehafteten und dem einwirkungsfreien Rand bilden sich entlang der
Öffnungen zwei Druckdiagonalen aus, die im Druckbereich der Einspannung enden.
Das zugehörige Zugband verläuft parallel zum einwirkungsbehafteten Rand und endet
unmittelbar im Zugbereich der Einspannung. Der innere Bereich der Einspannung ist
weitgehend kräftefrei. Da die Öffnungen den Kräfteverlauf kaum behindern, ist ihr Ein-
– 6 / 68 –

fluß auf die Steifigkeit der Scheibe gering, so daß sich in allen Modellen, die auf unterschiedliche
Näherungsstufen beruhen, Verschiebungswerte in gleicher Größenordnung
einstellen. Es bleibt aber anzumerken, daß dies nicht immer so sein muß, sondern
ausschließlich vom aktuellen Fall abhängt und sich daher von Fall zu Fall ändern kann.
Bild 6.44 : FE–Modell Aussteifungsscheibe. Gesamtverschiebung
– 6 / 69 –

Bild 6.45 : FE–Modell Aussteifungsscheibe. Trajektorien der Scheibenkräfte
In der Aussteifungsscheibe (Bild 6.40) sind die horizontalen Schnitte I und II gekennzeichnet.
Der Schnitt I liegt 0.12 5 m unterhalb des unteren Randes der ersten Dop–
pelöffnung. Er verläuft damit zwar nicht direkt durch die Ecken der Öffnungen, befindet
– 6 / 70 –

sich aber im unmittelbaren Einflußbereich der Singularitäten. Der Schnitt II liegt dagegen
0.12 5 m unterhalb der Mitte der ersten Doppelöffnung und damit außerhalb des
Störbereichs. Die elementweise Verteilung der Scheibenkräfte in beiden Schnitten ist
im (Bild 6.46) dargestellt. Die Auftragung beginnt in der Mitte des linken und endet in
der Mitte des rechten Randelements.
(Bild 6.46a) zeigt die Verteilung im Schnitt I. Im Eckbereich der Öffnungen ist der Einfluß
der Singularität deutlich erkennbar. Die statischen Randbedingungen: n 11 = 0 am linken
und rechten Scheibenrand und n 22 = 0 am unteren Rand der Öffnungen sind sehr gut
angenähert. Eine Abschätzung der Größenordnung ist wegen der Öffnungen und der
sich daraus ergebenden Singularität kaum möglich.
(Bild 6.46b) zeigt die Verteilung im Schnitt II. Am linken Scheibenrand ist die Lasteinleitung
von F 4 erkennbar. Die Größenordnung kann man in einfacher Weise abschätzen.
Die Zusammenhänge sind in der Skizze
F 4 = 2000 kN
Linker Scheibenrand
+
+
0.12 5 0.12 5
0.25
n 11
n 11
– 6 / 71 –
0.12 5
0.12 5
0.12 5
0.12 5
0.25
0.25
dargestellt. Die Last F 4 verteilt sich unter 45° je zur Hälfte auf die beiden anliegen–
den Elemente. Als Einflußbreite von F 4/2 ist die Elementlänge anzunehmen.
Sie beträgt 0.25 m. Damit errechnet sich die horizontale Längskraft zu
n 11 = –1000 kN/0.25 m = –4000. kN/m, ein Wert, der mit dem Ergebnis der FE–Berechnung
im (Bild 6.46b) übereinstimmt. Er fällt bis zum Öffnungsrand auf Null ab und erfüllt
damit die statische Randbedingung. Zwischen den Öffnungen und zwischen der rechten
Öffnung und dem rechten Scheibenrand verschwindet die horizontale Längskraft,
so daß sich hier ein Zustand reiner Balkenbiegung einstellt.

4.50+03
3.00+03
1.50+03
0.
–1.50+03
–3.00+03
–4.50+03
4.50+03
3.00+03
1.50+03
0.
–1.50+03
–3.00+03
–4.50+03
(kN/m)
0. 2.00+00 4.00+00 6.00+00 8.00+00 1.00+01 1.20+01
a) Schnitt I : Unterhalb von zwei Öffnungen
(kN/m)
n 11
n 22
n 12
0. 2.00+00 4.00+00 6.00+00 8.00+00 1.00+01 1.20+01
b) Schnitt II : Durch zwei Öffnungen
Bild 6.46 : FE–Modell Aussteifungsscheibe. Scheibenkräfte
– 6 / 72 –

Die Gesamtverschiebung aus einer FE–Berechnung mit grober Elementierung, die mit
der Netzteilung der GRM im (Bild 6.42) übereinstimmt, ist im (Bild 6.47) dargestellt. Der
Wert der horizontalen Verschiebung in der oberen rechten Scheibenecke errechnet sich
zu u 1 = 1.17 cm. Die Kontrollberechnung bestätigt den Wert u 1 = 1.15 cm aus der Gitterrostberechnung,
die sich damit als durchaus konkurenzfähig zur FEM erweist.
Bild 6.47 : Grobes FE–Modell der Aussteifungsscheibe
– 6 / 73 –

Teil 7: Finite Elemente–Methode (FEM)
7.1 Einführung
Ziel von Teil 7 ist es, eine kurze Einführung in die Berechnung von Flächentragwerken
mit finiten Elementen zu geben, um die grundsätzliche Vorgehensweise der Methode
zu verdeutlichen. Eine ausführliche Darstellung der Methode ist Gegenstand des vertieften
Fachstudiums. Eine Betrachtung aus baustatischer und baudynamischer Sicht
erfolgt z.B. in der Lehrveranstaltung Vertiefung I: Finite Elemente–Methode in der Baustatik
und Baudynamik des Fachgebiets Statik der Baukonstruktionen, die sich vorrangig
mit dem Elementverhalten auseinandersetzt /13/.
Die FEM hat sich im Vergleich zu anderen Verfahren z.B. der Gitterrostmethode wegen
ihrer einheitlichen Vorgehensweise durchgesetzt. Sie erfaßt linien–, flächen– und vo–
lumenförmige Bauteile in grundsätzlich gleicher Weise. Benutzerfreundliche FE– und
Oberflächenprogramme sowie leistungsfähige Arbeitsplatzrechner stehen in großer
Vielfalt zur Verfügung. Man kann daher ohne technische Probleme auch umfangreiche
Aufgabenstellungen mit der FEM im Zusammenhang bearbeiten /22/.
Neben den genannten technischen Voraussetzungen ist aber vor allem ingenieur–
wissenschaftliches Grundwissen erforderlich, um die FEM erfolgreich einsetzen zu
können: Konstruktives Grundwissen ist erforderlich, um Tragwerke mit finiten Elementen
modellieren zu können; Grundwissen der Bauinformatik ist erforderlich, um FE–Programme
und Oberflächen hinreichend sicher benutzen zu können und baustatisches
und baudynamisches Grundwissen ist erforderlich, um die erzielten Ergebnisse ingenieurmäßig
beurteilen zu können. Dieses Grundwissen ist aber in der Praxis bei weitem
nicht in gleicher Weise verbreitet wie der Einsatz von Programmen. Tragwerksberechnungen
mit der FEM, die ohne tiefere Kenntnisse der mathematisch–strukturmecha–
nischen Hintergründe der Methode durchgeführt werden, sind mit einem erheblichen
Sicherheitsrisiko behaftet, da die Übertragung der erzielten Ergebnisse in die Konstruktionsrealität
dann zwangsläufig ohne kritische Bewertung erfolgt /23/.
Die bereits deutlich erkennbare und noch zu nehmende Lücke zwischen Anwendung
der FEM und erforderlichem Theorieverständnis läßt sich nur schließen, wenn potentielle
Benutzer von FE–Programmen neben der reinen Anwendungstechnik auch die
theoretischen Grundlagen der FEM beherrschen. Konstruktives Wissen hängt neben
Grundlagenwissen vor allem von der individuellen Erfahrung ab, die man vorrangig in
der Praxis erwirbt. Die Einarbeitung in die Anwendungstechnik von speziellen FE– und
Oberflächenprogrammen erfolgt in der Regel mit Hilfe von Benutzer–Handbüchern.
Dies ist ein empirischer Vorgang, den man auf der Grundlage von elementaren Kenntnissen
der Bauinformatik am einfachsten ebenfalls in der Praxis nachvollzieht. Die baustatischen
und baudynamischen Kenntnisse sind dagegen Bestandteil des theoretischen
Grundlagenwissens von Bauingenieuren, das man nur in der Universität, nicht
aber in der Praxis erlernen kann.
– 7 / 1 –

Im Rahmen der FEM manifestieren sich die baustatischen und baudynamischen
Kenntnisse in der Beschreibung der Grundlagen und Eigenschaften von finiten Elementen.
Nur mit diesen Kenntnissen kann man statische und dynamische Systeme in physikalisch
zutreffender Weise elementieren, so daß sie das Tragverhalten von Bauwerken
optimal erfassen. Bei Flächentragwerken sind dies in erster Linie Scheiben– und Plat–
tenelemente, die in räumlicher Anordnung als Faltwerkelemente und auf gekrümmten
Flächen als Schalenelemente bezeichnet werden. Die Einführung beschränkt sich auf
den statischen Fall. Es werden einfache Elementvarianten zur Berechnung von Scheiben
und Platten vorgestellt, die auf einer Weggrößenformulierung mit dem PvW beruhen.
Eine detailierte Betrachtung der FEM auf Systemebene ist nicht erforderlich, da
es zwischen Stab– und Flächenelemente keine Unterschiede gibt. Es wird in diesem
Zusammenhang auf die Vorgehensweise beim VdS verwiesen /12/, die in gleicher
Weise für Scheiben– und Plattenelemente gilt.
7.2 Geometrische Definition von finiten Elementen auf Flächen
Beim Ritz–Verfahren im Teil 4, Abschnitt 4.6.2 wurde bereits erwähnt, daß man anstelle
von globalen Ansätzen, die z.B. über das gesamte Gebiet einer Platte verlaufen,
auch lokale Ansätze verwenden kann, die sich nur über Teilflächen des Plattengebiets
erstrecken. Allerdings müssen die lokalen Ansätze dann zwischen allen Teilflächen die
geometrischen Randbedingungen einhalten, um als zulässige Ansätze die Voraussetzungen
der Ritz–Gleichung (4.64) bzw. (4.65) zu erfüllen. In gleicher Weise kann man
natürlich auch bei Scheiben vorgehen.
Die geometrische Auflösung von Platten und Scheiben in Teilflächen ist beliebig. Denkbar
sind rechteckige, viereckige und dreieckige Teilflächen, die im Kontext der FEM
als finite Elemente bezeichnet werden. Die unterschiedlichen Varianten sind im
(Bild 7.1) dargestellt.
X 2
R 4
D
R 3
C D
R 2
A
A
Rand R
B
A B
1 Rand R1 B
Rand R1 Bild 7.1 : Finite Flächenelemente
– 7 / 2 –
R 3
C
R 2
R 4 R 3
C
R 2
X 1

Die geometrische und baustatische Einbindung von finiten Elementen in die Gesamt–
fläche von Platten und Scheiben erfolgt bei Recht– und Vierecken über die Ränder R 1
bis R 4 und bei Dreiecken über die Ränder R 1 bis R 3. Dazu sind auf den Rändern
Knoten zu definieren, die als Informationsträger von geometrischen und baustatischen
Daten dienen. Im Fall der Geometrie sind z.B. an den Knoten die aktuellen Werte der
X 1 – und X 2 –Koordinaten anzugeben: (X 1 , X 2 ) K , K = A, B, C und ggf. D. Geeignete
baustatische Daten sind Stützwerte von Weggrößen: Bei Platten z.B. die Stützwerte
(u 3, ϕ 1, ϕ 2) K , K = A, B, C und ggf. D von der Durchbiegung u 3 und den Verdrehungen
ϕ 1 und ϕ 2, bei Scheiben z.B. die Stützwerte (u 1, u 2) K , K = A, B, C und ggf. D von
den Verschiebungen u 1 und u 2.
Bei geradliniger Begrenzung der Ränder reichen die vier Eckknoten A, B, C und D
aus, um die Geometrie von rechteckigen oder viereckigen Teilflächen eindeutig festzulegen.
Bei Dreiecken sind dazu lediglich drei Eckknoten erforderlich, nämlich A, B und
C, vgl. (Bild 7.1). Eine benutzerfreundliche Formulierung der FEM sollte immer an–
streben, auch die baustatischen Eigenschaften der Elemente auf die Eckknoten abzubilden.
Bei modernen finiten Elementen, die auf gemischt–hybriden Ansätzen beruhen,
gelingt dies in der Regel /13/. Bei der klassischen Weggrößendarstellung /11/, /22/ und
/23/, auf die sich auch diese Einführung beschränkt, sind vielfach zusätzliche Knoten
auf den Rändern und ggf. im Elementgebiet erforderlich, um eine ausreichende Ge–
nauigkeit der baustatischen Elementlösung zu erzielen.
Die geometrische Beschreibung von Rechtecken ist besonders einfach. Die baustatische
Betrachtung wird daher auf diesen Sonderfall beschränkt. Für die praktische Anwendung
sind rechteckige Flächenelemente allerdings weniger geeignet. Die geometrische
Beschreibung von beliebigen Flächenelementen wird u.a. in der LV Vertiefung I
/13/ behandelt.
7.3 Topologie von finiten Elementen auf Flächen
Die topologische Systembeschreibung von finiten Stabelementen ist aus Statik III /12/
bekannt. Sie läßt sich in einfacher Weise auf finite Flächenelemente erweitern. Im
(Bild 7.2) sind z.B. die statischen Systeme von zwei Flächentragwerken dargestellt.
(Bild 7.2a) zeigt eine Kragscheibe und (Bild 7.2b) eine allseitig gelenkig gelagerte Platte.
Beide Systeme sind in rechteckige Teilflächen zerlegt. Der Vorgang der Elementierung
ist zunächst noch völlig unabhängig von der speziellen baustatischen Beschreibung,
die im Fall der Kragscheibe (Bild 7.2a) nach der Scheibentheorie und im Fall der allseitig
gelenkig gelagerten Platte nach der Plattentheorie erfolgen muß.
Die topologische Beschreibung erfaßt lediglich die Stellung der einzelnen Elemente
im System. Dies geschieht mit Hilfe einer unabhängigen Element– und Knotennum–
merierung, die durch eine Inzidenztafel miteinander verknüpft werden. Die Verknüpfung
ist für jedes Element anzugeben. Dazu ist die allgemeingültige Elementknotenbezeichnung
A, B, C und D im (Bild 7.1) mit den aktuellen Systemknoten im Bild (7.2) zu vergleichen
und das Ergebnis des Vergleichs unter der jeweiligen Elementnummer in eine
Tafel einzutragen.
– 7 / 3 –

L 2
a) Kragscheibe
L 2
1
X 2
21 22 23 24 25
Bild 7.2 : Elementierte Flächentragwerke
13
14 15 16
16 17 18 19 20
9 10 11 12
11 12 13 14 15
5 6 7 8
1
6 7 8 9 10
1 2 3 4
13
b) Allseitig gelenkig gelagerte Platte
2 3 4 5
L1 21 22 23 24 25
14 15 16
16 17 18 19 20
9 10 11 12
11 12 13 14 15
5 6 7 8
6 7 8 9 10
1 2 3 4
2 3 4 5
L 1
– 7 / 4 –
X 2
Knoten
Elemente
Knoten
Elemente
X 1
X 1

Die Kragscheibe (Bild 7.2a) und die allseitig gelenkig gelagerte Platte (Bild 7.2b) sind
in gleicher Weise elementiert, so daß sich für beide Systeme dieselbe Inzidenztafel ergibt,
obwohl einmal ein Scheibentragwerk und das andere Mal ein Plattentragwerk vorliegt.
Elementnummer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Elementknoten
A B C D
1 2 7 6
2 3 8 7
3 4 9 8
4 5 10 9
6 7 12 11
7 8 13 12
8 9 14 13
9 10 15 14
11 12 17 16
12 13 18 17
13 14 19 18
14 15 20 19
16 17 22 21
17 18 23 22
18 19 24 23
19 20 25 24
– 7 / 5 –
Aktuelle
Systemknoten
Die baustatischen Daten eines Flächenelements sind im Elementvektor v e enthalten.
Der Index (e) gibt die Zählvariable der Elemente an. Komponenten von v e sind entweder
die in allen Elementknoten definierten Stützwerte der Plattenweggrößen oder die
in allen Elementknoten definierten Stützwerte der Scheibenweggrößen. Im Kontext der
FEM werden die unterschiedlichen Stützwerte einheitlich als Freiwerte bezeichnet.
(7.1)

Im Systemvektor V sind die Freiwerte des elementierten Gesamtsystems zusammengestellt.
Der Zusammenhang zwischen Element– und Systemvektor ist durch
ve � BeV (7.2)
gegeben. Die Verknüpfungsmatrix B e in Gl. (7.2) ist durch die topologische Information
der Inzidenztafel Gl. (7.1) eindeutig bekannt, so daß Gl. (7.2) die baustatischen Infor–
mationen der Einzelelemente in das Gesamtsystem überträgt. Dieser Vorgang ist un–
abhängig davon, ob ein Platten– oder ein Scheibenproblem vorliegt.
7.4 Finite Plattenelemente
Aus der Vielzahl möglicher Plattenelemente soll lediglich ein schubstarres Rechteckelement
mit vier Knoten in zwei Varianten vorgestellt werden, die sich in der baustatischen
Formulierung voneinander unterscheiden. Die Konfiguration des betrachteten Elements
ist im (Bild 7.3) dargestellt.
7.4.1 Geometrie und Ansätze
Die rechteckige Elementfläche ist im (Bild 7.3a) in perspektivischer Form dargestellt.
Die dimensionslosen Ansatzkoordinaten �1 � 2 X1
s
und �
1
2 � 2 X2
s
sind in der Mitte des
2
Elements definiert und durchlaufen jeweils den Wertebereich von +1 nach –1. s1 und
s2 sind die Elementlängen in Richtung der X1 – bzw. X2 –Koordinate.
Da es sich um ein Rechteckelement handelt, verlaufen alle Ränder orthogonal zueinander.
Die Ansatzfunktionen zur bereichsweisen Auswertung der Ritz–Gleichung (4.64)
bzw. (4.65) lassen sich daher in einfacher Weise aus den Ansatzfunktionen des Biegestabs
entwickeln, wenn man die Ränder R 1 bis R 4 des Plattenelements als Biegestäbe
auffaßt. Die Biegestabansätze sind aus Statik III bekannt /12/. Entlang der Ränder R 1
bis R 4 sind sie im (Bild 7.3a) dargestellt. Die analytische Darstellung der Verlaufsfunktionen
ist (Bild 7.3b) zu entnehmen.
Die Flächenansätze des Plattenelements sind auf die Weggrößenfreiwerte der Ele–
menteckknoten zu beziehen. Dies sind jeweils die Stützwerte
�u 3 , ϕ 1 ,ϕ 2 � K , K � A, B, C und D (7.3)
der Durchbiegung u 3 und der Verdrehungen ϕ 1 = –u 3,1 und ϕ 2 = –u 3,2 , die sich bei
schubstarren Platten aus den partiellen Ableitungen der Durchbiegung ergeben. Die
Freiwerte der Eckknoten sind im (Bild 7.3a) dargestellt.
– 7 / 6 –

1
f 24
f23 1
f 22
1
Eckknoten
D(–1,+1)
1
f 21
Eckknoten
A(–1,–1)
f 12
ϕ 2A
1
f11 s 1
u 3D
ϕ2D R4 u 3A
ϕ 1A
ϕ1D R3 u 3B
a) Elementfläche, Biegestabansätze der Ränder, Freiwerte
b) Verlaufsfunktionen der Biegestabansätze
1
ϕ 1B
Bild 7.3 : Schubstarres Rechteckelement für Platten
1
1
f11 R 1
f j1 � 1
4 �1 � � j� 2 �2 � � j�
f j2 � s j
8 �1 � � j� 2 �1 � � j�
f j3 � 1
4 �1 � � j� 2 �2 � � j�
f 12
1
f13 f 14
f j4 �� s j
8 �1 � � j� 2 �1 � � j�
1
ξ 2
– 7 / 7 –
u 3C
R2 ϕ2B ϕ 1C
ξ1 ϕ2C 1
f 21
1
1
f 22
Eckknoten
B(+1,–1)
f 13
f 14
Eckknoten
C(+1,+1)
1
j = 1 → ξ 1 –Richtung
j = 2 → ξ 2 –Richtung
f23 1
1
f 24
s 2

Die Flächenansätze zur Approximation der Durchbiegungsfunktion u 3 ergeben sich
durch geeignete Kombinationen der Verlaufsfunktionen der Biegestabansätze
(Bild 7.3b). Dazu sind im Knoten A die Ansätze der Ränder R 1 und R 4, im Kno–
ten B die Ansätze der Ränder R 1 und R 2, im Knoten C die Ansätze der Ränder R 2
und R 3 und im Knoten D die Ansätze der Ränder R 3 und R 4 miteinander zu multiplizieren.
Mit den Bezeichnungen von (Bild 7.3a) erhält man für u 3 den Ausdruck
u 3 � u 3 �� 1 , � 2� (7.4)
� f 11 �� 1�f 21 �� 2�u 3A � f 12 �� 1�f 21 �� 2�ϕ 1A � f 11 �� 1�f 22 �� 2�ϕ 2A � f 12 �� 1�f 22 �� 2�ϕ 12A
� f 13 �� 1�f 21 �� 2�u 3B � f 14 �� 1�f 21 �� 2�ϕ 1B � f 13 �� 1�f 22 �� 2�ϕ 2B � f 14 �� 1�f 22 �� 2�ϕ 12B
� f 13 �� 1�f 23 �� 2�u 3C � f 14 �� 1�f 23 �� 2�ϕ 1C � f 13 �� 1�f 24 �� 2�ϕ 2C � f 14 �� 1�f 24 �� 2�ϕ 12C
� f 11 �� 1�f 23 �� 2�u 3D � f 12 �� 1�f 23 �� 2�ϕ 1D � f 11 �� 1�f 24 �� 2�ϕ 2D � f 12 �� 1�f 24 �� 2�ϕ 12D .
Die vollständige Kombination der Stabansätze ergibt nach Gl. (7.4) 16 unabhängige
Flächenansätze, für die nach Gl. (7.3) aber nur 12 physikalisch sinnvolle Weggrößenfreiwerte
der Platte existieren. Es ist daher zu diskutieren, welche physikalische Bedeutung
die Freiwerte
�ϕ 12 � K , K � A, B, C und D (7.5)
haben, die zusätzlich in Gl. (7.4) auftreten. Im einzelnen ist zu überprüfen, ob man sie
im Rahmen einer FE–Formulierung berücksichtigen muß, und wenn nein, wie eine ersatzlose
Vernachlässigung die Ergebnisse beeinflußt.
Die Flächenansätze, die zu den Freiwerten Gl. (7.5) gehören, sind in Gl. (7.4)
durch Unterstreichen gekennzeichnet. Sie entstehen durch Kombinationen der
ϕ 1– und ϕ 2–Randverläufe, die wegen der Schubstarrheit auf Ausdrücke der Form
(–u 3,1) (–u 3,2) ≡ u 3,12 führen. Die zugehörigen Freiwerte sind daher als Stützwerte der
Verwindung der Plattenmittelfläche zu deuten, die keine unmittelbaren Weggrößenfreiwerte
mehr darstellen. Diese Anteile sind aber ganz offensichtlich erforderlich, um die
geometrischen Randbedingungen zwischen benachbarten Elementen zu erfüllen, wie
es die Ritz–Gleichung (4.64) bzw. (4.65) voraussetzt.
Gl. (7.4) ist ein Ansatz, der im Elementgebiet bikubisch und auf den Elementrändern
jeweils kubisch verläuft. Auf jedem Elementrand sind die Durchbiegung u 3 und die Verdrehung
radial zum Rand ϕ r stetig zu überführen. Wegen der rechteckigen Geometrie
fallen auf den Rändern R 1 und R 3 ϕ r und ϕ 2 = –u 3,2 und auf den Rändern R 2 und
R 4 ϕ r und ϕ 1 = –u 3,1 zusammen. Pro Rand werden zur kubischen Darstellung von
u 3 vier Freiwerte benötigt, auf dem Rand R 3 z.B. die Freiwerte u 3C, u 3D, ϕ 1C und ϕ 1D,
vgl. (Bild 7.3a). Die verbleibenden Freiwerte ϕ 2C und ϕ 2D können dann ϕ r = ϕ 2 = –u 3,2
nur noch linear abbilden. Dies steht aber im direkten Widerspruch zum bikubischen Ansatz
Gl. (7.4). Auch wenn er in unvollständiger Form, d.h., ohne die unterstrichenen
Terme vorliegt, enthält er auf dem Rand R 3 in Richtung des Randes kubische Anteile
in ϕ r = ϕ 2 = –u 3,2 (Abhängigkeit von ξ 1 kubisch und von ξ 2 wegen u 3,2 quadratisch,
auf dem Rand R 3 gilt speziell ξ 1 , ξ 2 = konstant).
– 7 / 8 –

Ein Ansatz, der die unterstrichenen Terme in Gl. (7.4) vernachlässigt, führt daher zu einer
Verletzung der C 1 –Kontinuität, weil er die ersten Ableitungen von u 3 normal zu den
Plattenrändern nicht stetig überführt. Aus baustatischer Sicht liegt damit ein unvollständiger
Biegeanschluß zwischen den Elementen vor. Trotzdem liefert das nichtkonforme
Plattenelement mit 12 Freiwerten nach Gl. (7.3) akzeptable Ergebnisse. Genauer und
theoretisch abgesichert ist natürlich das Plattenelement mit 16 Freiwerten, das zusätzlich
die Verwindungsfreiwerte Gl. (7.5) enthält. Es beruht auf dem vollständigen Ansatz
Gl. (7.4) und erfüllt in strenger Weise die C 1 –Kontinuität, da es die Verdrehung normal
zum Rand nun auch durch vier Freiwerte und somit kubisch abbildet, auf dem Rand R 3
z.B. durch die Freiwerte ϕ 2C, ϕ 12C, ϕ 2D und ϕ 12D. Plattenelemente, die diese Voraussetzung
erfüllen, konvergieren stetig zur analytischen Lösung des Problems. Sie werden
als konforme Plattenelemente bezeichnet und verfügen über eine größere Anwendungssicherheit
als nichtkonforme Elemente, die ggf. zu falschen Lösungen
konvergieren können.
Die stetige Approximation mit dem bikubischen Ansatz Gl. (7.4) über die Element–
grenzen hinweg ist im (Bild 7.4) veranschaulicht. Am Beispiel des Elementver–
bands 6 , 7 , 10 und 11 aus dem Plattenbeispiel (Bild 7.2b) sind für den
Mittelknoten 13 die Verlaufsfunktionen der Freiwerte (u3, ϕ1, ϕ2, ϕ12) 13 perspektivisch
dargestellt.
Der Mittelknoten 13 wird von vier Elementknoten gebildet: Vom Eckknoten A des
Elements 11 , vom Eckknoten B des Elements 10 , vom Eckknoten C des Elements
6 und vom Eckknoten D des Elements 7 . Der biegesteife Zusammenbau der beteiligten
Elemente erfolgt durch das Gleichsetzen der zugehörigen Knotenfreiwerte.
11 10 6 7
u3A � u3B � u3C � u3D 11 10 6 7
� ϕ1B � ϕ1C � ϕ1D ϕ 1A
11 10 6 7
ϕ2A � ϕ2B � ϕ2C � ϕ2D und
11 10 6 7
ϕ12A � ϕ12B � ϕ12C � ϕ12D – 7 / 9 –
� �u 3 � 13 ,
� �ϕ 1 � 13 ,
� �ϕ 2 � 13
� �ϕ 12 � 13 .
Der stetige Übergang der Durchbiegungsfunktion u 3 (ξ 1 , ξ 2 ) längs der gemeinsamen
Elementränder (12, 13, 14) und (8, 13, 17) ist dann durch die Verlaufsfunktionen der
Freiwerte (u 3) 13 (Bild 7.4a), (ϕ 1) 13 (Bild 7.4b) und (ϕ 2) 13 (Bild 7.4c) gegeben. Damit
ist aber zunächst nur die C 0 –Kontinuität gesichert, die sich allein auf den Funktionswert
von u 3 (ξ 1 , ξ 2 ) bezieht. Die volle C 1 –Kontinuität, die auch den stetigen Übergang der
ersten Ableitungen u 3,1 und u 3,2 von u 3 (ξ 1 , ξ 2 ) einschließt, kann dagegen nur erreicht
werden, wenn man zusätzlich die Verlaufsfunktion des Verwindungsfreiwerts (ϕ 12) 13
(Bild 7.4d) einbezieht, um damit die Änderung von u 3,1 in X 2 –Richtung und von u 3,2
in X 1 –Richtung zu erfassen.

a) Freiwert (u 3) 13 der Durchbiegung u 3
b) Freiwert (ϕ 1) 13 der Verdrehung ϕ 1 = –u 3,1
c) Freiwert (ϕ 2) 13 der Verdrehung ϕ 2 = –u 3,2
d) Freiwert (ϕ 12) 13 der Verwindung u 3,12
Bild 7.4 :
f 13(ξ 1 ) f 21(ξ 2 )
f 13(ξ 1 ) f 23(ξ 2 )
12
6
7 8 9
6 7
7 8 9
6
7 8 9
– 7 / 10 –
X 2 ,ξ 2
17 18 19
(u
10
3) 13
11
1
17 18 19
17
10
18 19
11
13
12 (ϕ2) 13 14
1
17 18 19
10
(ϕ 12) 13
12 14
13
7
Verlaufsfunktionen der Plattenfreiwerte im Elementverband
13
11
X 1 ,ξ 1
f14(ξ 10
1
(ϕ1) 13
11
14
12
6
13 1
7
7 8 9
1 ) f21(ξ2 )
f12(ξ1 ) f21(ξ2 )
f14(ξ1 ) f23(ξ2 )
f12(ξ1 ) f23(ξ2 )
f 13(ξ 1 ) f 22(ξ 2 )
f 13(ξ 1 ) f 24(ξ 2 )
f 14(ξ 1 ) f 22(ξ 2 )
f 14(ξ 1 ) f 24(ξ 2 )
1
7
14
f 11(ξ 1 ) f 23(ξ 2 )
f 11(ξ 1 ) f 22(ξ 2 )
f 11(ξ 1 ) f 21(ξ 2 )
f 11(ξ 1 ) f 22(ξ 2 )
f 12(ξ 1 ) f 22(ξ 2 )
f 12(ξ 1 ) f 24(ξ 2 )

7.4.2 Diskretisierung auf Element– und Systemebene
Beim klassischen Ritz–Verfahren der Plattentheorie mit Gesamtansätzen verwendet
man in der Regel das Prinzip vom Minimum der potentiellen Energie Gl. (4.65), um die
unbekannten Konstanten der Ansätze zu ermitteln. Im Rahmen der FEM ist es dagegen
üblich, unmittelbar auf das PvW Gl. (4.64) zurückzugreifen.
Das Ausschreiben von Gl. (4.64) unter Beachtung von Gl. (4.23.2) ergibt die analytische
Matrizengleichung
�W � � G
�� G
��u3,11 ,u3,22 ,2u � 3,12 0 1
1
– 7 / 11 –
�
0
(B 0
) dG
0 0
1 � �
2
u 3,11
u 3,22
2u 3,12
�u 3 p 3 dG � 0 . (7.6)
Die Diskretisierung von Gl. (7.6) ist ein rein technischer Vorgang. Zunächst ist der Ansatz
Gl. (7.4) in Gl. (7.6) einzusetzen. Dabei sind die partiellen Ableitungen u 3,11 , u 3,22
und u 3,12 unter Beachtung der Kettenregel zu entwickeln. Dann ist die Integration
durchzuführen. Dies kann im vorliegenden Fall wegen der einfachen Elementgeometrie
sogar noch in analytisch geschlossener Form erfolgen. Danach ist das Ergebnis in Form
einer diskreten Matrizengleichung zu ordnen. Dazu wird der Elementvektor
v e � {u 3A ϕ 1A ϕ 2A ϕ 12A | u 3B ϕ 1B ϕ 2B ϕ 12B |
u 3C ϕ 1C ϕ 2C ϕ 12C | u 3D ϕ 1D ϕ 2D ϕ 12D }
(7.7)
eingeführt, der die unbekannten Elementfreiwerte Gl. (7.3) und Gl. (7.5) der konformen
Elementvariante in der Reihenfolge der Eckknoten auflistet. Bei der nichtkonformen
Elementvariante entfallen die Verwindungsfreiwerte ϕ 12A, ϕ 12B, ϕ 12C und ϕ 12D . Mit
Gl. (7.7) erhält man für die Kurzform der diskreten Matrizengleichung den Ausdruck
�W e � ��v T�kv � s 0�� e � 0 . (7.8)
In Gl. (7.8) bezeichnet k e die Steifigkeitsmatrix und s 0 e die Einwirkungsmatrix des
e–ten Plattenelements. Die Übertragung ins System geschieht mit Hilfe von Gl. (7.2).
�We � �V T��B T kB� e V � �B T s 0� e � � 0. (7.9)
Die Summe über alle Elemente ergibt die Systemgleichung des PvW für ein elementiertes
Plattensystem.
�W � � �We � �V T�KV � S 0� e � 0. (7.10)

In Gl. (7.10) bezeichnet
K � ��B T kB� e
die System–Steifigkeitsmatrix und
S 0 � ��B T s 0� e
– 7 / 12 –
(7.10.1)
(7.10.2)
die System–Einwirkungsmatrix. Nach dem Einarbeiten der aktuellen geometrischen
Randbedingungen sind durch die Lösung des Gleichungssystems
KV� S 0 � V (7.11)
alle Weggrößenfreiwerte der Systemknoten bekannt. Durch eine elementweise Nachlaufrechnung
können dann die Momente und ggf. auch die Querkräfte und Verdrehungen
ermittelt werden, so daß eine vollständige Lösung des Plattenproblems vorliegt.
7.4.3 Überprüfung der Konvergenz
Anhand der allseitig gelenkig gelagerten Quadratplatte L 1 = L 2 = a (Bild 4.9) und einer
Elementierung gemäß (Bild 7.2b) soll das Konvergenzverhalten des schubstarren Plattenelements
(Bild 7.3) für die Lastfälle LF1: Vollast p 3 = konstant und LF2: Einzel–
last F in Plattenmitte überprüft werden. Wegen der Symmetrie kann sich die Elementierung
auf ein Viertel der Plattenfläche beschränken. Für die spezielle Netzteilung n = 2×2
ist sie im (Bild 7.5) dargestellt.
a/2
u 3 = 0
1
ϕ 2 = 0
7 8 9
3 4
4 5 6
1 2
u3 = 0
a/2
2 3
Bild 7.5 : Netzteilung einer Quadratplatte
X 2
X 1
ϕ 1 = 0
Die Freiwerte der Durchbiegung u 3 sind in den Randknoten auf Null zu setzen, um die
geometrischen Randbedingungen der gelenkig gelagerten Platte zu erfüllen. In den

Knoten auf der Symmetrielinie (X 1 = 0, X 2 ) sind die Freiwerte der Verdrehung ϕ 1 und
in den Knoten auf der Symmetrielinie (X 1 , X 2 = 0) sind die Freiwerte der Verdrehung
ϕ 2 auf Null zu setzen, um die Symmetriebedingungen in Plattenmitte zu erfassen.
Die Berechnungen werden mit der nichtkonformen (12 Freiwerte) und der konformen
Elementvariante (16 Freiwerte) durchgeführt. Einflußparameter ist die Netzteilung
n = 1×1, n = 2×2, n = 4×4 und n = 8×8. Die Ergebnisse der Mittendurchbiegung sind
im (Bild 7.6) in Form von Konvergenzkurven dargestellt.
20%
15%
10%
5%
0
–5%
–10%
–15%
Ç
Ç
Ç
–20%
1×1
Bild 7.6 :
Fehler f �� �
�
uFEM � uAnalytisch
3M 3M
aAnalytisch 3M
ÇÇ
ÇÇ
Ç
Ç
�
�
� 100%
ÇÇ
ÇÇ
Ç
Ç
– 7 / 13 –
Ç
Ç
2×2 4×4 8×8
Konformes Element mit 16 Freiwerten
LF1 : Vollast p3 LF2 : Einzellast F in Plattenmitte
Nichtkonformes Element mit 12 Freiwerten
LF1 : Vollast p3 LF2 : Einzellast F in Plattenmitte
Netzteilung
Konvergenzkurven der Mittendurchbiegung einer allseitig
gelenkig gelagerten Quadratplatte

Die analytische Lösung ist durch den minimalen Wert der potentiellen Gesamtenergie
gekennzeichnet. Der zugehörige Steifigkeitszustand des Plattensystems stellt eine untere
Grenze dar, die man nicht unterschreiten kann. Weggrößenelemente müssen daher
von der steifen Seite konvergieren, so daß die Freiwerte mit zunehmender Netz–
teilung anwachsen. Diese Betrachtung gilt aber nur für konforme Elemente. Für den
Lastfall 2: Einzellast F in Plattenmitte trifft sie auch zu, für den Lastfall 1: Vollast p 3
dagegen nicht. Der Grund hierfür liegt in der Approximation der Flächenlast durch das
Integral der äußeren Arbeit. Dadurch wird die Flächenlast in äquivalente Knotenlasten
umgewandelt, die eine obere Grenze der Flächenlast darstellen, so daß im vorliegenden
Fall wegen der überschätzten Einwirkung die Approximation von der zu weichen
Seite aus erfolgt.
Für das nichtkonforme Element kann man hinsichtlich des Konvergenzverhaltens keine
eindeutige Aussage treffen. Beim Lastfall 1: Vollast p 3 erfolgt die Approximation von
der steifen Seite, beim Lastfall 2: Einzellast F in Plattenmitte dagegen von der weichen
Seite. Insgesamt ist aber festzustellen, daß beide Elementvarianten sehr gut konvergieren.
7.4.4 Einfaches Anwendungsbeispiel
Im (Bild 7.7) ist das statische System einer Rechteckplatte aus Stahlbeton dargestellt.
Die freie Spannweite in Längsrichtung (X 1 –Koordinate) erstreckt sich über 16. m und
in Querrichtung (X 2 –Koordinate) über 8. m. Die beiden Längsränder sind fest einge–
spannt und die beiden Querränder gelenkig gelagert. Die Querdehnzahl beträgt ν = 0.2.
Die Biegesteifigkeit und die Flächenlast für den Lastfall Vollast werden als Einheitswerte
angegeben: B = 1. (kN/m 2) /m und p 3 = –1. (kN/m 2 ). Die Zustandsgrößen (u 3,
m 11 und m 22 ) sind mit Hilfe einer FEM–Berechnung zu ermitteln und in Plattenmitte
im Längs– und Querschnitt darzustellen.
Wegen der Doppelsymmetrie ist nur ein Viertel des Systems zu elementieren. Auf den
Symmetrielinien sind die Freiwerte der Verdrehungen zu sperren: Auf X 1 = 0 gilt
ϕ 1 = 0 und auf X 2 = 0 gilt ϕ 2 = 0. Auf dem gelenkig gelagerten Rand sind die Frei–
werte der Durchbiegung und auf dem eingespannten Rand sind die Freiwerte der
Durchbiegung und der Verdrehung radial zum Rand zu sperren: Auf X 1 = 8. m gilt
u 3 = 0 und auf X 2 = 4. m gilt u 3 = 0 und ϕ r = ϕ 2 = 0. Eine analytische Lösung ist nicht
bekannt. Die Vergleichslösung wird daher mit einer 16×8 Netzteilung der Längs– und
Querrichtung ermittelt, die auf einer quadratischen 0.5×0.5 m 2 Elementierung mit dem
konformen Rechteckelement beruht, das 16 Freiwerte enthält.
– 7 / 14 –

X 3 ,u 3
p 3
8.
4.
4.
Bild 7.7 : Anwendungsbeispiel
ϕ 1 = 0
ν = 0.2
B = 1. (kN/m 2) /m
p 3 = –1. (kN/m)
– 7 / 15 –
X 2
8. 8.
16. m
X 3 ,u 3
ϕ2 = 0 2×4
u3 = 0
Netzteilung
ϕ 2 = 0
p 3
u 3 = 0
Eine Berechnung mit einer 4×2 Netzteilung mit demselbem Element ergibt bereits eine
sehr gute Übereinstimmung mit der Vergleichslösung. Die Lösung des nichtkonformen
Elements, das nur 12 Freiwerte enthält, unterscheidet sich bei dieser Netzteilung nur
geringfügig von der Lösung des höherwertigen konformen Elements.
Die Ergebnisse der Berechnungen sind in der Mitte der Platte ausgewertet. Im (Bild 7.8)
sind die Verläufe von (u 3, m 11 und m 22 ) im Längsschnitt und im (Bild 7.9) im Querschnitt
dargestellt. Qualitativ stimmen sie mit den Verläufen überein, die man von den
zugeordneten Biegebalken der Längs– und Querrichtung erwartet. Lediglich die Verteilung
des m 11 –Moments des gelenkig gelagerten Längsbalkens im (Bild 7.8b) weicht
von dieser Erwartung ab, weil sich durch den Platteneffekt der Maximalwert nicht wie
beim Biegebalken in der Mitte sondern im Randbereich einstellt. Die Größenordnung
der Zahlen kann man mit den Czerny–Tabellen /20/ überprüfen, die für den Sonderfall
ν = 0 gelten. Diese Werte sind zusätzlich in den (Bildern 7.8 und 7.9) angegeben. In
den eingespannten Längsrändern muß sich wegen der dort geltenden kinematischen
Bedingung � K 11 � 0 das Momentenverhältnis m11 = νm 22 einstellen. Ein Blick auf
(Bild 7.9b und c) zeigt, daß die FE–Berechnungen diese Bedingung erfüllen.
X 1

Mitte
–10.2880
–10.8380
–10.7162
–10.6837
a) Durchbiegung u 3
–0.6417
–0.6780
–0.7020
b) Moment m 11
–2.7073
–3.0520
–3.0120
–2.6556
c) Moment m 22
u3
� p 3
� p 3
� p 3
–
–
m 22
–
m 11
–8.9718
–9.4745
–9.2237
–0.9647
–1.0600
–1.0305
–2.3842
–2.6700
–2.6012
Bild 7.8 : Zustandsgrößen im Längsschnitt der Plattenmitte (X 1 ,X 2 = 0), vgl. (Bild 7.7)
– 7 / 16 –
Bu 3 (kN/m 2 )
Gelenkig
gelagerter Rand
Vergleichslösung
2×4 12
2×4 16
Czerny /20/
m 11 (kNm/m)
m 22 (kNm/m)

Mitte
–10.2880
–10.8380
–10.7162
–10.6837
Bu 3 (kN/m 2 )
a) Durchbiegung u3 m11 (kNm/m)
b) Moment m 11
–0.6417
–0.6780
–0.7020
–
–
m 22 (kNm/m)
–
–0.1926
–0.2402
–0.2581
Vergleichslösung
2×4 12
2×6 12
Czerny /20/
Bild 7.9 : Zustandsgrößen im Querschnitt der Plattenmitte (X 1 = 0, X 2 ), vgl. (Bild 7.7)
– 7 / 17 –
Eingespannter
Rand
1.0757
1.0200
1.0140
c) Moment m22 –2.7073
–0.7157
5.3786
–3.0520
–1.030
5.0220
–3.0120
–1.026
5.0710
–2.6556 5.3339
+
+
u3
� p 3
� p 3
� p 3
m 22
m 11

7.5 Finite Scheibenelemente
Aus der Vielzahl möglicher Scheibenelemente wird lediglich ein Rechteckelement mit
vier Knoten vorgestellt. Die Konfiguration des betrachteten Elements ist (Bild 7.10) zu
entnehmen. Grundlage der Elementbeschreibung ist die Differentialgleichung (3.34),
die das Gleichgewicht von Scheiben durch eine Weggrößenformulierung ausdrückt.
Die Ableitung der zugehörigen Arbeitsgleichung mit dem PvW ist in gleicher Weise wie
beim Plattenproblem vorzunehmen, vgl. Teil 4, Abschnitt 4.6.2: Ritz–Verfahren. Als Ergebnis
erhält man den Ausdruck
�W � � �u �,� �DE �����u �,� dG �� �u�p � dG � 0. (7.12)
Gl. (7.12) muß als Zwangsbedingungen die geometrischen Randbedingungen der Verschiebungen
Gl. (3.32.1) erfüllen, deren Komponenten radial und tangential zu den Elementrändern
wirken. Die geometrischen Randbedingungen gelten auch für die virtuellen
Verschiebungen. Die statischen Randbedingungen der radialen und tangentialen
Randkräfte Gl. (3.32.2) unterliegen dagegen keinen Zwängen. Sie sind implizit als natürliche
Bedingungen in Gl. (7.12) enthalten.
7.5.1 Geometrie und Ansätze
Die Geometrie des Scheibenelements (Bild 7.10) stimmt vollständig mit der Geometrie
des Plattenelements (Bild 7.3) überein. In der baustatischen Beschreibung ergeben
sich dagegen Unterschiede. Die Differentialgleichung des Scheibenproblems Gl. (3.34)
ist von zweiter Ordnung, während mit der Plattengleichung (4.39) ein Problem von vierter
Ordnung vorliegt. Deswegen treten in der zugehörigen schwachen Form des Scheibenproblems
Gl. (7.12) nur erste Ableitungen auf. Ansätze zur Approximation der Verschiebungen
u 1 und u 2 müssen daher nur die C°–Kontinuität erfüllen. Dies reicht
bereits aus, um konforme Scheibenelemente zu erhalten, die sich stetig in die Umgebung
einpassen.
Faßt man die Elementränder als Dehnstäbe auf, so kann man die Konstruktion von
zulässigen Ansätzen in einfacher Weise mit den aus Statik III /12/ bekannten linea–
ren Verlaufsfunktionen für Dehnstäbe durchführen. Entlang der Ränder R 1 bis R 4 sind
die Verlaufsfunktionen im (Bild 7.10a) dargestellt. Die analytische Darstellung ist
(Bild 7.10b) zu entnehmen.
– 7 / 18 –

f 12(ξ 1 ) f 21(ξ 2 )
f 12(ξ 1 ) f 22(ξ 2 )
f22 1
1
f 21
Eckknoten
A(–1,–1)
Eckknoten
D(–1,+1)
u 1A
1
f11 a) Elementfläche, Dehnstabansätze der Ränder, Freiwerte
f j1 � 1
2 �1 � � j�
f j2 � 1
2 �1 � � j�
b) Verlaufsfunktionen der Dehnstabansätze
12
u 1D
R 4
u 2A
X2 ,ξ2 17 18 19
10
6
1
f11 u2D R3 1 (u 2) 13
7 8 9
c) Verlaufsfunktion der Scheibenfreiwerte im Elementverband
R 1
Bild 7.10 : Rechteckelement für Scheiben
1
f 12
13
ξ 2
u 2B
7
– 7 / 19 –
R2 u1B ξ1 u1C f 21
1
f12 j = 1 → ξ 1 –Richtung
j = 2 → ξ 2 –Richtung
(u 1) 13
u 2C
1
Eckknoten
B(+1,–1)
14
Eckknoten
C(+1,+1)
11
f 22
1
f 11(ξ 1 ) f 22(ξ 2 )
f 11(ξ 1 ) f 21(ξ 2 )
X 1 ,ξ 1

Die Kombination der Stabansätze ergibt den Flächenansatz
u� � u� �� 1 , � 2�
� f 11 �� 1�f 21 �� 2�u �A � f 12 �� 1�f 21 �� 2�u �B � f 12 �� 1�f 22 �� 2�u �C � f 11 �� 1�f 22 �� 2�u �D ,
– 7 / 20 –
(7.13)
der mit α = 1, 2 für beide Scheibenrichtungen gilt. Freiwerte des Ansatzes Gl. (7.13)
sind die Stützwerte der Verschiebungen u 1 und u 2 in den Eckknoten.
�u 1 ,u 2 � K , K � A, B, C und D . (7.14)
Gl. (7.13) ist ein Ansatz, der im Elementgebiet bilinear und auf den Elementrändern
linear verläuft. Auf den Elementrändern sind die radiale und tangentiale Verschiebung
u r und u t stetig zu überführen. Dazu sind pro Rand und Verschiebungsrichtung jeweils
zwei Freiwerte erforderlich. Sie sind durch Gl. (7.14) eindeutig definiert, so daß mit
Gl. (7.13) ein konformer Flächenansatz für Scheibenelemente vorliegt. Am Beispiel des
Elementverbands 6 , 7 , 10 und 11 aus dem Scheibenbeispiel (Bild 7.2a) ist
die stetige Approximation über die Elementgrenzen hinweg im (Bild 7.10c) veranschaulicht.
7.5.2 Diskretisierung
Das Ausschreiben von Gl. (7.12) unter Beachtung von Gl. (3.24.1) ergibt die analytische
Matrizengleichung
�W � � G
�� G
��u1,1 ,u2,2 ,u1,2 � u � 2,1 ν 1
��u 1 u 2 �� p1
1
�
0
(D 0
) dG
0 0
1 � �
2
u 1,1
u 2,2
u 1,2 + u 2,1
p 2� dG � 0 . (7.15)
Die Diskretisierung von Gl. (7.15) ist auch beim Scheibenelement ein rein technischer
Vorgang. Dazu ist der Ansatz Gl. (7.13) in Gl. (7.15) einzusetzen und das Ergebnis in
Form der diskreten Matrizengleichung (7.8) zu ordnen. Zum Aufbau von Gl. (7.8) ist der
Elementvektor
v e � �u 1A u 2A | u 1B u 2B | u 1C u 2C | u 1D u 2D � . (7.16)
einzuführen, der die unbekannten Freiwerte des Scheibenelements Gl. (7.14) in Reihenfolge
der Eckknoten auflistet. Damit ist die Elementbeschreibung abgeschlossen.
Die Beschreibung auf Systemebene erfolgt analog zur Vorgehensweise beim Platten–
element. Weitere Ausführungen sind daher nicht erforderlich.

7.5.3 Überprüfung der Konvergenz
Das vorgestellte einfache Rechteckelement mit vier Eckknoten und jeweils zwei Verschiebungsfreiwerten
in den Knoten konvergiert für Scheibenlösungen ohne Biegeanteil
relativ gut. Ein solcher Fall liegt z.B. vor, wenn auf dem freien Rand X 1 = L 1 der Kragscheibe
im (Bild 7.2a) Lasten in X 1 –Richtung einwirken. Verläuft die Wirkungslinie der
Randlasten dagegen in Richtung der X 2 –Koordinate, liegt ein Biegeproblem vor. In
diesem Fall nimmt die Konvergenzgeschwindigkeit deutlich ab. Wegen des linearen
Verschiebungsansatzes ist das Element nicht in der Lage, Biegeverformungen in
vollständiger Form zu approximieren. Dieser Sachverhalt ist im (Bild 7.11) dargestellt.
(Bild 7.11a) zeigt die Sollform der Biegung, die sich unter einer Momenteneinwirkung
einstellt und (Bild 7.11b) die Approximation durch das finite Scheibenelement. Es sind
keine u 2–Verschiebungen im Elementbereich aktiviert. Eine Biegung kann das Element
daher nur unvollständig abbilden. In der Regel sind eine Vielzahl von Elementen vor
allem in Längsrichtung der Biegung erforderlich, um auf Systemebene brauchbare
Ergebnisse zu erzielen.
M
a) Sollform b) Approximation
Bild 7.11 : Biegeverformung bei einfachen Scheibenelementen
– 7 / 21 –
u 1A
u 1D
X 2 , u 2
u 1C
D C
M M M
A B
u 1B
X 1 , u 1
Dies soll am Beispiel des statisch bestimmten Biegebalkens unter einer mittigen Einzellast
verdeutlicht werden. Wegen der Symmetrie ist nur das halbe System zu elementieren.
Die spezielle 1×5 Elementierung mit einem Element in Richtung der Balkenhöhe
und fünf Elementen in Längsrichtung ist im (Bild 7.12) dargestellt.

2
1
X 2 , u 2
Bild 7.12 : Biegebalken
4
– 7 / 22 –
(u 1) 12 = 0
1 2 3 4 5
1.0
3
6 8
10 12
5 7
(u2) 1 = 0
1 1 1 1 1
s/2 = 10/2 = 5 m
9
11
F/2 = 1000/2 = 500 kN
X 1 , u 1
(u 1) 11 = 0
E � 2.110 7 kN�m 2
� � 0.2
0.50
Neben der 1×5 Elementierung kommen noch die Elementierungen 2×10 und 4×20
zur Anwendung, um die Konvergenz der Mittendurchbiegung des Biegebalkens abzuschätzen.
Die Scheibenelemente enthalten den Einfluß der Querkraftverformungen.
Bei der analytischen Vergleichslösung des Biegebalkens ist dieser Einfluß daher zusätzlich
zu berücksichtigen
w A � 1
48
Fs 3
EI
� 1
4
Fs
GA Q
.
Der Schubmodul ist durch G �
E
2(1 � �) und die Schubfläche durch AQ kannt. Die Zahlenberechnung ergibt den Vergleichswert
w A � (2.38 � 0.07)10 �2 m � 2.45 cm .
�
5
A be-
6
Die Ergebnisse der FE–Berechnungen sind (Tabelle 7.1) zu entnehmen. Angegeben
ist jeweils der Mittelwert
w FEM � �� ��
��
�
�
�u � 2 � �u �
12 2 11
2
der vertikalen Scheibenverschiebungen in Balkenmitte und der Fehler
f � w A � w FEM
w A
in Bezug auf den analytisch ermittelten Vergleichswert.

Typ
Weggrößen–
Element
Netz
Gemischt–hybrides
Element /13/
1×5 2×10 4×20
w FEM (cm) f (%) w FEM (cm) f (%) w FEM (cm) f (%)
1.67
2.41
31.8
1.6
Tabelle 7.1 : Ergebnisse der Konvergenzuntersuchung für Scheibenelemente
– 7 / 23 –
2.18
2.43
11.0
0.8
2.37
2.45
Das Weggrößenelement konvergiert wie erwartet sehr langsam. Der Defekt in der
Biegeapproximation wirkt sich besonders bei wenigen Elementen sehr stark aus. Das
zusätzlich in den Vergleich einbezogene gemischt–hybride Scheibenelement, das auf
Systemebene die gleiche Konfiguration wie das Weggrößenelement aufweist, nämlich
vier Eckknoten mit jeweils zwei Verschiebungsfreiwerten, konvergiert dagegen deutlich
schneller, weil die gemischt–hybride Formulierung in der Lage ist, den Defekt in der Biegeapproximation
auf Elementebene durch den Ansatz von unabhängigen Kraftgrößen
zu beheben. Eine detailierte Beschreibung von gemischt–hybriden Elementen wird in
/13/ vorgestellt.
7.5.4 Anwendungsbeispiel
Wandscheiben aus Stahlbeton sind ein vielfach verwendetes Konstruktionselement im
Ingenieurhochbau. Ein wichtiger Konstruktionsparameter, der das Tragverhalten stark
beeinflußt, ist die Wandhöhe. Im Rahmen einer Fallstudie soll dieser Einfluß untersucht
werden.
Das statische System im (Bild 7.13) weist daher bei fester Spannweite L = 10. m eine
variable Wandhöhe H i auf. Die FE–Berechnung erfolgt mit i = 1, 2, 3 speziellen Wandhöhen,
die drei charakteristische Tragwerke darstellen:
1. H 1 = 2.50 m → Biegebalken.
2. H 2 = 10.00 m → Quadratscheibe.
3. H 3 = 15.00 m → Rechteckscheibe.
Die Genauigkeit des in Abschnitt 7.5.1 vorgestellten Weggrößenelements ist vor allem
bei Biegeproblemen gering, vgl. (Tabelle 7.1). Die Berechnungen werden daher mit dem
FE–Programm GEMAS /13/ durchgeführt, um die erhöhte Genauigkeit von gemischt–
hybriden Scheibenelementen bei Anwendungen auf Biegeproblemen zu nutzen.
3.3
0.

X 2 , u 2
E � 310 7 kN�m 2
� � 0.2
5. 5.
L = 10. m
F = 1000 kN
Bild 7.13 : Statisches System einer Wandscheibe mit variabler Höhe
– 7 / 24 –
X 1 , u 1
t = 0.40 m
Die Elementierung mit variabler Wandhöhe beruht auf quadratischen Elementen mit
fester Seitenlänge, die immer 0.5 m beträgt. Sie erfolgt wegen der unsymmetrischen
Lagerung jeweils für das ganze System. Für die einzelnen Systeme ergeben sich unterschiedliche
Längen × Höhen–Netzteilungen: Beim Biegebalken beträgt sie 20×5 , bei
der Quadratscheibe 20×20 und bei der Rechteckscheibe 20×30. Die Einzellast wird
anteilig auf drei benachbarte Knoten verteilt, die jeweils eine Elementlänge auseinander
liegen.
Die Ergebnisauswertung ist in den (Bildern 7.14, 7.15 und 7.16) dargestellt. Den
Lastabtrag in Scheiben kann man sehr gut aus dem Verlauf der Hauptkräfte erkennen.
Sie sind als Druck– und Zugtrajektorien veranschaulicht. Zusätzlich sind die Verläufe
der Längskräfte n 11 und n 22 im Vertikalschnitt in der Mitte der Scheibe ausgewertet.
Dies geschieht bei gemischt–hybriden Formulierungen in der Mitte der Elemente. Die
Schnitte beginnen daher in der Mitte des unteren Elements und enden in der Mitte des
oberen Elements.
Beim Biegebalken (Bild 7.14) ist die Ausbildung der Trajektorien in Druck– und Zug–
bögen sehr gut zu erkennen (Bild 7.14a). Lediglich im Bereich der Lasteinleitung und
der Auflager treten Störungen auf. Bei 2.50 m Balkenhöhe und 10.0 m Spannweite
gilt L/H = 4. Die Voraussetzung der Bernoulli–Hypothese vom Ebenbleiben der Querschnitte
ist erfüllt. Die Längskraft n 11 im (Bild 7.14b) ist daher geradlinig im Querschnitt
verteilt. Die geringfügige Abweichung im oberen Bereich resultiert aus der Lastein–
leitung. Eine Abschätzung der Größenordnung von n 11 ist in einfacher Weise möglich.
Das Balkenmoment in der Mitte berechnet sich unter Betrachtung der Lastverteilung zu
M = 500⋅5 – 250⋅0.5 = 2375. kNm. Das Trägheitsmoment der Querschnittshöhe beträgt
H i

I = 2.5 3 /12 = 1.3 m 3 . Der betrachtete Punkt am unteren Rand liegt in Z = 2.50/2 – 0.25
= 1.0 m Entfernung von der Stabachse. Die Auswertung n 11 = (M/I)⋅Z ergibt den Wert
n 11 = (2375/1.3)⋅1 = 1824. kN/m, der mit den Zahlenangaben im (Bild 7.14b) übereinstimmt.
a) Trajektorien
2.10+03
1.40+03
7.00+02
0.
–7.00+02
–1.40+03
–2.10+03
Bild 7.14 : Biegebalken
0. 4.00–01 8.00–01 1.20+00 1.60+00 2.00+00 2.40+00
b) Verteilung der Längskräfte in der Mitte
Im Verlauf der Trajektorien der Quadratscheibe (Bild 7.15) kann man sehr gut das statische
System eines Dreiblocks erkennen (Bild 7.15a). Die Druckstreben verlaufen von
der Last zum linken und rechten Auflager, während sich das Zugband zwischen den
Auflagern parallel zum unteren Rand ausbildet. Bei 10.0 m Scheibenhöhe und 10.0 m
Spannweite gilt L/H = 1. Für diese Abmessungen trifft die Bernoulli–Hypothese nicht
mehr zu. Die Balkenlösung erfüllt zwar noch das Gleichgewicht, verletzt aber die
Verträglichkeit der Scheibe. Der Verlauf der Längskraft n 11 im vertikalen Mittenschnitt
(Bild 7.15b) weicht daher stark von der geradlinigen Verteilung der Balkentheorie ab.
– 7 / 25 –
n 11
n 22

a) Trajektorien
2.50+02
0.
–2.50+02
–5.00+02
–7.50+02
–1.00+03
–1.25+03
Bild 7.15 : Quadratscheibe
0. 2.00+00 4.00+00 6.00+00 8.00+00 1.00+01 1.20+01
b) Verteilung der Längskräfte in der Mitte
– 7 / 26 –
n 11
n 22

Bei der 15.0 m hohen Rechteckscheibe (Bild 7.16) gilt das Verhältnis L/H = 0.666.
Der Verlauf der Trajektorien ist im (Bild 7.16a) und die Verteilung der Längskräfte im
(Bild 7.16b) dargestellt. Im direkten Vergleich zur Quadratscheibe sind nur geringfügige
Änderungen zu erkennen.
Bei der Quadrat– und Rechteckscheibe gelingt es nicht mehr, in einer ersten
Näherung mit Hilfe der Balkentheorie die Größenordnung der Gleichgewichtskraft n 11
abzuschätzen. Am oberen und unteren Rand erhält man aus n 11 = (M/I)⋅Z bei der
Quadratscheibe den Wert n 11 = �1350 kN/m und bei der Rechteckscheibe den Wert
n 11 = �61. kN/m. Ein Vergleich mit den (Bildern 7.15b und 7.16b) zeigt, daß die Kräfte,
die sich aus der Scheibenberechnung ergeben, deutlich größer ausfallen. Sie erreichen
am oberen Rand jeweils den Wert n 11 � –500. kN/m (Druck) und am unteren Rand jeweils
den Wert n 11 � 200. kN/m (Zug). Eine Bemessung des Zugbereichs auf der
Grundlage der Balkentheorie muß daher zu einer unkontrollierten Rißbildung führen,
die ggf. die Gebrauchstauglichkeit der Scheiben einschränken kann.
– 7 / 27 –

a) Trajektorien
2.50+02
0.
–2.50+02
–5.00+02
–7.50+02
–1.00+03
–1.25+03
0. 2.50+00 5.00+00 7.50+00 1.00+01 1.25+01 1.50+01
b) Verteilung der Längskräfte in der Mitte
Bild 7.16 : Rechteckscheibe
n 11
n 22
– 7 / 28 –