Curved Beam - VTU e-Learning

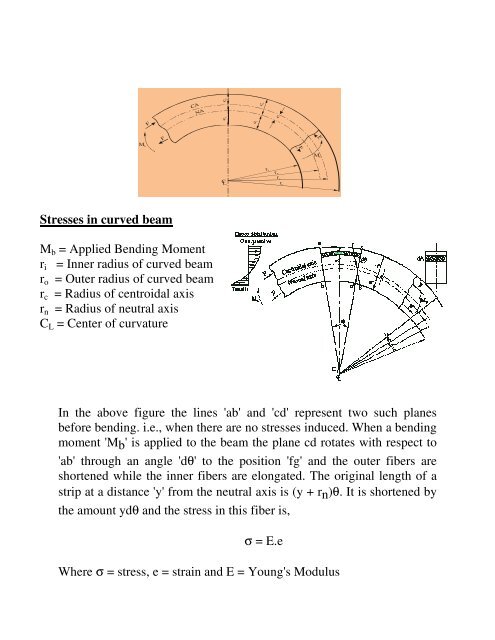
Stresses in curved beam
Mb = Applied Bending Moment
ri = Inner radius of curved beam
ro = Outer radius of curved beam
rc = Radius of centroidal axis
rn = Radius of neutral axis
CL = Center of curvature
M b
F
F
In the above figure the lines 'ab' and 'cd' represent two such planes
before bending. i.e., when there are no stresses induced. When a bending
moment 'Mb' ' is applied to the beam the plane cd rotates with respect to
'ab' through an angle 'd 'dθ' ' to the position 'fg' and the outer fibers are
shortened while the inner fibers s are elongated. The original length of a
strip at a distance 'y' from the neutral axis is (y + rrn)θ.
It is shortened by
the amount ydθ and the stress in this fiber is,
NA c 2
CA
σ = E.e
Where σ = stress, e = strain and E = Young's Modulus
c 1
C L
c i c o
r i
e
r n
r c
r o
F
F
M b