Spatial Characterization Of Two-Photon States - GAP-Optique

Signal
purity
1
0
(a)
0.1 3
2.3. Correlations between signal and idler
(b)
0.1 Pump waist 3
(c)
0.1
Emission
angle
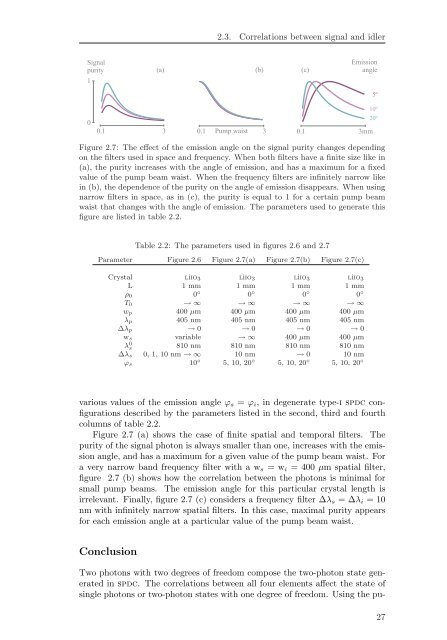
Figure 2.7: The effect of the emission angle on the signal purity changes depending
on the filters used in space and frequency. When both filters have a finite size like in
(a), the purity increases with the angle of emission, and has a maximum for a fixed
value of the pump beam waist. When the frequency filters are infinitely narrow like
in (b), the dependence of the purity on the angle of emission disappears. When using
narrow filters in space, as in (c), the purity is equal to 1 for a certain pump beam
waist that changes with the angle of emission. The parameters used to generate this
figure are listed in table 2.2.
Table 2.2: The parameters used in figures 2.6 and 2.7
Parameter Figure 2.6 Figure 2.7(a) Figure 2.7(b) Figure 2.7(c)
Crystal liio3 liio3 liio3 liio3
L 1 mm 1 mm 1 mm 1 mm
ρ0 0 ◦ 0 ◦ 0 ◦ 0 ◦
T0 → ∞ → ∞ → ∞ → ∞
wp 400 µm 400 µm 400 µm 400 µm
λp 405 nm 405 nm 405 nm 405 nm
∆λp → 0 → 0 → 0 → 0
ws variable → ∞ 400 µm 400 µm
λ 0 s 810 nm 810 nm 810 nm 810 nm
∆λs 0, 1, 10 nm → ∞ 10 nm → 0 10 nm
ϕs 10 ◦ 5, 10, 20 ◦ 5, 10, 20 ◦ 5, 10, 20 ◦
various values of the emission angle ϕs = ϕi, in degenerate type-i spdc configurations
described by the parameters listed in the second, third and fourth
columns of table 2.2.
Figure 2.7 (a) shows the case of finite spatial and temporal filters. The
purity of the signal photon is always smaller than one, increases with the emission
angle, and has a maximum for a given value of the pump beam waist. For
a very narrow band frequency filter with a ws = wi = 400 µm spatial filter,
figure 2.7 (b) shows how the correlation between the photons is minimal for
small pump beams. The emission angle for this particular crystal length is
irrelevant. Finally, figure 2.7 (c) considers a frequency filter ∆λs = ∆λi = 10
nm with infinitely narrow spatial filters. In this case, maximal purity appears
for each emission angle at a particular value of the pump beam waist.
Conclusion
Two photons with two degrees of freedom compose the two-photon state generated
in spdc. The correlations between all four elements affect the state of
single photons or two-photon states with one degree of freedom. Using the pu-
3mm
5º
10º
20º
27