Spatial Characterization Of Two-Photon States - GAP-Optique

5. Spatial correlations in Raman transitions
Schmidt number
40
20
1
-180º
0º 180º
lenght spatial filter
2 mm
1 mm
400 m
200 m
7
4
1
-180º
0º 180º
100 m
200 m
500 m
angle
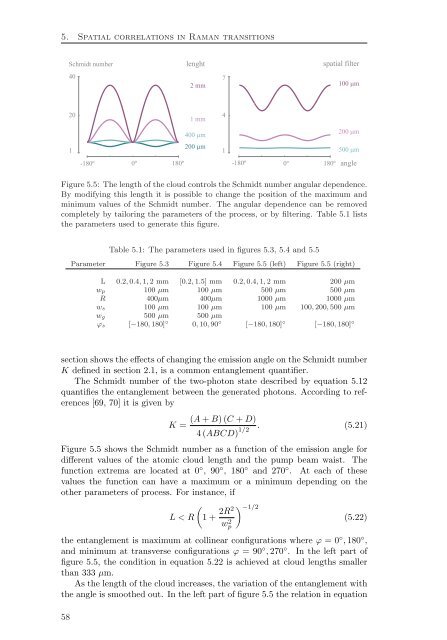
Figure 5.5: The length of the cloud controls the Schmidt number angular dependence.
By modifying this length it is possible to change the position of the maximum and
minimum values of the Schmidt number. The angular dependence can be removed
completely by tailoring the parameters of the process, or by filtering. Table 5.1 lists
the parameters used to generate this figure.
Table 5.1: The parameters used in figures 5.3, 5.4 and 5.5
Parameter Figure 5.3 Figure 5.4 Figure 5.5 (left) Figure 5.5 (right)
L 0.2, 0.4, 1, 2 mm [0.2, 1.5] mm 0.2, 0.4, 1, 2 mm 200 µm
wp 100 µm 100 µm 500 µm 500 µm
R 400µm 400µm 1000 µm 1000 µm
ws 100 µm 100 µm 100 µm 100, 200, 500 µm
wg 500 µm 500 µm
ϕs [−180, 180] ◦ 0, 10, 90 ◦ [−180, 180] ◦ [−180, 180] ◦
section shows the effects of changing the emission angle on the Schmidt number
K defined in section 2.1, is a common entanglement quantifier.
The Schmidt number of the two-photon state described by equation 5.12
quantifies the entanglement between the generated photons. According to references
[69, 70] it is given by
(A + B) (C + D)
K =
4 (ABCD) 1/2
. (5.21)
Figure 5.5 shows the Schmidt number as a function of the emission angle for
different values of the atomic cloud length and the pump beam waist. The
function extrema are located at 0 ◦ , 90 ◦ , 180 ◦ and 270 ◦ . At each of these
values the function can have a maximum or a minimum depending on the
other parameters of process. For instance, if
L < R
1 + 2R2
w2 −1/2
p
(5.22)
the entanglement is maximum at collinear configurations where ϕ = 0 ◦ , 180 ◦ ,
and minimum at transverse configurations ϕ = 90 ◦ , 270 ◦ . In the left part of
figure 5.5, the condition in equation 5.22 is achieved at cloud lengths smaller
than 333 µm.
As the length of the cloud increases, the variation of the entanglement with
the angle is smoothed out. In the left part of figure 5.5 the relation in equation
58