Signal Analysis Research (SAR) Group - RNet - Ryerson University

Recommendations

Info

Proceedings - 19th International Conference - IEEE/EMBS Oct. 30 - Nov. 2, 1997 Chicago, IL. USA The MP method represents a signal z(t) as: where and a, are the expansion coefficients. The scale factor s, is used to control the width of the envelope of grn(t), and the parameter p, controls the temporal placement. -& is a normalizing factor, which keeps the norm of gyn(t) equal to 1. The parameters fn and 4, are the frequency and phase of the exponential function, respectively. In our application, the envelope function is a Gaussian function, i.e., g(t) = 2'14 exp(--Kt2); the TF atoms are then called Gabor functions. In practice, the algorithm works as follows: First, the signal is projected on to a Gabor function dictionary. The projection decomposes the signal into two parts: 4t) = (",gro)g-Yo(t) + R14% (3) where (2, gyo) denotes the inner product (projection) of z(t) with the first TF atom gro(t). The second term R'z(t) is the residual vector after approximating z(t) in the direction of gyo(t). This process is continued by projecting the residue on to the dictionary, and after M iterations M-1 42) = (R"z,g,,)g,,(t) + R'4% (4) n=O with Roz(t) = ~ (2). There are two ways of stopping the iterative process: one is to use a pre-specified limiting number A4 of TF atoms, and the other is to verify the energy of the residue RMz(t). A very high value of M and a zero value for the residual energy will decompose the signal completely at the expense of increased compu- tational complexity. In this work, M was chosen to be 1000 atoms, the residual energy limit was set to be zero, and only coherent structures were extracted (i.e., components determined to be noise by the MP algorithm were rejected). 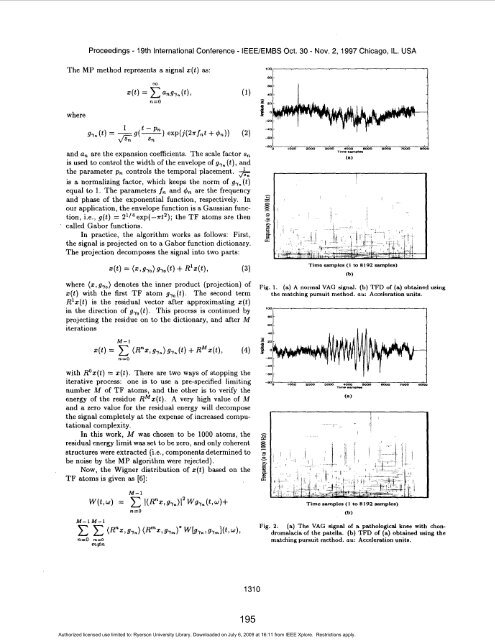Now, the Wigner distribution of t(t) based on the TF atoms is given as [6]: M-1 W(t,w) = I(Rnz,g,n)12 Wgyn(t,u)+ n=O - i P o -20 -40 Time samples (1 to 8 I92 samples) @) Fig. 1. (a) A normal VAG signal. (b) TFD of (a) obtained using the matching pursuit method. au: Acceleration units. Time samples ( I to R 192 samples) (b) M-1 M-1 Fig. 2. (a) The VAG signal of a pathological knee with chon- (R"z,grn) (Rmwrm)* ~bYn,gYml(t>4, dromalacia of the patella. (b) TFD of (a) obtained using the n=O m=o matching pursuit method. au: Acceleration units. m#n 1310 195 Authorized licensed use limited to: Ryerson University Library. Downloaded on July 6, 2009 at 16:11 from IEEE Xplore. Restrictions apply.
Proceedings - 19th International Conference - IEEE/EMBS Oct. 30 - Nov. 2, 1997 Chicago, IL. USA where Wgr,(t,w) is the Wigner transform of the Gaus- sian window function. The double sum corresponds to the cross-terms of the Wigner distribution, and should be removed in order to obtain an interference-free energy distribution of z(t) in the TF plane. Thus only the first term is retained, and the interference-free TFD is given by M-1 W’(t,4 = I(Rn~lSrn)IZwgrn(tlw). (5) n=O Figs.l(b) and 2(b) show the TFDs of the normal VAG signal in fig.l(a) and the abnormal VAG signal in fig.2(a). The TFD of the normal signal was computed using 392 TF atoms, and the abnormal signal’s TFD was computed using 441 TF atoms. The TFDs obtained are of very high resolution, and with synthetic signals of known TF dynamics, the TFDs based on the MP algorithm showed very good localization in both time and frequency. The bright spots in the TFD figures correspond to the TF atoms; the brightness increases with energy. In the illustration, the TFD of the abnormal signal shows more high-frequency activity than the TFD of the normal signal. However, this need not be always true (especially in the case of normal noisy knees), and mere visual interpretation of the TFDs will not help in discriminating pathological knees from normal knees. In order to differentiate the signals, features of diagnostic value need to be extracted from the TF plane. C. Time-Frequency Signal Features As the TFD obtained using the TF atoms is an interference-free distribution and is always positive, features derived from the TF plane will posses a high de- gree of accuracy as compared to features obtained with Cohen’s class TF transforms. The features used in the present work were computed as marginal calculations of the TFDs. The four TF features of relevance derived from the TFDs of VAG signals were: Instantaneous energy (IE): As the TFDs were obtained using TF atoms that were coherent with the signal structure and the signal components that were determined to be noise by the MP algorithm were rejected, the IE obtained as afunction of time will have a high signal-to-@se ratio. The IE was computed as the mean of W (t,w) along each time slice, which gives a measure of energy variation with time. Sig- nals generated by pathological knees will be highly time-variant (i.e., they are highly nonstationary) because of the differences in cartilage roughness and nonuniformity. Thus the IE of an abnormal signal is expected to show large variations with time. Instantaneous energy spread (IES): IES measures the spread of energy over frequency for each time slice. This was computed as the standard deviation 131 1 of W’(t,w) along each time slice. This is a good measure if the signal is multicomponent in nature. Abnormal VAG signals generated as a result of fric- tion between rough cartilage surfaces may have more components because of the nonuniformity of the surfaces, and a high signal energy spread is expected around the IE. Instantaneous mean frequency (IMF): IMF was computed as the first moment along each time slice: IMF measures the frequency dynamics of the signal. The movement of the knee during signal acqui- sition may cause some linear or nonlinear frequency modulation of the signal, with the modulation in- dex depending on the state of lubrication, stiffness, and roughness of the cartilage surfaces. Pathologi- cal knees have less lubricated and rougher cartilage surfaces than normal knees, and hence the IMF of pathological knees will be different from that of normal knees. Instantaneous mean frequency spread (IMFS): IMFS is given by the second central moment along each time slice: IMFS gives the spread of frequency about the mean frequency for each time instant. The spread of frequency at a time instant arises as a result of amplitude modulation. Amplitude modulation is pos- sible in VAG signals, and may be dependent on the quality and intensity of sound produced due to joint vibration. IMFS could be an excellent feature in identifying noisy knees, The four featires derived above are dependent on the functional state of the cartilage surfaces in the knee joint, and are expected to be suitable for discriminating pathological knees from normal knges. D. Pattern Classification The features discussed in previous section are time dependent. This could be easily observed in the wave- forms shown in fig.3, which were derived from the TFD shown in fig.2(b). In order to facilitate a global deci- sion on the signal, the mean and variance of the features were calculated. Therefore, a given VAG signal will have eight parameters. The classification of knees as normal or pathological was achieved using a statistical pattern clas- sifier based on discriminant analysis of the parameters [7]. The database was randomly split into two (almost) equal parts. The features of signals in one part of the database 196 Authorized licensed use limited to: Ryerson University Library. Downloaded on July 6, 2009 at 16:11 from IEEE Xplore. Restrictions apply.
Page 1 and 2:
Signal Analysis Research (SAR) Grou
Page 3 and 4:
2006.05 Support Vector Machines Bas
Page 5 and 6:
2001.05 Instantaneous Mean Frequenc
Page 7 and 8:
Class A Class B TWFB Mapping Discri
Page 9 and 10:
as an added advantage of this appro
Page 11 and 12:
Combining Vocal Source and MFCC Fea
Page 13 and 14:
probability distribution for calcul
Page 15 and 16:
Proceedings of the 29th Annual Inte
Page 17 and 18:
Fig. 1. Typical images of the small
Page 19 and 20:
This full text paper was peer revie
Page 21 and 22:
Frequency 1 0.9 0.8 0.7 0.6 0.5 0.4
Page 23 and 24:
Frequency TABLE I RESULTS WITH LINE
Page 25 and 26:
Emotion Recognition Using Novel Spe
Page 27 and 28:
points [1, 2, 3] (Fig. 2). SVM is b
Page 29 and 30:
A WATERMARKING METHOD FOR SPEECH SI
Page 31 and 32:
In order to exploit the masking eff
Page 33 and 34:
Chirp-based image watermarking as e
Page 35 and 36:
3.2.2 Discrete Polynomial Phase Tra
Page 37 and 38:
2006 International Joint Conference
Page 39 and 40:
Fig 2 Two-dimensional mapping (Left
Page 41 and 42:
p3 Feature Extraction u Database +
Page 43 and 44:
1424403677/06/$20.00 ©2006 I
Page 45 and 46:
= − = K ≤
Page 47 and 48:
DISCRETE POLYNOMIAL TRANSFORM FOR D
Page 49 and 50:
3.2. Watermark detection Fig.2 show
Page 51 and 52:
IMPROVING POSITION ESTIMATES FROM A
Page 53 and 54:
_ . r W-. n r We tried two ways of
Page 55 and 56:
Acknowledgements This work of Ryers
Page 57 and 58:
ing two consecutive keys. Another c
Page 59 and 60:
Table 1. Experimental Results for F
Page 61 and 62:
D as { gγ γ ∈ Γ, g = 1} = γ ,
Page 63 and 64:
frequency parameters issued from th
Page 65 and 66:
necessity of prediction, controllin
Page 67 and 68:
4. Experimental Results The objecti
Page 69 and 70:
Page 71 and 72:
Page 73:
Proceedings of the 2005 IEEE Engine
Page 78 and 79:
the whole spectrum but on non-overl
Page 80 and 81:
Identification Rate 1 0.9 0.8 0.7 0
Page 82 and 83:
signals. On some occasions, when us
Page 84 and 85:
For our first test, we recorded two
Page 86 and 87:
Frequency bands F4 F3 F2 F1 ME5 s1
Page 88 and 89:
as F1, F2, F3 and F4 as shown in Fi
Page 90 and 91:
Figure. 1. Motion Vector magnitudes
Page 92 and 93:
All the above descriptor were quant
Page 94 and 95:
2. METHODOLOGY 2.1. Local Discrimin
Page 96 and 97:
. each group, the posterior probabi
Page 98 and 99:
A NOVEL ROBUST IMAGE WATERMARKING U
Page 100 and 101:
where n is the distortion component
Page 102 and 103:
A Novel Way of Lossless Compression
Page 104 and 105:
111. IMPLEMENTATION As we have pres
Page 106 and 107:
CONTENT BASED AUDIO CLASSIFICATION
Page 108 and 109:
Entropy 4.5 4 3.5 3 2.5 2 1.5 1 0.5
Page 110 and 111:
MODIFIED LOCAL DISCRIMINANT BASES A
Page 112 and 113:
Tree Decomposition (0,0) (1,0) (1,1
Page 114 and 115:
RADIO OVER MULTIMODE FIBER FOR WIRE
Page 116 and 117:
3. COMPARISON OF MULTIMODE FIBER AN
Page 118 and 119:
SUB-DICTIONARY SELECTION USING LOCA
Page 120 and 121:
0 : SI 92 r3 54 =-ax Tirnep"idfh :
Page 122 and 123:
Proceedings of the 25h Annual Inter
Page 124 and 125:
estimated noise generated as the ou
Page 126 and 127:
ROBUST AUDIO WATERMARKING USING A C
Page 128 and 129:
where 0 is the angle of the ray pat
Page 130 and 131:
TIME-FREQUENCY FILTERING OF INTERFE
Page 132 and 133:
3. INTERFERENCE DETECTION. nouen AN
Page 134 and 135:
A GENERAL PERCEPTUAL TOOL FOR EVALU
Page 136 and 137:
Fig. 2. Snapshot of the GUI used fo
Page 138 and 139:
Non-Stationary Noise Cancellation i
Page 140 and 141:
signal and noise spectra overlap, f
Page 142 and 143:
Fig. 4: Output of the Comb filter.
Page 144 and 145:
Indoor infrared transmission suffer
Page 146 and 147:
The inverse wavelet transform is de
Page 148 and 149:
The simulations has been done using
Page 150 and 151: Figure 6: The original Gaussian noi
Page 152 and 153: 147 Authorized licensed use limited
Page 170 and 171: Figure 2: Block diagram of the FBB
Page 172 and 173: Figure 4: Benign mammogram before F
Page 174 and 175: . Table 1: Compression ratios of be
Page 176 and 177: Most Cohen’s class TFD derived fr
Page 178 and 179: the desired frequency marginal m(w)
Page 180 and 181: constructing an adaptive TFD and ex
Page 182 and 183: Proceedings of the 22"d Annual EMBS
Page 184 and 185: are: Proceedings of the 22"d Annual
Page 186 and 187: may be written as M-1 = (z,grn)gm,
Page 188 and 189: e 1 os 07- Ohzo5- 04- 09- 02- 01- O
Page 190 and 191: using the denoised signals. As an i
Page 192 and 193: signals are: 1) model-based TFD, 2)
Page 194 and 195: compared to that in the MP dictiona
Page 196 and 197: fied. In addition to being positive
Page 198 and 199: 08 [3] S. Peleg and B. Friedlander.
Page 202 and 203: Proceedings - 19th International Co
Page 204 and 205: the x and y axes correspond to the
Page 206 and 207: Fig. 5. Results with synthetic sign
Page 208 and 209: the users and is explained in next
Page 210 and 211: ,-t 1 2 J 4 5 e 7 e e 10 SNR (I" de
Page 212 and 213: 'il! (c) (a) Weakea User 2nd Strong
Page 214 and 215: 18th Annual International Conferenc
Page 216 and 217: quisition board and Lab Windows (Na
Page 218 and 219: Table 1: Comparison of different cl
Page 220: K. Umapathy and S. Krishnan, Low bi
show all

Signal Analysis Research (SAR) Group - RNet - Ryerson University

Create successful ePaper yourself

Delete template?

Save as template?