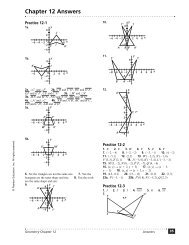
Chapter 12 Sequences; Induction; the Binomial Theorem

Chapter 12: Sequences; Induction; the Binomial Theorem
98. Yes, a sequence can be both arithmetic and
geometric. For example, the constant sequence
3,3,3,3,..... can be viewed as an arithmetic
sequence with a 1 = 3 and d = 0. Alternatively,
the same sequence can be viewed as a geometric
sequence with a 1 = 3 and r = 1.
99 – 100. Answers will vary.
101. Answers will vary. Both increase (or decrease)
exponentially, but the domain of a geometric
sequence is the set of natural numbers while the
domain of an exponential function is the set of
all real numbers.
Section 12.4
1. I: n = 1: 2⋅ 1= 2 and1(1 + 1) = 2
II: If 2+ 4+ 6+ + 2 k = k( k+
1) , then
2+ 4+ 6+ + 2k+ 2( k+
1)
= ( 2+ 4+ 6+ + 2k)
+ 2( k+
1)
= kk ( + 1) + 2( k+
1)
2
= k + 3k
+ 2
= ( k + 1)( k + 2)
= ( k+ 1) ⎡⎣( k+ 1)
+ 1⎤⎦
Conditions I and II are satisfied; the statement is
true.
2. I: n = 1: 4⋅1− 3= 1and1(2⋅1− 1) = 1
II: If 1+ 5+ 9 + + (4k − 3) = k(2k−1)
, then
1+ 5+ 9 + + (4k− 3) + [4( k+ 1) −3]
= [ 1+ 5+ 9 + + (4k− 3) ] + 4k+ 4−3
= k(2k− 1) + 4k
+ 1
2
= 2k − k+ 4k+
1
2
= 2k
+ 3k+
1
= ( k+ 1)(2k
+ 1)
= ( k+ 1) ⎡⎣2( k + 1)
−1⎤⎦
Conditions I and II are satisfied; the statement is
true.
3. I:
1
n = 1: 1+ 2 = 3and ⋅ 1(1 + 5) = 3
2
1
II: If 3+ 4+ 5 + + ( k+ 2) = ⋅ k( k+
5) , then
2
3+ 4+ 5 + + ( k+ 2) + [( k+ 1) + 2]
= [ 3+ 4+ 5 + + ( k+ 2) ] + ( k+
3)
1
= ⋅ kk ( + 5) + ( k+
3)
2
1 2 5
= k + k + k+
3
2 2
1 2 7
= k + k + 3
2 2
1 2
= ⋅ ( k + 7k+
6)
2
= 1 ⋅ ( k+ 1)( k + 6)
2
= 1 ⋅ ( k+ 1)[( k + 1) + 5]
2
Conditions I and II are satisfied; the statement is
true.
4. I: n = 1: 2⋅ 1+ 1= 3and1(1 + 2) = 3
II: If 3+ 5+ 7 + + (2k+ 1) = k( k+
2) , then
3 + 5 + 7 + + (2k+ 1) + [2( k+ 1) + 1]
= [ 3+ 5+ 7 + + (2k+ 1) ] + (2k+
3)
= kk ( + 2) + (2k+
3)
2
= k + 2k+ 2k+
3
2
= k + 4k+
3
= ( k + 1)( k + 3)
= ( k + 1)[( k+ 1) + 2]
Conditions I and II are satisfied; the statement is
true.
1262
© 2009 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all copyright laws as they currently
exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.