Chapter One: Vector Analysis The use of vectors and vector analysis ...

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Chapter One: Vector Analysis
The use of vectors and vector analysis can greatly simplify the mathematics used in
expressing and manipulating the laws and theorems of electric and magnetic fields.
Scalars and Vectors:
Scalar is a quantity that has only magnitude, such as: time, distance, temperature, entropy,
energy, mass, electric potential ………
The vector is a quantity that has both magnitude and direction, such as: velocity, force,
displacement, electric and magnetic field intensity …………
Vector Operations
1‐ Addition of two vectors:
B
‐B
A
A+B
A+B
A
A‐B
A
B
2‐ Multiplication by a scalar:
3‐ Dot product of two vectors (Scalar Product):
∙
A
B
∙ ∙
∙ ∙ ∙
∙
⟹ ∙ 0
1

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Example:
Let , calculate the dot product of with itself:
∙ ∙ ∙ ∙ ∙ ∙
2
This is the law of cosine.
4‐ Cross product of two vectors (Vector Product):
where is a unit vector, pointing perpendicular to the plane of and . (the direction
pointed by right‐hand rule).
Right‐hand rule: Let your finger point in the direction of the first vector and curl around (via
the smaller angle) toward the second; then your thumb indicates the direction of .
0
Vector Algebra:
Let , , and be unit vectors parallel to the , , and respectively.
An arbitrary vector can be expanded in term of these basis vectors:
The numbers , , and are called components of .
∙ ∙
∙
∙ ∙ ∙ 1
2

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙ ∙ ∙ 0
∙
||
∙ ; ∙ ; ∙
In the case of cross product:
Therefore:
0
This cumbersome expression can be written as a determinant:
Where is perpendicular to both and .
Prove of dot product rule:
,
,
3

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙ ∙
cos cos
cos cos sin sin
∴ ∙ cos
Prove of cross product rule:
2 2
2
2 2 2
2
2 2
∙ cos 1cos sin
∴ sin
Vector Directions:
The position vector or radius vector of point , , is defined as the directed distance
from the origin 0,0,0 to point , , as:
The distance vector is the displacement from one point to another, such as, , , to
, , and is represented mathematically as:
Therefore, the position vector is a special case of displacement vector.
4

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Example:
Find the angle between the face diagonals of a cube.
Let:
z
(0,0,1)
x
(1,0,0)
(0,1,0)
y
1 0 1
0 1 1
∙ 0011
|| √2 ; || √2
∙ ⟹ ∙
1 2
⟹ 60 °
Problem:
Find the angle between the body diagonals of a cube.
Let:
z
(0,0,1)
x
(1,0,0)
(0,1,0)
y
5

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
1 1 1
1 1 1
∙ 1111
|| √3 ; || √3
∙ ⟹ ∙
1 3
⟹ 70.5288 °
Problem:
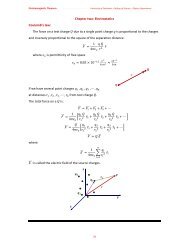
Use the cross product to find the components of the vector perpendicular to the plane
shown in Fig.
z
3
x
1
2
y
Let:
1 2 0
1 0 3
1 2 0 6 3 2
1 0 3
6 3 2 7
Triple Products:
Since the cross product of two vectors is itself a vector, it can be dotted or crossed with a
third vector to form a triple product.
1‐ Scalar triple product: ∙
Geometrically ∙ is the volume of the parallelepiped generated by , ,
6

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙ ∙ ∙
∙
2‐ Vector triple product:
∙ ∙
∙ ∙ ∙ ∙
∙ ∙
Prove: ∙ ∙
∙ ∙
∴ Left hand = right hand.
Problem:
Prove that: 0
Since; ∙ ∙
∙ ∙ ∙ ∙ ∙ ∙ 0
Problem:
Under what conditions dose
7

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
We have
∙ ∙ ∙ ∙
∙ ∙
If this is zero; then either is parallel to (including the case in which they point in
opposite directions, or one is zero), or else ∙ ∙ 0 in which case is
perpendicular to and (including the case 0).
Concluding: either:
1‐ is parallel to , or
2‐ is perpendicular to and .
Position Displacement:
The location of a point in three dimensions can be described by listing its Cartesian
coordinates , , . The vector to that point form the origin is called the position vector;
Its magnitude:
The unit vector pointing radially outword, is
||
̂
||
z
, ,
y
x
The infinitesimal displacement vector, from , , to , , is:
The infinitesimal surface of Cartesian Coordinate is:
8

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Vector Transformation:
Suppose, the , , system is rotated by angle , relative to , , , about the
common ′.
cos
sin
z'
z
While;
y'
′
cos cos cos cos sin sin cos sin
sin sin sin cos cos sin sin cos
In matrix notation;
′
′
More generally, for rotation about an arbitrary axis in three dimensions:
′
′
′
Tenser of rank 2
In general an n th ‐rank tensor has 3 n components.
y
9

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Gradient:
Suppose, we have a function of three variables, say, the temperature ,, in a room.
A theorem on partial derivative state that the derivative of can be calculated from:
This tells us how changes when alter all three variables by the infinitesimal amount ,
, ; Above equation in a dot products
Where;
Is the gradient of .
∙ ∙
is a vector quantity.
The gradient points in the direction of maximum increase of the function .
The magnitude gives the slop (rate of increase) along this maximal direction.
If gradient vanish 0 at , , . this is, then, a stationary point of the function
, , . It could be a maximum or a minimum points.
is called "Del" operator.
Del is not a vector, it is without specific meaning until we provide it with a function to act
upon.
Example:
Find the gradient of
2
2
2
|| ̂
10

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
The Divergence:
Del operator act on a vector function , via the dot product.
∙V ∙
The result is scalar.
∙V
The divergence is measure, how much the vector spreads out.
Positive Divergence
Zero Divergence
Positive Divergence
Example:
Calculate the divergence of the following vector functions:
a/
∙ 1113
b/ 2 2
∙ 2 2 0222
Problem:
Compute the divergence of ̂
∙
∙ / / /
11

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙
/ 2
/
2
/
2 /
∙ 3 3
∙3
3 0
/
/
/
The Curl:
Del operator can act on a vector function , via the crosss product:
The curl measure, how much the vector curl around the point in question.
Two
figures have a substantial curl.
Example:
Calculate
the curl of functions:
2
0
0 0

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Problem:
Calculate the curls of functions:
3 2
6 2 3
3 2
2 3
2 3
2 3
2 2
0
2 2
Product Rules:
The calculation of ordinary derivatives is facilitated by a number of general rules, such as:
The sum rule:
The rule for multiplying by a constant:
The product rule:
And, the quotient rule:
There are six product rules for Del operator:
Two for gradients:
13

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙ ∙ ∙
Two for divergences:
∙ ∙ ∙
∙ ∙ ∙
and, two for curls:
∙ ∙ ∙ ∙
The proofs of these rules wanted.
The proofs come straight from the product rule for ordinary derivatives.
It is also possible to formulate three quotients rule:
∙
∙ ∙
The proofs of these rules wanted.
Problems:
Prove product rules:
Problems:
Prove product rules:
∙ ∙ ∙
14

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙
∙
∙
∙
∙
∙ ∙ ∙
Problems:
Prove product rules:
∙ ∙ ∙
∙
∙
∙
∙
∙
∙
∙ ∙ ∙
Problems:
Prove product rules:
15

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Problem: Compute ̂ ∙̂ where ̂ is the position unit vector.
̂
||
Let’s just do the component:
1
̂ ∙̂
̂ ∙̂
1
1
1
2
1
2 1
2
̂ ∙̂
1
1
̂ ∙̂
1 1
0
Same goes for the other components: Hence; ̂ ∙̂ 0
16

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Problem:
Let 2 3 ,
3 2
Check product rules:
1‐ ∙ ∙ ∙
2‐ ∙ ∙ ∙
3‐ ∙ ∙ ∙ ∙
Proof of (1):
2 36 9 2 6
3 2 0
∙ 6 9 2 6
∙ 6 9 0 15
3 2 3 2 0
∴B ∙ 0
0 2 3 0 2 3
5
∴A ∙ 15
∴ ∙ ∙ 015 15
∴ ∙ ∙ ∙
Second Derivatives:
The gradient, the divergence, and curl are the only first derivative we can make with ; by
applying twice we can construct five species of second derivatives,
The gradient is a vector, so we can take the divergence and curl of it:
1‐ Divergence of gradient: ∙
2‐ Curl of gradient:
The divergence ∙ is a scalar, all we can do is take its gradient:
3‐ Gradient of divergence: ∙
17

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
The curl is a vector, so we can take its divergence and curl:
4‐ Divergence of curl: ∙
5‐ Curl of Curl:
Let’s consider them one at a time:
1)
∙ ∙
∙
This object, which we write is called the Laplacian of .
Note that the Laplacian of a scalar is a scalar. Occasionally, we shall speak of the Laplacian
of a vector, .
2)
The curl of a gradient is always zero:
0
This is an important fact, which we shall use repeatedly.
3)
∙ for some reason seldom occurs in physical applications.
Notice that ∙ is not the same as the Laplace of vector:
∙ ∙
4)
The Divergence of curl ∙ , like the curl of gradient, is always zero:
∙ 0
5)
From definition of
∙
We could go through a similar ritual to work out third derivative, but fortunately second
derivative suffice for practically all physical applications.
18

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Problem:
Calculate the Laplacian of the following functions:
a) 234
b) sin sin sin
c) sin 4 cos 3
d) 3 2
a))
b))
2 ;
0 ⟹ 2
sin sin sin ⟹ 3 sin sin sin 3
c))
d))
25 ;
16 ;
9 ⟹ 0
2 ;
0 ⟹ 2
0 ;
6 ⟹ 6
0 ⟹ 0
2 6
Problem:
Prove that the divergence of a curl is always zero.
∙
∙
∙
By equality of cross‐derivative:
∙ 0
19

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Problem:
Prove that the curl of gradient is always zero.
By equality of cross‐derivative:
0
20

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Integral Calculus:
1‐ Line integrals (Path):
A line integral is an expression of
the form,
∙
where is a vector function,
is the infinitesimal displacement vector.
And the integral is to
be carried out along a prescribed path from point to point .
If the path in question forms a closed loop (that is if ), I shall put a circle on the integral
sign:
∙
Example of line integrals is the work done by
a force :
∙
Ordinarily, the value of a line integral depends critically on the particular path taken from
to .
But if the
line integral is independent of the path; a force
that has this property is called
Conservative.
Example:
Calculate
the line integral of the function 2 1 from the point
1 ,1
, 0 to the point 2 , 2 , 0 along the paths 1 & 2 in Fig. What is
∮ ∙
for the loop
that goes from to along 1 and returns to along 2?

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙ 21 ∙
Path 1 consists of two paths:
(i) along the horizontal segment
∙ 21
0 ; ; 1
∙ ⟹ ∙
(ii) along the vertical segment
0 ; ; 2
∙ 21 41 ⟹ ∙ 4 1
∴ Path 1
∙
11011
1
10
On path 2:
; ; 0 ;
∙ 2 1 3 2
∙
3 2 2 1 10
∙ 11101
2‐ Surface integrals (Flux):
A surface integral is an expression of the form:
∙
where is again some vector function, is an infinitesimal path of area, which direction
perpendicular to the surface.
22

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
If the surface is closed, in which case I shall again put a circle on the integral signs:
∙
Example:
Calculate
the surface
integral of
2 2 3
over five sides
(excluding the bottom) of the cubical box ( side 2 ) in Fig.
(i)
2 ;
⟹
∙ 2 4
(ii)
∙ 4
16
0 ;
⟹
∙ 2
0
∙ 0
(iii)
2
;
⟹
∙
2
∙
2 12
(iv)
0
;
⟹
∙ 2
∙
2 12
(v)
2 ;
⟹
∙ 3

Electromagnetic Theorem (Dr. Omed G
Department
Ghareb Abdullah) University of Sulaimani –College of Science – Physics D
∙
4
Evidently
the total flux is:
∙ 160
12122 420
3‐ Volume integrals:
A volume
integral is an expression of the form:
where is a scalar function and is an infinitesimal volume element:
in Cartesian coordinates:
Occasionally we shall encounter volume integrals of vector functions:
because the unit vectors are constants, they
come outside the integral.
Example:
Calculate
the volume
integral of
over the prism in Fig.
1
2
3 3 0 2 2
3
4 1 0 9 1 12 3 8

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Example:
Calculate the volume integral of over the volume in Fig.
z
(0,0,1)
y
(0,2,0)
x
(3,0,0)
3 2
3
3 2 0
3 0 1
20 03 06
2 3 6
Using equation of normal on the surface , and the point 3 , 0 , 0
the surface equation can be found from the equation:
0
∴ 2 3 3 0 6 0 0
2 3 6 6 0
⟹ 3 3
To find the relation between and ; we use the two points
⟹
, ⟹ 2 , 0
, ⟹ 0 , 1
2
0 02
10
⟹
2 2 ⟹ 2 2
2
2
2
25

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
9 3 3
9 18
9 9 9
312
18 12
3
3 12 18 12 3
33
2
918
9 9 9
1 70
3
2
The Fundamental Theorem for Gradients:
Suppose we have a scalar function of three variables , , , going from to along
the path , the total change in well be:
Notes:
Line integrals ordinary depend on the path taken from to .
But the right side of above equation makes no referencee to the path
– only to the end
points.
∙

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Evidently, gradient have the special property
that their line integral are path independent.
Corollary(1):
∙ is independent of path taken from to .
Corollary(2):
∮ ∙
0 since the beginning and end points are identical, and hence 0.
Example:
Let
, and take point to be the origin 0 , 0 , 0 and the
point 2 , 1 , 0. Check
the fundamental theorem for gradients.
Althoughh the integral is independent of path, we must pick specific path in order to
evaluate it.
Let’s go out along the
(step ) and then up (step );
The fundamental theorem of Gradient state:
0 ;
T y 2
∙
2
⟹
2
(i)
∙ 2
0 ;
0
⟹
T
∙ 0
T
∙ 0

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
(ii)
2
; 0
⟹ T∙ 2
4
T∙ 4 2
1 0 2
We have 20 2
If we tack
the path (iii):
⟹
⟹ T∙
2
T∙
2
The Fundamental Theorem for Divergences:
The fundamental theorem for divergences state that:
∙ V ∙
This theorem has at least three special names:
Gauss’s theorem , Green’s theorem , or, simply, the Divergence theorem.
It say that the integral of a derivative (in this
case the divergence) over a region (in this case
a volume) is equal to
the value of the function at the boundary (in this case the surface) that
bounds the volume.
Example:
Check the
divergencee theorem using the function:
2
2
and the unit cube situated at the
origin.
Solution:

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
The fundamental theorem for divergences state that:
(i)
∙
V ∙
∙ 2
∙ 2 2
⟹
∴ ∙ 2
1 ⟹ 1 1
(ii)
(iii)
(iv)
(v)
(vi)
So the total flux is:
∙
∙
∙
∙
∙
2
∙
2 1
0 0
∙ 1
3 1
3 4
3 1
3 102
29

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Problem:
Test the divergence theorem for the function:
2 3
Take as your volume the cube shown in Fig., with sides of length (2).
Solution:
The fundamental theorem for divergences state that:
∙
∙
∙
∙
∙
∙ V ∙
∙ 23
2 4 6
∙ 8 16
∙ 4 16
2 0
∙163248
2
3
23
2
46 2 0

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Numbering the surfaces as in Fig:
(i)
; 2 ; ∙ 2
(ii)
∙
2 8
; 0 ; ∙ 0
∙ 0
(iii)
; 2 ; ∙ 4
(iv)
∙
4 16
; 0 ; ∙ 0
∙ 0
(v)
; 2 ; ∙ 6
(vi)
∙
6 24
; 0 ; ∙ 0
∙ 0
31

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
So the total flux is:
∙ 8 162448
The Fundamental Theorem for Curls:
The fundamental theorem of Curls, which goes by the special name of Stokes’ theorem state
that:
∙ V
As always, the integral of a derivative (here, the curl) over a region (here, a patch of surface)
is equal to value of the function at the boundary (here, the perimeter of the patch).
∙
If your finger point in
the direction of the line integral, then your thumb fixed the direction
of .
Corollary(1):
∙ depends only on the boundary line, not on the particular surface
used.
Corollary(2):
∮
∙ 0 for any closed surface.
Example:
Suppose
2 3 4
Check Stokes’ theorem for the square surface in Fig.

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
The Stokes’ theorem state that:
∙ V
∙
∵ 0
4 2 2
⟹ ∙ 4 2
∙ 4
3
⟹ ∙ 4
Breaking the line integral into four segments:
(i)
0
; 0 ; ∙ 3
(ii)
0
; 1 ; ∙ 4
(iii)
0
(iv)
; 1 ; ∙ 3
0 ; 0 ; ∙ 0
⟹
⟹
⟹
⟹
∙ 3 1
∙ 4 4 3
∙
3 1
∙ 0
0

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics D
So:
V ∙ 1
4
3 10
4
3
Problem:
Test Stokes’ theorem
for the function:
2 3
Using the
triangular shaded arm of Fig.
The Stokes’ theorem state that:
∙ V ∙
0 2 03 0
2 3
2 3
⟹ ∙ 2
∙ 2
∙ 2
0
∙ 2
∙ 44
∙ 4 2
Department

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙ 88
Meanwhile;
∙ 2 3
There are three segments:
(i)
(ii)
0 ; 0 ; : 0 ⟶ 2
∙ 0 ⟹ ∙ 0
0 ; 2 ; 0 ; ; : 2 ⟶ 0
∙ 2 22 ⟹ ∙ 22
∙ 4
∙ 2
∙ 8 2
3 8 8
3
(iii)
So:
0 ; 0 ; : 2 ⟶ 0
∙ 0 ⟹ ∙ 0
V ∙ 8
3
35

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Orthogonal Coordinate Systems:
The most standardd orthogonal coordinate
systems that are commonly used are:
(1) Cartesian (or Rectangular) Coordinate System , ,
(2) Spherical Coordinate System
, ,
(3) Cylindrical Coordinate System
, ,
Spherical Polar Coordinates:
The spherical plot coordinates
, , of a point are definedd in Fig;
∶ 0 ⟶ ∞
∶ 0 ⟶
∶ 0 ⟶ 2
: is the distance from the origin (the magnitude of the
position vector).
: the angle down from the z‐axis, is called
the polar angle.
: the angle around
from the x‐axis, is the azimuthal angle.
Their relation to Cartesian coordinates , , can read from the
figure.
sin cos
sin sin
cos
Any vector can be expressed as:
, & are the
radial, polar & azimuthal components of .
, & are unit vectors, pointing in the direction of
increase of
the corresponding
coordinates.
In terms of the Cartesian unit vectors:
sin
cos sin sin cos
coscos cos sin sin
sin cos

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of S
Check: ∙ ∙ ∙ 1
∙ ∙ ∙ 0
; ;
∙
sin cos sin sin cos
cos cos cos sin sin
sin cos 0
An infinitesimal displacement in the direction is:
An infinitesimal element of length in the direction is:
An infinitesimal element of length in the direction is:
sin
Thus, the
general infinitesimal displacement
is:
sin
The infinitesimal volume element , in spherical coordinates, is:
sin
For surface elements
:
1‐ If is constant:
sin
Science – Physics Department

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics D
2‐ If is constant:
sin
3‐ If is constant:
In general:
sin sin
Here, are
the vector derivative in
spherical coordinates:
Gradient:
T ∂ T
∂r 1 ∂T
∂θ 1 ∂T
s in ∂φ
Divergence:
1 ∂
∙V
∂r 1 ∂
sin ∂θ sin 1 ∂
sin ∂φ
Curl:
V 1
sin
∂ ∂θ sin
∂
∂φ 1 1 ∂
∂ sin ∂φ ∂r
1 ∂ ∂r ∂
∂θ
Laplacian:
1 ∂ ∂T
T ∂r ∂r 1 ∂
sin ∂θ sin ∂T
∂θ 1 ∂ T
sin
∂φ Department

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Problem:
Compute the Gradient and Laplacian of the function
Solution:
cossincos
T ∂T
∂r 1
∂T
∂θ
1
sin
∂T
∂φ
T cos sin cos sin cos cos 1
sin sin sin
cos sin cos sin cos cos sin
T ∙
T 1 ∂ ∂T
∂r ∂r 1
sin
T 1 ∂
1
∂r cos sin cos
sin
1
sin
∂
sin sin
∂φ
1 ∂ ∂r cos sin cos 1
sin
1
sin
∂
sin
∂φ
∂ ∂T
sin
∂θ ∂θ 1
sin
∂ T
∂φ
∂
sin sin cos cos
∂θ
∂
sin sin cos cos
∂θ
1 1
2 cos sin cos
sin 2 sin cos cos cossin cos
1
sin cos
1
sin 2sincos2sin cos2 sincoscos cossin cos
cos
1
sin sin cos cos cos 0
Problem:
Check the divergence theorem for the function , using spherical volume of radius
, centered at the origin.
Divergence theorem state:
∙
V ∙
39

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
∙V 1 ∂
∂r 1
sin
∙V 1 ∂
∂r 1
sin
∂
∂θ sin
1
sin
∂
∂θ 0 1
sin
∙V 1 4 4
∂
∂φ
∂
∂φ 0
∙ 4 sin
4 sin
4
22 4
4
V ∙ ∙ sin
At surface of sphere .
sin
4π
Problem:
Check the divergence theorem for the function , using as your volume the
sphere of radius , centered at the origin.
Divergence theorem state:
∙
∙V 1 ∂
∂r 1
sin
∙V 1 ∂
∂r 1 1
sin
V ∙
∂
∂θ sin
∙V 0
∙ 0
1
sin
∂
∂θ 0 1
sin
∂
∂φ
∂
∂φ 0
V ∙ 1 ∙ sin
40

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
sin
4π
They don’t agree!!!!! !!
Problem:
Compute
the divergence of the function:
cos sin
sin cos
Check the
divergencee theorem for this function, using as
your volume the inverted
hemispherical bowl of radius , resting on the plane
and centered at the origin.
Divergence theorem state:
∙ V ∙
1 ∂
∙V
∂r 1 ∂
sin ∂θ sin 1 ∂
sin ∂φ
1 ∂
1 ∂
∂r cos sin ∂θ si
1 ∂
in sin
sin ∂φ sin cos
1 1
1
3 cos 2 sincos
sin sin sin sin
3 cos 2 cos sin
5 cossin
∙ 5 cos sin sin
/
5 cos sin sin
/
3 5 coscos 2 0 sin

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
/
3 2 5 cos sin
sin
10
3 2
/
5
3
We have two surfaces:
1) The hemisphere:
sin
; : 0 → 2 ;
: 0 → /2
V ∙ cos sin
/
sincos
π
2) The flat bottom: sin
/2 ; : 0 → 2 ; : 0 →
V ∙ sin sin
The total:
2π
3
V ∙ π
2π
3 5 3 π
Problem:
Test the Gradient theorem for the function:
cos sincos
Using the
path shown in Figure, from 0 , 0 , 0 to 0 , 0 , 2.

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Solution:
The Gradient theorem state:
∙
T ∂T
∂r 1
∂T
∂θ
1
sin
∂T
∂φ
T cos sin cos sin cos cos 1
sin sin sin
cos sin cos sin cos cos sin
Segment (1):
; 0 ; : 0 →2
; T∙ cos sin cos 01
T∙
2
Segment (2):
; 2 ; : 0 →
sin 2 ; T∙ sin2 2sin
/
T∙ 2sin
2cos| / 2
Segment (3):
2 ;
; : →0
2 ; T∙ sin cos cos 2 2sin
Total:
Mean while;
T∙ 2sin
/
T∙
2cos| /
2222
2
0 ; 2 ; 2
43

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Cylindrical Coordinates:
The cylindrical coordinates , , of a point are defined in Fig.
: is the
distance from the z‐axis.
∶
∶
0 ⟶ ∞
0 ⟶ 2
∶
∞ ⟶ ∞
Their relation to Cartesian coordinates , , is:
cos
sin
Any vector can be expressed as:
, & are unit vectors, pointing in the direction of
increase of
the corresponding
coordinates. In terms
of the Cartesian unit vectors:
cos
sin
sin cos
∙
cos
sin
0
sin
cos
0
0
0
1

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
The infinitesimal displacements in cylindrical coordinates are:
Thus, the general infinitesimal displacement is:
The infinitesimal volume element , in cylindrical coordinates, is:
The infinitesimal surface elements , in cylindrical coordinates, is:
The vector derivatives in cylindrical coordinates are:
Gradient:
Divergence:
Curl:
Laplacian:
V 1
∙V 1
T ∂T
∂ 1
∂
∂ 1
∂T
∂φ ∂T
∂z
∂
∂φ ∂ ∂z
∂
∂ ∂
∂z ∂
∂z ∂
∂ 1 ∂
∂ ∂
∂
T 1
∂
∂
∂T
∂ 1 ∂ T
∂φ ∂ T
∂z
Problem:
a) Fide the divergence of the function:
V 2sin φ sinφcosφ 3z
45

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
b) Test the divergence theorem for this function, using the quarter‐cylinder (radius 2, height
5) shown in Fig.
c) Find the curl of V.
a))
∙V 1
∙V 1
∂
∂
∂
∂ 1
2
sin φ
1
∂
∂φ ∂ ∂z
∂
sinφcos
∂φ φ ∂ ∂z 3
∙ V V 1
2 2sin φ
1 cos
φsin φ 3
∙V 4 2 sin φ cos φ sin φ3
∙V 7sin φcos φ
b)) Divergence theorem state:
∙V 8
∙ V ∙
∙ 8
Mean while, the surface integral has five parts:
8
/
82
5 40
2
Top: 5 ;
Bottom: 0
V ∙ 3 15
V ∙ 15
15
;
/

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
V ∙ 3 0
V ∙ 0
Back:
;
V ∙ sincos 0
V ∙ 0
Left: 0 ;
V ∙ sincos 0
Front: 2 ;
V ∙ 0
V ∙ 2sin φ 4 2sin φ
So,
/
V ∙ 4 2sin φ
4 5 25
4
/
V ∙ 15 25 40
2sin φ 2 sin φ 2| /
1cos2
/
/
sin2
/
4
/
/2 sin 0 sin0
c))
V 1
V 1
∂
∂ ∂
∂z ∂
∂z ∂
∂ 1 ∂
∂ ∂
∂
∂
∂ 3z ∂ ∂z sinφcosφ ∂ ∂z 2sin φ ∂
∂ 3z
1 ∂
∂ sinφcosφ ∂
∂ 2sin φ
V 00 00 1 2 sin φ cos φ 2 sin φ cos φ 0
47

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Example: If
10
Determine the flux of out of the entire surface of a cylinder 1 ; 0 1.
z
(i)
(iii)
Solution1: There are three surfaces:
Flux through the surface (i):
x
(ii)
y
Φ E ∙ 10 ∙
Flux through the surface (ii):
10
1 ; : 0 → 1 ; : 0 → 2
Φ 10 10 π
Φ E ∙ 10 ∙
Flux through the surface (iii):
10
0 ; : 0 → 1 ; : 0 → 2
Φ 10 10 π
Φ E ∙ 10 ∙
10
1 ; : 0 → 1 ; : 0 → 2
Φ 10
Flux through all surface of a cylinder:
10
2 1 2π 10π 1
ΦE ∙ 10π 10π 10π 1 0
48

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Solution2:
Using the divergence theorem:
∙E 1
∙E 1
ΦE ∙
∂
∂ 1
∂
∂ 10 1
∙
∂
∂φ ∂ ∂z
∂
∂φ 0 ∂ ∂z 10
∙E 1 2 10 2 10 0
Φ ∙ 0
Classification of Vector Field:
A vector field is uniquely characterized by its divergence and curl. All vector fields can be
classified in terms of their vanishing or non‐vanishing divergence or curl as follows:
(1) A vector field A is said to be Solenoid (or divergence less) if ( ∙ 0 ) [such field has
neither source nor sink of flux]. Examples of such fields are (magnetic field, conduction
current density under steady state condition). The Solenoid field can always be
expressed in terms of another vector such as :
∙ 0 ⇒ A ⇒ ∙ 0
(2) A vector field is said to be irrotational (or conservative) if 0, examples of such
fields are [Electrostatic field and gravitational field]. Thus, an irrotational field can
always be expressed in terms of a gradient of scalar field , that is:
0 ⇒ A ⇒ 0
(3) The field is said to be divergence if ∙ 0.
(4) The field is said to be Rotational (or non‐conservative) if 0.
(5) When V0, the field is said to be harmonic.
(6) When the field is independent on position the field is said to be uniform field.
(7) When the field is independent on time the field is said to be constant field.
49

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Transformation between Coordinate Systems
The position of a given point in space is invariant with respect to the choice of coordinate
system. That is, its location is the same irrespective of which specific coordinate system is
used to represent it. The same is true for vectors. The relation between the variables
( x,
y,
z)
‐Cartesian ( ,
,
z)
Cylindrical and ( r,
, )
in Spherical coordinates will be
established to transform any one of the three system into vectors expressed in any of the
other two.
1. Cartesian to Cylindrical Transformation:
Point P in the figure has Cartesian coordinate ( x,
y,
z)
and cylindrical coordinate ( ,
,
z)
. Both systems share the coordinate (z), and the relation between the other two pairs of
coordinates can be obtained as follows:
ρ
ρ
â z
â
â
sin
cos
x cos
y sin
z z
x
tan
2
1
y
y
x
2
aˆ
aˆ
aˆ
x
x
x
aˆ
aˆ
aˆ
z
cos
sin
0
aˆ
aˆ
aˆ
y
y
y
aˆ
aˆ
aˆ
z
sin
cos
0
aˆ
aˆ
aˆ
z
z
z
aˆ
aˆ
aˆ
z
0
0
1
Therefore, when we have a vector in Cartesian coordinate given by:
A A aˆ
A aˆ
A aˆ
x
x
y
y
z
z
50

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Then this vector is transformed to cylindrical coordinate as follows:
A ˆ ˆ ˆ ˆ ˆ ( ˆ ˆ
A a
A
x
( ax
a
) A
y
( a
y
a
) A
z
az
a
)
A aˆ
( ˆ ˆ ) ( ˆ ˆ ) ( ˆ ˆ
A
A
x
ax
a
A
y
a
y
a
A
z
az
a
)
A A aˆ
A ( aˆ
aˆ
) A ( aˆ
aˆ
) A ( aˆ
aˆ
)
z
z
x
x
z
y
y
z
In matrix notation, we can write the transformation of vector (A) from A , A , A ) to
( A , A
, A
z
) as:
z
z
z
(
x y z
A
A
A
z
aˆ
a
ˆ
a
ˆ
x
x
x
aˆ
aˆ
aˆ
z
aˆ
aˆ
y
aˆ
y
y
aˆ
aˆ
aˆ
z
aˆ
z
aˆ
z
aˆ
z
aˆ
aˆ
aˆ
z
A
A
A
x
y
z
A
A
A
z
cos
sin
0
sin
cos
0
0
0
1
A
A
A
x
y
z
While when we have a vector ( A ) in cylindrical coordinate given by:
A( ,
,
z)
A aˆ
A aˆ
A ˆ , then this vector can be transformed to Cartesian
coordinate as:
A ˆ
x
A a
x
A
A ˆ
y
A a
y
A
A A aˆ
A
z
z
( aˆ
( aˆ
( aˆ
z
a z
aˆ
( ˆ
x
) A
a
aˆ
) ( ˆ
y
A
a
aˆ
) A ( aˆ
z
aˆ
x
) A
aˆ
y
) A
aˆ
) A
z
z
z
( aˆ
z
( aˆ
( aˆ
These equations in matrix notation can be written as:
z
z
z
aˆ
aˆ
aˆ
x
z
y
)
)
)
A
A
A
x
y
z
aˆ
a
ˆ
a
ˆ
aˆ
aˆ
aˆ
x
y
z
aˆ
aˆ
aˆ
aˆ
aˆ
aˆ
x
y
z
aˆ
aˆ
z
z
aˆ
z
aˆ
aˆ
aˆ
x
y
z
A
A
A
z
A
A
A
x
y
z
cos
sin
0
sin
cos
0
0
0
1
A
A
A
z
2. Cartesian to Spherical Transformation:
Point P in the figure has Cartesian coordinate ( x,
y,
z)
and spherical coordinate ( r , , )
.
The relation between the coordinates can be obtained as follows:
51

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
â r
â
â
r sin
r sin cos
r sin sin
x r sin
cos
y r sin
sin
z r cos
r
x
tan
2
1
cos
y
1
y
x
z
r
2
z
2
aˆ
aˆ
aˆ
x
x
x
aˆ
r
aˆ
aˆ
sin
cos
cos
cos
sin
aˆ
aˆ
aˆ
y
y
y
aˆ
aˆ
aˆ
r
sin
sin
cos
sin
cos
aˆ
aˆ
aˆ
z
z
z
aˆ
aˆ
aˆ
r
cos
sin
0
Therefore, when we have a vector in Cartesian coordinate given by:
A A aˆ
A aˆ
A aˆ
x
x
y
y
z
z
Then this vector is transformed to spherical coordinate as follows:
A
A
A
r
A aˆ
A aˆ
A aˆ
r
A
A
A
x
x
x
( aˆ
x
( aˆ
( aˆ
x
x
aˆ
( ˆ
r
) A
y
a
y
aˆ
) ( ˆ
A
y
a
aˆ
) A ( aˆ
y
y
y
aˆ
( ˆ ˆ
r
) A
z
az
ar
)
aˆ
) ( ˆ ˆ
A
z
az
a
)
aˆ
) A ( aˆ
aˆ
)
In matrix notation, we can write the transformation of vector (A) from A , A , A ) to
( A r
, A , A
) as:
z
z
(
x y z
Ar
aˆ
x
aˆ
A
a
ˆx
aˆ
A
a
ˆx
aˆ
r
aˆ
aˆ
y
y
aˆ
y
aˆ
r
aˆ
aˆ
aˆ
aˆ
z
z
z
r
aˆ
aˆ
aˆ
aˆ
A
A
A
x
y
z
A
A
A
r
sin
cos
cos
cos
sin
sin
sin
cos
sin
cos
cos
sin
0
A
A
A
x
y
z
52

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
While when we have
a vector ( A ) in spherical coordinate given by:
A ( r , ,
) A ˆ
A
coordinate as:
A
x
A aˆ
x
A
A
y
A aˆ
y
A
A A aˆ
A
z
z
r
a r
r
r
r
( a
ˆ
(
a
ˆ
(
a
ˆ
r
r
r
â
A
These equations in matrix notation can be written as:
aˆ
x
) A
aˆ
y
) A
aˆ
) A
z
aâ , then this
vector can be transformed to Cartesian
( aˆ
ˆ
ax
) A ( ˆ ˆ
a
ax
)
( aˆ
aˆ
y
)
A ( ˆ ˆ
a
a
y
)
( aˆ
aˆ
) A ( aˆ
aˆ
)
z
z
A
A
A
aˆ
r
aˆ
a
ˆr
aˆ
a
ˆr
aˆ
x
y
z
x
y
z
aˆ
a
ˆ
aˆ
aˆ
aˆ
aˆ
x
y
z
aˆ
aˆ
x
aˆ
aˆ
y
aˆ
aˆ
z
A
A
A r
A
x
A
y
A
z
sin
cos
sin
sin
cos
cos
cos
cos
sin
sin
sin
cos
0
A
A
A r
3. Cylindrical to Spherical Transformation:
Point P in the figure has cylindrical coordinate ( ,
,
z)
and spherical coordinate ( r , ,
) .
The relation between
the coordinates can be
obtained as follows:
x
r sin
cos
y
r sin
sin
z
r cos
and
and
and
x cos
y
sin
z
z
r sin
z r cos
r
x
tan
tan
2
2
1
1
z
y
y
x
z
2
2

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
aˆ
aˆ
aˆ
aˆ
aˆ
aˆ
r
sin
cos
0
aˆ
aˆ
aˆ
aˆ
aˆ
aˆ
r
0
0
1
aˆ
aˆ
aˆ
z
z
z
aˆ
aˆ
aˆ
r
cos
sin
0
Therefore, when we have a vector in cylindrical coordinate given by:
A A aˆ
A aˆ
A ˆ
z
a z
Then this vector is transformed to spherical coordinate as follows:
A ˆ ˆ ˆ ˆ ˆ ˆ ˆ
r
A ar
A
( a
ar
) A
( a
ar
) A
z
( az
ar
)
A ˆ ( ˆ ˆ ) ( ˆ ˆ ) ( ˆ ˆ
A a
A
a
a
A
a
a
A
z
az
a
)
A A aˆ
A ( aˆ
aˆ
) A ( aˆ
aˆ
) A ( aˆ
aˆ
)
In matrix notation, we can write the transformation of vector (A) from A , A
, A ) to
( , A , A
) as:
A r
z
z
(
z
A
A
A
r
aˆ
a
ˆ
a
ˆ
aˆ
r
aˆ
aˆ
aˆ
aˆ
aˆ
aˆ
r
aˆ
aˆ
aˆ
aˆ
z
z
z
r
aˆ
aˆ
aˆ
aˆ
A
A
A
z
A
A
A
r
sin
cos
0
0
0
1
cos
sin
0
A
A
A
z
While when we have a vector ( A ) in spherical coordinate given by:
A( r,
,
)
A aˆ
A aˆ
A aˆ
, then this vector can be transformed to cylindrical
r
r
coordinate as:
A ˆ ˆ ˆ ( ˆ ˆ ˆ ˆ
A a
A
r
( ar
a
) A
a
a
) A
( a
a
)
A aˆ
( ˆ ˆ ) ( ˆ ˆ ) ( ˆ ˆ
A
A
r
ar
a
A
a
a
A
a
a
)
A A aˆ
A ( aˆ
aˆ
) A ( aˆ
aˆ
) A ( aˆ
aˆ
)
z
z
r
r
z
These equations in matrix notation can be written as:
z
z
A
A
A
z
aˆ
r
aˆ
a
ˆr
aˆ
a
ˆr
aˆ
z
aˆ
aˆ
aˆ
aˆ
aˆ
aˆ
z
aˆ
aˆ
aˆ
aˆ
aˆ
aˆ
z
A
A
A
r
A
A
A
z
sin
0
cos
cos
o
sin
0
1
0
A
A
A
r
Example(1):
Let A cos
aˆ
z
2
sin
aˆ
z
, then :
a. Transform A into Cartesian coordinate and calculate its magnitude at point (3,‐4,0).
b. Transform A into spherical coordinate and calculate its magnitude at point (3,‐4,0).
54

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Solution:
(a). since the vector is in cylindrical coordinate, and we have the following matrix to
convert it to Cartesian coordinate:
A
A
A
x
y
z
cos
sin
0
sin
cos
0
0
0
1
A
A
A
z
A
A
A
x
y
z
cos
sin
0
sin
cos
0
0
0
1
cos
0
2
z sin
A
A
A
x
y
z
cos
2
sin
cos
0 0
0
0 z
A
x
0 0
2
sin
2
5cos
( 53.13)
1.8
at point (3,‐4,0) : tan
A
y
z 0
Therefore, the vector in Cartesian coordinate is:
2
2
A cos aˆ
cos
sin
aˆ
z sin
aˆ
x
y
x
2
1
y
y
x
2
tan
9 16
5
1
5sin( 53.13)cos(
53.13)
2.3
z
A 1.8
aˆ
x
4
53.13
3
2.3aˆ
y
0
A
z
5
0
sin( 53.13)
0
(b). since the vector is in cylindrical coordinate, and we have the following matrix to
convert it to spherical coordinate:
A
A
A
r
sin
cos
0
0
0
1
cos
sin
0
A
A
A
z
A
A
A
r
sin
cos
0
0
0
1
cos
sin
0
cos
0
2
z sin
The spherical point of ( 3, ‐4, 0) is given by :
A
r
sin
cos
z
2
cos
sin
A
r
x
2
cos
tan
y
1
1
z
r
y
x
cos
cos
z
2
2
z
cos
tan
2
1
1
sin
sin
9 16
0 5
0
90
5
4
53.13
3
A
0
0 0 0
A r
A
5sin 90 cos( 53.13)
5
0
cos90 sin( 53.13)
5cos90
cos( 53.13)
5
0
sin 90 sin( 53.13)
A
0
A (
sin
cos
z
A 3aˆ
0 aˆ
0 aˆ
z
2
cos
sin)
aˆ
A 3aˆ
3
0
( cos
cos
z
2
sin
sin)
aˆ
0 aˆ
z
55

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Example(2):
(a). find the length of each of the curves: 3,
,
4 2
z cons tan t.
(b). Calculate the area of the surfaces area defined by: z 1, 1 3 , 0
4
(c). determine the volume of the region defined by: 1 r 3 ,
2
,
2 3 6 2
Solution:
(a).
dl d
dl
/ 2
d
3 ( / 2
/ 4)
4
/ 4
3
l unit
length
(b)
ds d
d
3 / 4
1 4
3 /
2
ds
d
d
( ) ( )
4
2
1 0
4
1
0
S
unit
of
area
(c).
dv r
2
sin
dr d
d
dv
3 2
/ 3 / 2
1 / 2
/ 6
3
r
sin
dr d
d
3
1
v (27 1)
(cos
/ 2 cos 2
/ 3) ( / 2 / 6)
3
1
13
v (26) (0
0.5) (
) v unit of
3
3
9
r
2
volume
3
1
( cos
)
2
/ 3
/ 2
( )
/ 2
/ 6
Example(3):
Find the gradient of the following scalar functions:
a. U 4 x z
2 3 y z , b. 2 ( z 2 2
W 1)
cos
, c. V r cos cos
.
(a).
U (
x
aˆ
x
y
aˆ
y
z
aˆ
)(4xz
z
2
3yz)
4 z
2
aˆ
x
3z aˆ
y
(8xz
3y)
aˆ
z
(b).
W ( aˆ
1
aˆ
z
aˆ
)(2 (
z
1) cos)
2( z
1) cos
aˆ
2 ( z
1) sin
aˆ
4 z cos
ˆ
2
2
2
z
a z
56

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
(c).
V (
r
aˆ
r
1
r
aˆ
r
1
sin
aˆ
)( r
2
cos
cos)
2 r cos
cos
aˆ
r
r sin
cos
aˆ
r cot
sin
aˆ
Example(4):
For the vector field
E 10 e aˆ
3 z aˆ
, verify the divergence theorem for the cylindrical
z
region enclosed by : 2 m , z 0 and z 4 m ?
The divergence theorem
mathematically states that:
E ds ( E)
dv
S
Z=4 m
Z
=2 m
There are three closed
surfaces bounded by the
defined region, they are:
Z=0
Y
Therefore the right hand side of the equation of divergence theorem is:
E ds E ds E ds E ds
S
S1
S 2
S 2
S 2
S
E ds
E ds
E ds
S1
2
2
0 0
2
2
0 0
2
2
0 0
(10
(10
(10
E ds
43.3
S 2
aˆ
E ds 0
48 43.3
4.7
e
e
e
aˆ
aˆ
S 3
3 z aˆ
)
d
d
( aˆ
)
z
3 z aˆ
) d
d
aˆ
z
3 z aˆ
) dz d
aˆ
z
z
z
2
2
0 0
2
2
0 0
2
2
0 0
1 2
3 z d
d
3 z (2
) 3
0 2 2
0
2
1 2
3 z d
d
3 z (2
) 3
4
2
2
48
2
10
e
2
dz d
10
e
2
z (2
) 10
e
2
4
4 (2
)
While the Left hand side is:
1 (
E
) 1 E
E
z
E
z
1
2
E (20 e 10e
) 3
2
1 (
10e
) 1 (0) (
3z)
z
57

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
v
(
E
) dv
first term
2
4 2
0 0 0
2
4 2
0 0 0
second
term
third term
(20 e
20 e
2
4 2
0 0 0
2
4 2
0 0 0
10 e
10
e
2
dd
dz 80
e
3 d
d
dz
d
d
dz 160
e
d
2
d
2
3 d
d
dz 24
d
24
2
2
0
2
0
2
0
by ( u dv)
by ( u dv)
2
0
48
Example(5):
Verify Stoke’s theorem for a vector field
, in the segment of cylindrical surface
defined by 2 , 60 90 , and 0 3 .
The mathematical representation of Stokes’s theorem is given by:
L
A dl
L
A ds
The line integral around a closed path defined by these bounded region is as follows:
L
b
a
c
b
d
c
a
d
B dl
B dl
B dl
B dl
B dl
b
a
B dl
B aˆ
z
z
z
z
z
B aˆ
z
B aˆ
z
B aˆ
z
c
b
d
aˆ
dz aˆ
B dl
z
0
d
( aˆ
) 0
3
0
dz ( aˆ
)
z
d
c
B dl
cos
cos90
dz z
2
3
0
a
d
B dl
0
cos
cos60
dz z
2
3
0
3
0
3
4
ρ
The left hand side of the Stokes’s theorem is :
A
s
ds
58

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
aˆ
aˆ
1
B
0 0
1
B
2
cos
aˆ
aˆ
z
z
cos
sin
aˆ
1
aˆ
sin
( 0) aˆ
cos
(0 ) aˆ
2
z
(0 0)
Hence,
s
s
s
1
( B)
ds cos
aˆ
2
s
1
( B)
ds (cos)
3 1
( B)
ds (0 )
2 2
sin
aˆ
s
dz d
aˆ
/ 2 3
/ 3 0
sin
dz d
2
/ 2 3
1
( z)
(cos
/ 2 cos
/ 3) (3 0)
/ 3
0 2
3
( B)
ds
4
It is clearly seen that the left and right hand side has the same value, which indicates the
validity of the Stokes’s theorem.
Example (6):
transform into spherical coordinate and find its magnitude at point 3, 4, 0.
Solution:
∙ ∙ ∙ ∙
∙ ∙ ∙ ∙
∙ ∙ ∙ ∙
∙ ∙ ∙
∙ ∙ ∙
∙ ∙ ∙
0
0
0 1 0
59

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
√9165
√25 5
0 5 90
4
3 53.13
5sin90 cos53.13 5 0 cos90 sin53.13
5cos90 cos53.13 5 0 sin 90 sin 53.13 .
3 0 0.018
Example(7):
Determine the flux of through the entire prism shown in Fig.
Solution:
z
c
The equation of surface (abc) is:
1
1 ,3 ,6
6 2 6 ⟹ 662
x
a
b
y
The equation of line (ab) is:
⟹
3 3 ⟹ 3 3
To find flux through the entire prism we can use divergence theorem:
∮ . ∙ ∙ 3
. 3
. 3 6 6 2
. 3 63 3 63 3 2
3 3
2
60

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
. 27
. 27 1 3 1 4 1 5 7.65
Example(8):
Show that if the scalar function , is harmonic at point √3, ,0 .
Solution:
∂
∂θ
H 1 ∂
r ∂r r sin θ e 1
H 1 ∂ ∂H
r r
∂r ∂r 1
r sinθ
sinθ
∂H
∂θ 1
∂ H
r sin θ ∂φ
∂
r sinθ ∂θ sinθ2 sin θ cosθ e
H sin θ
r r e 2r e 2 e
r sinθ sin θ 2sinθ cos θ
H sin θ
r
e r2 2 e
r 2 cos θ sin θ
At point √3, ,0, H0 ⟹ is not harmonic.
1
r sin θ 0
Example (9):
Display whether the field vector is solenoid, conservative or none of them?
Solution:
(1). In order to show that the field is solenoid, it must be satisfy: ∙A 0
∙A 1 r ∂ ∂r r A 1
rsinθ
Therefore the field is not solenoid:
∂
∂θ sin θ A 1 ∂A
rsinθ ∂φ
∙A 1 r ∂ ∂r r 1 r r 3 0
(2). In order to show that the field is conservative, it must be satisfy: A 0
1
1
0 0
1
00 00 00 0
Therefore the field is conservative.
61

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
More example on Chapter One
Example(10):
Given vectors
(a). A B
(b). 3 A
B
A aˆ
3aˆ
and B 5aˆ
x
z
x
2aˆ
y
6aˆ
z
, then determine the following:
(c). the component of A along aˆ
y
(d). the unit vector parallel to 3A
B
Solution:
(a). A
B ( aˆ
3aˆ
) (5aˆ
2aˆ
6aˆ
) 6aˆ
2 aˆ
3 aˆ
A
B
36 4 9 7unit
x
z
x
y
z
x
y
z
(b). 3A
B
(3aˆ
9aˆ
) (5aˆ
2aˆ
6aˆ
) 2aˆ
2aˆ
15aˆ
x
z
x
y
z
x
y
z
(c). the scalar component of
A along aˆ
is given by: A Aaˆ
( aˆ
3aˆ
) aˆ
0
y
y
y
x
z
y
(d). 3A
B
(3aˆ
9aˆ
) (5aˆ
2aˆ
6aˆ
) 8aˆ
2aˆ
3aˆ
, then the unit vector
x
z
x
y
z
x
y
z
parallel to this vector is calculated as:
3A
B
a ˆ3 AB
3A
B
8aˆ
x
2 aˆ
y
3aˆ
64 4 9
z
8aˆ
x
2 aˆ
y
77
6 aˆ
z
Example(11):
Given points P( 1, 3,5) , Q(2,4,6)
and R(0,3,8)
, then find the following:
(a). the position vectors of P and R
(b). the distance vector r
QP
(c). the distance between Q and R
Solution:
62

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
OP (1 0) aˆ
x
( 3
0) aˆ
y
(5 0) aˆ
z
aˆ
(a).
OR (0 0) aˆ
(3 0) aˆ
(8 0) aˆ
3aˆ
x
y
z
x
y
3aˆ
8aˆ
z
y
5aˆ
z
(b). r
QP
( 1
2) aˆ
( 3
4) aˆ
(5 6) aˆ
aˆ
7 aˆ
aˆ
x
y
z
x
y
z
(c).
2
2
2
QR (0 2) (3 4) (8 6) 4 1
4 3unit
Example(12):
Derive the cosine formula
c
2
2 2
a b 2abcos
and the sine formula
sin A sin B sin C
using dot and cross product respectively.
a b c
b
C
Cosine formula:
c a
b
c c (
a b)
(
a b)
a
c
2
a
2
b
2
2
b
2
A
c
2a
b
2 2
2ab
cos c a b 2abcos
a
B
Sine formula:
1 1
a b b c
2 2
1
2
a bsin
c
1
2
1
c a
2
b c sin a
1
2
c a
sin b
dividing
the above equation
by
( a b c ) we get :
sin c
c
sin a
a
sin b
b
Example(13):
Let E 3aˆ
4aˆ
and F 4aˆ
10aˆ
5aˆ
, then find:
x
z
x
y
z
(a). the component of
E along
F
(b). A unit vector perpendicular to both
E and
F
Solution:
(a). the vector component of
E along F is given by:
63

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
E
F
E cos
aˆ
F
E F
F
( E aˆ
) aˆ
4 aˆ
ˆ ˆ ˆ ˆ ˆ
x
10
a
y
5 a
z
4 a
x
10
a
y
5 a
z
aˆ
F
16 100 25
141
4 aˆ
10 ˆ 5 ˆ
x
a
y
a
z
( E aˆ
) aˆ
(3aˆ
4 ˆ
F F
x
a
z
)
141
(12 20)
E (4 aˆ
10 ˆ 5 ˆ
F
x
a
y
a
z
)
141
aˆ
F
F
F
4 aˆ
x
10
aˆ
y
141
5 aˆ
z
The scalar component of E along F is given by:
E F
E
ˆ
F
E cos
E aF
F
4 aˆ
10
ˆ 5 ˆ
x
a
y
az
12 20
E aˆ
(3aˆ
4 ˆ
F
E
F
x
a
z
)
141 141
Example(14):
Three field quantities are given by: P aˆ
aˆ
,
Q 2aˆ
aˆ
2aˆ
,
2
x z
x y z
R 2aˆ
3aˆ
aˆ
,
x
y
z
determine the following:
(a). ( P Q)
( P Q)
P ( P Q)
Q
( P Q)
,
(b). Q ( R P)
(c). sin QR
(d). P ( Q R)
(e). A unit vector perpendicular to both Q and R
(f). The scalar and vector component of P along
Q
Solution:
( P Q)
( P Q)
P ( P Q)
Q
( P Q)
P P P Q Q
P Q
Q
0
Q P Q
P 0
2 P Q sinQP
(a). P 4 1
5 Q 4 1
4 3
1
Q P 4 2 2
QP
cos
72.65
P Q 3
5 3 5
sin 72.65 0.95
64

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
2 1
2
(b). Q ( R P)
2 3 1 2
(3 0) 1
(2 2) 2
(0 6) 6 4 12
14
2 0 1
(c).
sin
QR
Q R
aˆ
x
Q R
Q R 2
Q R
2
25 4 16
45
aˆ
y
aˆ
z
1
2
3 1
,
Q
aˆ
( 1
6) aˆ
(4 2) aˆ
( 6
2) 5aˆ
2aˆ
x
4 1
4 3
and
y
z
R 4 9 1
14
x
y
4aˆ
z
sin
QR
3
45
14
0.596
(d).
aˆ
x
aˆ
y
aˆ
z
P ( Q R)
2 0 1
aˆ
(0 2) aˆ
( 5
8) aˆ
(4 0) 2aˆ
3aˆ
4aˆ
5 2 4
x
y
z
x
y
z
(e).
aˆ
QR
Q R
Q R
5aˆ
x
2 aˆ
y
3 14
4 aˆ
z
(f). The scalar and vector component P along Q can be calculated as follows:
The scalar component of P along Q is equal to:
P Q
P
ˆ
Q
P cos
P aQ
Q
2 aˆ
ˆ 2 ˆ
x
a
y
a
z 4 2 2
P aˆ
(2
aˆ
ˆ
Q
x
a
z
)
3 3 3
The vector component of P along Q is given by:
65

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
P
Q
E cos
aˆ
F
P Q
Q
aˆ
Q
(
P aˆ
) aˆ
2aˆ
ˆ ˆ
x
a
y
2 az
aˆ
Q
3
2 aˆ
ˆ 2 ˆ 2 ˆ ˆ 2 ˆ
x
a
y
az
ax
a
y
a
( P aˆ
) ˆ (2 ˆ ˆ
Q
aQ
a
x
az
)
3 3
4 2
2
P (2aˆ
ˆ 2 ˆ ) (2 ˆ ˆ 2 ˆ
Q
x
a
y
a
z
ax
a
y
az
)
9
9
Q
Q
z
Example(15):
Find the distance between the following pairs of points:
a‐ P 1 (1,1,2) and P 2 (0,2,2)
b‐ P 1 (2, ,1) and P2
(4, ,0)
,
3
2
c‐ P
1( 3, , ) and P2
(4, , ) .
2
2
Solution:
(a).
2
2
2
P P (1 0) (2 2) (1 2) 2
1 2
unit
(b).
x
x
p
p1
p2
1
p
cos
2 cos60 1
cos
4 cos90 0
2
1
2
1
2
(1 0)
2
(1.73 4)
2
y
(1 0)
p1
y
2
sin
2sin 60 1.73
p2
1
sin
4sin 90 4
2
1
2.06 unit
2
z
p1
z
1
p2
0
(c).
x
x
p1
p2
p p
1
r sin
cos
3sin
cos90 0
r
2
1
2
1
sin
cos
4sin 90cos
4
2
1
2
(0 ( 4))
2
(0 0)
2
( 3
0)
2
y
p1
y
r sin
sin
2sin
sin 60 0
p2
1
r
2
sin
sin
4sin 90sin
0
16 9 5 unit
1
2
1
2
z
p1
r cos
3cos
3
z
1
p2
r
2
1
cos
4cos90 0
2
Example(16):
Convert the coordinates of the following points from Cartesian to cylindrical and spherical
coordinates : a‐ P 1 (1,2,0) , b‐ P 2 (0,0,3) and c‐ P 3 (1,1,2)
66

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Solution:
In general the Cartesian coordinates are related to cylindrical and spherical coordinates by
the following equations:
r
x
x
2
2
y
y
2
2
z
2
tan
1
tan
y
x
1
y
x
z z
cos
Therefore these points in cylindrical coordinates are given as follows:
1
z
r
x
(a).
P1
P1
1
x
2
P1
y
y
P1
2
P1
2
5
P1
and
tan
1
y
x
P1
P1
z
P1
0
tan
1
2
63
1
and
z
P1
0
P 1(
5,63 ,0)
x
P2
(b).
0
P2
x
2
P2
y
y
P2
2
P2
0
0
P2
and
tan
1
y
x
P2
P2
z
P2
3
tan
1
0
90
0
and
z
P2
3
P
2
(0,90
,3)
x
P3
(c).
1
P3
x
2
P3
y
P3
y
1
2
P3
2
and
P3
tan
1
z
y
x
P3
P3
P3
2
tan
1
1
45
1
and
z
P3
2
P 3(
2,45 ,2)
Also these points in spherical coordinates are given as follows:
(a).
x
r
P1
P1
1
x
2
P1
y
y
2
P1
P1
z
2
2
P1
5
and
tan
P1
1
y
x
z
P1
P1
P1
0
tan
1
2
63
1
and
P1
cos
1
0
90
5
P 1(
5,63 ,90
)
xP2
0
(b).
P2
x
2
P2
y
y
P2
2
P2
0
z
2
P2
3
and
P2
z
tan
P2
1
3
y
x
P2
P2
tan
1
0
90
0
and
P2
cos
1
3
0
3
P
2
(3,90
,0
)
67

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
(c).
x
P3
1
P3
x
2
P3
y
P3
y
1
2
P3
z
2
P3
6
and
P3
z
P3
tan
2
1
y
x
P3
P3
tan
1
1
45
1
and
P3
cos
1
2
35.26
6
P
3 (
6,45 ,35.26 )
Example(17):
Express vector
in Cartesian coordinates.
Solution:
0
1
But: ;
sin
cos
sin
cos
; tan
10
∙
10
∙
10
Example(18):
If ∅ evaluate ∮ . around the path shown in Figure:
Solution:
∙
∙
1‐ ∙
2| √3 1
68

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
2‐ ∙ 30
3‐ ∙
5|
4‐ ∙ 60
√
√3 1
∙ √3 1 21√3
4 5√3
2 5 2 21
4 27 √3 1
4
Example(19):
Show that the scalar field 10 is not harmonic.
Solution:
10
1
1
1
10 1
20
202
1
10 2 22 2 1
10 1 22
∎ T0 The function is not harmonic.
102 10
102
10
Example(20):
Obtain the spherical coordinates of 10 at the point 3, 2, 4.
Solution:
Giving vector is in Cartesian system say 10
∙ 10 ∙ 10sincos
∙ 10 ∙ 10coscos
∙ 10 ∙ 10sin
3 2 4 √29
tan tan 2 3 33.69
cos cos 4
√29 42.03
69

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
But, is negative and is positive hence must be between 90 and 180 , so add 180 to
:
33.69 180 146.31
10sin42.03 cos146.31
10cos42.03 cos146.31
10sin146.31
5.57 6.18 5.547
Example(21):
A particular vector field cos sin , is in the cylindrical system. Find the
flux due to this field over a close surface of the cylinder 4 , 01 , verify the
divergence theorem.
Solution:
z
(1)
(3)
(2)
y
Surface (1):
Surface (2):
Surface (3):
∙ cos sin ∙ 0
∙ cos sin ∙ 0
∙ cos sin ∙
cos
4 1cos2
sin 2
32
2 64
The divergence theorem state:
∙ ∙
∙ 1
1
x
1
cos 1
sin 0
70

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
3cos cos
∙ 3 cos cos
:
3 cos cos
cos cos
64 cos 4cos
64 cos 2 cos
64 cos 2cos
321cos2 2cos
sin 2
32 2sin 64
2
∙ ∙ & .
Example(22):
Given that calculate the circulation of around the closed path
shown in Figure.
Solution:
Line (1):
∙
0 , 0 ,
∙
∙
71

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Line (2):
Line (3):
Line (4):
∙
3 1 3
0 , 0 ,
∙ 0
∙ 0
1 , ,
∙
∙ 1
3 2 3
1 , ,
∙
∙
2
3 5 6
∙ 1 2 02 3 5 6 1 6
Example(23):
For an harmonic scalar function sin 4 cos 3. Find and .
Solution:
The curl of grad is always zero:
Since the function is harmonic:
∴ 0
∴ 0
Example(24):
transform into spherical coordinate and find its magnitude at point 3, 4, 0.
∙ ∙ ∙ ∙
∙ ∙ ∙ ∙
∙ ∙ ∙ ∙
∙ ∙ ∙
∙ ∙ ∙
∙ ∙ ∙
72

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
0
0
0 1 0
√9165
√25 5
0 5 90
4
3 53.13
5sin90 cos53.13 5 0 cos90 sin53.13
5cos90 cos53.13 5 0 sin 90 sin 53.13 .
3 0 0.018
Example(25):
Show that if the scalar function , is harmonic at point √3, ,0 .
∂
r sinθ ∂θ
H 1 ∂
r ∂r r sin θ e 1
H 1 ∂ ∂H
r r
∂r ∂r 1
∂H
sinθ
∂θ 1
∂
∂ H
r sin θ ∂φ
r sinθ ∂θ sinθ2 sin θ cosθ e
H sin θ
r r e 2r e 2 e
r sinθ sin θ2sinθ cos θ
H sin θ
r
e r2 2 e
r 2 cos θ sin θ
At point √3, ,0, H0 ⟹ is not harmonic.
1
r sin θ 0
Home Work:
Q 1 / Prove that: ( V A ) V
A AV
, where V is a scalar field and A is a vector field ?
73

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
Q 2 / prove that:
( V A)
V
A V
A , where V is a scalar field and A is a vector
field?
Q 3 / Show that:
Q 4 / Given vectors
2
2
( A B)
( A B)
( A B
A
aˆ
x
2aˆ
y
3aˆ
z
2
) .
, B 3aˆ
x
4aˆ
y
and
C 3aˆ
y
4aˆ
z
, find the
following:
a. A and aˆ
A
, b. the component of B along C , c.
AC
, d. A
C
,
e. A ( B C)
, f. A ( B C)
, g. aˆ x
B , h. ( A
aˆ
y
). aˆ
z
.
Q 5 / Express the unit vector directed toward the point ( 0,0, h ) from an arbitrary point in the
plane z 2
. Explain the result as h 2
?
x aˆ
ˆ
x
y a
y
Ans.
( h 2) aˆ
z
2 2
2
x y ( h 2)
Q 6 / Given A 4aˆ
10aˆ
and
B 2aˆ
3aˆ
, find the magnitude and vector
y
z
y
x
components of A on B ?
Q 7 / Find the angle between A 10aˆ
2aˆ
, and B 4aˆ
0.5aˆ
, using both dot and
cross product.
Q 8 / Given A aˆ
aˆ
x
y
,
B 2aˆ
z
and
z
y
C aˆ
x
3aˆ
y
y
, find both
A B C and ( A B)
C ? Ans. 4 , 8
âz
.
Q 9 / Given A ( y 1)
aˆ
2 x aˆ
, find the vector at point ( 2,2,1)
and its projection on vector
Q 10 / If
B
, where B 5aˆ
aˆ
2aˆ
?
x
x
x
y
F F x
aˆ
, what can be said about F if ;
1. F 0 every where ,
2. F 0 every where ,
y
z
z
3. F 0 and F 0 every where?
2
3
3
Q 11 / Given field A 3 x y z aˆ
x z aˆ
( x y 2 z)
aˆ
x
y
z
, it can be said that A is :
a. Harmonic, b. Divergenceless, c. Solenoid, d. Rotational, e. Conservative.
Q 12 / If a vector field A is solenoid, which of the following is true:
a. A dl 0 , b. A ds 0 , c. A 0 , d. A 2
0 , e. A 0 .
L
S
Q 13 / If ( r
) is the position vector of point (x,y,z) and r r , then prove that :
74

Electromagnetic Theorem
(Dr. Omed Ghareb Abdullah) University of Sulaimani –College of Science – Physics Department
aˆr
a. (ln r)
and b.
2 (ln r)
1
2
r
r
3 2 2
Q 14 / Let G x y z aˆ
, then calculate: a. G
, b. G
, c. G
, d.
G x
x
Q 15 / Evaluate
V , V
, and V
if :
Q 16 / If
2
a. V 3 x y x z , b. V z cos
, c. V 4r
2 cos sin
.
r x aˆ
x
y aˆ
y
z aˆ
z
is the position vector of point (x,y,z) and r r , then which of
r
the following is incorrect: a. r , b. r 1 , c.
2 ( r r
) 6
r
, d. r 0 .
Q 17 / Determine which of the following vector fields is harmonic, solenoid or conservative ;
2
2 2
a. A 2 x y aˆ
x
y aˆ
y
, b. B x aˆ
x
y aˆ
y
2 z aˆ
z
, c. C ( 3 ) aˆ
z aˆ
z
1
1
r
d. D aˆ
r
, e. E r ar
r
e ˆ
sin
cos
, f. F aˆ
aˆ
2 2
75